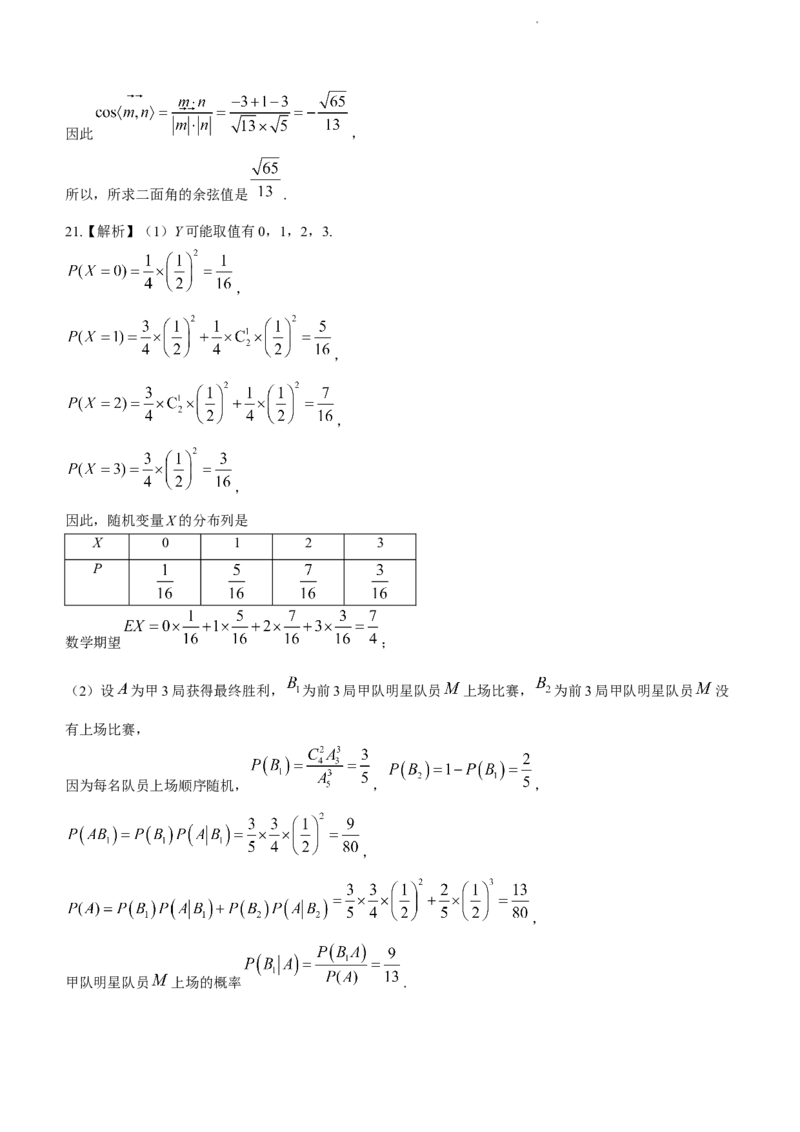文档内容
南昌市三校(一中、十中、铁一中)高三上学期第一次联考
数学试卷
试卷总分:150分 考试时长:120分钟
一、单选题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符
合题目要求的.
1.复数 ,则 等于( )
A.0 B. C.1 D.
2.已知集合 , ,则 等于( )
A. B. C. D.
3.设等差数列 的前 项和为 ,若 , ,则数列 的公差为( )
A.3 B.4 C.5 D.6
4.如图所示,矩形 的对角线相交于点O,E为 的中点,若 则
等于( )
A. B. C.1 D.-1
5.已知 是等比数列, ,前 项和为 ,则“ ”是“ 为递增数列”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
6. , , 的大小关系是( )
A. B.
C. D.
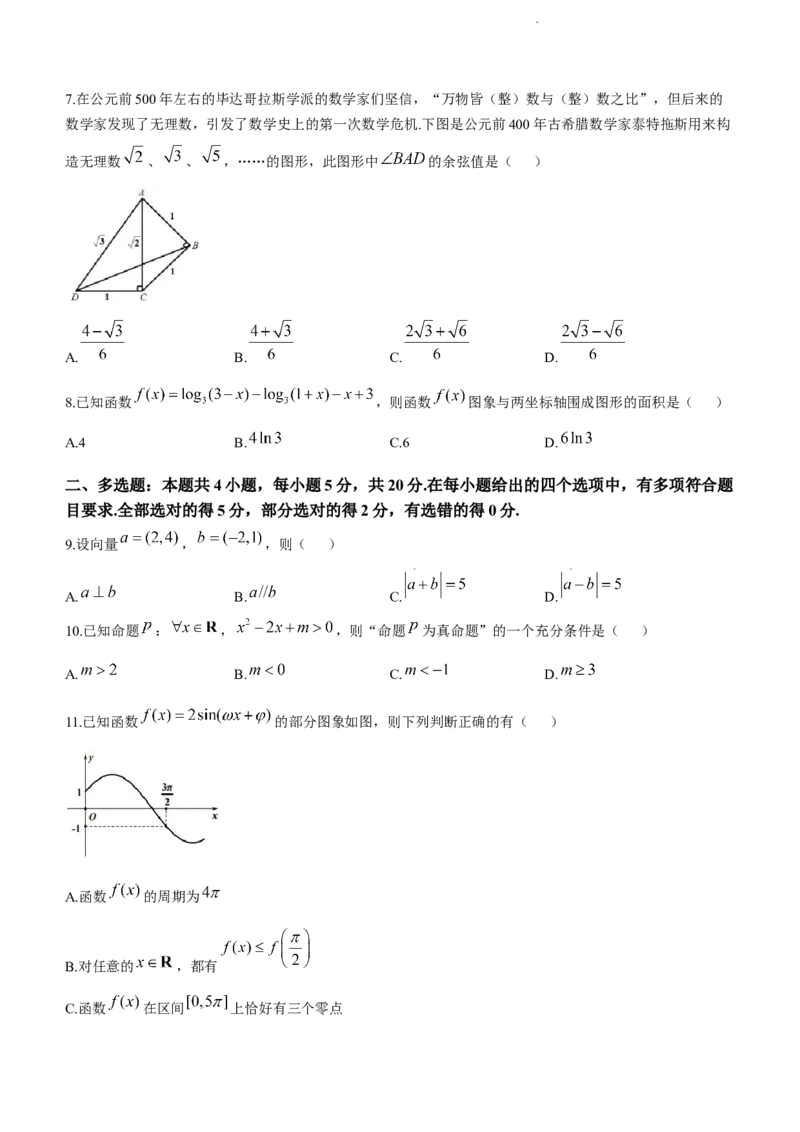
学科网(北京)股份有限公司7.在公元前500年左右的毕达哥拉斯学派的数学家们坚信,“万物皆(整)数与(整)数之比”,但后来的
数学家发现了无理数,引发了数学史上的第一次数学危机.下图是公元前400年古希腊数学家泰特拖斯用来构
造无理数 、 、 ,……的图形,此图形中 的余弦值是( )
A. B. C. D.
8.已知函数 ,则函数 图象与两坐标轴围成图形的面积是( )
A.4 B. C.6 D.
二、多选题:本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题
目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9.设向量 , ,则( )
A. B. C. D.
10.已知命题 : , ,则“命题 为真命题”的一个充分条件是( )
A. B. C. D.
11.已知函数 的部分图象如图,则下列判断正确的有( )
A.函数 的周期为
B.对任意的 ,都有
C.函数 在区间 上恰好有三个零点
学科网(北京)股份有限公司D.函数 是奇函数
12.已知数列 的通项公式是 ,在 和 之间插入1个数 ,使 , , 成等差数列;在
和 之间插入2个数 , ,使 , , , 成等差数列;……;在 和 之间插入 个数 ,
, , ,使 , , , , 成等差数列.这样得到新数列 : , , , ,
, , , , , , .记数列 的前 项和为 ,有下列选择支中,判断正确的是( )
A. B.
C. D.
三、填空题:本题共4小题,每小题5分,共20分.
13. __________.
14.设向量 ,向量 ,且 ,则 等于__________.
15.如图:直线 , 是 , 之间的一定点,并且 点到 , 的距离分别为2,4,过点 且夹角为
的两条射线分别与 , 相交于B,C两点,则 面积的最小值是__________.
16.若 存在单调递减区间,则正数 的取值范围是__________.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分10分)
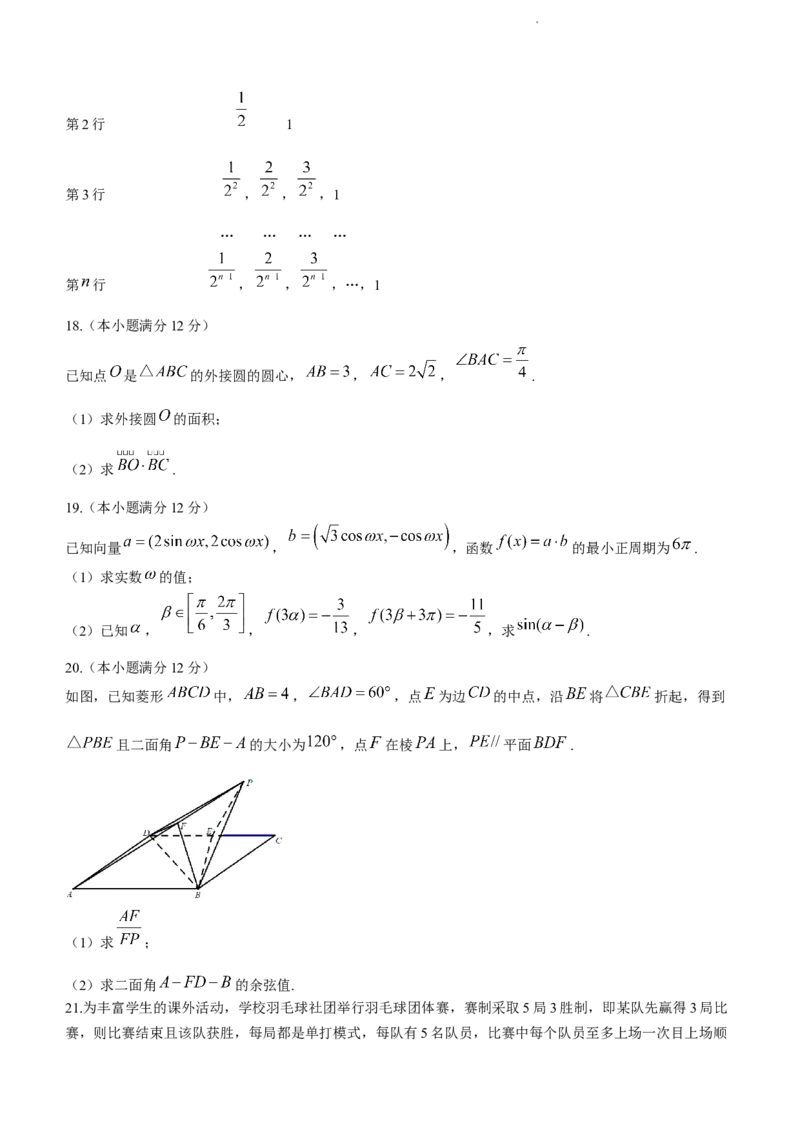
如图数表中,第 行中,第 个数为 ,共有 个数.
(1)求第 行所有数的和;
(2)求前10行所有数的和.
第1行 1
学科网(北京)股份有限公司第2行 1
第3行 , , ,1
… … … …
第 行 , , ,…,1
18.(本小题满分12分)
已知点 是 的外接圆的圆心, , , .
(1)求外接圆 的面积;
(2)求 .
19.(本小题满分12分)
已知向量 , ,函数 的最小正周期为 .
(1)求实数 的值;
(2)已知 , , , ,求 .
20.(本小题满分12分)
如图,已知菱形 中, , ,点 为边 的中点,沿 将 折起,得到
且二面角 的大小为 ,点 在棱 上, 平面 .
(1)求 ;
(2)求二面角 的余弦值.
21.为丰富学生的课外活动,学校羽毛球社团举行羽毛球团体赛,赛制采取5局3胜制,即某队先赢得3局比
赛,则比赛结束且该队获胜,每局都是单打模式,每队有5名队员,比赛中每个队员至多上场一次目上场顺
学科网(北京)股份有限公司序是随机的,每局比赛结果互不影响,经过小组赛后,最终甲乙两队进入最后的决赛,根据前期比赛的数据
统计,甲队明星队员M对乙队的每名队员的胜率均为 ,甲队其余4名队员对乙队每名队员的胜率均为 .
(注:比赛结果没有平局)
(1)若求甲队明星队员M在前三局比赛中出场,记前三局比赛中,甲队获胜局数为X,求随机变量X的分
布列及数学期望;
(2)若已知甲乙两队比赛3局,甲队以 获得最终胜利,求甲队明星队员M上场的概率.
22.已知函数 ,( , 是自然对数的底数).
(1)讨论 的单调性;
(2)当 时, ,求 的取值范围.
学科网(北京)股份有限公司南昌市三校(一中、十中、铁一中)高三上学期第一次联考
数学试卷参考答案
一、单选题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.【答案】C
【解析】 ,所以 .
2.【答案】B
解析:由 ,得到 ,即 ,由
即 ,则 .
3.【答案】C
【解析】 ,
故公差 .
答案:C.
4.【答案】A
【解析】 .
, , .
5.【答案】B
【解析】因为 是等比数列, ,所以
或 ,
为递增数列 ,所以是必要不充分条件.
6.【答案】B
【解析】 , , , ,
所以 .
7.【答案】D
学科网(北京)股份有限公司【解析】在 中, ,
在 中, .
8.【答案】A
【解析】
因此函数 的图象关于点 成中心对称, , ,函数 在区间 上单调递减,
因此与坐标轴围成图形的面积是 .
二、多选题:本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部
选对的得5分,部分选对的得2分,有选错的得0分.
9.【答案】ACD
【解析】因为 ,所以A正确,B不正确;
,所以 ,C正确;
,所以 ,D正确.
10.【答案】AD
11.【答案】BCD
【解析】由对称性知道, ,因此 ,A不正确;
,又 ,结合图象,可以取 ,即 ,因此
,因此B正确;
当 时, ,有三个零点,因此C正确;
是奇函数,因此D正确.
12.【答案】ABD
学科网(北京)股份有限公司【解析】A. ;
B. 在数列 中是第 项,所以 ;
C. ;
D.
.
三、填空题:本题共4小题,每小题5分,共20分.
13.【答案】
【解析】
,故答案为: .
14.【答案】
【解析】因为 ,则 ,即 ,
则 .
15.【答案】
【解析】设 与垂线的夹角为 ,则
, ,
学科网(北京)股份有限公司所以面积 ,
所以当 ,即当 时,面积最小,最小值是 .
16.【答案】
【解析】依题意 有解,即 ,
即 ,即 有解,
构造函数 ,单调递增,
因此不等式转化为 ,即 有解,
记 , ,
从而求得 ,因此 .
四、解答题:本题共6小题,共70分解答应写出文字说明、证明过程或演算步骤.
17.【解析】(1)第 行所有数的和为
;
(2)前10行所有数的和为
,
即 .
18.【解析】(1)由余弦定理得: .
学科网(北京)股份有限公司所以 ,因此 ,
所以外接圆的面积为 ;
(2)设 的中点为 ,则 ,
所以 .
19.【解析】(1)
,
所以 ;
(2)
又 ,所以 ,
,
又 ,所以 ,
所以 .
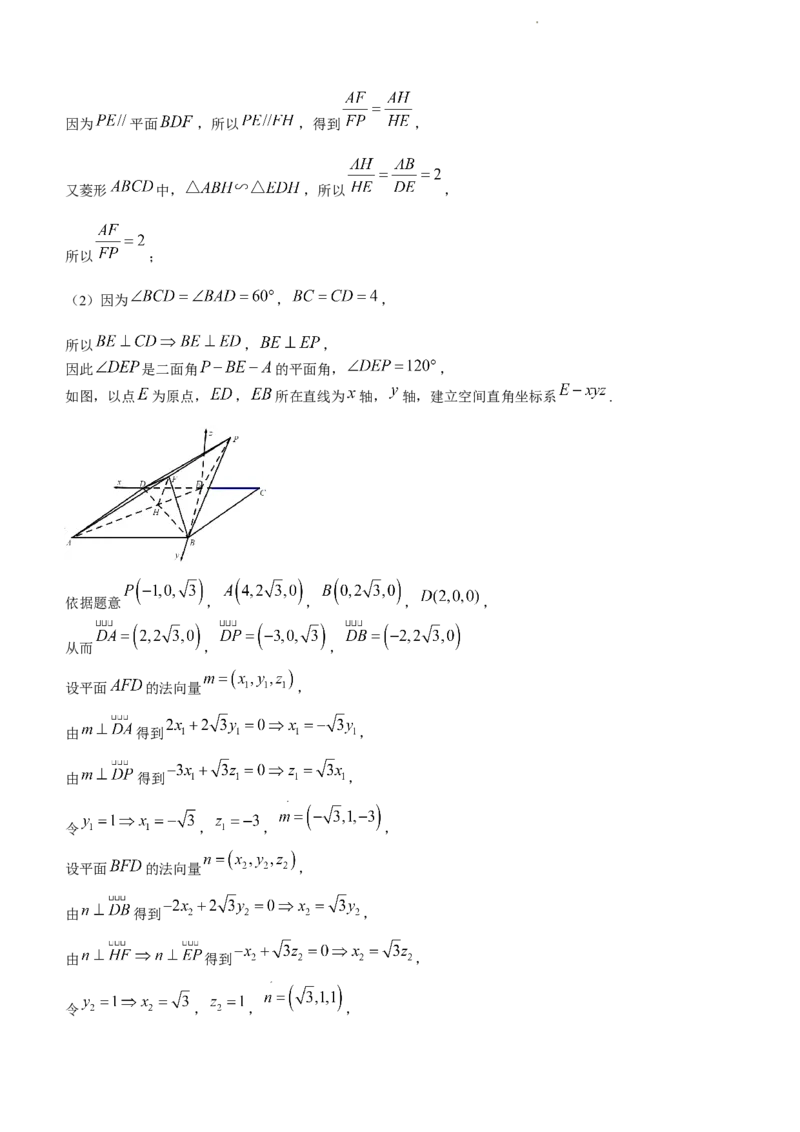
20.【解析】(1)连接 ,设 ,连接 ,
学科网(北京)股份有限公司因为 平面 ,所以 ,得到 ,
又菱形 中, ,所以 ,
所以 ;
(2)因为 , ,
所以 , ,
因此 是二面角 的平面角, ,
如图,以点 为原点, , 所在直线为 轴, 轴,建立空间直角坐标系 .
依据题意 , , , ,
从而 , ,
设平面 的法向量 ,
由 得到 ,
由 得到 ,
令 , , ,
设平面 的法向量 ,
由 得到 ,
由 得到 ,
令 , , ,
学科网(北京)股份有限公司因此 ,
所以,所求二面角的余弦值是 .
21.【解析】(1)Y可能取值有0,1,2,3.
,
,
,
,
因此,随机变量X的分布列是
X 0 1 2 3
P
数学期望 ;
(2)设 为甲3局获得最终胜利, 为前3局甲队明星队员 上场比赛, 为前3局甲队明星队员 没
有上场比赛,
因为每名队员上场顺序随机, , ,
,
,
甲队明星队员 上场的概率 .
学科网(北京)股份有限公司22.【解析】(1) ,
当 时, ,函数 在 上递减;
当 时,由 ,解得 ,故函数 在 上单调递减,
由 ,解得 ,故函数 在 上单调递增.
综上所述,当 时, 在 上递减;当 时, 在 上递减,在 上递增.
(2)当 时, ,
即 ,故 ,
令
,
则 ,
若 ,则当 时, ,函数 在 上单调递增,
当 时,
,
当 时, 单调递增,
则 ,符合题意;
若 ,则 ,
,
学科网(北京)股份有限公司由 得 ,
故 ,
存在 ,使得 ,
且当 时, ,
在 上单调递减,
当 时, ,不合题意,
综上,实数 的取值范围为 .
学科网(北京)股份有限公司