文档内容
成都石室中学 2024-2025 学年度上期高 2025 届定时练习
数 学
本试卷共8页。满分150分,考试时间120分钟。
注意事项:
1.答题前,务必将自己的姓名、班级、考号填写在答题卡规定的位置上。
2.答选择题时,必须使用2B铅笔将答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦擦干净
后,再选涂其它答案标号。
3.答非选择题时,必须使用0.5毫米黑色签字笔,将答案书写在答题卡规定的位置上。
4.所有题目必须在答题卡上作答,在试题卷上答题无效。
5.考试结束后,只将答题卡交回。
一、单选题
1、已知集合 ={ | =ln(5 ), }, ={ | =e },则 的子集个数为( )
A.4 B.14 C.15 D.16
− ∈ ∩
2、“ = 3”是“直线 :( +1) +2 +1= 0与直线 :3 + +1= 0平行”的( )
1 2
A.充要条件 B.必要不充分条件 C.充分不必要条件 D.既不充分也不必要条件
−
3、四川省将从2022年秋季入学的高一年级学生开始实行高考综合改革,高考采用“3+1+2”模式,其中“1”
为首选科目,即物理与历史二选一.某校为了解学生的首选意愿,对部分高一学生进行了抽样调查,制作出
如下两个等高堆积条形图,则下列结论正确的是( )
A.样本中选择物理意愿的男生人数少于选择历史意愿的女生人数
B.样本中女生选择历史意愿的人数多于男生选择历史意愿的人数
C.样本中选择物理学科的人数较多 D.样本中男生人数少于女生人数
4、已知{ }为等比数列, = , = 27,则 =( )
2 3 7 4 6 9 10 7
A.3 B.2 C. 2 D. 3
−
5、已知函数 ( )= ln 的图像与直线 = +1相切,则 的值为( )
− −
A. 1 B. 1 C.e D.e2
e e2
6、已知M,N分别是正四面体 中棱AD,BC的中点,若点E是棱CD的中点.则MN与AE所成角的余
弦值为( )
3 3 6 6
A. B. C. D.
3 3 6 6
− −
7、若 = sin 1 + 2, =cos 1 + 1,则( )
3 3 3 18
A. >1 > B. > >1 C.1> > D. >1>
8、若直线 和直线 相交于一点,将直线 绕该点按逆时针旋方向转到与 第一次重合时所转的角为 ,则
1 2 1 2
2 2
角 就叫做 到 的角 ,tan = 2 1,其中 , 分别是 , 的斜率,若双曲 线 : =1( >0, > 0)的右
1 2 1 + −1 2 1 2 1 2 2 2
2 −
焦点为 , 是右顶点, 是直线 = 上的一点, 是双曲线的离心率, = ,则tan 的最大值为
( ) ∠
学科网(北京)股份有限公司1 2
A. B. C. D.
2 1+ 1+ 2 1+ 2 1+2
二、多 选题
9、下列命题中,正确的是( )
A.已知随机变量 服从正态分布 (2, 2),若 ( 0)=0.3,则 ( <4)=0.3
B.用 表示 次伯努利试验中事件 发生的次数, 为每次试验中事件 发生的概率,若
≤
( ) = 150 , ( )=50,则 = 2
3
C.分 别抛掷两 枚 质地均匀的 硬币,设 =“第一枚正面朝上”, =“第二枚反面朝上”,
则有: ( )= ( )
D.已知 随 机∣ 变量 的分布列为 ( = )= ( =1,2,3, ,100),则 = 101
(+1) 100
10、设函数 ( ) = 3 3 2+ 1, 则 ( ) ⋯
A.当 <0时, =0是 ( )的极小值点
−
B.当0< <2时, ( )有三个零点
C.当 =1时,若 ( )在( 1, )上有最大值,则 >0
D.若 ( )满足 ( )+ (2 )= 2,则 =1
−
11、已知{ }满足 =1, 2 ( 1) 2 =0,记{ }的前n项和为 ,{ }的前n项和为
1 − +−1 +1 +1
,则下列说法中不一定正确的是( )
− − −
A .{ +1}是等比数列 B.{ }的通项公式为 =( 1)!或 =( 1) 1
−
C.若 >0,则 =( +1)! 1 D.若 < 0,则 − 为定 值 −
+1 2
三、填空题
−
12、若( +2) 5 = 5+ 4+ 3+ 2+ + ,则 5+ 3+ 1 = .
5 4 3 2 1 0
4+ 2+ 0
13、学校 从高一、高 二 、高 三 中各选 派 10名 同 学参加 “建 党 100周 年 党 史宣讲”系列报告会,其中三个年
级参会同学中女生人数分别为5、6、7,学习后学校随机选取一名同学汇报学习心得,结果选出一名女同
学,则该名女同学来自高三年级的概率为 .
14、已知不等式 e e + 对任意 R恒成立,则当 取最大值时, = .
四、解答题 − ≥ ∈
15、(本小题13分)
已知集合 ={ | 3<2 +1< 7}, ={ | +4>0}, ={ |3 2 +1}.
2
(1)求 ( ) ;− − − ≤ ≤
(2)若“ : ( )”是“ : ”的充分不必要条件,求实数 的取值范围.
∩
16、(本小题满分15分)
∈ ∪ ∈
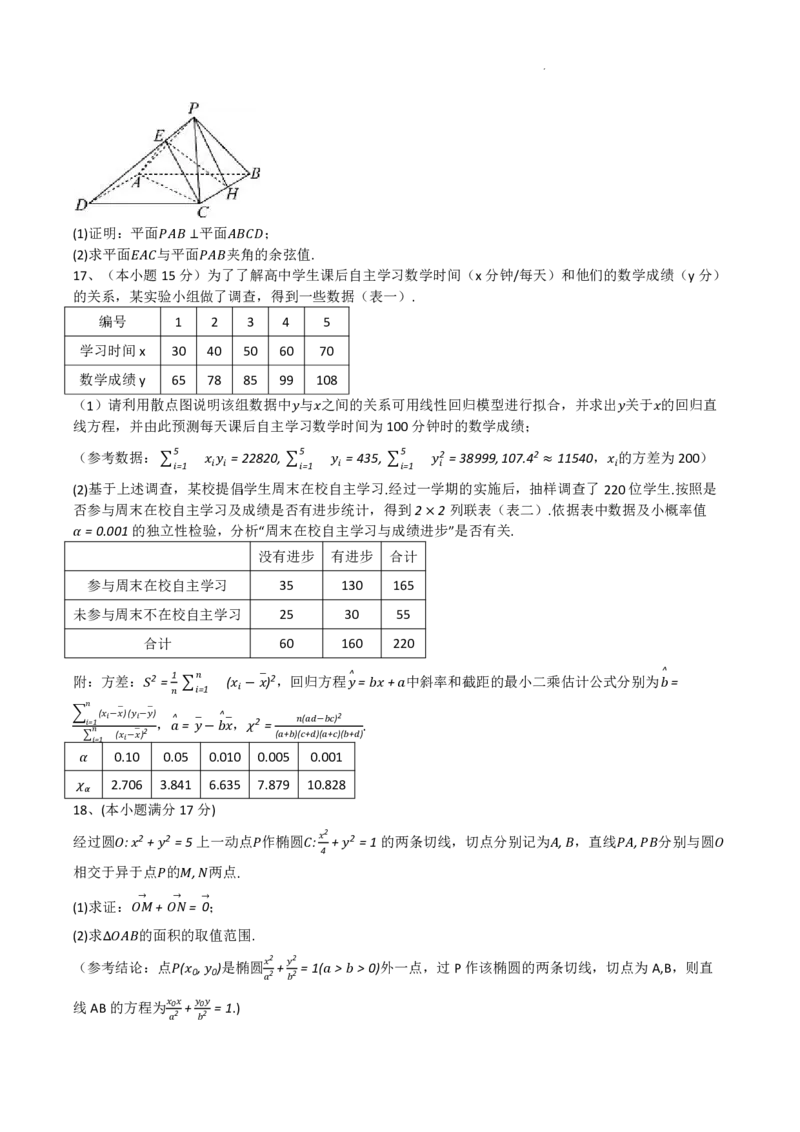
如图,在四棱锥 中,底面是边长为2的菱形, = π, 为 的中点, = = = 2.
3
为 上的一点, 已−知 =4 . ∠
学科网(北京)股份有限公司(1)证明:平面 平面 ;
(2)求平面 与平面 夹角的余弦值.
⊥
17、(本小题15分)为了了解高中学生课后自主学习数学时间(x分钟/每天)和他们的数学成绩(y分)
的关系,某实验小组做了调查,得到一些数据(表一).
编号 1 2 3 4 5
学习时间x 30 40 50 60 70
数学成绩y 65 78 85 99 108
(1)请利用散点图说明该组数据中 与 之间的关系可用线性回归模型进行拟合,并求出 关于 的回归直
线方程,并由此预测每天课后自主学习数学时间为100分钟时的数学成绩;
(参考数据: 5 =22820, 5 =435, 5 2 =38999,107.42 11540, 的方差为200)
=1 =1 =1
(2)基于上述调�查, 某校 提 倡学生周�末 在校自 主学习�.经 过一学 期的实施后,抽≈样调查了2 2 0位学生.按照是
否参与周末在校自主学习及成绩是否有进步统计,得到2 2列联表(表二).依据表中数据及小概率值
=0.001的独立性检验,分析“周末在校自主学习与成绩进步”是否有关.
×
没有进步 有进步 合计
参与周末在校自主学习 35 130 165
未参与周末不在校自主学习 25 30 55
合计 60 160 220
附:方差: 2 = 1 ( )2,回归方程 ^ = + 中斜率和截距的最小二乘估计公式分别为 ^ =
=1
−
=1 ( − )( − ) , ^ � = ^ , − 2 = ( )2 .
� =1 −( −)2 − − ( + ) ( + ) − ( + )( + )
−
� 0 . 1−0 0. 05 −0. 0 10 0.00 5 0.0 0 1
2.706 3.841 6.635 7.879 10.828
1 8 、(本小题满分17分)
2
经过圆 : 2+ 2 =5上一动点 作椭圆 : + 2 =1的两条切线,切点分别记为 , ,直线 , 分别与圆
4
相交于 异于 点 的 , 两点.
(1)求证: + = 0;
→ → →
(2)求 的 面积 的取值范围.
2 2
(参考Δ 结 论 :点 ( , )是椭圆 + =1( > >0)外一点,过P作该椭圆的两条切线,切点为A,B,则直
0 0 2 2
线AB的方程为 0 + 0 =1.)
2 2
学科网(北京)股份有限公司19、(本小题17分)
已知函数 ( )= ln + 1 2 + 3 ( >0)
4 4
(1)判断 ( )的 单 调性 ; −
(2)若 ( )有且仅有一个零点,求 的取值范围;
5 1
( )+
(3)若 取 第(2)问所求范围的最小值 ,且数列{ }满足, =2, = 4 4,
1 +1
−
求证: , | 1|< 4 .
=1 3
∗
∀ ∈ � −
学科网(北京)股份有限公司成都石室中学 2024-2025学年度上期高 2025届开学考试
数学参考答案
1-8DACDBDDC9BCD10BD11AB
12、【答案】
13、【答案】
14、【答案】e
15、【答案】(1)因为 ,又 ,..2分
所以 ………………………………………….………………5分
(2) ,所以 ………………7分
因为“ ”是“ ”的充分不必要条件,则 ,………9分
又 ,所以
或 ,…………..…………………12分
综上所述, 的取值范围为 .…………………………13分
16、【答案】(1)取 中点 ,连接 , ,
∵ , 为 中点,∴ ,…………….……1分
∵ , ,∴ ,
∵四边形 为菱形, ,∴ 为等边三角形,
∴ ,
又 , 分别为 , 中点,∴ ,
∴ ,即 ,………………………………………………………..3分
∵ , 平面 , 平面 ,∴ 平面 ,…5分
∵ 平面 ,∴平面 平面 .……………………………………………6分
(2)连接 ,由(1)知: 为等边三角形,∴ , ,
学科网(北京)股份有限公司又 平面 , ,∴ , ,………………7分
以 为坐标原点, , , 所在直线分别为 , , 轴,建立如图所示空间直角坐标系,
则 ,
∴ ,
由 得: ,
∴ ,
设平面 的法向量 ,则 ,
令 ,解得: ,∴ ,……………………………………10分
∵ 轴 平面 ,∴平面 的一个法向量 ,……………..………11分
设平面 与平面 的夹角为 ,则
………………………………………….…14分
所以平面 与平面 夹角的余弦值为 …...……………………………………15分
17、【答案】(1)画出散点图(图略)可以得到这些样本点在某一条直线附近波动,说明该组数据中 与
之间的关系可用线性回归模型进行拟合.………………………2分
, ,又 的方差为 ,
,………………………7分
学科网(北京)股份有限公司,故 当 时, ,故预测每天课后自主学习数
学时间达到100分钟时的数学成绩为140.5分………………………9分
(2)零假设 :周末在校自主学习与成绩进步无关………………………10分
根据数据,计算得到:
………………13分
因为 ,所以依据小概率值 的独立性检验,我们推断H 不成立,可以认为“周末自
0
主学习与成绩进步”有关.,此推断犯错误的概率不大于0.001………15分
18、【答案】(1)证明:设点 .
①当直线 的斜率都存在时,设过点 与椭圆 相切的直线方程为 .
联立 ,消去 得: ,
,…………………………………………….…2分
令 ,整理得: .………….…3分
设直线 的斜率分别为 .
∴ .又 ,∴ .
∴ ,即 为圆 的直径,
∴ .………………………………….…5分
②当直线 或 的斜率不存在时,不妨设 ,则直线 的方程为
∴点 ,点 ,也满足 .……………………………………….………….…6分
综上所述,证得 .……………………………………………………………………………………..…7分
(2)设点 ,则直线 的方程为 .………………………………………..…8分
若 时,令 ,则直线 的方程为 , ,
学科网(北京)股份有限公司∴ .………………………………………………………………………………….…9分
若 时,联立 ,消去 得 .
∴ , ,………………………………………………………………………..…11分
∴
.……………………………………………..………………..…13分
又点 到直线 的距离: .…………………………………….…..…14分
,……………………………………………………..…15分
令 , .则 ,又 ,…………..….…16分
∴ 的面积的取值范围为 .……………………………………………………………………………..…17分
19、【答案】(1) 1分
,令 ,对称轴 , ,
1当 时, ,则 , 在 单调递增2分
2当 时, ,令 ,得 ,
时,则 , ; 时,则 , ; 时,则
, 在 上单调递增, 上单调递减, 上单调递增4分
综上, 时, 在 单调递增; 时, 在 上单调递
增, 上单调递减, 上单调递增.5分
(2)易知 ,由(1)可得
1当 时, 在 单调递增,又
有且仅有一个零点 6分
学科网(北京)股份有限公司2 时, 在 上单调递增, 上单调递减, 上单
调递增; ,又 ,
,
在 上有一个零点 ;
又 时, ; 时, 在 上各有有一
个零点; 有三个零点8分
综上 9分
(3) ,
令 ,
,所以 在 上单调递增,
所以当 时, ,所以 ,即 ,
所以由 可得当 ,则
因此,若存在正整数 ,使得 ,则 ,从而 ,重复这一过程有限次后可得 ,与
矛盾,从而,对 ,11分
下面我们先证明,当 时, ,
设 ,则当 时, ,所以 在 单调递
减,所以 ,即当 时, 12分
因为 ,所以 ,
,
即 ,由于 , ,所以 , ,故 15分
故当 时, 16分
学科网(北京)股份有限公司所以 ,故 , .17分
学科网(北京)股份有限公司