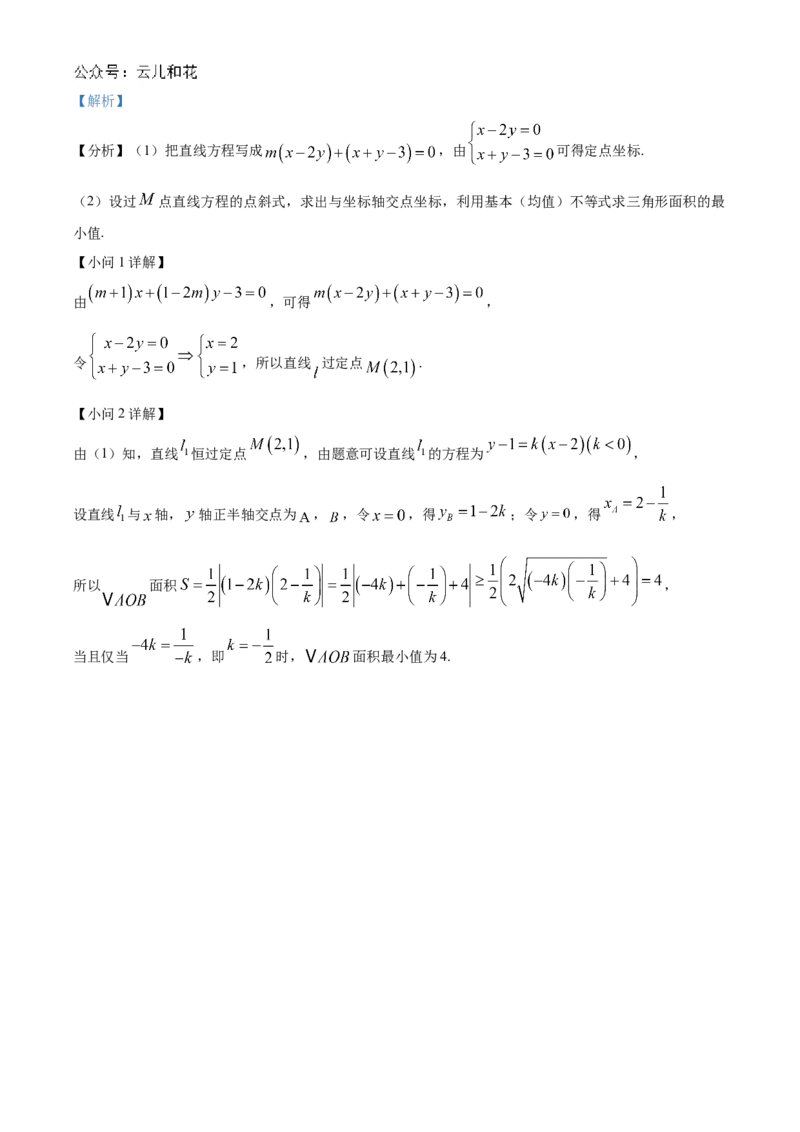文档内容
2024-2025 学年度第一学期高二期中测试
数学试题
本试卷共4页,22小题,满分150分.考试用时120分钟.
注意事项:
1.答题前,考生务必用黑色字迹钢笔或签字笔将自己的姓名、考生号、考场号和座位号填写
在答题卡上.用2B铅笔将试卷类型填涂在答题卡相应位置上.将条形码横贴在答题卡右上角“条
形码粘贴处”.
2.作答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目选项的答案信息点涂
黑;如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上.
3.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应
位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液.不按
以上要求作答的答案无效.
4.考生必须保持答题卡的整洁.考试结束后,将试卷和答题卡一并交回.
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是
符合题目要求的.
1. 若复数z满足 ,则 ( )
A. B. C. D.
【答案】B
【解析】
【分析】设 ,利用复数的运算得到 ,再结合条件,求得 ,即
可求解.
【详解】设 ,则 ,
又 ,得到 ,所以 , ,所以 , 或 , ,得到 ,
所以 ,
故选:B.
2. 已知平面上的两个非零向量 , 满足 ,则 ( )
A. B. C. D.
【答案】B
【解析】
【分析】借助向量数量积公式计算可得 ,再利用向量夹角公式计算即可得.
【详解】由 ,故 ,
则 ,又 ,故 .
故选:B.
3. 函数 在区间 单调递减,则实数 取值范围是( )
A. B. C. D.
【答案】D
【解析】
【分析】 时,代入可知满足题意; 时,求出二次函数的对称轴结合函数在右半部分单调递减得
出开口方向,列出不等式组,求解即可得出答案.
【详解】当 时, 在 上单调递减,满足题意;
当 时, 的对称轴为直线 ,由 在 上单调递减,知 ,解得 .
综上,a的取值范围为 .
故选:D
4. ( )
A. B. C. D.
【答案】D
【解析】
【分析】利用诱导公式以及逆用两角和的正弦公式求解.
【详解】
.
故选:D
的
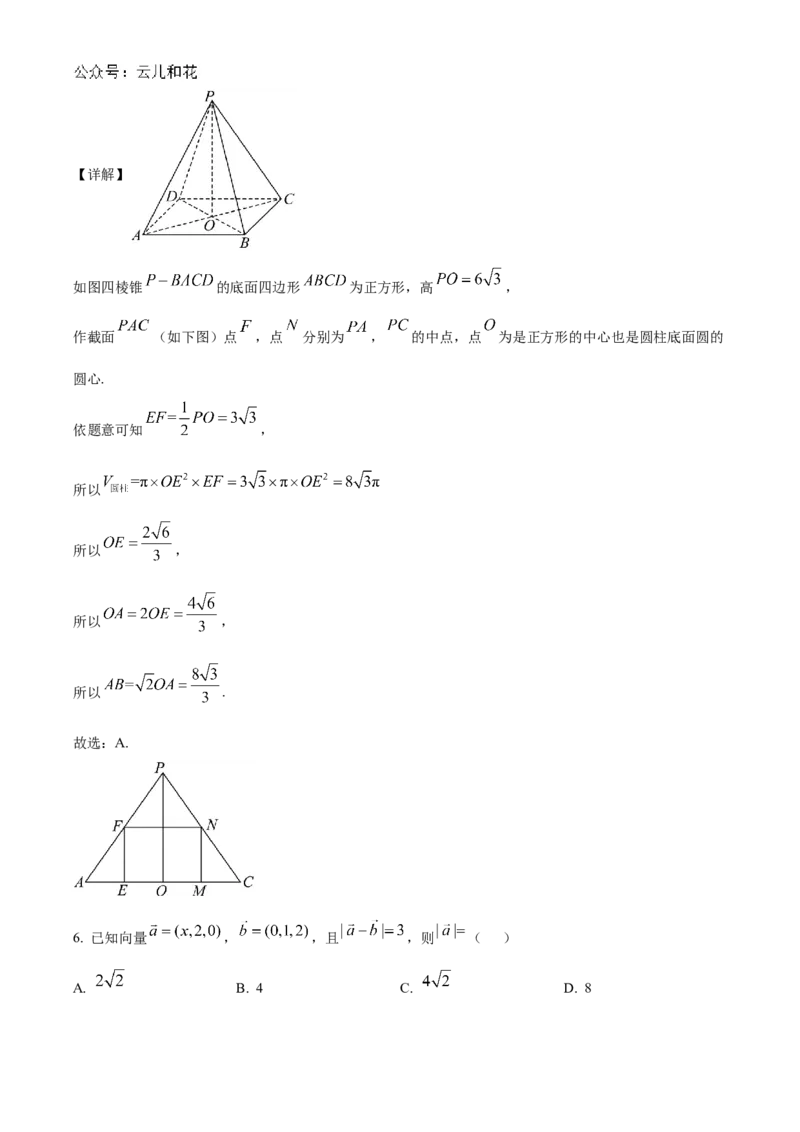
5. 已知四棱锥 底面是正方形,顶点在底面的射影是底面的中心,高为 .若圆柱的一个底面的圆周经
过四棱锥四条侧棱的中点,另一个底面的圆心为四棱锥底面的中心,且该圆柱的体积为 ,则四棱锥
的底面的边长为( )
A. B. 6 C. D. 9
【答案】A
【解析】
【分析】作出组合体的截面 ,确定圆柱的高,利用圆柱的体积求得圆柱底面的半径,进而得到底面
正方形的边长.【详解】
如图四棱锥 的底面四边形 为正方形,高 ,
作截面 (如下图)点 ,点 分别为 , 的中点,点 为是正方形的中心也是圆柱底面圆的
圆心.
依题意可知 ,
所以
所以 ,
所以 ,
所以 .
故选:A.
6. 已知向量 , ,且 ,则 ( )
A. B. 4 C. D. 8【答案】A
【解析】
【分析】先求出 的坐标,利用模长公式求出参数 ,再求 .
【详解】 , , ,
∵ ,∴ , ,
所以 ,
故选:A.
7. 已知 ,且 ,则 的最大值为( )
A. 9 B. 12 C. 36 D. 48
【答案】C
【解析】
【分析】设A(x ,y )与B(x ,y ), 为 的中点,可证明点 在以 为圆心,2为半径的圆上,由
1 1 2 2
,结合两点距离的几何意义即可求解.
【详解】设A(x ,y )与B(x ,y )为圆 上一点,
1 1 2 2
则 ,得 , ,
即 为等腰直角三角形,设 为 的中点,
则 ,得 ,
即点 在以 为圆心,2为半径的圆上,
故 ,
因为点 到定点D(1,0)的距离的最大值为 ,
因此 的最大值为36.故选:C
【点睛】关键点点睛:解决本题的关键是将原问题化为 ,
根据两点距离的几何意义求解即可.
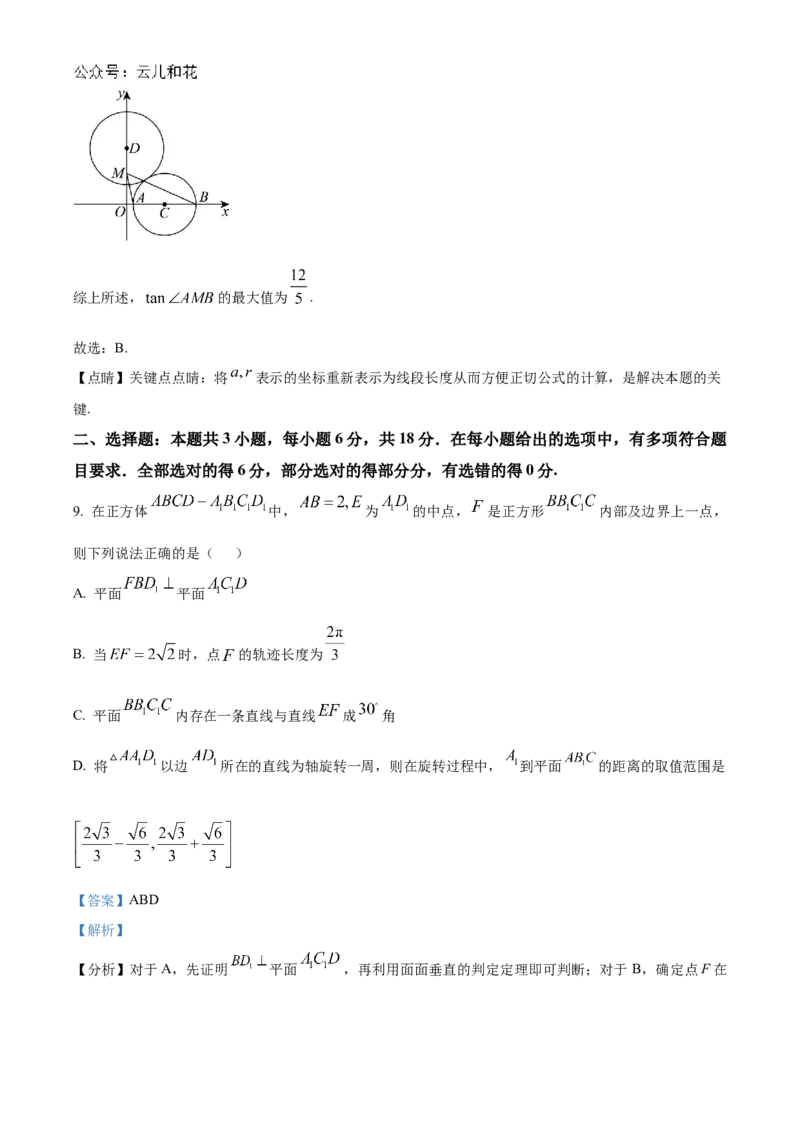
8. 已知圆D: 与x轴相交于A、B两点,且圆C: ,点
.若圆C与圆D相外切,则 的最大值为( )
A. B. C. D.
【答案】B
【解析】
【分析】根据圆 与圆 相外切,可得 ,再根据圆的对称性不妨令 ,再分
, 和 三种情况讨论即可.
【详解】圆D: 的圆心 ,半径为 ,
圆C: 的圆心 ,半径为 ,
因为圆 与圆 相外切,所以 ,所以 ,
且圆 与 轴交于 ,不妨记 ,
因为圆 关于 轴对称,点 与点 关于 轴对称,点 在 轴上,
由对称性不妨令 ,当 时,则 ,解得 ,
故
,
当 时,则 ,解得 ,
此时 ,
故 ,
当 时,则 ,解得 ,
故
,综上所述, 的最大值为 .
故选:B.
【点睛】关键点点睛:将 表示的坐标重新表示为线段长度从而方便正切公式的计算,是解决本题的关
键.
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题
目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9. 在正方体 中, 为 的中点, 是正方形 内部及边界上一点,
则下列说法正确的是( )
A. 平面 平面
B. 当 时,点 的轨迹长度为
C. 平面 内存在一条直线与直线 成 角
D. 将 以边 所在的直线为轴旋转一周,则在旋转过程中, 到平面 的距离的取值范围是
【答案】ABD
【解析】
【分析】对于A,先证明 平面 ,再利用面面垂直的判定定理即可判断;对于 B,确定点F在以H为圆心,半径为2的圆上运动,结合弧长公式即可判断;对于C,求出EF与平面 所成角的最
小值,即可判断;对于D,判断出点 的运动轨迹,进而结合圆的几何性质进行求解.
【详解】对于A,连接 ,则 ,
又 平面 平面 ,故 ,
平面 ,故 平面 ,
平面 ,故 ,同理 ,
平面 ,故 平面 ,
平面 ,故平面 平面 ,A正确;
对于B,取 的中点为H,连接 ,
则 平面 , 平面 ,故 ,
由于 ,故 ,即点F在以H为圆心,半径为2的圆上运动,
结合题意知F轨迹为该圆在平面 内的圆弧,如图圆弧,
则 ,则 ,
故F轨迹长度为 ,B正确;
对于C,从正方体中分离出四棱锥 , 的中点为H,
平面 ,则 ,
,
则EF与平面 所成角的最小值为 , ,
即 ,故平面 内不存在一条直线与直线 成 角,C错误;
对于D,连接 交 于N,取 的中点为M,连接 ,则点 的轨迹为平面 内以N为圆心, 为半径的圆,
又正方体性质知 ,由 知 ,
而 平面 ,故 平面 ,
平面 ,故平面 平面 ;
又 平面 平面 ,故 ,
结合 , 平面 ,
故 平面 , 平面 ,
故 ,则 ,
设 与圆的交点分别为 ,
当点 位于 处时, 到平面 的距离分别取到最大值和最小值,
最大值为 ,
最大值为 ,
故 到平面 的距离的取值范围是 ,D正确
故选:ABD.
【点睛】难点点睛:解答本题的难点在于选项D的判断,解答时要注意判断出点 的运动轨迹,进而结合
圆的几何性质进行求解.
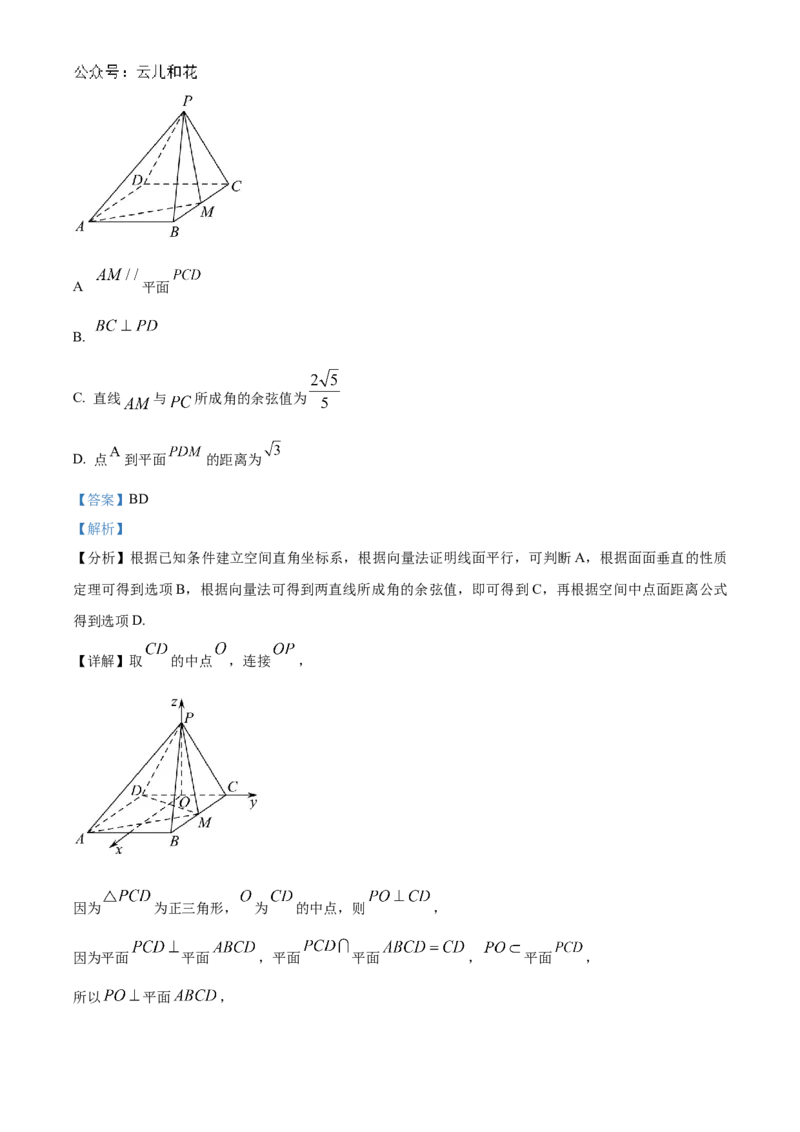
10. 如图,四边形 为正方形,平面 平面 ,且 为正三角形, 为
的中点,则下列命题中正确的是( ).
A 平面
B.
C. 直线 与 所成角的余弦值为
D. 点 到平面 的距离为
【答案】BD
【解析】
【分析】根据已知条件建立空间直角坐标系,根据向量法证明线面平行,可判断A,根据面面垂直的性质
定理可得到选项B,根据向量法可得到两直线所成角的余弦值,即可得到C,再根据空间中点面距离公式
得到选项D.
【详解】取 的中点 ,连接 ,
因为 为正三角形, 为 的中点,则 ,
因为平面 平面 ,平面 平面 , 平面 ,
所以 平面 ,又因为四边形 为正方形,以点 为原点, 的方向为 轴的正方向,
建立空间直角坐标系,如图所示,
, ,
对于A, ,由图易知平面 的一个法向量为 ,
因为 ,故 与平面 不平行,故A错误;
对于B,因为四边形 为正方形,所以 ,
因为平面 平面 ,平面 平面 , 平面 ,
所以 平面 ,又 平面 ,所以 ,故B正确;
对于C, , ,
,
所以直线 与 所成角的余弦值为 ,故C错误;
对于D, ,
设平面 的法向量为 ,则 ,
令 ,则 ,所以 ,
点 到平面 的距离 ,故选项D正确;
故选:BD.
11. 点A,B为圆 上的两点,点 为直线 上的一个动点,则下列说法
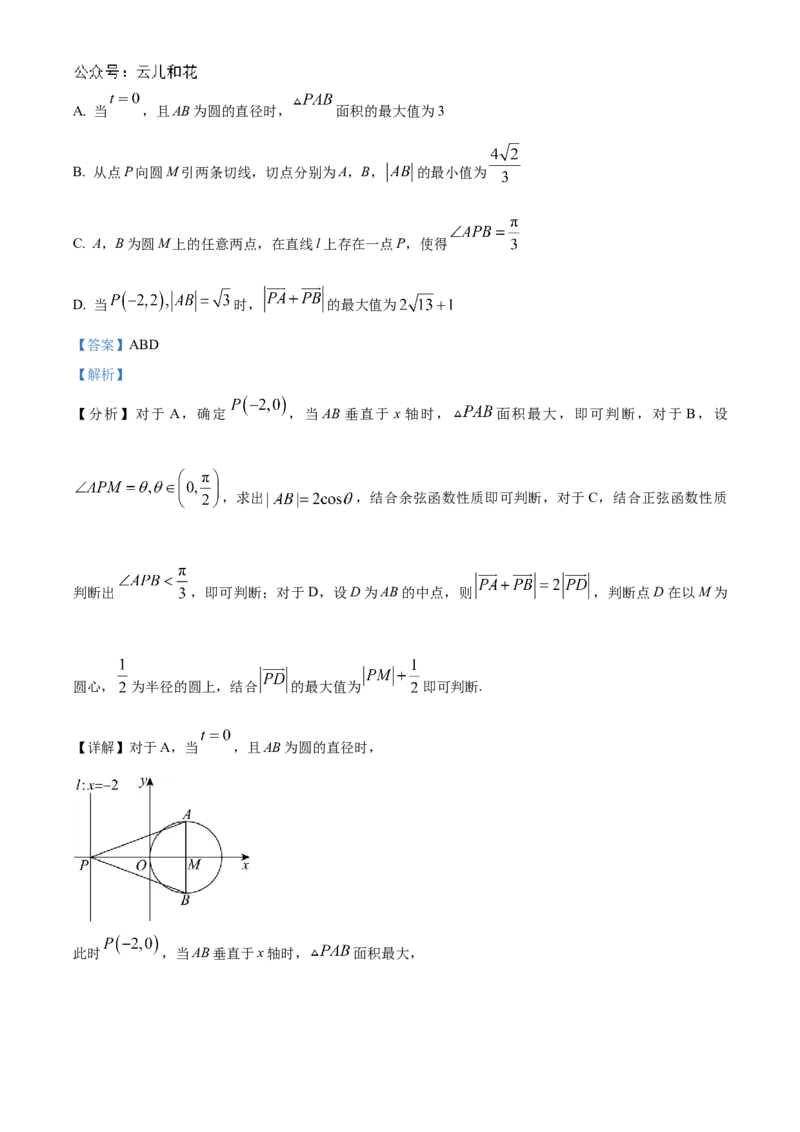
正确的是( )A. 当 ,且AB为圆的直径时, 面积的最大值为3
B. 从点P向圆M引两条切线,切点分别为A,B, 的最小值为
C. A,B为圆M上的任意两点,在直线l上存在一点P,使得
D. 当 时, 的最大值为
【答案】ABD
【解析】
【分析】对于 A,确定 ,当 AB 垂直于 x 轴时, 面积最大,即可判断,对于 B,设
,求出 ,结合余弦函数性质即可判断,对于C,结合正弦函数性质
判断出 ,即可判断;对于D,设D为AB的中点,则 ,判断点D在以M为
圆心, 为半径的圆上,结合 的最大值为 即可判断.
【详解】对于A,当 ,且AB为圆的直径时,
此时 ,当AB垂直于x轴时, 面积最大,不妨取 ,则 ,A正确;
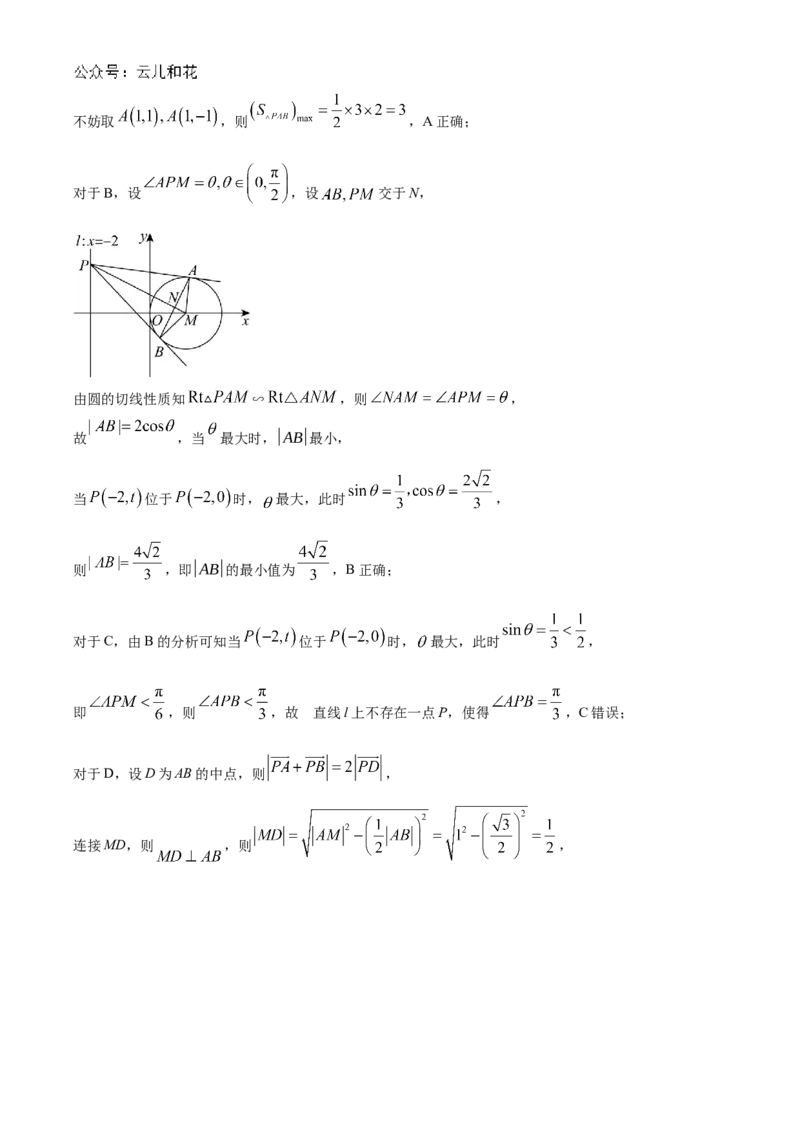
对于B,设 ,设 交于N,
由圆的切线性质知 ∽ ,则 ,
故 ,当 最大时,|AB|最小,
当 位于 时, 最大,此时 ,
则 ,即|AB|的最小值为 ,B正确;
对于C,由B的分析可知当 位于 时, 最大,此时 ,
即 ,则 ,故 在直线l上不存在一点P,使得 ,C错误;
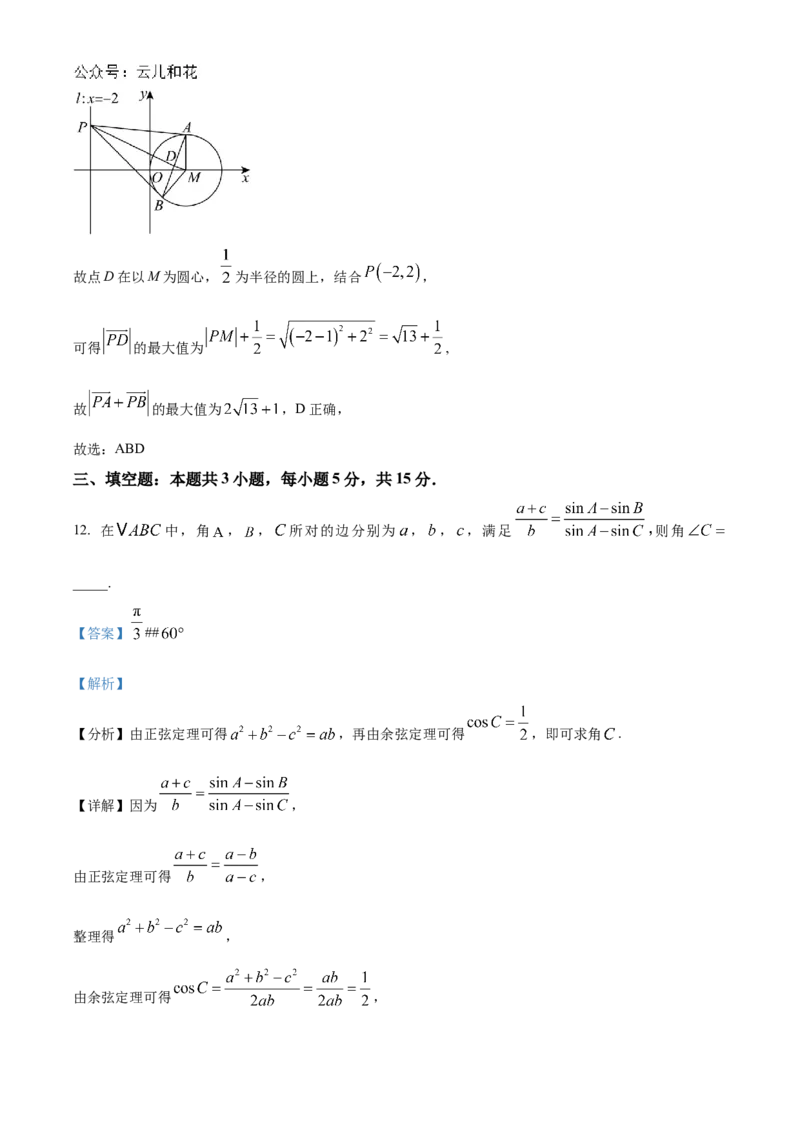
对于D,设D为AB的中点,则 ,
连接MD,则 ,则 ,故点D在以M为圆心, 为半径的圆上,结合 ,
可得 的最大值为 ,
故 的最大值为 ,D正确,
故选:ABD
三、填空题:本题共3小题,每小题5分,共15分.
12. 在 中,角 , , 所对的边分别为 , , ,满足 则角
_____.
【答案】 ##
【解析】
【分析】由正弦定理可得 ,再由余弦定理可得 ,即可求角 .
【详解】因为 ,
由正弦定理可得 ,
整理得 ,
由余弦定理可得 ,因为 ,
所以 .
故答案为:
13. 已知正四面体 的边长为2,点M,N为棱BC,AD的中点,点E,F分别为线段AM,CN上的
动点,且满足 ,则线段EF长度的最小值为__________.
【答案】
【解析】
【分析】根据给定条件,取定空间的基底 ,利用空间向量的线性运算表示向量 ,再利
用向量数量积的运算律,结合二次函数求出最小值.
【详解】在棱长为2的正四面体 中,由点M,N为棱BC,AD的中点,得 ,
由点E,F分别在线段AM,CN上, ,令 ,则 ,
所以
,又 ,
, ,
故
,
当 时, ,所以线段EF长度的最小值为 .故答案为:
【点睛】思路点睛:取定空间的一个基底,表示向量 ,再利用向量运算求解.
14. 已知曲线 与直线 有且仅有一个公共点,那么实数 的取值范围是
______.
【答案】
【解析】
【分析】根据方程可知直线恒过定点,曲线为半圆,画出图象,数形结合可得到 的取值范围.
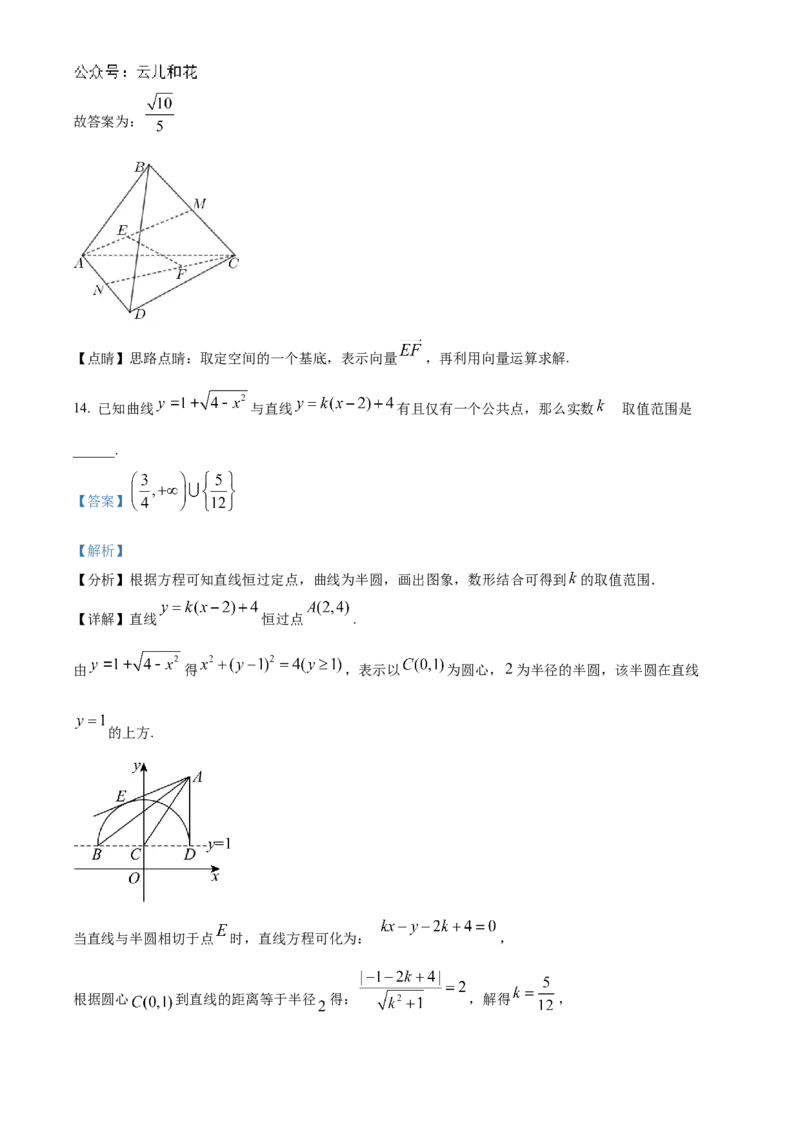
【详解】直线 恒过点 .
由 得 ,表示以 为圆心, 为半径的半圆,该半圆在直线
的上方.
当直线与半圆相切于点 时,直线方程可化为: ,
根据圆心 到直线的距离等于半径 得: ,解得 ,当直线过点 时, ,此时直线与曲线有两个公共点,
当直线过点 时,直线斜率不存在,此时直线与曲线有一个公共点,
综上得,实数 的取值范围是 .
故答案为: .
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15. 的内角 的对边分别为 ,已知 .
(1)求角 ;
(2)若 , 的面积为 ,求 .
【答案】(1)
(2)
【解析】
【分析】(1)由正弦定理边化角,即可求得答案;
(2)由三角形面积求出c,再利用余弦定理即可求得答案.
【小问1详解】
由题意知 ,即 ,
由于 ,
故 ,即 ,结合 ,则 ;
【小问2详解】
, , 的面积为 ,则 ,则 ,故 ,
故 .
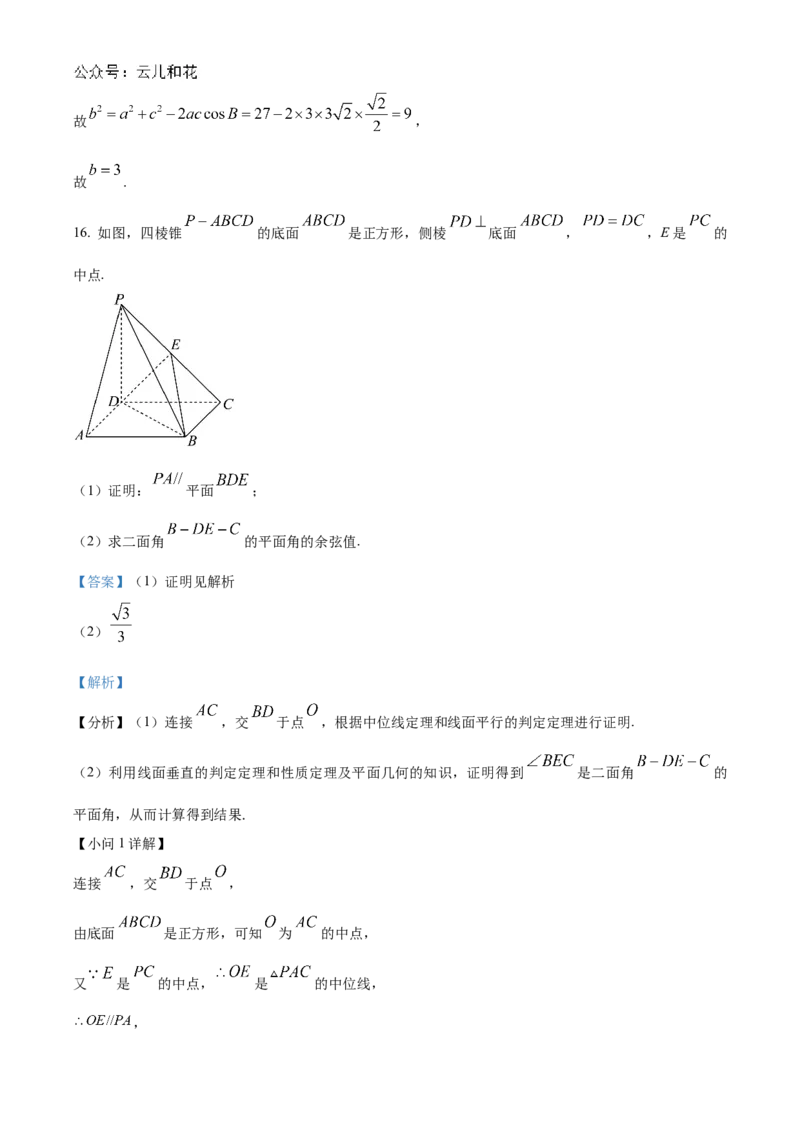
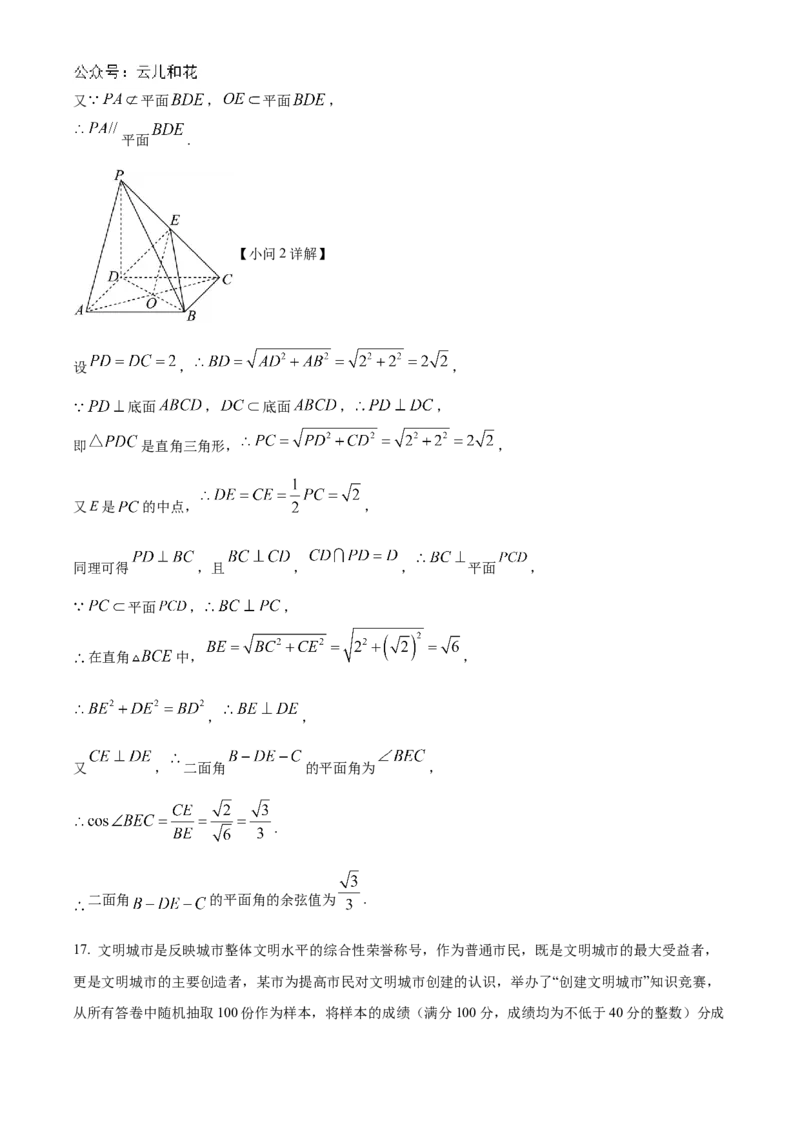
16. 如图,四棱锥 的底面 是正方形,侧棱 底面 , ,E是 的
中点.
(1)证明: 平面 ;
(2)求二面角 的平面角的余弦值.
【答案】(1)证明见解析
(2)
【解析】
【分析】(1)连接 ,交 于点 ,根据中位线定理和线面平行的判定定理进行证明.
(2)利用线面垂直的判定定理和性质定理及平面几何的知识,证明得到 是二面角 的
平面角,从而计算得到结果.
【小问1详解】
连接 ,交 于点 ,
由底面 是正方形,可知 为 的中点,
又 是 的中点, 是 的中位线,
,又 平面 , 平面 ,
平面 .
【小问2详解】
设 , ,
底面 , 底面 , ,
即 是直角三角形, ,
又E是 的中点, ,
同理可得 ,且 , , 平面 ,
平面 , ,
在直角 中, ,
, ,
又 , 二面角 的平面角为 ,
.
二面角 的平面角的余弦值为 .
17. 文明城市是反映城市整体文明水平的综合性荣誉称号,作为普通市民,既是文明城市的最大受益者,
更是文明城市的主要创造者,某市为提高市民对文明城市创建的认识,举办了“创建文明城市”知识竞赛,
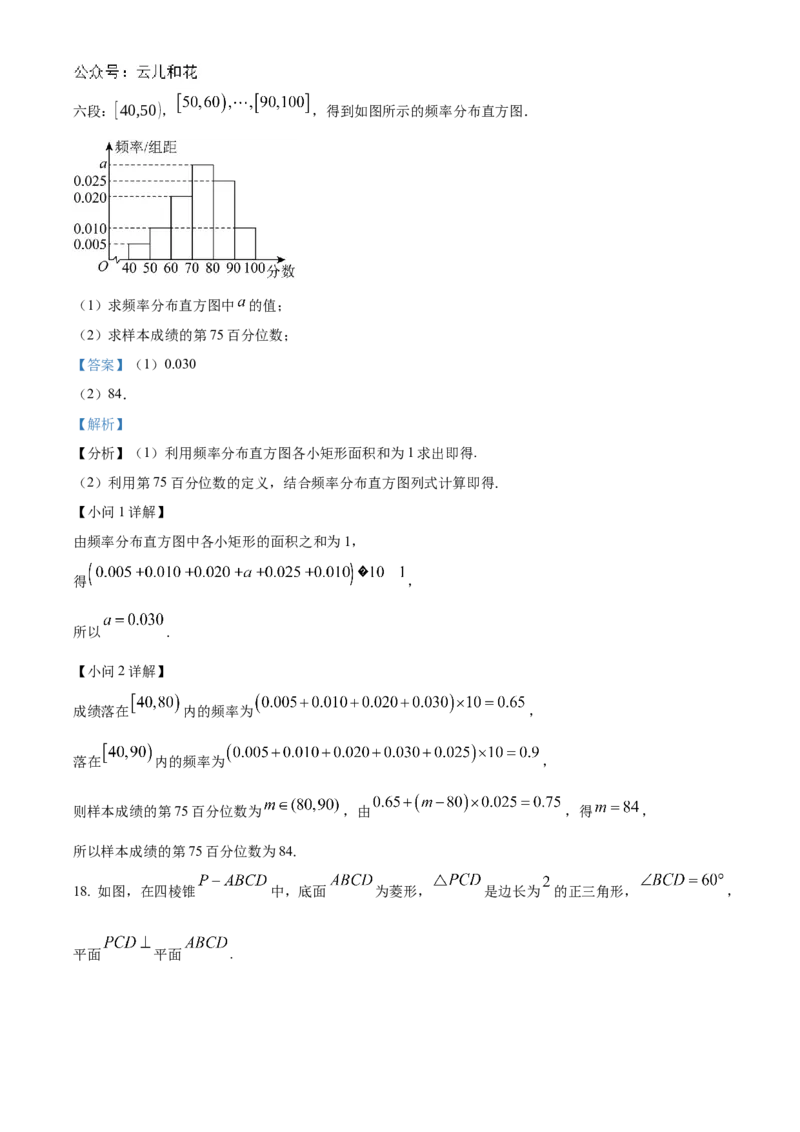
从所有答卷中随机抽取100份作为样本,将样本的成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50), ,得到如图所示的频率分布直方图.
(1)求频率分布直方图中 的值;
(2)求样本成绩的第75百分位数;
【答案】(1)0.030
(2)84.
【解析】
【分析】(1)利用频率分布直方图各小矩形面积和为1求出即得.
(2)利用第75百分位数的定义,结合频率分布直方图列式计算即得.
【小问1详解】
由频率分布直方图中各小矩形的面积之和为1,
得 ,
所以 .
【小问2详解】
成绩落在 内的频率为 ,
落在 内的频率为 ,
则样本成绩的第75百分位数为 ,由 ,得 ,
所以样本成绩的第75百分位数为84.
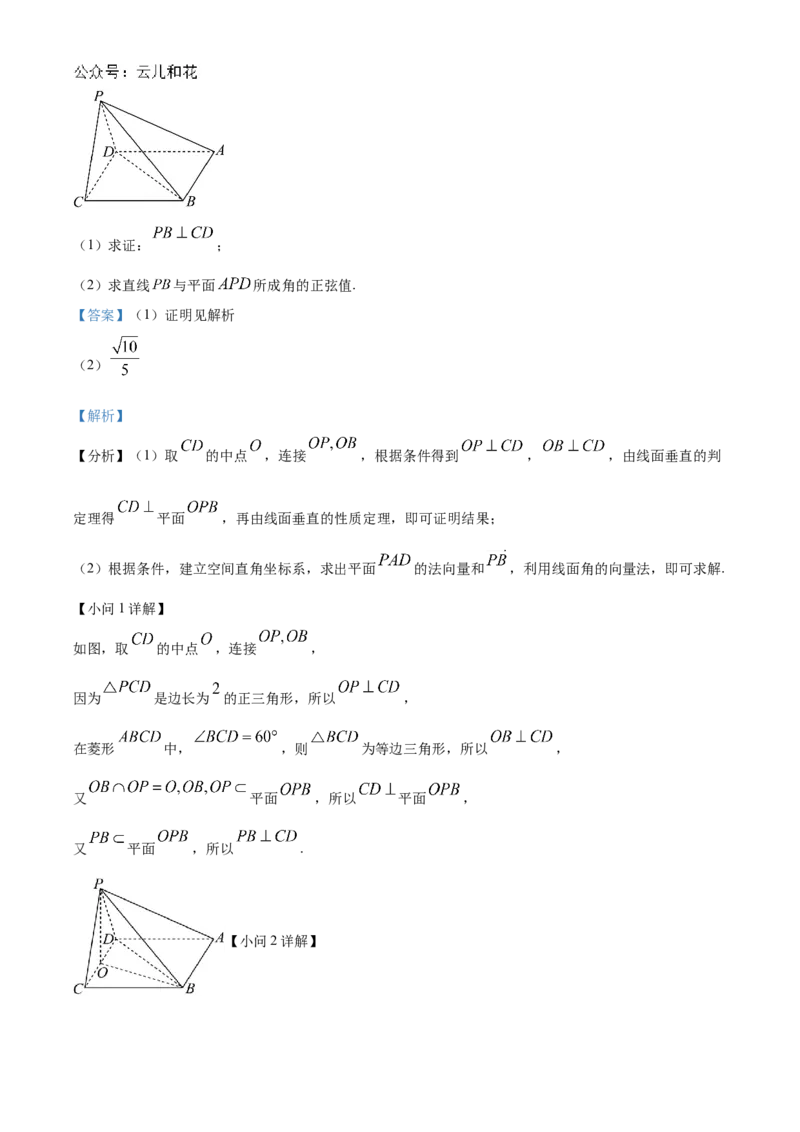
18. 如图,在四棱锥 中,底面 为菱形, 是边长为 的正三角形, ,
平面 平面 .(1)求证: ;
(2)求直线 与平面 所成角的正弦值.
【答案】(1)证明见解析
(2)
【解析】
【分析】(1)取 的中点 ,连接 ,根据条件得到 , ,由线面垂直的判
定理得 平面 ,再由线面垂直的性质定理,即可证明结果;
(2)根据条件,建立空间直角坐标系,求出平面 的法向量和 ,利用线面角的向量法,即可求解.
【小问1详解】
如图,取 的中点 ,连接 ,
因为 是边长为 的正三角形,所以 ,
在菱形 中, ,则 为等边三角形,所以 ,
又 平面 ,所以 平面 ,
又 平面 ,所以 .
【小问2详解】由(1)得 ,
因为平面 平面 ,平面 平面 平面 ,
所以 平面 ,
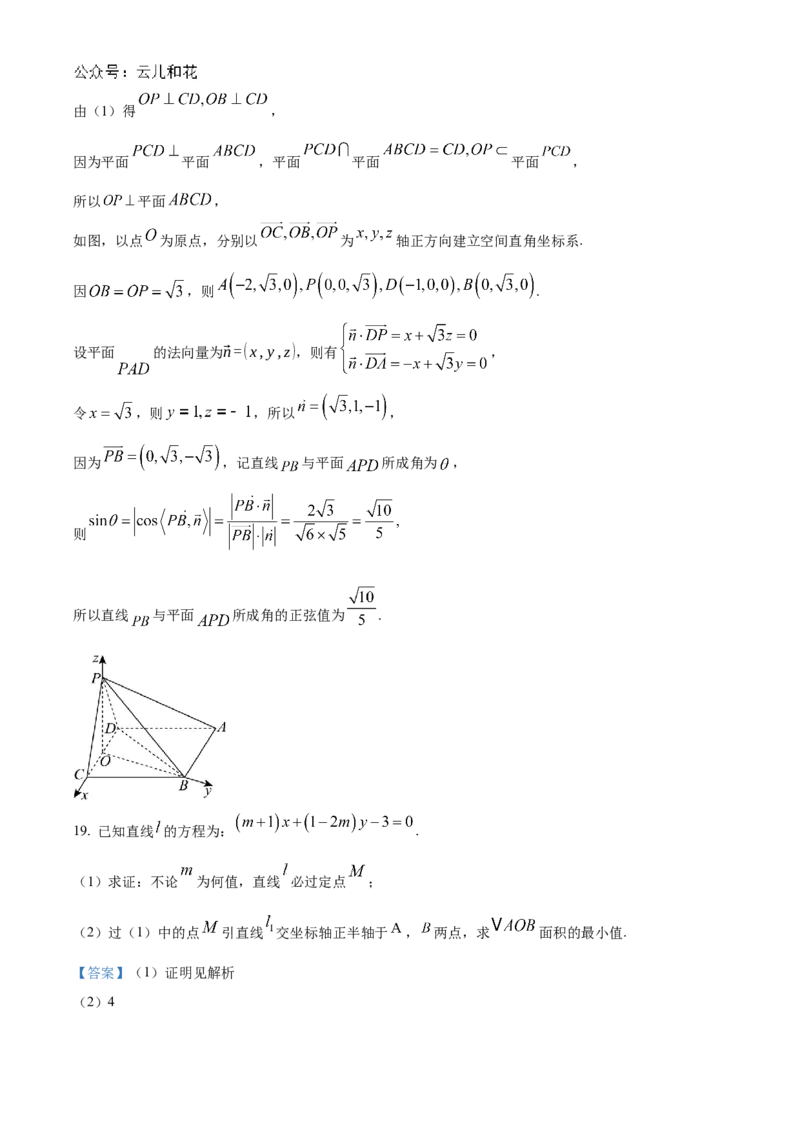
如图,以点 为原点,分别以 为 轴正方向建立空间直角坐标系.
因 ,则 .
设平面 的法向量为⃗n=(x,y,z),则有 ,
令 ,则 ,所以 ,
因为 ,记直线 与平面 所成角为 ,
则
所以直线 与平面 所成角的正弦值为 .
19. 已知直线 的方程为: .
(1)求证:不论 为何值,直线 必过定点 ;
(2)过(1)中的点 引直线 交坐标轴正半轴于 , 两点,求 面积的最小值.
【答案】(1)证明见解析
(2)4【解析】
【分析】(1)把直线方程写成 ,由 可得定点坐标.
(2)设过 点直线方程的点斜式,求出与坐标轴交点坐标,利用基本(均值)不等式求三角形面积的最
小值.
【小问1详解】
由 ,可得 ,
令 ,所以直线 过定点 .
【小问2详解】
由(1)知,直线 恒过定点 ,由题意可设直线 的方程为 ,
设直线 与 轴, 轴正半轴交点为 , ,令 ,得 ;令 ,得 ,
所以 面积 ,
当且仅当 ,即 时, 面积最小值为4.