数学-信阳高中北湖校区2024-2025学年高二上学期开学考_2024-2025高二（7-7月题库）_2024年09月试卷_0908河南省信阳高中北湖校区2024-2025学年高二上学期开学考

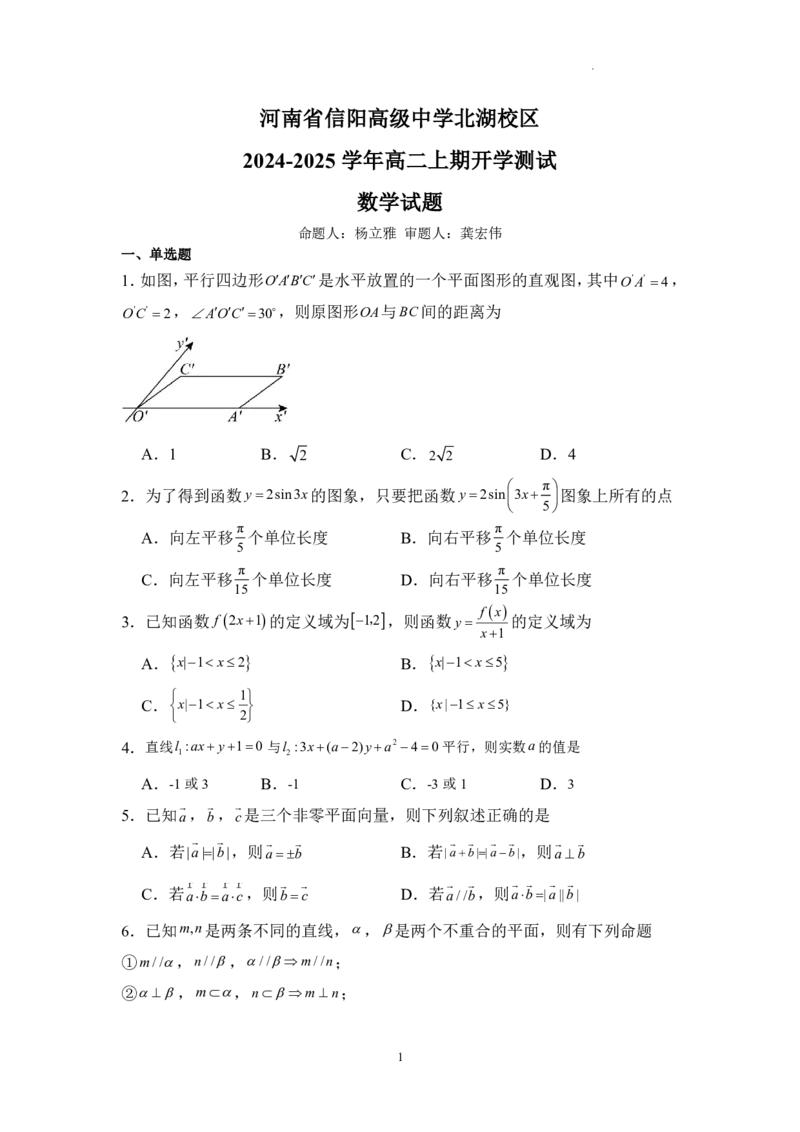
河南省信阳高级中学北湖校区 2024-2025 学年高二上期开学测试 数学试题 命题人：杨立雅 审题人：龚宏伟 一、单选题 1．如图，平行四边形OABC是水平放置的一个平面图形的直观图，其中 OA 4 ， OC 2 ，AOC30，则原图形OA与BC间的距离为 A．1 B． 2 C． 2 2 D．4  π 2．为了得到函数y2sin3x的图象，只要把函数y2sin3x  图象上所有的点  5 π π A．向左平移 个单位长度 B．向右平移 个单位长度 5 5 π π C．向左平移 个单位长度 D．向右平移 个单位长度 15 15 3．已知函数 f 2x1的定义域为1，2 ，则函数y f x 的定义域为 x1 A．x|1x2 B．x|1x5  1 C．x|1x  D．{x|1x5}  2 4．直线l :axy10 与l :3x(a2)ya240平行，则实数a的值是 1 2 A．-1或3 B．-1 C．-3或1 D．3    5．已知 a ， b ， c 是三个非零平面向量，则下列叙述正确的是           A．若|a||b|，则 ab B．若 |ab||ab| ，则 ab r r r r         C．若 abac ，则 bc D．若 a//b ，则ab|a||b| 6．已知m,n是两条不同的直线，，是两个不重合的平面，则有下列命题 ①m//，n//，//m//n； ②，m，nmn； 1 学科网（北京）股份有限公司③m//n，m，n； ④，mm. 其中正确命题的个数为 A．0 B．1 C．2 D．3 1 2 7．在三棱锥PABC 中，点M,N 分别在棱PC,PB上，且PM  PC，PN  PB， 3 3 则三棱锥PAMN和三棱锥PABC的体积之比为 1 1 2 4 A． B． C． D． 9 3 9 9 二、多选题 8．已知i为虚数单位，则 A．若复数z的共轭复数为z ，则zz  z 2  z 2 B．若x,yC，则x yi1i的充要条件是x y1 C．若复数z z ，则z ，z R 1 2 1 2 3i 3 5 D．若复数z ，则 z  2i 5 9．已知a0，b0，且ab4，则 A．a2b4 B．a1b11 C．log 2 alog 2 b2 D． 2a  4b 8 10．下列说法不正确的有 A．若两条直线2xay50与ax2y50互相平行，则实数a的值为2 B．若直线ykxb不经过第三象限，则点(k,b)在第二象限 C．过点(2,3)且在两坐标轴上的截距相等的直线l 的方程为x y5 D．已知直线kxyk10和以M(3,1)，N(3,2)为端点的线段相交，则实数k 3 1 的取值范围为k  或k  2 2 11．V ABC中，角 A ， B ，C所对的边为a，b，c，下列叙述正确的是 A．若acosBbcosA，则V ABC是等腰三角形 a b c B．若   ，则V ABC一定是等边三角形 cosA cosB cosC C．若AB，则cosAcosB 2 学科网（北京）股份有限公司 π D．若2bac，则B0,   3 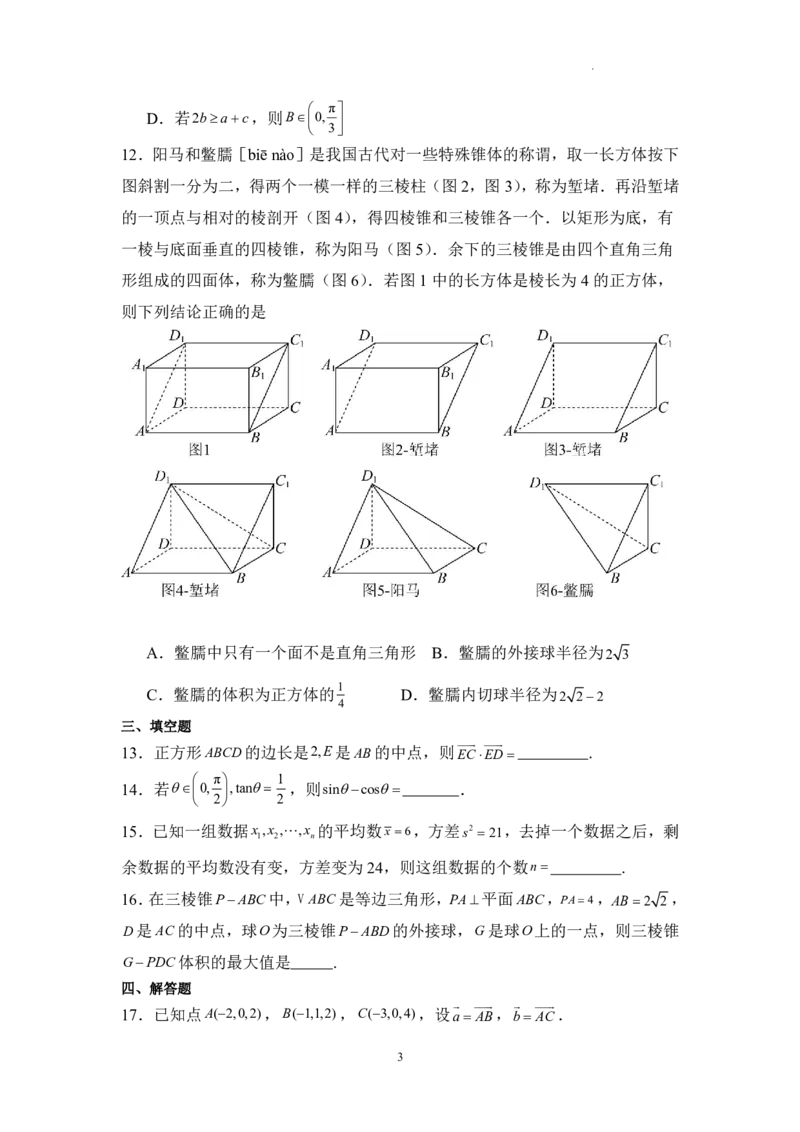12．阳马和鳖臑［biē nào］是我国古代对一些特殊锥体的称谓，取一长方体按下 图斜割一分为二，得两个一模一样的三棱柱（图2，图3），称为堑堵．再沿堑堵 的一顶点与相对的棱剖开（图4），得四棱锥和三棱锥各一个．以矩形为底，有 一棱与底面垂直的四棱锥，称为阳马（图5）．余下的三棱锥是由四个直角三角 形组成的四面体，称为鳖臑（图6）．若图1中的长方体是棱长为4的正方体， 则下列结论正确的是 A．鳖臑中只有一个面不是直角三角形 B．鳖臑的外接球半径为 2 3 1 C．鳖臑的体积为正方体的 D．鳖臑内切球半径为 2 22 4 三、填空题   13．正方形ABCD的边长是2,E是AB的中点，则 ECED .  π 1 14．若0, ,tan ，则sincos ．  2 2 15．已知一组数据x,x ,,x 的平均数x 6，方差 s2 21 ，去掉一个数据之后，剩 1 2 n 余数据的平均数没有变，方差变为24，则这组数据的个数n . 16．在三棱锥PABC中，V ABC是等边三角形，PA平面ABC， PA4 ， AB2 2 ， D是AC的中点，球O为三棱锥PABD的外接球，G是球O上的一点，则三棱锥 GPDC体积的最大值是 . 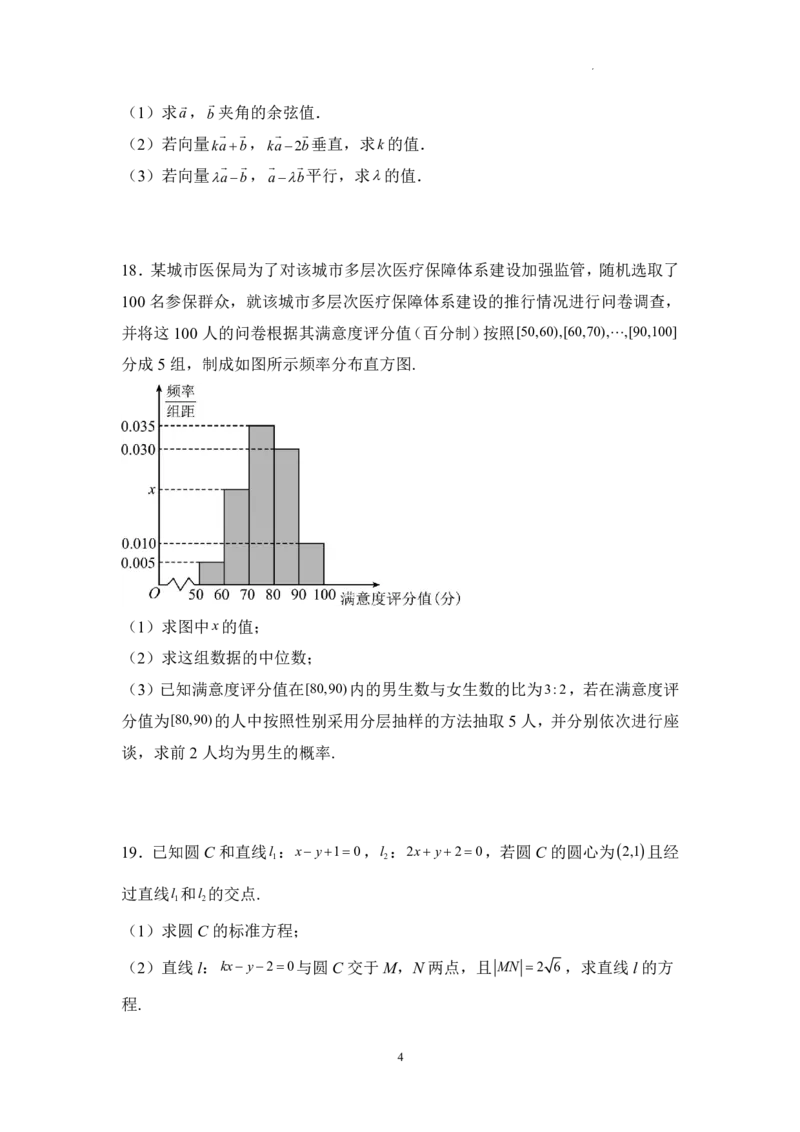四、解答题     17．已知点A(2,0,2)，B(1,1,2)，C(3,0,4)，设 a AB ， b AC ． 3 学科网（北京）股份有限公司  （1）求a， b 夹角的余弦值．     （2）若向量 kab ， ka2b 垂直，求k的值．     （3）若向量ab ， ab 平行，求的值． 18．某城市医保局为了对该城市多层次医疗保障体系建设加强监管，随机选取了 100名参保群众，就该城市多层次医疗保障体系建设的推行情况进行问卷调查， 并将这100人的问卷根据其满意度评分值（百分制）按照[50,60),[60,70),,[90,100] 分成5组，制成如图所示频率分布直方图. （1）求图中x的值； （2）求这组数据的中位数； （3）已知满意度评分值在[80,90)内的男生数与女生数的比为3:2，若在满意度评 分值为[80,90)的人中按照性别采用分层抽样的方法抽取5人，并分别依次进行座 谈，求前2人均为男生的概率. 19．已知圆C 和直线l ：xy10，l ：2x y20，若圆C的圆心为2,1且经 1 2 过直线l 和l 的交点. 1 2 （1）求圆C 的标准方程； （2）直线l：kxy20与圆C 交于M，N 两点，且 MN 2 6 ，求直线l 的方 程. 4 学科网（北京）股份有限公司B 20．在ABC中，内角A,B,C 的对边分别是a,b,c，且bsinC 3csin . 2 （1）求角 B 的大小； （2）若b6，且V ABC的面积为7 3 ，求AC边上的中线长. 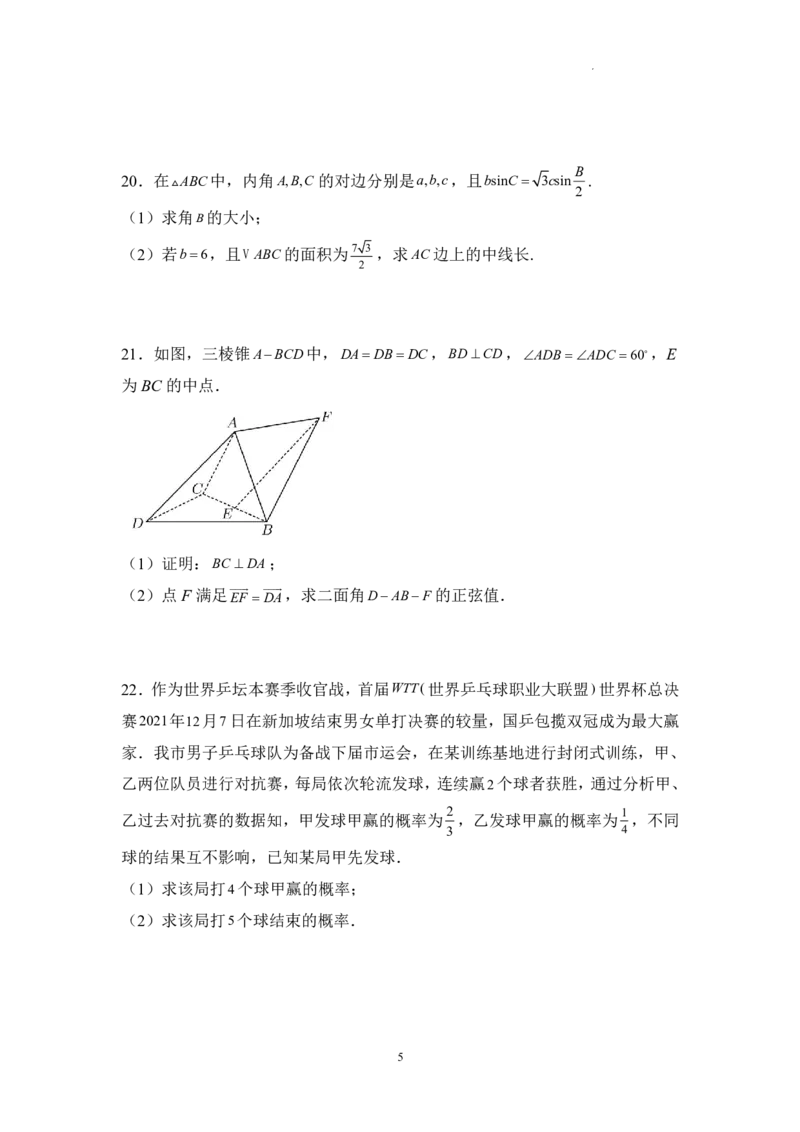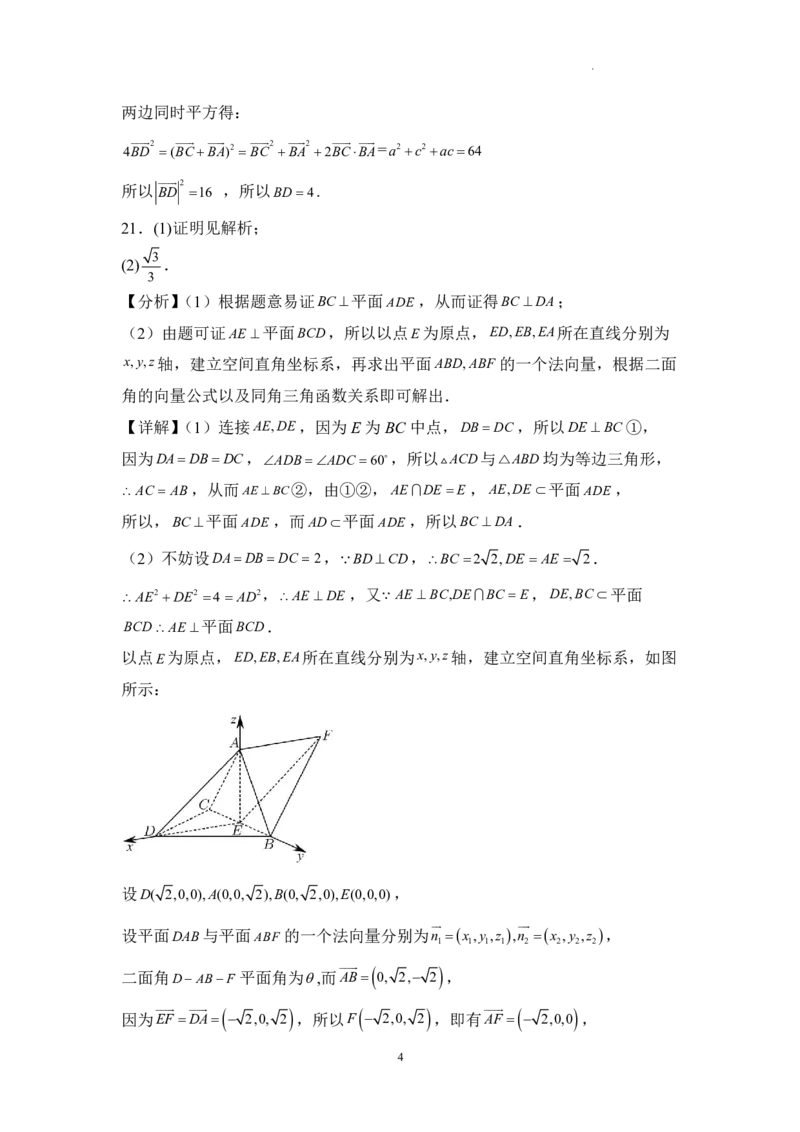2 21．如图，三棱锥ABCD中，DADBDC，BDCD，ADBADC 60，E 为BC的中点． （1）证明：BC DA；   （2）点F满足 EF DA ，求二面角DABF的正弦值． 22．作为世界乒坛本赛季收官战，首届WTT(世界乒乓球职业大联盟)世界杯总决 赛2021年12月7日在新加坡结束男女单打决赛的较量，国乒包揽双冠成为最大赢 家．我市男子乒乓球队为备战下届市运会，在某训练基地进行封闭式训练，甲、 乙两位队员进行对抗赛，每局依次轮流发球，连续赢2个球者获胜，通过分析甲、 2 1 乙过去对抗赛的数据知，甲发球甲赢的概率为 ，乙发球甲赢的概率为 ，不同 3 4 球的结果互不影响，已知某局甲先发球． （1）求该局打4个球甲赢的概率； （2）求该局打5个球结束的概率． 5 学科网（北京）股份有限公司河南省信阳高级中学北湖校区 2024-2025 学年高二上期开学测试 数学答案 题号 1 2 3 4 5 6 7 8 9 10 答案 C D B D B B C ACD AD BC 题号 11 12 答案 ABC BD 13．3 14． 5 15．8 16． 2 3 5 10 17．(1) 10 5 (2)k 2或k  . 2 (3)1 【分析】（1）利用夹角公式可求夹角的余弦值. （2）利用向量垂直的坐标形式可求参数的值. （3）利用共线向量定理可求参数的值.   【详解】（1）a1,1,0，b1,0,2，   100 10 故cos a,b   . 2 5 10 （2）由（1）可得     kabk1,k,2，ka2bk2,k,4，     因为向量 kab ， ka2b 垂直，故k2k1k280， 5 整理得到： 2k2k100 ，故k 2或k  . 2       （3）由（1）可得 a,b 不共线，故ab ， ab 均不为零向量，           若向量ab ， ab 平行，则存在非零常数t，使得abt ab ，    整理得到：tat1b 0，   t0 因为 a,b 不共线，故 ，故t1或t1， t10 故1. 1 学科网（北京）股份有限公司18．(1)0.02 540 (2) 7 3 (3) 10 【分析】（1）利用频率之和为1求解即可； （2）先判断中位数所在区间，再利用中位数的定义列式求解即可； （3）先利用分层抽样确定男女生人数，再利用列举法与古典概型的概率公式求 解即可. 【详解】（1）依题意，得0.005x0.0350.0300.01101，解得x0.02； （2）因为0.0050.02100.250.5，0.250.035100.60.5， 所以中位数在70,80间，设为m， 540 则0.25m700.0350.5，解得m . 7 （3）依题意，因为满意度评分值在 80,90的男生数与女生数的比为3:2， 按照分层抽样的方法在其中随机抽取5人，则抽中男生3人，女生2人，依次分 别记为A,A ,A,B,B ， 1 2 3 1 2 对这5人依次进行座谈，前2人的基本事件有：AA ，AA ，AB ，AB ，A A ， 1 2 1 3 1 1 1 2 2 3 A B ，AB ，AB，AB ，BB ，共 10件， 2 1 2 2 3 1 3 2 1 2 设“前2 人均为男生”为事件A，其包含的基本事件有：AA ，AA，A A ，共3 1 2 1 3 2 3 个， 3 所以PA ． 10 19．(1)x22y12 10 (2)5x12y240 【分析】（1）求出交点坐标，进而得到半径，得到圆的标准方程； （2）由垂径定理得到圆心2,1到直线kxy20的距离，利用点到直线距离公 式求出答案. 2 学科网（北京）股份有限公司xy10 x1 【详解】（1）联立 ，解得 ， 2x y20 y0 故半径为 212102  10， 故圆C 的标准方程为x22y12 10； （2）设圆心2,1到直线kxy20的距离为d， 则由垂径定理得 MN 2 10d2 2 6， 2k12 5 解得d 2，即 2，解得k  ， 1k2 12 5 故直线l的方程为 xy20，即5x12y240. 12 π 20．(1)B 3 (2)4 【分析】（1）利用正弦定理边角互化，转化为三角函数求角； （2）首先根据三角形的面积公式，求得ac14，再根据余弦定理求得 a2c2 50 ， 再根据中线向量关系， 利用数量积公式，即可求解. B B 【详解】（1）bsinC 3csin ，∴由正弦定理得：sinBsinC  3sinCsin ， 2 2 C0,π，∴sinC0， B B B B ∴sinB 3sin ，即2sin cos  3sin ， 2 2 2 2 B  π B  0,  ，∴sin 0， 2  2 2 B 3 B π ∴cos  ，  2 2 2 6 π B 3 1 1 3 7 3 （2） S  acsinB ac  ， ac14， ABC 2 2 2 2 在V ABC中，由余弦定理 b2 a2c22accosB 得 36a2c2ac，所以 a2c2 50 ，    设AC的中点为D，则 2BDBC BA ， 3 学科网（北京）股份有限公司两边同时平方得：        4BD 2 (BCBA)2 BC 2 BA 2 2BCBA=a2c2ac64  2 所以 BD 16 ，所以BD4. 21．(1)证明见解析； 3 (2) ． 3 【分析】（1）根据题意易证BC平面ADE，从而证得BC DA； （2）由题可证AE 平面BCD，所以以点E为原点，ED,EB,EA所在直线分别为 x,y,z轴，建立空间直角坐标系，再求出平面ABD,ABF 的一个法向量，根据二面 角的向量公式以及同角三角函数关系即可解出． 【详解】（1）连接AE,DE，因为E为BC 中点，DBDC，所以DEBC①， 因为DADBDC，ADBADC 60，所以 ACD与△ABD均为等边三角形， AC  AB，从而AEBC②，由①②，AEDE E ，AE,DE平面ADE， 所以，BC平面ADE，而AD平面ADE，所以BC DA． （2）不妨设DADBDC  2，BDCD，BC 2 2,DE  AE  2． AE2 DE2 4  AD2，AE DE，又AE BC,DEBC E，DE,BC平面 BCDAE 平面BCD． 以点E为原点，ED,EB,EA所在直线分别为x,y,z轴，建立空间直角坐标系，如图 所示： 设D( 2,0,0),A(0,0, 2),B(0, 2,0),E(0,0,0)，   设平面DAB与平面ABF 的一个法向量分别为n x,y,z ,n x ,y ,z ， 1 1 1 1 2 2 2 2    二面角DABF 平面角为,而AB 0, 2, 2 ，          因为EF DA  2,0, 2 ，所以F  2,0, 2 ，即有AF   2,0,0 ， 4 学科网（北京）股份有限公司  2x  2z 0   1 1 ，取x 1，所以n (1,1,1)；  2y  2z 0 1 1 1 1   2y  2z 0   2 2 ，取y 1，所以n (0,1,1)，  2x 0 2 2 2   n n 所以， cos  1  2  2  6 ，从而sin 1 6  3 ． n n 3 2 3 9 3 1 2 3 所以二面角DABF 的正弦值为 ． 3 1 19 22．(1) (2) 12 216 【分析】（1）先设甲发球甲赢为事件A，乙发球甲赢为事件B，然后分析这4个 球的发球者及输赢者，即可得到所求事件的构成，利用相互独立事件的概率计算 公式即可求解； （2）先将所求事件分成甲赢与乙赢这两个互斥事件，再分析各事件的构成，利 用互斥事件和相互独立事件的概率计算公式即可求得概率． 【详解】（1）设甲发球甲赢为事件A，乙发球甲赢为事件B，该局打4个球甲赢 为事件C， 2 1 由题知，P(A) ，P(B) ，∴ C  ABAB ， 3 4 2 3 2 1 1 ∴P(C)P(ABAB)P(A)P(B)P(A)P(B)     ， 3 4 3 4 12 1 ∴该局打4个球甲赢的概率为 ． 12 （2）设该局打5个球结束时甲赢为事件D，乙赢为事件E，打5个球结束为事 件F，易知D，E 为互斥事件， D ABABA ， E ABABA ，F DE， ∴P(D)P(ABABA)P(A)P(B)P(A)P(B)P(A)  2 1  2 1 2 1 1  1    ，  3 4  3 4 3 216 2  1 2  1  2 1 P(E)P(ABABA)P(A)P(B)P(A)P(B)P(A)  1  1 1  ， 3  4 3  4  3 12 1 1 19 ∴P(F)P(DE)P(D)P(E)   ， 216 12 216 19 ∴该局打5个球结束的概率为 ． 216 5 学科网（北京）股份有限公司