数学-浙江丽水五校高中发展共同体2024学年高二第一学期10月联考_2024-2025高二（7-7月题库）_2024年10月试卷_1022浙江丽水五校高中发展共同体2024学年高二第一学期10月联考

学年第一学期丽水五校高中发展共同体 月联考 2024 10 高二年级数学学科 试题 考生须知： 1．本卷共4 页，满分150分，考试时间120分钟。 2．答题前，在答题卷指定区域填写班级、姓名、考场号、座位号及准考证号并填涂相应数字。 3．所有答案必须写在答题纸上，写在试卷上无效。 4．考试结束后，只需上交答题纸。 选择题部分 一、选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题 目要求的. 1．已知直线l过点A(1,0),B(2, 3)，则直线l的倾斜角为（ ）   2 5 A． B． C． D． 6 3 3 6 2．已知直线l：mx y30和直线n：3m2xm2y10，则“m1”是“l∥n”的（ ） A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 3．已知a  1,2,1,b  2,2,0，则a  在b  方向上的投影向量的模长为（ ） 3 2 3 2 A． 6 B． 6 C． D． 2 2 4．圆C ：x2 y22x2y20与圆C ：x2 y24x2y10的公切线有且仅有（ ） 1 2 A．1条 B．2条 C．3条 D．4条 5．正四棱锥PABCD中，PA 2AB,E为PC的中点，则异面直线BE与AC 所成角的余弦值为（ ） 6 3 2 2 6 A． B． C． D． 6 4 4 3 6．已知点M4,2是直线l被椭圆x24y2 36所截得的线段AB的中点，则直线l的方程为（ ） A．2x y-80 B．x2y-80 C．x-2y-80 D．2x-y-80 2π 7．已知球O与正方体ABCD ABCD的各个面相切，平面ACB 截球O所得的截面的面积为 ，则正方 1 1 1 1 1 3 体棱长为（ ） 3 1 A．2 B．1 C． D． 3 2 8．关于椭圆有如下结论：“过椭圆 x2  y2 1ab0上一点Px ,y 作该椭圆的切线，切线方程为 a2 b2 0 0 高二数学学科 试题 第1页(共4页)x x y y x2 y2 0  0 1.”设椭圆C：  1ab0的左焦点为F，右顶点为A，过F且垂直于x轴的直线与C a2 b2 a2 b2 的一个交点为M，过M作椭圆的切线l，若切线l与直线AM 的倾斜角互补，则C的离心率为（ ） 3 1 2 1 A． B． C． D． 3 3 2 2 二、选择题：本题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合题目要求.全部选 对的得6分，部分选对的得部分分，有选错的得0分． 9．已知空间中三点A(0，1，0)，B(1，2，0)，C(1，3，1)，则正确的有（ ） A． AB 与 AC 是共线向量 B．点C关于 y轴的对称点的坐标是  1，3，-1  3 C． AB 与 BC 夹角的余弦值是- 6  2 2  D．与 AB 同向的单位向量是   ， ，0    2 2  10．已知线段AB是圆C:(x1)2(y3)2 4 的一条动弦，G为弦AB的中点， AB 2 3，直线 l :mxy3m10 与直线l :xmy3m10相交于点P，下列说法正确的是（ ） 1 2 A．弦AB的中点轨迹是圆 B．直线l ,l 分别过定点(0,1)和(-1,-3) 1 2 C．直线l ,l 的交点P在定圆x2 y24x2y0上 1 2 D．线段PG的最小值为4- 5 x2 y2 11.已知椭圆C：  1  a2 的左、右焦点分别为F,F ，过椭圆C上一点P和原点O作直线l交圆 a2 3 1 2 O：x2 y2 a26于M，N两点，下列结论正确的是（ ） A．实数a越小，椭圆C越圆 2 B．若PF  PF ，且 OP  PM ，则e 1 2 2 C．若 PF  PF 6，则 PM  PN 9 1 2   D．当a2时，过F 的直线l 交C于A，B两点（点A在x轴的上方）且AF 2FB，则l 的斜率k  5 1 1 1 1 1 高二数学学科 试题 第2页(共4页)非选择题部分 三、填空题：本题共3小题，每小题5分，共15分． 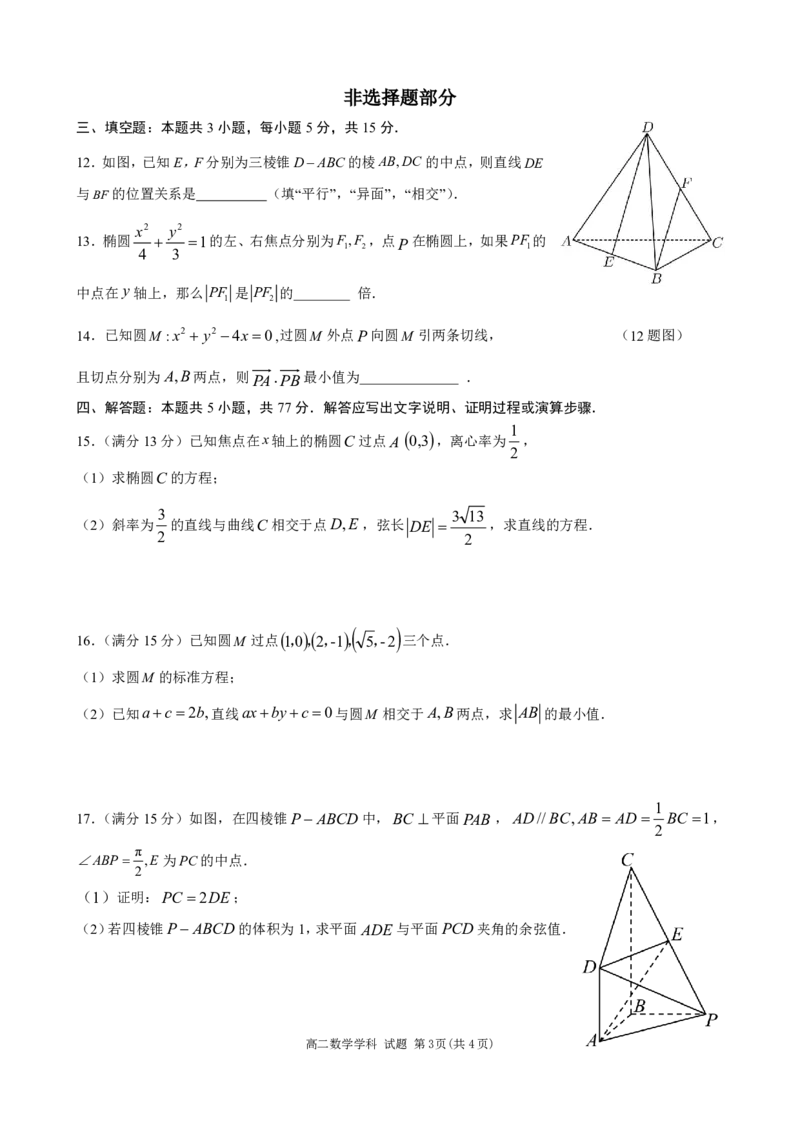12．如图，已知E，F分别为三棱锥DABC的棱AB,DC 的中点，则直线DE 与BF的位置关系是 （填“平行”，“异面”，“相交”）． x2 y2 13．椭圆  1的左、右焦点分别为F 1 ,F 2 ，点 P 在椭圆上，如果PF 1 的 4 3 中点在 y轴上，那么 PF 是 PF 的 倍． 1 2 14．已知圆M :x2  y2 4x0,过圆M 外点P向圆M 引两条切线， （12题图） 且切点分别为A,B两点，则 PAPB 最小值为 ． 四、解答题：本题共5小题，共77分．解答应写出文字说明、证明过程或演算步骤． 1   15．（满分13分）已知焦点在x轴上的椭圆C过点A 0,3 ，离心率为 ， 2 （1）求椭圆C的方程； 3 3 13 （2）斜率为 的直线与曲线C相交于点D,E，弦长 DE  ，求直线的方程． 2 2   16．（满分15分）已知圆M 过点 1，0 ， 2，-1 ，5，-2 三个点． （1）求圆M 的标准方程； （2）已知ac2b,直线axbyc0与圆M 相交于A,B两点，求 AB 的最小值． 1 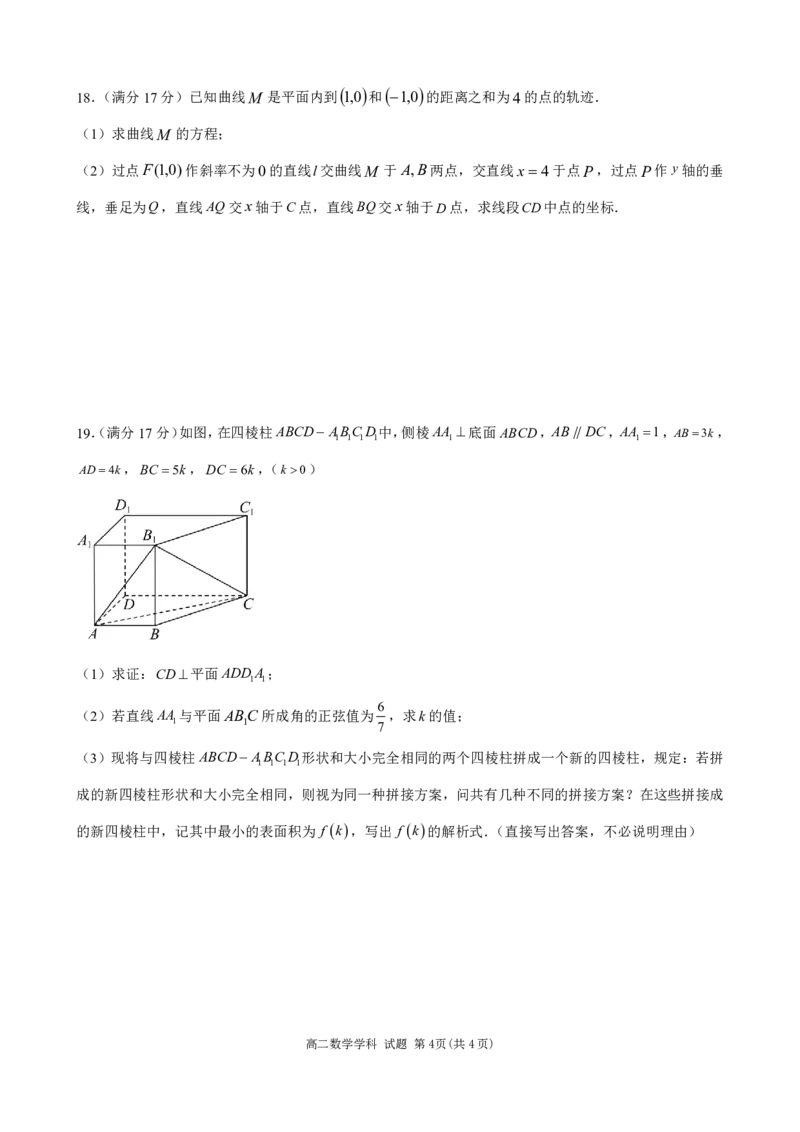17．（满分15分）如图，在四棱锥P ABCD中，BC 平面PAB ，AD//BC,AB  AD  BC 1， 2 π ABP ,E 为PC的中点． 2 （1）证明：PC 2DE； （2）若四棱锥P ABCD的体积为1，求平面ADE 与平面PCD夹角的余弦值． 高二数学学科 试题 第3页(共4页)    18．（满分17分）已知曲线M 是平面内到 1,0 和 1,0 的距离之和为4的点的轨迹． （1）求曲线M 的方程； （2）过点F(1,0)作斜率不为0的直线l交曲线M 于A,B两点，交直线x4于点P，过点P作y轴的垂 线，垂足为Q，直线AQ交x轴于C点，直线BQ交x轴于D点，求线段CD中点的坐标． 19．（满分17分）如图，在四棱柱ABCD ABCD中，侧棱AA 底面ABCD，ABDC，AA 1，AB3k， 1 1 1 1 1 1 AD4k，BC 5k，DC 6k，（k0） （1）求证：CD平面ADDA； 1 1 6 （2）若直线AA 与平面ABC所成角的正弦值为 ，求k的值； 1 1 7 （3）现将与四棱柱ABCD ABCD形状和大小完全相同的两个四棱柱拼成一个新的四棱柱，规定：若拼 1 1 1 1 成的新四棱柱形状和大小完全相同，则视为同一种拼接方案，问共有几种不同的拼接方案？在这些拼接成 的新四棱柱中，记其中最小的表面积为 f k，写出 f k的解析式．（直接写出答案，不必说明理由） 高二数学学科 试题 第4页(共4页)学年第一学期丽水五校高中发展共同体 月联考 2024 10 高二数学答案 （ 2024.10 ） 一、单项选择题 BADB CBAD 二、多项选择题 9．BCD 10． ACD 11．ABC 三、填空题 5 12．异面 13． 14. 8 2-12 3 四、解答题 b3  c 1 15.解：（1）由题意得  得c2 3,a2 12.........3分 a 2   a2 b2 c2 x2 y2 椭圆方程为  1.....................................5分 12 9 3 （2）设直线L： y  xm,D(x ,y ),E(x ,y ) 2 1 1 2 2  3 y  xm x x m   2  1 2 联立 整理得，3x2 3mxm2 90 m2 9 .....................................8分 x2 y2 x x    1  1 2 3 12 9 9 m2 9 13 36m2 3 13  DE  1k2 x x  1 m2 4( )   ..................................10分 1 2 4 3 2 3 2 解得m3符合 0 .....................................12分 3 直线l方程为y  x3,即3x2y60....................................13分 2 16.解：（1）设圆的方程为x2  y2 DxEyF 0 1DF 0  带入各点得：412DEF 0  D 0,E 4,F -1  54 5D2EF 0 所求圆的一般方程为：x2  y2 4y10 标准方程为：x2 (y2)2 5.........................................7分 （2）把c2ba代入直线方程得：axby2ba 0，所以直线过定点N  1，-2  .......................11分又 MN 1 5 ,所以定点N 在圆内，..........................12分 当MN  AB时，AB 4.........................................15分 min 17.解：（1）解法一：因为BC平面PAB，且AB，PB平面PAB， π 所以BC AB，BCPB，又ABP ，即AB PB， 2 以BA,BP,BC 分别为x轴，y轴，z轴建立如图所示的空间直角坐标系Bxyz， 1 设PBt(t 0)，由AB AD BC1，E为PC的中点， 2 t 得D1,0,1，P(0,t,0)，C0,0,2，E(0, ,1)， 2   t 所以PC(0,t,2)，DE (1, ,0)， 2   t2 t24 所以 PC  t24， DE  1 ， 4 2 所以PC 2DE.........................................6分 解法一：连接 DB,得 DB 2，CD 2,BC 2,所以CDBD,又PB AB,PBCB,ABCB B , 所以 PB 面CDB,PB CD,BDPB  B,所以CD 面PDB,所以CD  PD , CDP为直角三角形，E为斜边上中点，则有PC 2DE .................................6分 （2）由四棱锥P ABCD的体积为1解得PB2,可得A1,0,0，D1,0,1，E(0,1,1),P(0,2,0),C0,0,2，   所以AD0,0,1，AE(1,1,1)，DC 1,0,1，PC(0,2,2),DP (1,2,1)  设平面ADE的法向量为m(x，y，z)， 所以   ADm0 z 0   m(1,1,0)  AEm0 x yz 0 设平面PCD的一个法向量为na,b,c .   PDn0 x2yz 0   n(1,1,1)  PCn0 2y2z 0 mn 2 6 所以 cos m,n    ， m  n 2 3 3 6 所求角的余弦值为 .............................................15分 3 x2 y2 18.解：（1）由椭圆定义可知轨迹为椭圆，设曲线M 的方程  1 (ab0)， a2 b2 则c1,2a4,a2,a2 4,b2 413， x2 y2 曲线的M 方程  1；.............................................5分 4 3 （2）方法一：直线l的斜率存在且不为0，设直线l方程为ykx1k 0，.................................6分 x2 y2   1 联立 4 3 ，整理得 ，  ykx1 2 2 2 2 3+4 −8 +4 −12=0 64k416(34k2)(k23)144k21440， 设Ax,y ,Bx ,y ，则x x  8k2 ，xx  4k212 ，..........................................9分 1 1 2 2 1 2 34k2 1 2 34k2 直线l交直线x4于P4,3k，则Q0,3k， y 3k 所以直线AQ的方程为y 1 x3k，x 0， x 1 1 3kx  3kx  令y0，解得x 1 ，则C 1 ,0，..........................................10分 3ky 3ky  1 1 y 3k 所以直线BQ的方程为y 2 x3k，x 0， x 2 2 3kx  3kx  令y0，解得x 2 ，则D 2 ,0，..........................................11分 3ky 3ky  2 2  3kx 1  3kx 2  3k x 1 y 2 3kx 2 y 1 3k   3k x 1 kx 2 4x 2 kx 1 4  3ky 3ky y 3ky 3k k2x 4x 4 1 2 1 2 1 2 16k2 4k2 12  12x 1 x 2 6x 1 x 2  6 2 x 1 x 2 x 1 x 2  6 34k2  34k2 x 4x 4 xx 4x x 16 4k212 32k2 1 2 1 2 1 2  16 34k2 34k212k212 6 2，..........................................16分 36k236 所以线段CD中点的坐标为(1,0)...........................................17分 方法二：直线l的斜率存在且不为0，设直线l方程为myx1m0，..........................6分 x2 y2 联立   4  3 1 ，整理得  3m24  y26mx90，   myx1 36m236(3m24)0， 6m 9 设Ax,y ,Bx ,y ，则y y  ，y y  ，.........................................9分 1 1 2 2 1 2 43m2 1 2 43m2  3   3  直线l交直线x4于P4, ，则Q0, ，  m  m 3 y  所以直线AQ的方程为 1 m 3 ，x 0， y x 1 x m 1 3x  3x  令y0，解得x 1 ，则C 1 ,0，..........................................10分 3my 3my  1 1  3x  同理可得D 2 ,0，..........................................11分 3my  2  3x 1  3x 2  3 x 1 my 2 3x 2 my 1 3   3   my 1 1 my 2 3  my 2 1 my 1 3   3my 3my 3my 3my  3my 3my 1 2 1 2 1 2 9m2 6m2 6  m2y y my  y 3   3  1 2 1 2 6 43m2 43m2 m2y y 3my y 9 9m2 18m2 1 2 1 2  9 43m2 43m2 12m212 6 2，..........................................16分 36m236 所以线段CD中点的坐标为(1,0)...........................................17分 19.解：（1）证明：取DC的中点E，连接BE， AB  ED,ABED3k， 四边形ABED是平行四边形， BEPAD，且BE  AD4k，BE2EC2 （4k）2（3k）2 （5k）2 BC2， BEC 90，BECD， 又Q BEPAD，CD AD ． 侧棱AA 底面ABCD，AA CD， 1 1 ， 平面ADDA．..........................................4分 1 1 ∵ 1∩ = ∴ ⊥   （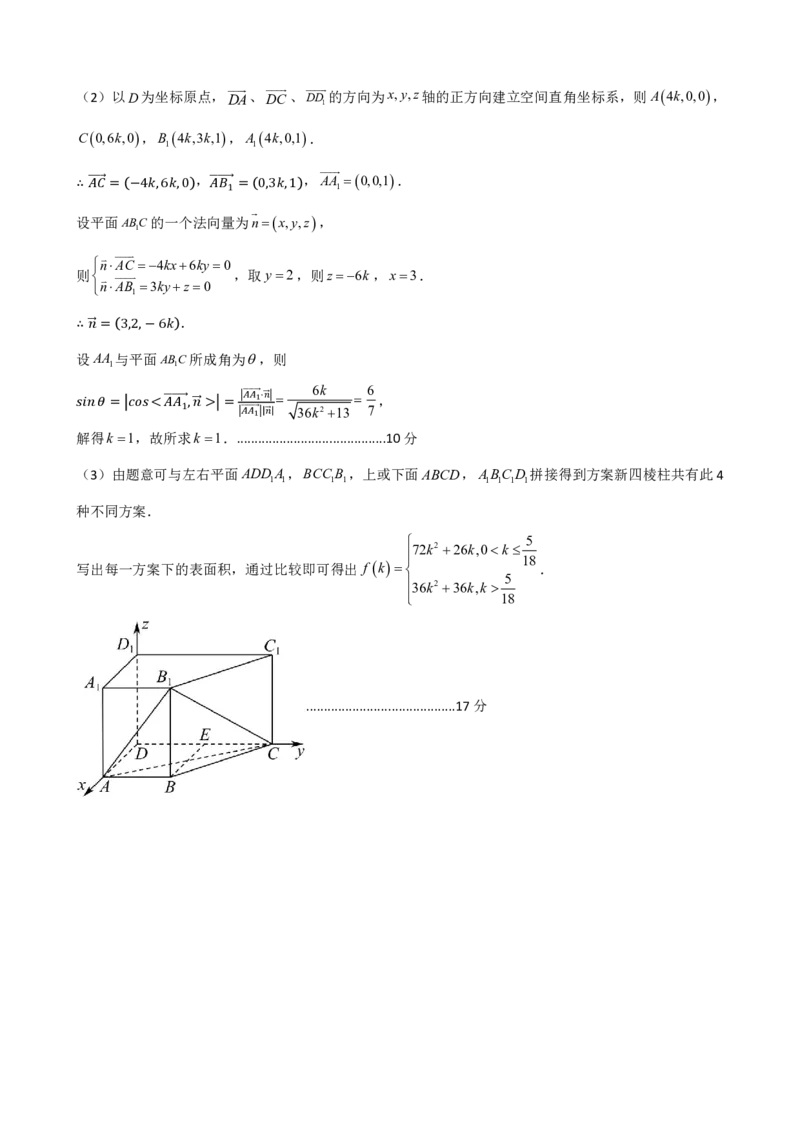2）以D为坐标原点，DA、DC、DD 的方向为x,y,z轴的正方向建立空间直角坐标系，则A4k,0,0， 1 C0,6k,0，B 4k,3k,1，A 4k,0,1． 1 1  ， ，AA 0,0,1． 1 ∴ = −4 ,6 ,0 1=0,3 ,1 设平面ABC的一个法向量为nx,y,z， 1   nAC 4kx6ky0 则  ，取y2，则z6k，x3． nAB 3kyz0 1 ． ∴ 设 A = A 与 3, 平 2, 面 −6 A BC所成角为，则 1 1 6k 6   ， 1⋅ 36k213 7 解 得 k = 1 ， 故 < 所 求 1, k  > 1． = .. . . . 1 . .. . .................................10分 （3）由题意可与左右平面ADDA，BCCB ，上或下面ABCD，ABCD 拼接得到方案新四棱柱共有此4 1 1 1 1 1 1 1 1 种不同方案．  5 72k226k,0k  写出每一方案下的表面积，通过比较即可得出 f k   18 ．  36k236k,k  5  18 ..........................................17分