2025—2026学年（上）高二级中段模块考试数学（题目）_251208广东省实验中学2025-2026学年高二上学期期中考试（全）

广东实验中学 2025—2026 学年（上）高二级中段模块考试 数 学 命题：张俊杰 审定：许作舟 校对：陈康武 本试卷分选择题和非选择题两部分，共4页，满分150分，考试用时120分钟。 注意事项： 1．答卷前，考生务必用黑色字迹的钢笔或签字笔将自己的姓名、考号填写在答题卷上。 2．选择题每小题选出答案后，用2B 铅笔把答题卷上对应题目的答案标号涂黑；如需改动， 用橡皮擦干净后，再选涂其它答案；不能答在试卷上。 3．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卷各题目指定区域内的 相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改 液.不按以上要求作答的答案无效。 4．考生必须保持答题卡的整洁，考试结束后，将答题卷收回。 第一部分 选择题 （共58分） 一、单选题：本题共8小题，每小题5分，共40分。在每小题给出的选项中，只有一项是符 合题目要求的。 1．设 z  i(2  i) ，则 z （ ）． A． 1  2i B． 1  2i C．  1  2i D． 1  2i 2．直线𝑥− 3𝑦+1=0 的倾斜角为（ ）． A．30° B．45° C．120° D．150° 3．已知圆C:x2 4x y2 0与圆D:x22 y32 r2外切，则半径r （ ）． A．2 B．3 C．4 D．5    1 4．若平面，的法向量分别为a (sin,cos,2)，b  sin,cos, ，[0,)，  2 且，则的值为（ ）．   2 3 A． B． C． D． 4 2 3 4 5．若双曲线x2  y2  1  a  0,b  0 的渐近线方程为 y   3 x ，则双曲线的离心率为（ ）． a2 b2 3 2 3 4 A． B． C．2 D．4 3 3 高二数学 第1页，共4页6．如图所示，已知正方体ABCD ABC D ，则直线C D 与平面ABC所成的角为（ ）． 1 1 1 1 1 1 1 A．30° B．45° C．60° D．90° x2 y2 7．已知椭圆C：  1 ，过点P1,1的直线l与椭圆C交于A，B两点，若点P恰为弦 4 3 AB的中点，则直线l的斜率是（ ）． 4 3 4 3 A． B． C． D． 3 4 3 4 8．已知点𝑀是圆𝑥2+𝑦2 =1 上的动点，点𝑁是圆(𝑥−5)2+(𝑦−2)2 =4 上的动点，点𝑃在直 线𝑥+𝑦+5=0 上运动，则|𝑃𝑀|+|𝑃𝑁|的最小值为（ ）． A． 29+3 B． 149+3 C． 29−3 D． 149−3 二、多选题：本题共3小题，每小题6分，共18分。在每小题选项中，有多项符合题目要求。 9．已知直线𝑙 :𝑎𝑥+𝑦−3𝑎=0，直线𝑙 :2𝑥+(𝑎−1)𝑦−6=0，则下列说法正确的有（ ）． 1 2 A.当𝑎=3 时，𝑙 与𝑙 的交点为(3,0) B.直线𝑙 恒过点(3,0) 1 2 1 1 C.若𝑙 ⊥𝑙 ，则𝑎= D.存在𝑎∈𝑅，使𝑙 ∥𝑙 1 2 3 1 2 x2 y2 1 10．已知点P是椭圆  1上一点，椭圆的左、右焦点分别为F 、F ，且cosFPF  ， 9 4 1 2 1 2 3 则下列说法正确的有（ ）． A.△𝐹 𝑃𝐹 的周长为6+2 5 B.△𝐹 𝑃𝐹 的面积为2 2 1 2 1 2 10  C.点P到x轴的距离为 D. PF·PF 2 5 1 2 11．已知圆𝑀:(𝑥+4)2+𝑦2 =4 直线𝑙:𝑥+𝑦−2=0，点𝑃在直线𝑙上运动，直线𝑃𝐴，𝑃𝐵分别 与圆𝑀相切于点𝐴，𝐵，则下列选项中正确的是（ ）． A．四边形𝑃𝐴𝑀𝐵的面积最小值为2 14 B.|𝑃𝐴|最短时，弦𝐴𝐵长为 2 7 3 C.|𝑃𝐴|最短时，弦𝐴𝐵所在直线方程为3𝑥+3𝑦+8=0 10 2 D．直线𝐴𝐵过定点 − , 3 3 高二数学 第2页，共4页第二部分 非选择题 （92分） 三、填空题：本题共3小题，每小题5分，共15分。 x2 2x2, x0, 12．若函数 f(x) 则 f(f(1)) ． 3log x, x0. 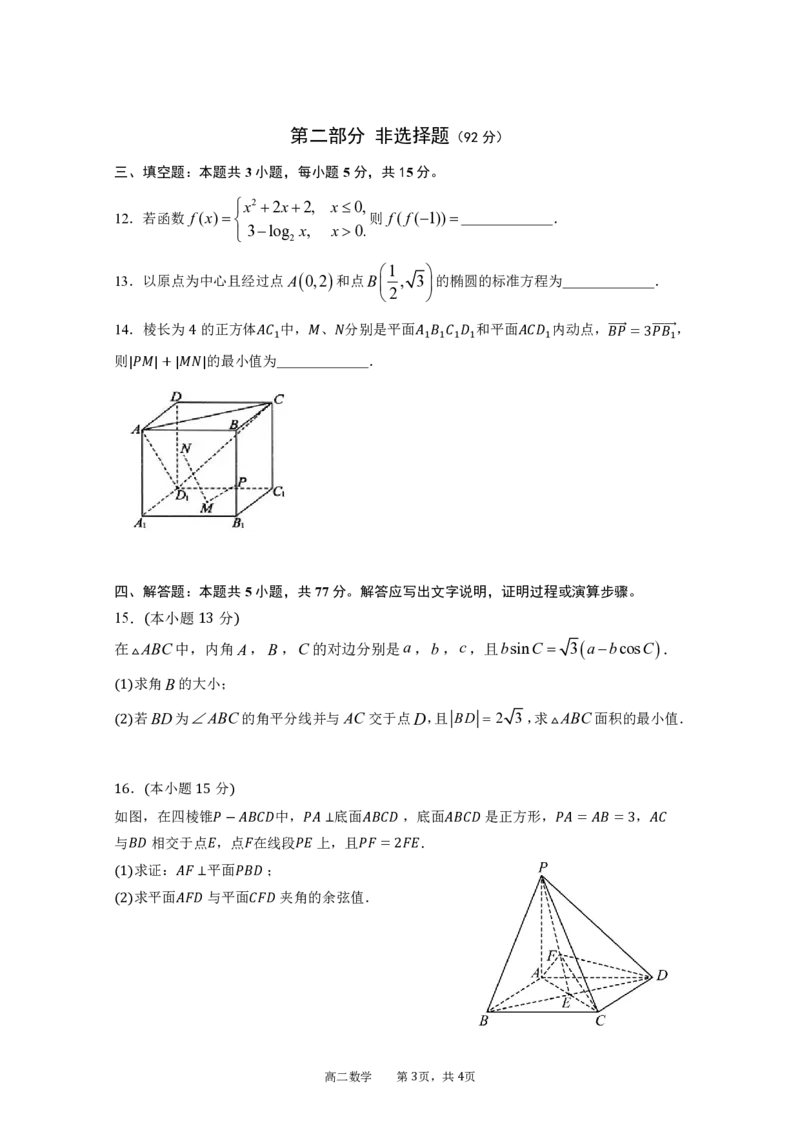 2 1  13．以原点为中心且经过点A0,2和点B  , 3 的椭圆的标准方程为 ． 2  14．棱长为4 的正方体𝐴𝐶 中，𝑀、𝑁分别是平面𝐴 𝐵 𝐶 𝐷 和平面𝐴𝐶𝐷 内动点，𝐵(cid:4652)(cid:4652)(cid:4652)𝑃(cid:4652)⃗=3𝑃(cid:4652)(cid:4652)(cid:4652)𝐵(cid:4652)(cid:4652)⃗， 1 1 1 1 1 1 1 则|𝑃𝑀|+|𝑀𝑁|的最小值为 ． 四、解答题：本题共5小题，共77分。解答应写出文字说明，证明过程或演算步骤。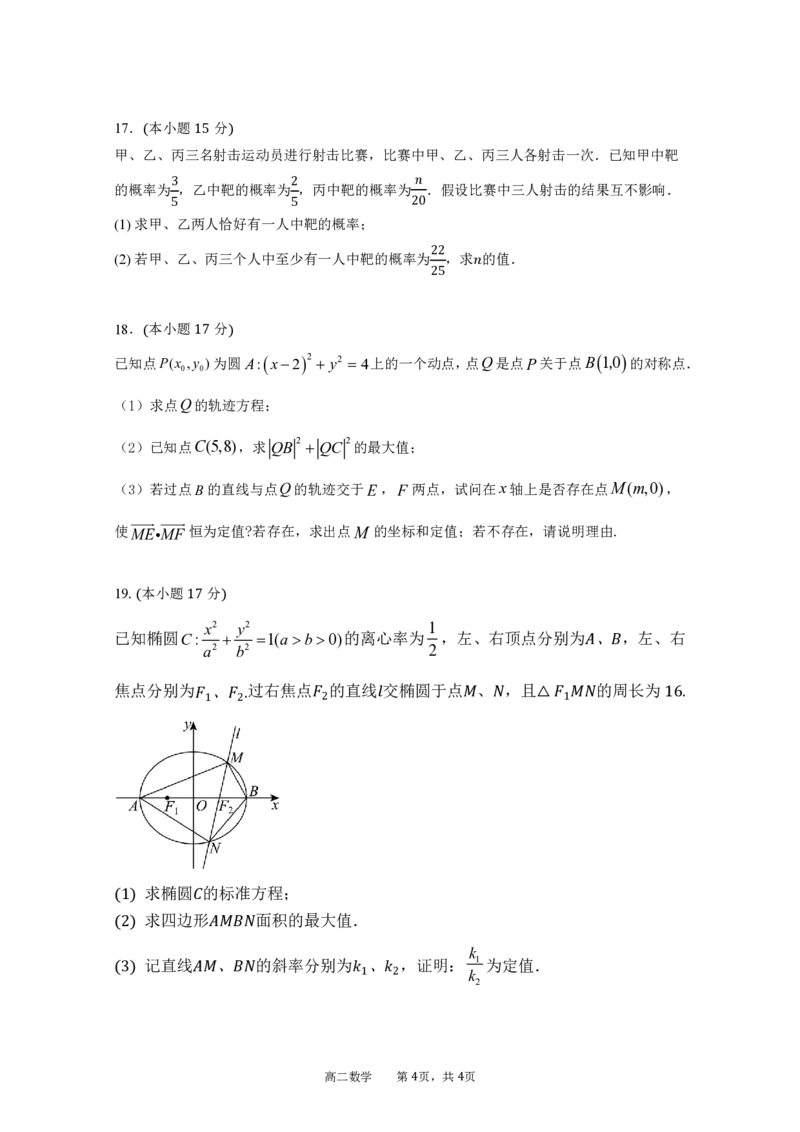 15．(本小题13 分) 在 ABC中，内角A，B，C的对边分别是a，b，c，且bsinC  3abcosC．  (1)求角B的大小； (2)若BD为ABC的角平分线并与AC交于点D，且 BD  2 3 ，求 ABC面积的最小值．  16．(本小题15 分) 如图，在四棱锥𝑃−𝐴𝐵𝐶𝐷中，𝑃𝐴⊥底面𝐴𝐵𝐶𝐷，底面𝐴𝐵𝐶𝐷是正方形，𝑃𝐴=𝐴𝐵 =3，𝐴𝐶 与𝐵𝐷相交于点𝐸，点𝐹在线段𝑃𝐸上，且𝑃𝐹=2𝐹𝐸． (1)求证：𝐴𝐹 ⊥平面𝑃𝐵𝐷； (2)求平面𝐴𝐹𝐷与平面𝐶𝐹𝐷夹角的余弦值． 高二数学 第3页，共4页17．(本小题15 分) 甲、乙、丙三名射击运动员进行射击比赛，比赛中甲、乙、丙三人各射击一次．已知甲中靶 3 2 𝑛 的概率为 ，乙中靶的概率为 ，丙中靶的概率为 ．假设比赛中三人射击的结果互不影响． 5 5 20 (1)求甲、乙两人恰好有一人中靶的概率； 22 (2)若甲、乙、丙三个人中至少有一人中靶的概率为 ，求𝑛的值． 25 18．(本小题17 分) 已知点P(x ,y )为圆A:x22  y2  4上的一个动点，点Q是点P关于点B1,0 的对称点． 0 0 （1）求点Q的轨迹方程； （2）已知点C(5,8)，求 QB 2  QC 2 的最大值； （3）若过点B的直线与点Q的轨迹交于E，F 两点，试问在x轴上是否存在点M(m,0)，   使ME MF 恒为定值?若存在，求出点M 的坐标和定值；若不存在，请说明理由.  19.(本小题17 分) x2 y2 1 已知椭圆C:  1(ab0)的离心率为 ，左、右顶点分别为𝐴、𝐵，左、右 a2 b2 2 焦点分别为𝐹 、𝐹 .过右焦点𝐹 的直线𝑙交椭圆于点𝑀、𝑁，且△𝐹 𝑀𝑁的周长为16. 1 2 2 1 (1) 求椭圆𝐶的标准方程； (2) 求四边形𝐴𝑀𝐵𝑁面积的最大值． k (3) 记直线𝐴𝑀、𝐵𝑁的斜率分别为𝑘 、𝑘 ，证明： 1 为定值． 1 2 k 2 高二数学 第4页，共4页