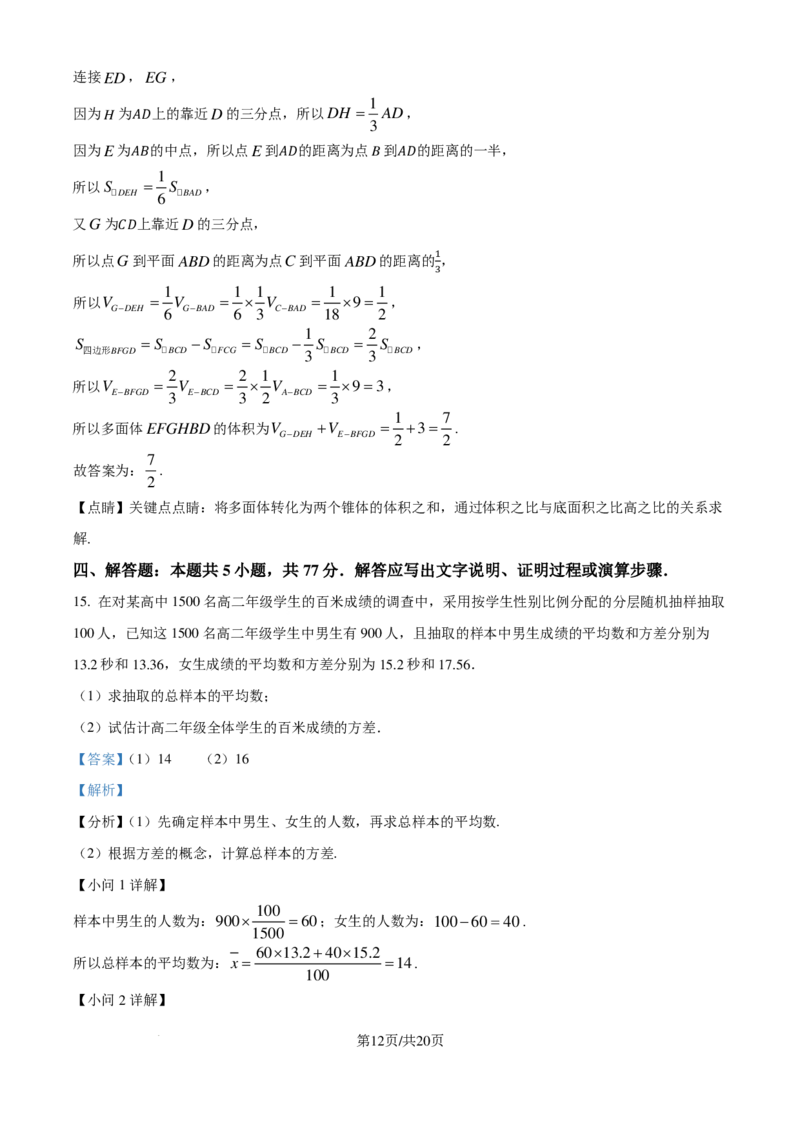文档内容
2024 年湖北云学名校联盟高二年级 10 月联考
数学试卷
命题学校:武汉二中 命题人:李凯丰 陈莉 张鹄 审题人:夷陵中学 王方 杨晓璐
考试时间:2024年 10月 15日 15:00-17:00 时长:120分钟 满分:150分
一、选择题:本题共 8小题,每小题 5分,共 40分.在每小题给出的四个选项中,只有一项
是符合题目要求的.
3+i2025
1. 已知i为虚数单位, 1+i 的虚部为( )
A. −i B. i C. −1 D. 1
2. 已知一组数据:2,5,7,x,10的平均数为6,则该组数据的第60百分位数为( )
A. 7 B. 6.5 C. 6 D. 5.5
3. 直线l :ax− y+2025=0,l : ( 3a−2 ) x+ay−2a=0,若l ⊥l ,则实数a的值为( )
1 2 1 2
1
A. 0 B. 1 C. 0或1 D. 或1
3
4. 为了测量河对岸一古树高度AB的问题(如图),某同学选取与树底B在同一水平面内的两个观测点C
与D,测得∠BCD=15°,∠BDC =30°,CD = 48m,并在点C处测得树顶A的仰角为60°,则树高
AB约为( )(取 2 ≈1.4, 3≈1.7)
A. 100.8m B. 33.6m C. 81.6m D. 57.12m
5. 如果直线ax+by=4与圆x2+y2=4有两个不同的交点,那么点P(a,b)与圆的位置关系是( )
A. P在圆外
B. P在圆上
C. P在圆内
D. P与圆的位置关系不确定
2
6. 在棱长为6的正四面体ABCD中,点P与Q满足AP= AB,且CD=2CQ,则 PQ 的值为( )
3
第1页/共4页
学科网(北京)股份有限公司A. 13 B. 15 C. 17 D. 19
7. 下列命题中正确的是( )
A. 4z2 +z2 =0,则z = z =0;
1 2 1 2
B. 若点P、Q、R、S共面,点P、Q、R、T 共面,则点P、Q、R、S、T 共面;
C. 若P
(
A
)+P (
B
)=1,则事件A与事件B是对立事件;
3
D. 从长度为1,3,5,7,9的5条线段中任取3条,则这三条线段能构成一个三角形的概率为 ;
10
8. 动点Q在棱长为3的正方体ABCD− ABC D 侧面BCC B 上,满足 QA =2 QB ,则点Q的轨迹长
1 1 1 1 1 1
度为( )
4π 3π
A. 2π B. C. 3π D.
3 2
二、选择题:本题共 3小题,每小题 6分,共 18分.在每小题给出的选项中,有多项符合题
目要求.全部选对的得 6分,部分选对的得部分分,有选错的得 0分.
9. 在平面直角坐标系中,下列说法正确的是( )
A. 若两条直线垂直,则这两条直线的斜率的乘积为−1;
2 1
B. 已知A(2,4),B ( 1,1 ) ,若直线l:kx+ y+k−2=0与线段AB有公共点,则k∈ − , ;
3 2
C. 过点 ( 1,2 ) ,且在两坐标轴上截距互为相反数的直线l的方程为x− y+1=0;
D. 若圆( x−1 )2 + y2 =4上恰有3个点到直线y = x+b的距离等于1,则b=−1± 2.
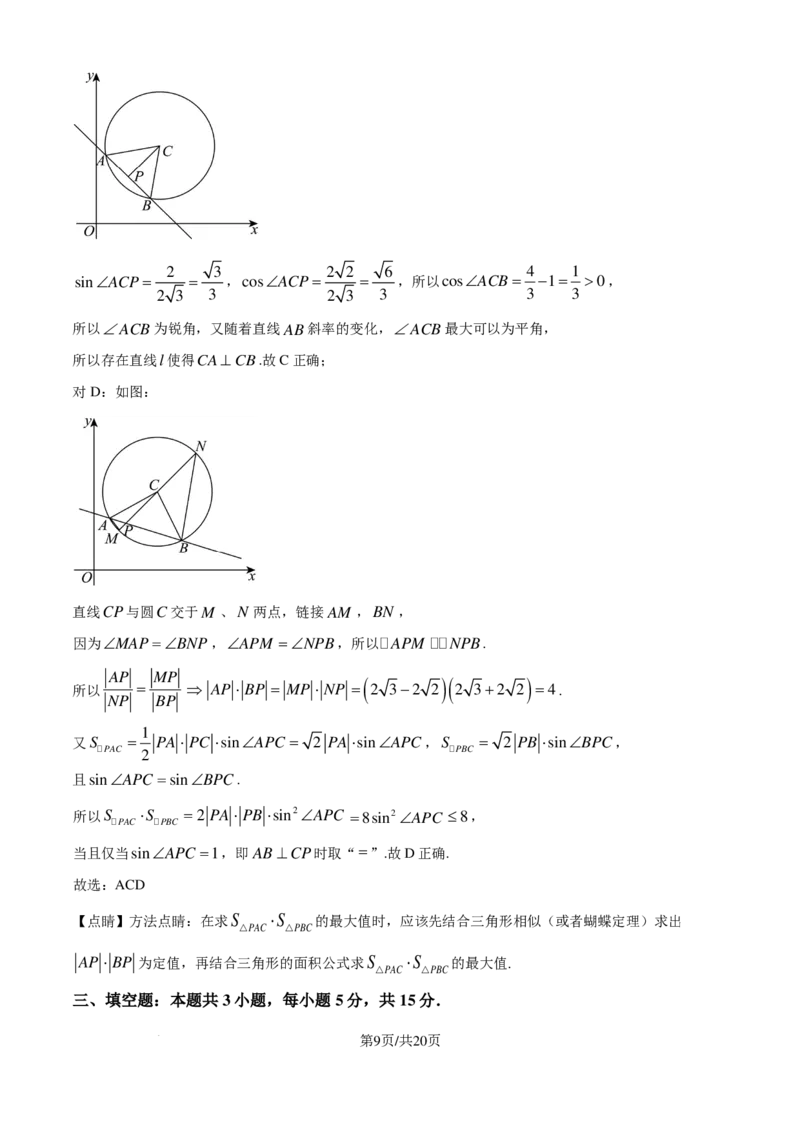
10. 如图所示四面体OABC中,OB=OC =4,OA=3,OB⊥OC,且∠AOB=∠AOC =60°,
2
CD= CB,G为AD的中点,点H 是线段OA上动点,则下列说法正确的是( )
3
1( )
A. OG = OA+OB+OC ;
3
B. 当H 是靠近A的三等分点时,DH ,OC, AB 共面;
第2页/共4页
学科网(北京)股份有限公司 5
C. 当OH = OA时,GH ⊥OA;
6
D. DH⋅OH 的最小值为−1.
11. 已知P ( 2,3 ) 是圆C:x2 + y2 −8x−10y−a+41=0内一点,其中a>0,经过点P的动直线l与C
交于A,B两点,若 的最小值为4,则( )
A. a=12; |𝐴𝐴𝐴𝐴|
B. 若 ,则直线l的倾斜角为120°;
C. 存|在𝐴𝐴𝐴𝐴直|线=l4使得CA⊥CB;
D. 记PAC与△PBC的面积分别为S ,S ,则S ⋅S 的最大值为8.
PAC PBC △PAC △PBC
三、填空题:本题共 3小题,每小题 5分,共 15分.
12. 实数x、 y满足x2 + y2 =4,则( x−4 )2 +( y+3 )2的最大值是______.
13. 记ABC的三个内角A,B,C的对边分别为a,b,c,已知acosB=( 2c−b ) cosA,其中
π 2 21
B ≠ ,若ABC的面积S =2 3,BE =2EC,且 AE = ,则BC的长为______.
2 3
14. 如图,已知四面体ABCD的体积为9,E,F 分别为AB,BC的中点,G、H 分别在CD、AD
上,且G、H 是靠近D的三等分点,则多面体EFGHBD的体积为______.
四、解答题:本题共 5小题,共 77分.解答应写出文字说明、证明过程或演算步骤.
15. 在对某高中1500名高二年级学生的百米成绩的调查中,采用按学生性别比例分配的分层随机抽样抽取
100人,已知这1500名高二年级学生中男生有900人,且抽取的样本中男生成绩的平均数和方差分别为
13.2秒和13.36,女生成绩的平均数和方差分别为15.2秒和17.56.
(1)求抽取的总样本的平均数;
(2)试估计高二年级全体学生的百米成绩的方差.
16. 在平面直角坐标系xOy中,ABC的顶点A的坐标为
(−4,2 )
,∠ACB的角平分线所在的直线方程
为x− y+1=0,AC边上中线BM 所在的直线方程为2x+ y−2=0.
第3页/共4页
学科网(北京)股份有限公司(1)求点C的坐标;
(2)求直线BC的方程.
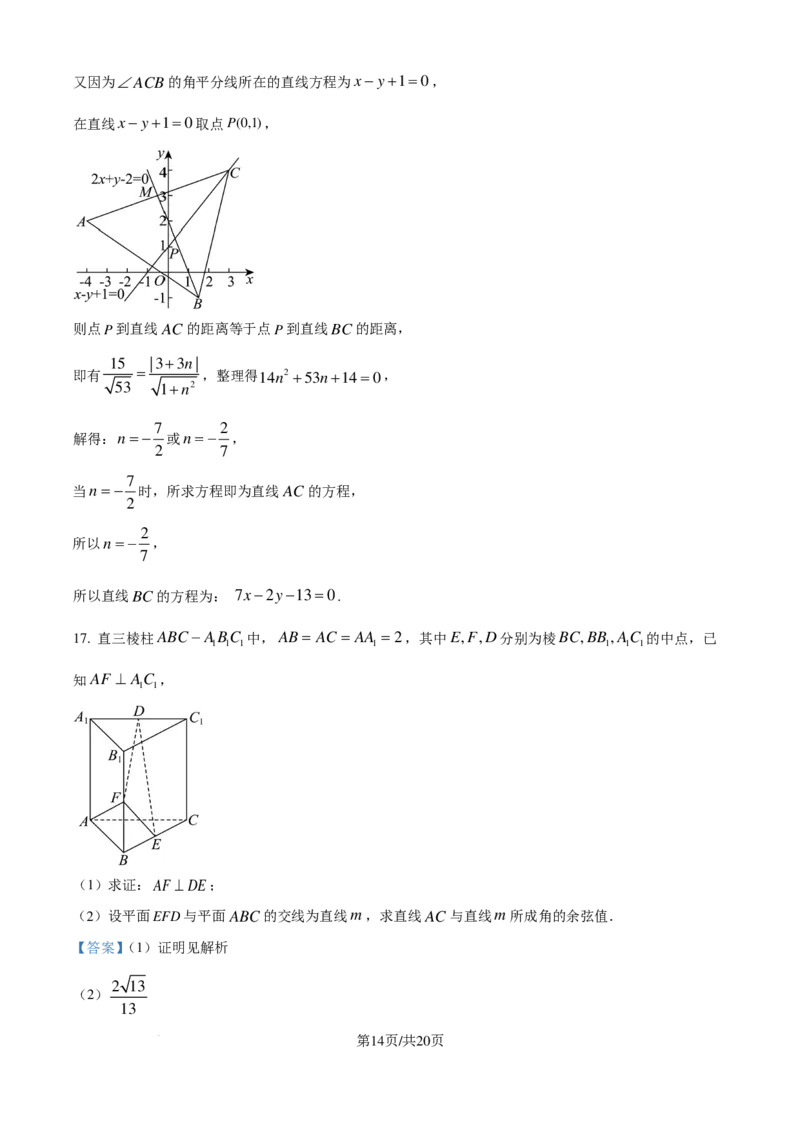
17. 直三棱柱ABC−ABC 中,AB= AC = AA =2,其中E,F,D分别为棱BC,BB,AC 的中点,已
1 1 1 1 1 1 1
知AF ⊥ AC ,
1 1
(1)求证:AF ⊥DE;
(2)设平面EFD与平面ABC的交线为直线m,求直线AC与直线m所成角的余弦值.
1
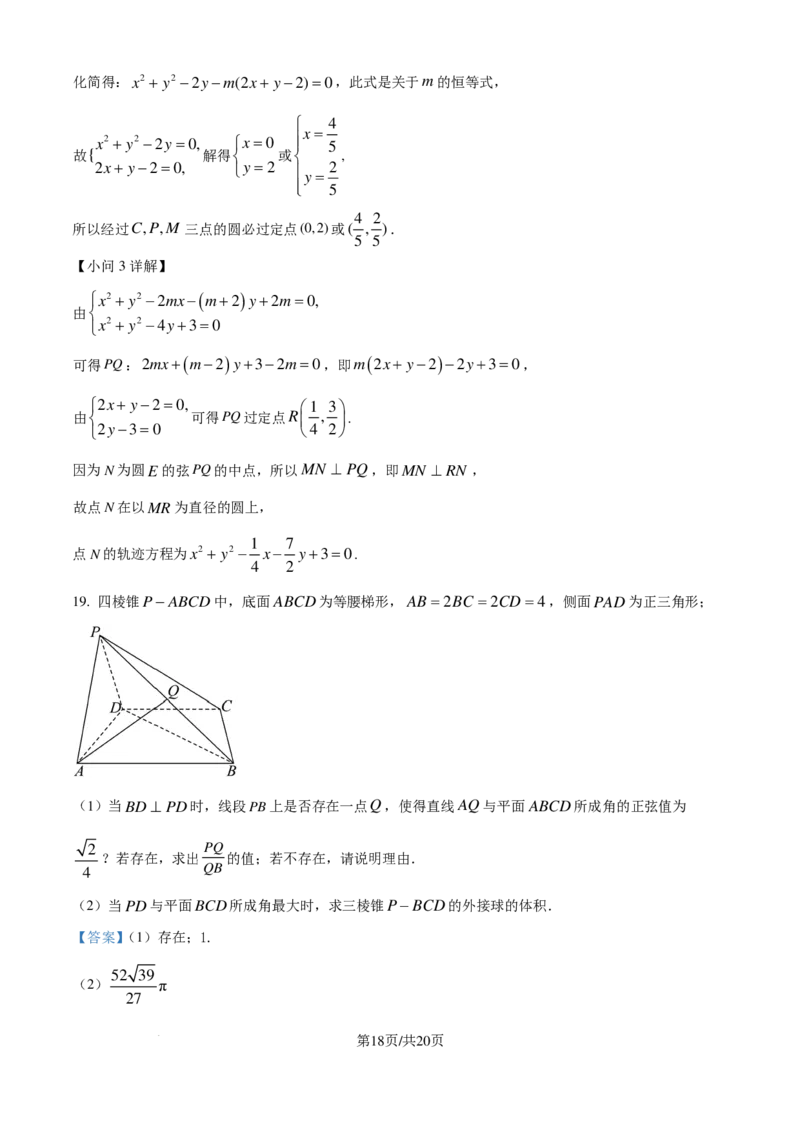
18. 已知圆C:x2 + y2 −4y+3=0,过直线l: y = x上的动点M 作圆C的切线,切点分别为P,
2
Q.
π
(1)当∠PMQ= 时,求出点M 的坐标;
3
(2)经过M ,P,C三点的圆是否过定点?若是,求出所有定点的坐标;
(3)求线段PQ的中点N 的轨迹方程.
19. 四棱锥P−ABCD中,底面ABCD为等腰梯形,AB =2BC =2CD =4,侧面PAD为正三角形;
(1)当BD⊥ PD时,线段PB上是否存在一点Q,使得直线AQ与平面ABCD所成角的正弦值为
2 PQ
?若存在,求出 的值;若不存在,请说明理由.
4 QB
(2)当PD与平面BCD所成角最大时,求三棱锥P−BCD的外接球的体积.
第4页/共4页
学科网(北京)股份有限公司2024 年湖北云学名校联盟高二年级 10 月联考
数学试卷
命题学校:武汉二中 命题人:李凯丰 陈莉 张鹄 审题人:夷陵中学 王方 杨晓璐
考试时间:2024年 10月 15日 15:00-17:00 时长:120分钟 满分:150分
一、选择题:本题共 8小题,每小题 5分,共 40分.在每小题给出的四个选项中,只有一项
是符合题目要求的.
3+i2025
1. 已知i为虚数单位, 1+i 的虚部为( )
A. −i B. i C. −1 D. 1
【答案】C
【解析】
【分析】根据复数乘方、乘法、除法运算法则结合复数的概念运算即可得出结果.
( )506
【详解】根据复数的乘方可知i2025 = i4 ⋅i=i,
3+i2025 3+i ( 3+i )( 1−i ) 3−2i+1
则 = = = =2−i,其虚部为−1.
1+i 1+i ( 1+i )( 1−i ) 2
故选:C
2. 已知一组数据:2,5,7,x,10的平均数为6,则该组数据的第60百分位数为( )
A. 7 B. 6.5 C. 6 D. 5.5
【答案】B
【解析】
【分析】先根据平均数求x的值,然后将数据从小到大排列,根据百分位数的概念求值.
2+5+7+x+10
【详解】因为 =6 ⇒ x=6.
5
所以数据为:2,5,6,7,10.
6+7
又因为5×60%=3,所以这组数据的第60百分位数为: =6.5.
2
故选:B
3. 直线l :ax− y+2025=0,l : ( 3a−2 ) x+ay−2a=0,若l ⊥l ,则实数a的值为( )
1 2 1 2
1
A. 0 B. 1 C. 0或1 D. 或1
3
【答案】C
第1页/共20页
学科网(北京)股份有限公司【解析】
【分析】根据两直线垂直的公式AA +BB =0求解即可.
1 2 1 2
【详解】因为l :ax− y+2025=0,l : ( 3a−2 ) x+ay−2a =0垂直,
1 2
所以a ( 3a−2 )+(−1 ) a=0,
解得a =0或a =1,
将a =0,a =1代入方程,均满足题意,
所以当a =0或a =1时,l ⊥l .
1 2
故选:C.
4. 为了测量河对岸一古树高度AB的问题(如图),某同学选取与树底B在同一水平面内的两个观测点C
与D,测得∠BCD=15°,∠BDC =30°,CD = 48m,并在点C处测得树顶A的仰角为60°,则树高
AB约为( )(取 2 ≈1.4, 3≈1.7)
A. 100.8m B. 33.6m C. 81.6m D. 57.12m
【答案】D
【解析】
【分析】先在△BCD中,利用正弦定理求出BC,再在Rt△ABC中求AB即可.
【详解】在△BCD中,∠BCD=15°,∠BDC =30°,所以∠CBD=135°,又CD =48,
48 CB
CD CB =
由正弦定理得: = ⇒ 2 1 ⇒ CB=24 2.
sin∠CBD sin∠CDB
2 2
在Rt△ABC中,AB= BCtan60° =24 6 ≈24×1.4×1.7 =57.12.
故选:D
5. 如果直线ax+by=4与圆x2+y2=4有两个不同的交点,那么点P(a,b)与圆的位置关系是( )
A. P在圆外
B. P在圆上
第2页/共20页
学科网(北京)股份有限公司C. P在圆内
D. P与圆的位置关系不确定
【答案】A
【解析】
−4
【详解】试题分析:由题意得 2∴a2 +b2 4,所以点 ( a,b ) 在圆外
a2 +b2
考点:1.直线与圆的位置关系;2.点与圆的位置关系
2
6. 在棱长为6的正四面体ABCD中,点P与Q满足AP= AB,且CD=2CQ,则 PQ 的值为( )
3
A. 13 B. 15 C. 17 D. 19
【答案】D
【解析】
{ }
【分析】以 AB,AC,AD 为基底,表示出PQ,利用空间向量的数量积求模.
【详解】如图:
{ }
以 AB,AC,AD 为基底,则 AB = AC = AD =6,∠BAC =∠BAD=∠CAD=60°,
所以AB⋅AC = AB⋅AD= AC⋅AD=6×6×cos60°=18.
1( ) 2 2 1 1
因为PQ= AQ−AP= AC+ AD − AB =− AB+ AC+ AD.
2 3 3 2 2
2
2 2 1 1
所以 PQ = − AB+ AC+ AD
3 2 2
4 2 1 2 1 2 2 2 1
= AB + AC + AD − AB⋅AC− AB⋅AD+ AC⋅AD
9 4 4 3 3 2
=16+9+9−12−12+9 =19.
所以 PQ = 19.
故选:D
7. 下列命题中正确的是( )
第3页/共20页
学科网(北京)股份有限公司A. 4z2 +z2 =0,则z = z =0;
1 2 1 2
B. 若点P、Q、R、S共面,点P、Q、R、T 共面,则点P、Q、R、S、T 共面;
C. 若P
(
A
)+P (
B
)=1,则事件A与事件B是对立事件;
3
D. 从长度为1,3,5,7,9的5条线段中任取3条,则这三条线段能构成一个三角形的概率为 ;
10
【答案】D
【解析】
【分析】举反例说明ABC不成立,根据古典概型的算法判断D是正确的.
【详解】对A:若z =i,z =2,则4z2 +z2 =0,但z = z =0不成立,故A错误;
1 2 1 2 1 2
对B:如图:
四面体S−PRT 中,Q是棱PR上一点,
则点P、Q、R、S共面,点P、Q、R、T 共面,但点P、Q、R、S、T 不共面,故B错误;
对C:掷1枚骰子,即事件A:点数为奇数,事件B:点数不大于3,
1 1
则P ( A )= ,P ( B )= ,P ( A )+P ( B )=1,但事件A、B不互斥,也不对立,故C错误;
2 2
对D:从长度为1,3,5,7,9的5条线段中任取3条,有C3 =10种选法,
5
{ } { } { }
这三条线段能构成一个三角形的的选法有: 3,5,7 , 3,7,9 , 5,7,9 共3种,
3
所以条线段能构成一个三角形的的概率为:P= ,故D正确.
10
故选:D
8. 动点Q在棱长为3的正方体ABCD− ABC D 侧面BCC B 上,满足 QA =2 QB ,则点Q的轨迹长
1 1 1 1 1 1
度为( )
4π 3π
A. 2π B. C. 3π D.
3 2
第4页/共20页
学科网(北京)股份有限公司【答案】D
【解析】
【分析】结合图形,计算出|BQ|= 3,由点Q∈平面BCC B ,得出点Q的轨迹为圆弧E QF ,利用弧长
1 1
公式计算即得.
【详解】
如图,易得AB⊥平面BCC B ,因BQ⊂平面BCC B ,则AB⊥ BQ,
1 1 1 1
不妨设|BQ|= r,则|AQ|=2r, |AB|= (2r)2 −r2 = 3r =3,解得r = 3,
又点Q∈平面BCC B ,故点Q的轨迹为以点B为圆心,半径为 3的圆弧E QF ,
1 1
π 3π
故其长度为 × 3 = .
2 2
故选:D.
二、选择题:本题共 3小题,每小题 6分,共 18分.在每小题给出的选项中,有多项符合题
目要求.全部选对的得 6分,部分选对的得部分分,有选错的得 0分.
9. 在平面直角坐标系中,下列说法正确的是( )
A. 若两条直线垂直,则这两条直线的斜率的乘积为−1;
2 1
B. 已知A(2,4),B ( 1,1 ) ,若直线l:kx+ y+k−2=0与线段AB有公共点,则k∈ − , ;
3 2
C. 过点 ( 1,2 ) ,且在两坐标轴上截距互为相反数的直线l的方程为x− y+1=0;
D. 若圆( x−1 )2 + y2 =4上恰有3个点到直线y = x+b的距离等于1,则b=−1± 2.
【答案】BD
【解析】
【分析】根据直线是否存在斜率判断 A的真假;数形结合求k的取值范围判断B的真假;根据截距的概念
判断真假;转化为点(圆心)到直线的距离求b判断D的真假.
【详解】对A:“若两条直线垂直,则这两条直线的斜率的乘积为−1”成立的前提是两条直线的斜率都存
第5页/共20页
学科网(北京)股份有限公司在且不为0,
若两条直线1条不存在斜率,另一条斜率为0,它们也垂直.故A是错误的.
对B:如图:
对直线l:kx+ y+k−2=0 ⇒ y−2=−k ( x+1 ) ,表示过点P (−1,2 ) ,且斜率为−k的直线,
4−2 2 1−2 1
且k = = ,k = =− ,
AP 2−(−1 ) 3 BP 1−(−1 ) 2
2 1 2 1
由直线l与线段AB有公共点,所以:0≤−k ≤ 或− ≤−k <0,即− ≤k ≤0或00,经过点P的动直线l与C
交于A,B两点,若 的最小值为4,则( )
A. a=12; |𝐴𝐴𝐴𝐴|
B. 若 ,则直线l的倾斜角为120°;
C. 存|在𝐴𝐴𝐴𝐴直|线=l4使得CA⊥CB;
D. 记PAC与△PBC的面积分别为S ,S ,则S ⋅S 的最大值为8.
PAC PBC △PAC △PBC
【答案】ACD
【解析】
【分析】根据点P ( 2,3 ) 在圆内,列不等式,可求a的取值范围,在根据弦 的最小值为4求a的值,判
|𝐴𝐴𝐴𝐴|
断 A 的真假;明确圆的圆心和半径,根据k ⋅k =−1,可求直线AB的斜率,进而求直线AB的倾斜角,
l CP
判断B的真假;利用圆心到直线的距离,确定弦长的取值范围,可判断C的真假;由三角形面积公式和相
交弦定理,可求S ⋅S 的最大值,判断D的真假.
△PAC △PBC
【详解】对A:由22 +32 −8×2−10×3−a+41<0 ⇒ a>8.
此时圆C:( x−4 )2 +( y−5 )2 =a.
因为过P点的弦 的最小值为4,所以 CP = a−4,
|𝐴𝐴𝐴𝐴|
又 CP = ( 4−2 )2 +( 5−3 )2 =2 2,由 a−4 =2 2 ⇒ a=12.故A正确;
5−3
对B:因为k = =1,k ⋅k =−1,所以直线l的斜率为−1,其倾斜角为135°,故B错误;
CP 4−2 l CP
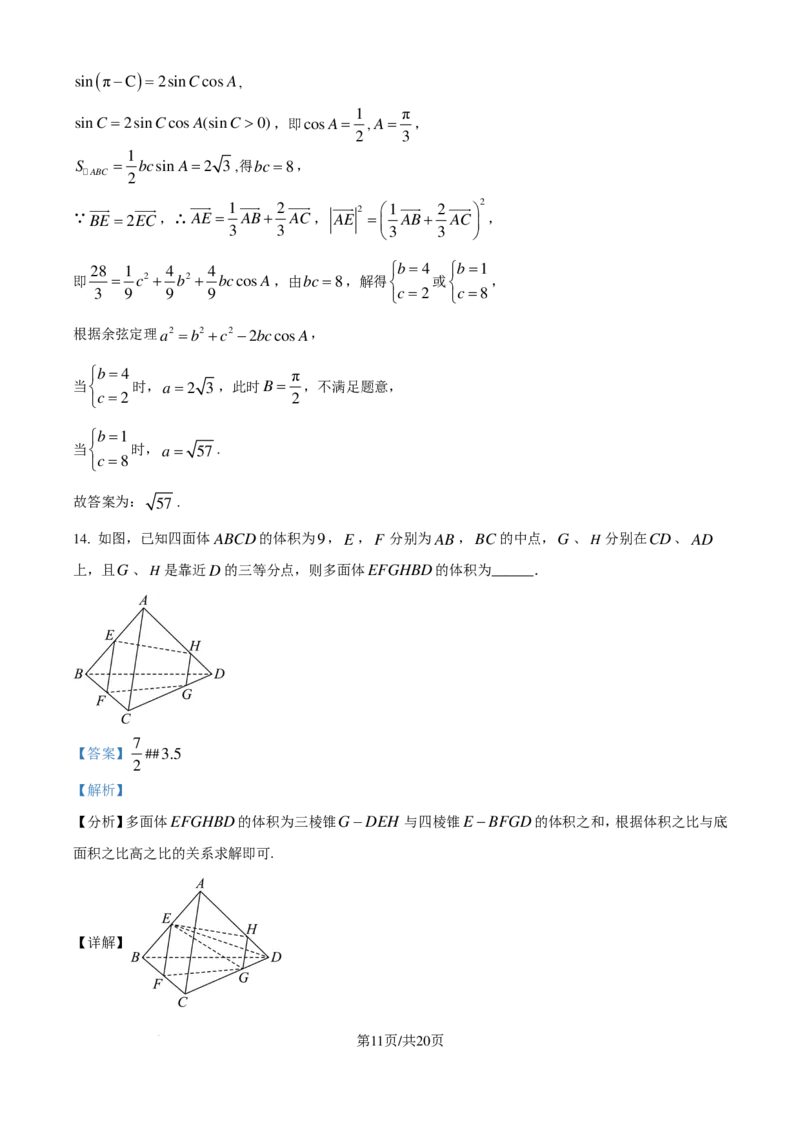
对C:当 时,如图:
|𝐴𝐴𝐴𝐴|=4
第8页/共20页
学科网(北京)股份有限公司2 3 2 2 6 4 1
sin∠ACP= = ,cos∠ACP= = ,所以cos∠ACB= −1= >0,
2 3 3 2 3 3 3 3
所以∠ACB为锐角,又随着直线AB斜率的变化,∠ACB最大可以为平角,
所以存在直线l使得CA⊥CB.故C正确;
对D:如图:
直线CP与圆C交于M 、N 两点,链接AM ,BN ,
因为∠MAP=∠BNP,∠APM =∠NPB,所以APM NPB.
AP MP ( )( )
所以 = ⇒ AP ⋅ BP = MP ⋅ NP = 2 3−2 2 2 3+2 2 =4.
NP BP
1
又S = PA ⋅ PC ⋅sin∠APC = 2 PA ⋅sin∠APC,S = 2 PB ⋅sin∠BPC,
PAC
2
PBC
且sin∠APC =sin∠BPC.
所以S ⋅S =2 PA ⋅ PB ⋅sin2∠APC =8sin2∠APC ≤8,
PAC PBC
当且仅当sin∠APC =1,即AB⊥CP时取“=”.故D正确.
故选:ACD
【点睛】方法点睛:在求S ⋅S 的最大值时,应该先结合三角形相似(或者蝴蝶定理)求出
△PAC △PBC
AP ⋅ BP 为定值,再结合三角形的面积公式求S ⋅S 的最大值.
△PAC △PBC
三、填空题:本题共 3小题,每小题 5分,共 15分.
第9页/共20页
学科网(北京)股份有限公司12. 实数x、 y满足x2 + y2 =4,则( x−4 )2 +( y+3 )2的最大值是______.
【答案】49
【解析】
【分析】根据( x−4 )2 +( y+3 )2几何意义为圆上的点 ( x,y ) 与 ( 4,−3 ) 距离的平方,找出圆上的与 ( 4,−3 ) 的
最大值,再平方即可求解.
【详解】解:由题意知:设 p ( x,y ) ,A ( 4,−3 ) ,
( )
则 p x,y 为圆x2 + y2 =4上的点,
圆x2 + y2 =4的圆心 ,半径r =2,
𝑂𝑂(0,0)
则( x−4 )2 +( y+3 )2表示圆上的点 p ( x,y ) 与A ( 4,−3 ) 距离的平方,
又因为 PA = AO +r = ( 4−0 )2 +(−3−0 )2 +2=7,
max
所以 PA 2 =72 =49;
max
故( x−4 )2 +( y+3 )2的最大值是49.
故答案为:49.
13. 记ABC的三个内角A,B,C的对边分别为a,b,c,已知acosB=( 2c−b ) cosA,其中
π 2 21
B ≠ ,若ABC的面积S =2 3,BE =2EC,且 AE = ,则BC的长为______.
2 3
【答案】 57
【解析】
π
【分析】利用正弦定理对acosB=( 2c−b ) cosA化简,可得A= ,再由三角形面积公式求出bc=8,
3
1 2
根据题意写出AE = AB+ AC,等式两边平方后,可求出b,c的值,由余弦定理
3 3
a2 =b2 +c2 −2bccosA,求出BC的长.
【详解】acosB=( 2c−b ) cosA,
由正弦定理可得:sinAcosB=2sinCcosA−sinBcosA,
sinAcosB+cosAsinB=2sinCcosA,
sin ( A+B )=2sinCcosA,
第10页/共20页
学科网(北京)股份有限公司sin ( π−C )=2sinCcosA,
1 π
sinC =2sinCcosA(sinC >0),即cosA= ,A= ,
2 3
1
S = bcsinA=2 3,得bc=8,
ABC
2
1 2 2 1 2 2
∵BE =2EC,∴AE = AB+ AC, AE = AB+ AC ,
3 3 3 3
28 1 4 4 b=4 b=1
即 = c2 + b2 + bccosA,由bc=8,解得 或 ,
3 9 9 9 c=2 c=8
根据余弦定理a2 =b2 +c2 −2bccosA,
b=4 π
当 时,a=2 3,此时B= ,不满足题意,
c=2 2
b=1
当 时,a= 57.
c=8
故答案为: 57 .
14. 如图,已知四面体ABCD的体积为9,E,F 分别为AB,BC的中点,G、H 分别在CD、AD
上,且G、H 是靠近D的三等分点,则多面体EFGHBD的体积为______.
7
【答案】 ##3.5
2
【解析】
【分析】多面体EFGHBD的体积为三棱锥G−DEH 与四棱锥E−BFGD的体积之和,根据体积之比与底
面积之比高之比的关系求解即可.
【详解】
第11页/共20页
学科网(北京)股份有限公司连接ED,EG,
1
因为H 为 上的靠近D的三分点,所以DH = AD,
3
因为E为𝐴𝐴𝐴𝐴的中点,所以点E到 的距离为点B到 的距离的一半,
1
所以S 𝐴𝐴𝐴𝐴= S , 𝐴𝐴𝐴𝐴 𝐴𝐴𝐴𝐴
DEH
6
BAD
又G为 上靠近D的三分点,
所以点G 𝐶𝐶𝐴𝐴到平面ABD的距离为点C到平面ABD的距离的 ,
1
1 1 1 1 1 3
所以V = V = × V = ×9= ,
G−DEH
6
G−BAD
6 3
C−BAD
18 2
1 2
S =S −S =S − S = S ,
四边形BFGD BCD FCG BCD
3
BCD
3
BCD
2 2 1 1
所以V = V = × V = ×9=3,
E−BFGD
3
E−BCD
3 2
A−BCD
3
1 7
所以多面体EFGHBD的体积为V +V = +3= .
G−DEH E−BFGD
2 2
7
故答案为: .
2
【点睛】关键点点睛:将多面体转化为两个锥体的体积之和,通过体积之比与底面积之比高之比的关系求
解.
四、解答题:本题共 5小题,共 77分.解答应写出文字说明、证明过程或演算步骤.
15. 在对某高中1500名高二年级学生的百米成绩的调查中,采用按学生性别比例分配的分层随机抽样抽取
100人,已知这1500名高二年级学生中男生有900人,且抽取的样本中男生成绩的平均数和方差分别为
13.2秒和13.36,女生成绩的平均数和方差分别为15.2秒和17.56.
(1)求抽取的总样本的平均数;
(2)试估计高二年级全体学生的百米成绩的方差.
【答案】(1)14 (2)16
【解析】
【分析】(1)先确定样本中男生、女生的人数,再求总样本的平均数.
(2)根据方差的概念,计算总样本的方差.
【小问1详解】
100
样本中男生的人数为:900× =60;女生的人数为:100−60=40.
1500
60×13.2+40×15.2
所以总样本的平均数为:x= =14.
100
【小问2详解】
第12页/共20页
学科网(北京)股份有限公司记总样本的方差为s2,
1 { }
则s2 = 60× 13.36+( 13.2−14 )2+40× 17.56+( 15.2−14 )2 =16.
100
所以,估计高二年级全体学生的百米成绩的方差为16.
16. 在平面直角坐标系xOy中,ABC的顶点A的坐标为
(−4,2 )
,∠ACB的角平分线所在的直线方程
为x− y+1=0,AC边上中线BM 所在的直线方程为2x+ y−2=0.
(1)求点C的坐标;
(2)求直线BC的方程.
【答案】(1)C(3,4);
(2)7x−2y−13=0.
【解析】
m−4 m+3
【分析】(1)设C(m,m+1),则M( , ),代入2x+ y−2=0,求解即可;
2 2
(2)设直线BC的方程为:x+ny−3−4n=0,在直线x− y+1=0取点P(0,1),利用点P到直线AC的
距离等于点P到直线BC的距离,求解即可.
【小问1详解】
解:由题意可知点C在直线x− y+1=0上,
所以设C(m,m+1),
m−4 m+3
所以AC中点M( , ),
2 2
m−4 m+3
又因为点M( , )在直线2x+ y−2=0上,
2 2
m+3
所以m−4+ −2=0,解得m=3,
2
所以C(3,4);
【小问2详解】
解:因为C(3,4),
设直线BC的方程为:x+ny−3−4n=0,
又因为A(−4,2),
所以直线AC的方程为:2x−7y+22=0,
第13页/共20页
学科网(北京)股份有限公司又因为∠ACB的角平分线所在的直线方程为x− y+1=0,
在直线x− y+1=0取点P(0,1),
则点P到直线AC的距离等于点P到直线BC的距离,
15 |3+3n|
即有 = ,整理得14n2 +53n+14=0,
53 1+n2
7 2
解得:n=− 或n=− ,
2 7
7
当n=− 时,所求方程即为直线AC的方程,
2
2
所以n=− ,
7
所以直线BC的方程为: 7x−2y−13=0.
17. 直三棱柱ABC−ABC 中,AB= AC = AA =2,其中E,F,D分别为棱BC,BB,AC 的中点,已
1 1 1 1 1 1 1
知AF ⊥ AC ,
1 1
(1)求证:AF ⊥DE;
(2)设平面EFD与平面ABC的交线为直线m,求直线AC与直线m所成角的余弦值.
【答案】(1)证明见解析
2 13
(2)
13
第14页/共20页
学科网(北京)股份有限公司【解析】
【分析】(1)取AB的中点G,连接EG,AG证得四边形ADEG为平行四边形,得到DE//AG,利用
1 1
AAG≌ABF ,证得∠AHG =90,得到AF ⊥ AG,即可证得AF ⊥DE;
1 1
(2)根据题意,证得AC ⊥平面ABB A ,得到AC ⊥ AB ,以A为原点,建立空间直角坐标系,求得
1 1 1 1 1 1 1 1
AC =(0,2,0),再取AC的中点M ,延长MB,DF交于点N ,得到直线AC与直线m所成角,即为直线
AC与直线EN 所成角,求得N(4,−1,0),得到EN =(3,−2,0),结合向量的夹角公式,即可求解.
【小问1详解】
证明:取AB的中点G,连接EG,AG,
1
1
因为E的中点,可得EG//AC,且EG = AC,
2
1
又因为AD//AC,且AD= AC,所以EG//AD,且EG = AD,
1 1 2 1 1
所以四边形ADEG 为平行四边形,所以DE//AG,
1
在正方形ABB A 中,可得AAG≌ABF ,所以∠AGA=∠AFB,
1 1 1 1
因为∠AFB+∠AFB=90,所以∠AFB+∠AGA=90,
1
在AGH 中,可得∠AHG =90,所以AF ⊥ AG,
1
又因为DE//AG,所以AF ⊥DE.
1
【小问2详解】
解:在直三棱柱ABC−ABC 中,可得AA ⊥平面ABC ,
1 1 1 1 1 1 1
因为AC ⊂平面ABC ,所以AA ⊥ AC ,
1 1 1 1 1 1 1 1
又因为AF ⊥ AC ,且AA ∩ AF = A,AA,AF ⊂平面ABB A ,所以AC ⊥平面ABB A ,
1 1 1 1 1 1 1 1 1 1
因为AB ⊂平面ABB A ,所以AC ⊥ AB ,
1 1 1 1 1 1 1 1
即直三棱柱ABC−ABC 的底面为等腰直角三角形,
1 1 1
以A为原点,以AB,AC,AA所在的直线分别为x,y,z轴,建立空间直角坐标系,
1
如图所示,因为AB= AC = AA =2,可得A(0,0,0),C(0,2,0),则AC =(0,2,0),
1
第15页/共20页
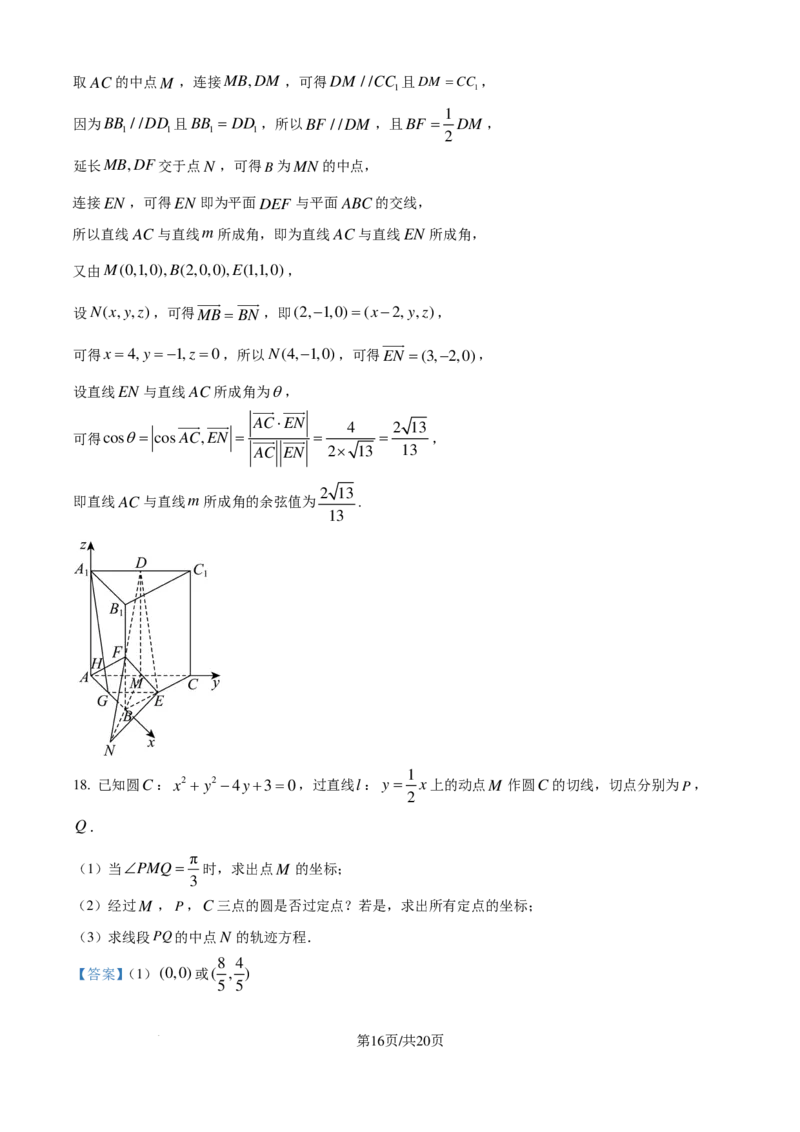
学科网(北京)股份有限公司取AC的中点M ,连接MB,DM ,可得DM //CC 且DM =CC ,
1 1
1
因为BB //DD 且BB = DD ,所以BF //DM ,且BF = DM ,
1 1 1 1
2
延长MB,DF交于点N ,可得B为MN的中点,
连接EN ,可得EN 即为平面DEF 与平面ABC的交线,
所以直线AC与直线m所成角,即为直线AC与直线EN 所成角,
又由M(0,1,0),B(2,0,0),E(1,1,0),
设N(x,y,z),可得MB= BN ,即(2,−1,0)=(x−2,y,z),
可得x=4,y =−1,z =0,所以N(4,−1,0),可得EN =(3,−2,0),
设直线EN 与直线AC所成角为θ,
AC⋅EN
4 2 13
可得cosθ= cosAC,EN = = = ,
AC EN 2× 13 13
2 13
即直线AC与直线m所成角的余弦值为 .
13
1
18. 已知圆C:x2 + y2 −4y+3=0,过直线l: y = x上的动点M 作圆C的切线,切点分别为P,
2
Q.
π
(1)当∠PMQ= 时,求出点M 的坐标;
3
(2)经过M ,P,C三点的圆是否过定点?若是,求出所有定点的坐标;
(3)求线段PQ的中点N 的轨迹方程.
8 4
【答案】(1)(0,0)或( , )
5 5
第16页/共20页
学科网(北京)股份有限公司4 2
(2)过定点(0,2)或( , )
5 5
1 7
(3)x2 + y2 − x− y+3=0
4 2
【解析】
【分析】(1)点M 在直线l上,设M(2m,m),由对称性可知∠CMP=30,可得MC =2,从而可得点
M 坐标.
m
(2)MC 的中点Qm, +1,因为MP是圆P的切线,进而可知经过C,P,M三点的圆是以Q为圆
2
心,以MC为半径的圆,进而得到该圆的方程,根据其方程是关于m的恒等式,进而可求得x和y,得到
结果;
1 3
(3)结合(2)将两圆方程相减可得直线PQ的方程,且得直线PQ过定点R , ,由几何性质得
4 2
MN ⊥ RN ,即点N在以MR为直径的圆上,进而可得结果.
【小问1详解】
(1)
直线l的方程为x−2y =0,点M 在直线l上,设M(2m,m),
π
因为∠PMQ= ,由对称性可得:由对称性可知∠CMP=30,
3
由题CP =1所以MC =2,所以(2m)2 +(m−2)2 =4,
4 8 4
解之得:m =0,m = 故所求点M 的坐标为(0,0)或( , ).
5 5 5
【小问2详解】
m
设M(2m,m),则MC 的中点E(m, +1),因为MP是圆C的切线,
2
所以经过C,P,M 三点的圆是以Q为圆心,以ME为半径的圆,
m m
故圆E方程为:(x−m)2 +(y− −1)2 =m2 +( −1)2
2 2
第17页/共20页
学科网(北京)股份有限公司化简得:x2 + y2 −2y−m(2x+ y−2)=0,此式是关于m的恒等式,
4
x=
x2 + y2 −2y =0, x=0 5
故{ 解得 或 ,
2x+ y−2=0, y =2
2
y =
5
4 2
所以经过C,P,M 三点的圆必过定点(0,2)或( , ).
5 5
【小问3详解】
x2 + y2 −2mx−( m+2 ) y+2m=0,
由
x2 + y2 −4y+3=0
可得PQ:2mx+( m−2 ) y+3−2m=0,即m ( 2x+ y−2 )−2y+3=0,
2x+ y−2=0, 1 3
由 可得PQ过定点R , .
2y−3=0 4 2
因为N为圆E的弦PQ的中点,所以MN ⊥ PQ,即MN ⊥ RN ,
故点N在以MR为直径的圆上,
1 7
点N的轨迹方程为x2 + y2 − x− y+3=0.
4 2
19. 四棱锥P−ABCD中,底面ABCD为等腰梯形,AB =2BC =2CD =4,侧面PAD为正三角形;
(1)当BD⊥ PD时,线段PB上是否存在一点Q,使得直线AQ与平面ABCD所成角的正弦值为
2 PQ
?若存在,求出 的值;若不存在,请说明理由.
4 QB
(2)当PD与平面BCD所成角最大时,求三棱锥P−BCD的外接球的体积.
【答案】(1)存在;1.
52 39
(2) π
27
第18页/共20页
学科网(北京)股份有限公司【解析】
【分析】(1)先证平面PAD⊥平面ABCD,可得线面垂直,根据垂直,可建立空间直角坐标系,用空间向
量,结合线面角的求法确定点Q的位置.
(2)根据PD与平面BCD所成角最大,确定平面PAD⊥平面ABCD,利用(1)中的图形,设三棱锥
P−BCD的外接球的球心,利用空间两点的距离公式求球心和半径即可.
【小问1详解】
因为底面ABCD为等腰梯形,AB =2BC =2CD =4,
所以∠BAD=60°,∠BCD=120°,∠CBD=∠ABD=30°,所以∠ADB=90°.
所以BD⊥ AD,
又BD⊥ PD,AD,PD⊂平面PAD,且ADPD= D,所以BD⊥平面PAD.
又BD⊂平面ABCD,所以平面PAD⊥平面ABCD.
取AD中点O,因为△PAD是等边三角形,所以PO⊥ AD,
平面PAD∩平面ABCD= AD,
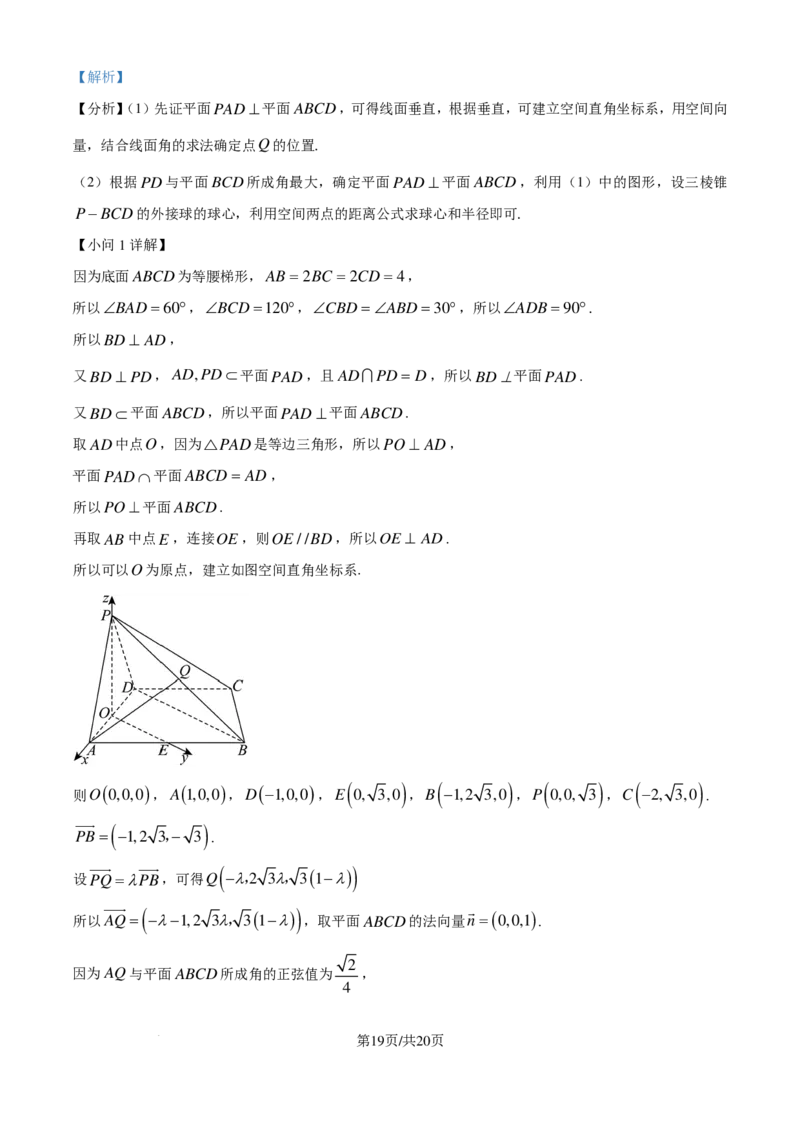
所以PO⊥平面ABCD.
再取AB中点E,连接OE,则OE//BD,所以OE ⊥ AD.
所以可以O为原点,建立如图空间直角坐标系.
( ) ( ) ( ) ( )
则O ( 0,0,0 ) ,A ( 1,0,0 ) ,D (−1,0,0 ) ,E 0, 3,0 ,B −1,2 3,0 ,P 0,0, 3 ,C −2, 3,0 .
( )
PB= −1,2 3,− 3 .
( )
设PQ=λPB,可得Q −λ,2 3λ,3 ( 1−λ)
( )
所以AQ= −λ−1,2 3λ,3 ( 1−λ) ,取平面ABCD的法向量n =( 0,0,1 ) .
2
因为AQ与平面ABCD所成角的正弦值为 ,
4
第19页/共20页
学科网(北京)股份有限公司
AQ⋅n
3
( 1−λ)
2 1
所以 = = ,解得λ= 或λ=5(舍去).
AQ ⋅ n (λ+1 )2 +12λ2 +3 ( 1−λ)2 4 2
2 PQ
所以:线段PB上存在一点Q,使得直线AQ与平面ABCD所成角的正弦值为 ,此时 =1.
4 QB
【小问2详解】
当平面PAD⊥平面ABCD时, PD与平面BCD所成角为∠PDA.
当平面PAD与平面ABCD不垂直时,过P做PH ⊥平面ABCD,连接HD,
则∠PDH 为PD与平面BCD所成角,因为PH < PO,
PH PO
sin∠PDH = ,sin∠PDA= ,sin∠PDH