文档内容
学科网(北京)股份有限公司
西北狼教育联盟2024 年秋季开学学业调研数学高二评分细则
题号
1
2
3
4
5
6
7
8
答案
B
A
A
B
D
C
B
C
题号
9
10
11
12
13
14
答案
AC
BC
ACD
10
4 6
8,24
−
7.【解析】 依题意得
45
MAB
=
,
180
75
105
MBA =
−
=
,
在 中,
600 15
9000
AB =
=
米,
180
45
105
30
AMB =
−
−
=
,
由正弦定理得sin 45
sin30
BM
AB
=
,得
2
9000
2
9000 2
1
2
BM
=
=
米,
又
sin 75
9000 2 sin(45
30 )
BM
=
+
9000 2(sin 45 cos30
cos45 sin30 )
=
+
2
3
2
1
9000 2(
)
2
2
2
2
=
+
3
1
9000(
)
2
2
=
+
4500( 3
1)
=
+
所以该山顶的海拔高度为16000
sin 75
BM
−
16000
4500( 3
1)
=
−
+
11500
4500 3
=
−
11500
4500 1.732
−
= 3706米.故选:B
8.【详解】因为𝐵𝐷
⃗⃗⃗⃗⃗⃗ =
2
3 𝐵𝐶
⃗⃗⃗⃗⃗ ,所以𝐶𝐷
⃗⃗⃗⃗⃗ =
1
3 𝐶𝐵
⃗⃗⃗⃗⃗ ,因为𝐶𝐸
⃗⃗⃗⃗⃗ = 𝑥𝐶𝐴
⃗⃗⃗⃗⃗ + 𝑦𝐶𝐵
⃗⃗⃗⃗⃗ ,所以𝐶𝐸
⃗⃗⃗⃗⃗ = 𝑥𝐶𝐴
⃗⃗⃗⃗⃗ +
3𝑦𝐶𝐷
⃗⃗⃗⃗⃗ ,
因为𝐴, 𝐷, 𝐸三点共线,所以𝑥+ 3𝑦= 1,𝑥> 0, 𝑦> 0,
所以
2
𝑥+
6
𝑦= (
2
𝑥+
6
𝑦) ⋅(𝑥+ 3𝑦) = 20 +
6𝑦
𝑥+
6𝑥
𝑦≥20 + 2√
6𝑦
𝑥×
6𝑥
𝑦= 20 + 12 = 32,
当且仅当
6𝑦
𝑥=
6𝑥
𝑦,即𝑥= 𝑦=
1
4时取等号,所以
2
𝑥+
6
𝑦的最小值是32.
故选:C
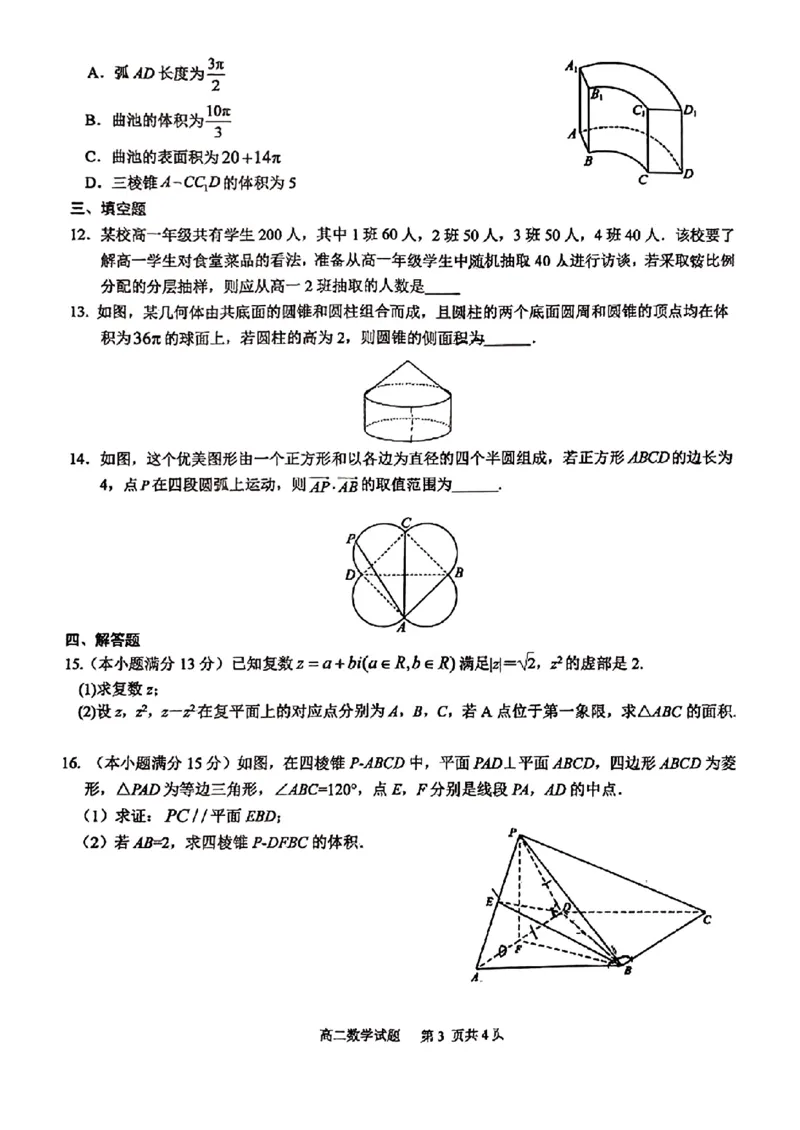
11.【解析】设弧AD 所在圆的半径为R ,弧BC 所在圆的半径为r ,
因为弧AD 的长度是弧BC 长度的3 倍,底面扇环所对的圆心角为π
2 ,
所以π
π
3
2
2
R
r
=
,解得
3
R
r
=
,所以
2
2
CD
R
r
r
=
−
=
=
,可得
3,
1
R
r
=
= ,
所以弧的AD 的长度为3π
2 ,所以A 正确;
AMB
学科网(北京)股份有限公司
该曲池的体积为
2
2
1
1
1
9
1
(
π
π
)
(
π
π) 5
10π
4
4
4
4
V
R
r
AA
=
−
=
−
=
,所以B 不正确;
曲池的表面积为
2
2
1
1
1
1
1
(
2π
2π )
2
2
π(
)
4
4
4
S
R
r
AA
CD
AA
R
r
=
+
+
+
−
2
2
1
1
π (3 1) 5
2 2 5
π(3
1 )
20 14π
2
2
=
+
+ +
−
=
+
,所以C 正确;
三棱锥
1
A
CC D
−
的体积为
1
1
1
1
1
2 5 3
5
2
3
2
A CC D
CD D
V
S
R
−
=
=
= ,所以D 正确.
故选:ACD.
13.【详解】其中,O 是球心,E 是圆锥的顶点,EC 是圆锥的母线,
由题意可知
3
4 π
36π
3 R =
,解得
3
R =
,
由于圆柱的高为2,
1
OD = ,
3 1
2
DE =
−=
,
2
2
3
1
2 2
DC =
−
=
,
母线
2
2
8
2 3
EC =
+
=
,
∴圆锥的侧面积为
π
2 2
2 3π
4 6π
S
DC EC
=
=
=
.
故答案为:4 6π
14.【解析】如图,以点A 为原点,分别以
,
AB AD 所在直线为,x y 轴建立坐标系.
因
|
| |
| cos
,
4 |
| cos
,
AP AB
AP
AB
AP AB
AP
AP AB
=
=
,
而|
| cos
,
AP
AP AB
表示AP 在AB 方向上的投影向量的数量,
由图不难发现,设过正方形的中心作与x 轴平行的直线与左右两个半圆分别交于点
1
2
,
P P ,
则当点P 与点
1P 重合时,投影向量的数量最大,当点P 与点
2P 重合时,投影向量的数量最
小.
易得
1
2
(6,2),
( 2,2)
P
P −
,则|
| cos
,
AP
AP AB
的最大值为6,最小值为2
−,
故8
24
AP AB
−
.
四、解答题
15.(本小题满分13 分)
解 (1)z=a+bi(a,b∈R),
学科网(北京)股份有限公司
则z2=a2-b2+2abi,…………………………………………………….…….2 分
由题意得a2+b2=2 …………………………………………………….…….4 分
且2ab=2, ……………………………………………………..…….5 分
解得a=b=1 或a=b=-1,………………………………………………….6 分
所以z=1+i 或z=-1-i. ………………………………………………….….7 分
(2)因为A 位于第一象限,所以z=1+i,…………………………..….…….8 分
z2=2i, ……………………………………………………….9 分
z-z2=1-i,………………………………………………..…………….…….10 分
所以A(1,1),B(0,2),C(1,-1), …………………………………..….12 分
所以S△ABC=1. ……………………………………….13 分
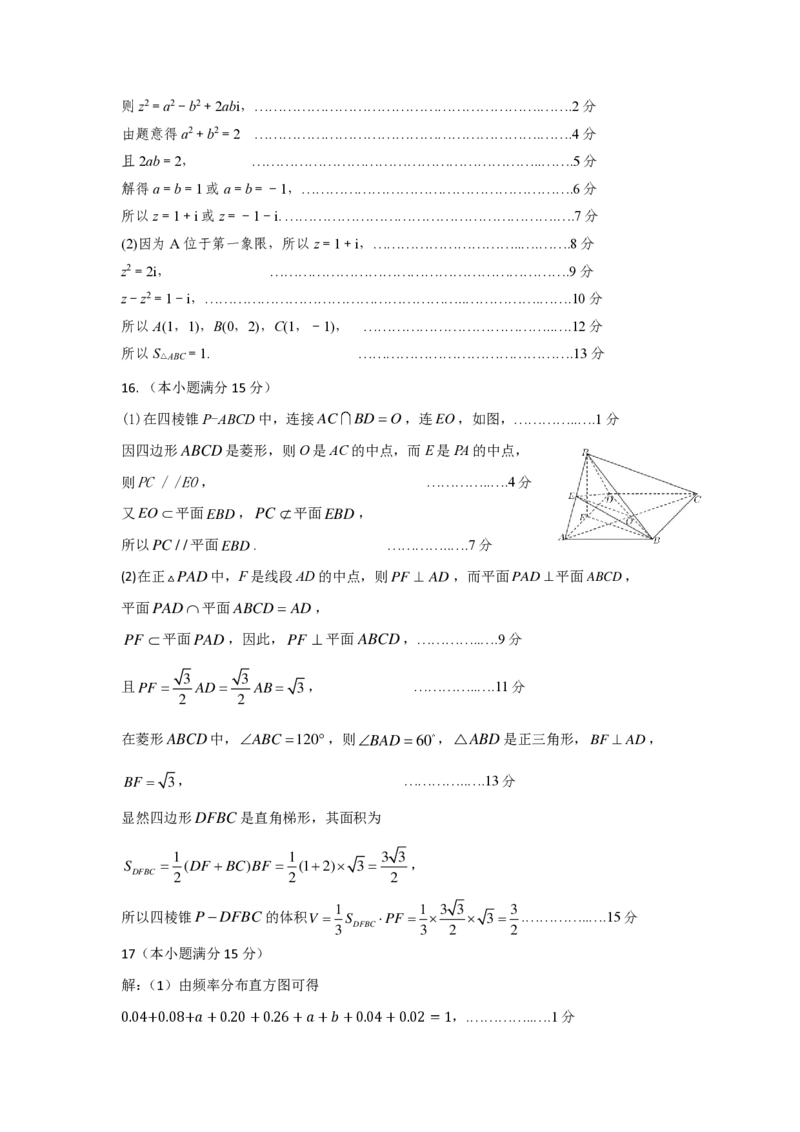
16. (本小题满分15 分)
(1)在四棱锥P-ABCD 中,连接AC
BD
O
=
,连EO ,如图,…………..….1 分
因四边形ABCD 是菱形,则O 是AC 的中点,而E 是PA 的中点,
则
/ /
PC
EO , …………..….4 分
又EO 平面EBD ,PC 平面EBD ,
所以
/ /
PC
平面EBD . …………..….7 分
(2)在正PAD 中,F 是线段AD 的中点,则PF
AD
⊥
,而平面PAD ⊥平面ABCD ,
平面PAD 平面ABCD
AD
=
,
PF 平面PAD ,因此,PF ⊥平面ABCD ,…………..….9 分
且
3
3
3
2
2
PF
AD
AB
=
=
=
, …………..….11 分
在菱形ABCD 中,
120
ABC
=
,则
60
BAD
=
,
ABD
△
是正三角形,BF
AD
⊥
,
3
BF =
, …………..….13 分
显然四边形DFBC 是直角梯形,其面积为
1
1
3 3
(
)
(1
2)
3
2
2
2
DFBC
S
DF
BC BF
=
+
=
+
=
,
所以四棱锥P
DFBC
−
的体积
1
1
3 3
3
3
3
3
2
2
DFBC
V
S
PF
=
=
=
.…………..….15 分
17(本小题满分15 分)
解:(1)由频率分布直方图可得
0.04+0.08+𝑎+ 0.20 + 0.26 + 𝑎+ 𝑏+ 0.04 + 0.02 = 1,.…………..….1 分
学科网(北京)股份有限公司
又0.4𝑎= 𝑏,则𝑎= 0.15,𝑏= 0.06, .…………..…...3 分
该市居民用水的平均数估计为:
𝑥= 0.5 × 0.04 + 1.5 × 0.08 + 2.5 × 0.15 + 3.5 × 0.20 + 4.5 × 0.26
+5.5 × 0.15 + 6.5 × 0.06 + 7.5 × 0.04 + 8.5 × 0.02 = 4.07;.…………..6 分
(2)由频率分布直方图可得,
月均用水量不超过2 吨的频率为:0.04 + 0.08 = 0.12,
则月均用水量不低于2 吨的频率为:1 −0.12 = 0.88,.…………..….8 分
所以全市40 万居民中月均用水量不低于2 吨的人数为:
40 × 0.88 = 35.2(万); .…………..….10 分
(3)由频率分布直方图知月均用水量不超过6 吨的频率为:0.88,
月均用水量不超过5 吨的频率为0.73,
则85%的居民每月的用水量不超过的标准𝑥(吨),5 < 𝑥< 6,.…………..….12 分
∴0.73 + 0.15(𝑥−5) = 0.85 ,解得𝑥= 5.8,
即标准为5.8 吨. .……………….….15 分
18(本小题满分17 分)
(1)因为sin𝐴−sin𝐶=
𝑏
𝑎+𝑐(sin𝐵−sin𝐶),
所以𝑎−𝑐=
𝑏
𝑎+𝑐(𝑏−𝑐), .……………….….2 分
得𝑏2 + 𝑐2 −𝑎2 = 𝑏𝑐, .……………….….3 分
所以cos𝐴=
𝑏2+𝑐2−𝑎2
2𝑏𝑐
=
1
2, .……………….….5 分
因为𝐴∈(0, 𝜋),所以𝐴=
𝜋
3. .……………….….7 分
(2)分三种情况求解:
选择①𝑎= 3,因为𝐴=
𝜋
3 , 𝑎= 3,
由正弦定理得
𝑏
sin𝐵=
𝑐
sin𝐶=
𝑎
sin𝐴= 2√3, .……………….….9 分
即△𝐴𝐵𝐶的周长𝑙= 𝑎+ 𝑏+ 𝑐= 2√3sin𝐵+ 2√3sin𝐶+ 3 .……………….….10 分
𝑙= 2√3sin𝐵+ 2√3sin (
2𝜋
3 −𝐵) + 3 .……………...….11 分
= 3√3sin𝐵+ 3cos𝐵+ 3 .……………….….13 分
= 6sin (𝐵+
𝜋
6) + 3, .………………..….14 分
学科网(北京)股份有限公司
因为𝐵∈(0,
2𝜋
3 ),所以
𝜋
6 < 𝐵+
𝜋
6 <
5𝜋
6 ,
1
2 < sin(𝐵+
𝜋
6) ⩽1,.……………….….16 分
即△𝐴𝐵𝐶周长的取值范围是(6,9]. .……………….….17 分
选择②𝑏= 3,因为𝐴=
𝜋
3 , 𝑏= 3,
由正弦定理得𝑎=
3√3
2sin𝐵, .……………...….….8 分
𝑐=
3sin𝐶
sin𝐵=
3sin(2𝜋
3 −𝐵)
sin𝐵
=
3√3cos𝐵
2sin𝐵+
3
2 .………………….….11 分
即△𝐴𝐵𝐶的周长𝑙= 𝑎+ 𝑏+ 𝑐=
3√3
2sin𝐵+
3√3cos𝐵
2sin𝐵+
9
2 .………………….….12 分
= 3√3(1 + cos𝐵)
2sin𝐵
+ 9
2 =
6√3cos2 𝐵
2
4sin 𝐵
2 cos 𝐵
2
+ 9
2
=
3√3
2tan𝐵
2
+
9
2, .………………….….15 分
因为𝐵∈(0,
2𝜋
3 ),所以0 <
𝐵
2 <
𝜋
3,所以0 < tan
𝐵
2 < √3,.………………….….16 分
即△𝐴𝐵𝐶周长的取值范围是(6, +∞). .………………….….17 分
选择③𝑆△𝐴𝐵𝐶= 3√3.
因为𝐴=
𝜋
3 , 𝑆△𝐴𝐵𝐶=
1
2 𝑏𝑐sin𝐴= √3
4 𝑏𝑐= 3√3, .………………….….8 分
得𝑏𝑐= 12, .………………….….9 分
由余弦定理得𝑎2 = 𝑏2 + 𝑐2 −𝑏𝑐= (𝑏+ 𝑐)2 −3𝑏𝑐= (𝑏+ 𝑐)2 −36,.…………….12 分
即△𝐴𝐵𝐶的周长𝑙= 𝑎+ 𝑏+ 𝑐= √(𝑏+ 𝑐)2 −36 + 𝑏+ 𝑐, .………………….13 分
因为𝑏+ 𝑐⩾2√𝑏𝑐= 4√3,当且仅当𝑏= 𝑐= 2√3时等号成立,.……………….….15 分
所以𝑙⩾√(4√3)2 −36 + 4√3 = 6√3. .…………………….16 分
即△𝐴𝐵𝐶周长的取值范围是[6√3, +∞). .…………………….….17 分
19.(本小题满分17 分)
【解】(1)在直三棱柱
1
1
1
ABC
A B C
−
中,
1
AA ⊥平面ABC,
,
AC AB 平面ABC,
则
1
AA
AC
⊥
,
1
AA
AB
⊥
,所以点A 的曲率为
π
2π
π
2
2
3
2
BAC
−
−
=
,.…………1 分
所以
π
3
BAC
=
.因为AB
AC
=
,所以△ABC 为正三角形. .………………….….2 分
因为N 为AB 的中点,所以CN
AB
⊥
. .………………….….3 分
又
1
AA ⊥平面ABC,CN 平面ABC,所以
1
AA
CN
⊥
, .………………….….4 分
学科网(北京)股份有限公司
因为
1
AA
AB
A
=
,
1
AA
AB
、
平面
1
1
ABB A ,所以CN ⊥平面
1
1
ABB A ..……….….5 分
(2)取
1
AB 的中点D,连接DM,DN.
因为N 为AB 的中点,所以
1
/ /
DN
BB 且
1
1
2
DN
BB
=
..………………….….6 分
又
1
/ /
CM
BB 且
1
1
2
CM
BB
=
,所以
/ /
DN
CM 且DN
CM
=
,.…………..….7 分
所以四边形CNDM 为平行四边形,则
/ /
DM
CN . .…………….….8 分
由(1)知CN ⊥平面
1
1
ABB A ,则DM ⊥平面
1
1
ABB A . .…………….….9 分
又DM 平面
1
AMB ,所以平面
1
AMB ⊥平面
1
1
ABB A . .…………….…10 分
(3)取BC 的中点F,连接AF,则AF
BC
⊥
. .…………….…11 分
因为
1
BB ⊥平面ABC,AF 平面ABC,所以
1
BB
AF
⊥
,
因为
1
BB
BC
B
=
,
1
BB
BC
、
平面
1
1
BB C C ,所以AF ⊥平面
1
1
BB C C .…….…12 分
又
1
B M 平面
1
1
BB C C ,所以
1
AF
B M
⊥
,过F 作
1
B M 的垂线,垂足为H,连接AH,
则
1B M
FH
⊥
,又
,
AF
FH
F AF
FH
=
、
平面AFH ,所以
1
B M ⊥平面AFH ,.…13 分
又AH 平面AFH ,
1
AH
B M
⊥
,
所以∠AHF 为二面角
1
1
A
MB
C
−
−
的平面角的补角. .…………….…14 分
设
1
B M
BC
E
=
,
2
AB =
,则
3
AF =
,
1
2
3
EF = +
=
,
2 2
ME =
.
由等面积法可得1
1
2
2
ME FH
EF CM
=
,则
3 2
3
2 2
2
EF CM
FH
ME
=
=
=
,
则
6
tan
3
AF
AHF
FH
=
=
, .…………….…16 分
故二面角
1
1
A
MB
C
−
−
的正切值为
6
3
−
. .…………….…17 分