文档内容
2024——2025 学年高二下学期期中考试
非篮球迷 45 10
数学试卷
附: ,
P(χ2≥k) 0.10 0.05 0.01
考试范围:选择性必修一、二、三 命题人:王一森 时间:120 分钟 满分:150 分
一、单选题:本题共 8 小题,每小题 5 分,共 40 分。每题所给出的 4 个选项中有且只有一个是符合题 k 2.706 3.841 6.635
意的。
A.有 90%的把握认为是否是篮球迷与性别有关
1.已知数列{a }满足 ,则 是它的( ) B.有 99%的把握认为是否是篮球迷与性别有关
n
C.在犯错误的概率不超过 0.05 的前提下,可以认为是否是篮球迷与性别有关
A.第 6 项 B.第 7 项 C.第 8 项 D.第 9 项
D.在犯错误的概率不超过 0.01 的前提下,可以认为是否是篮球迷与性别有关
2.设 A,B 为两个事件,若 , ,则 P(A|B)等于( )
8.设等差数列{a }的前 n 项和为 S ,公差为 d,若 a +a >0,a <0,则下列结论不正确的是( )
n n 8 9 9
A. B. C. D.
A.d<0
3.已知函数 f(x)=ex+2x,则曲线 y=f(x)在点(0,f(0))处的切线方程为( )
B.当 n=8 时,S 取得最大值
n
A.y=2x+1 B.y=3x+1 C.y=2x D.y=3x
C.a +a +a >0
2 5 12
4.已知随机变量 ,若 E(X)=2,则 P(X=2)=( ) D.使得 S >0 成立的最大自然数 n 是 15
n
二、多选题:本题共 3 小题,每小题 6 分,共 18 分。每题所给出的 4 个选项中都有不止一个选项是
符 A. B. C. D.
合题意的,都选对得全分,部分选对得部分分,有错选不得分。
5.已知数列{a }为等比数列,其中 a ,a 为方程 x2+2025x+3=0 的两根,则 a =( ) 9.下列有关线性回归分析的问题中,正确的是( )
n 6 10 8
A. B. C. D.
A.线性回归方程 至少经过点(x ,y ),(x ,y ),(x ,y ),…,(x ,y )中的一个点
1 1 2 2 3 3 n n
6.某校高三年级甲、乙两名学生平时测试的数学成绩 X ~N( , ),X ~N( , ),其中
1 1 2 2 1
B.两个具有线性相关关系的变量的相关性越强,则线性相关系数|r|的值越接近于 1
< ,σ >σ ,在同一直角坐标系中,X ,X 密度曲线的两个μ交点的横坐标为 x ,μ x ,且 x <x ,μ
2 1 2 1 2 1 2 1 2
C.若设直线回归方程为 ,则当变量 x 增加 1 个单位时, 平均增加 2 个单位
则μ( )
A.P(X < )<P(X < ) B.P(X <x )>P(X <x ) D.对具有线性相关关系的变量 x,y,其线性回归方程为 ,若样本点的中心为(m,2.8),
1 1 2 2 1 2 2 2
C.P(X
1
<xμ1 )>P(X
2
<xμ1 ) D.P(X
1
<
2
)<P(X
2
<
1
)
则实数 m 的值是﹣4.
μ μ
7.某学校在一次调查“篮球迷”的活动中,获得了如下数据:以下结论正确的是( )
10.已知函数 f(x)=x3﹣3x2,其导函数为 g(x),则( )
男生 女生 A.f(x)有两个极值点B.f(x)有三个互不相同的零点
篮球迷 30 15
第 1 页(共 2 页)C.方程 f(x)=a 有三个不同解,则实数 a 的取值范围为(﹣4,0)
D.g(2﹣x)=g(x)
11.已知数列{a }的前 n 项和 ,下列说法正确的是( )
n
A.a =2n+3
n
17.(本小题 15 分)已知函数 f(x)=x3+ax2﹣3x,a R,且满足 f′(1)=0.
B. 是公差为 1 的等差数列
∈
(1)求函数 f(x)的解析式;
C.数列{(﹣1)na }的前 2025 项和为﹣2023 (2)求函数 f(x)在区间 上的最大值与最小值.
n
D.数列 的前 n 项和
三、填空题:本题共 3 小题,每小题 5 分,共 15 分。 18.(本小题 17 分)某学校高二年级乒乓球社团举办了一次乒乓球比赛,进入决赛的 9 名选手来自于 3
个不同的班级,三个班级的选手人数分别是 2,3,4,本次决赛的比赛赛制采取单循环方式,即每名
12.若 (a 为正常数)的展开式中所有项的系数之和为 81,则展开式中的常数项为 .
选手进行 8 场比赛,每场比赛采取 5 局 3 胜制,先赢得三场的人为获胜者,比赛结束,根据积分选
13.为积极落实“双减”政策,丰富学生的课外活动,某校开设了航模、无人机、Ai 技术等 5 门课程.分
出最后的冠军.如果最终积分相同,则同分选手加赛决出排名,积分规则如下:比赛中以 3:0 或 3:
别安排在周一到周五,每天一节,其中 Ai 技术课不排在周一,航模和无人机课两天相邻的课程的安
1 取胜的选手积 3 分,失败的选手积 0 分;而在比赛中以 3:2 取胜的选手积 2 分,失败的选手积 1
排方案种数为 .
分.已知第 6 场是甲、乙之间的比赛,设每局比赛甲取胜的概率为 p(0<p<1).
14.若函数 f(x)=lnx﹣x﹣a 有两个零点,则 a 的取值范围是 .
(1)若进入决赛的 9 名选手获得冠亚军的概率相等,则比赛结束后冠亚军恰好来自同一个班级的概
四、解答题:本题共 5 小题,共 77 分。解答应写出必要的文字说明、证明过程或演算步骤。
率是多少?
15.(本小题 13 分)已知{a }是各项均为正数的等比数列,a =1,且 a ,3a ,a 成等差数列.
n 1 3 2 4
(2)在第 6 场比赛中,当 时,设甲所得积分为 X,求 X 的分布列及期望;
(1)求{a }的通项公式;
n
(2)设 b =a +log a ,求数列{b }的前 n 项和. (3)在第 6 场比赛中,记甲 3:1 取胜的概率为 f(p),求 f(p)的最大值.
n n 2 n n
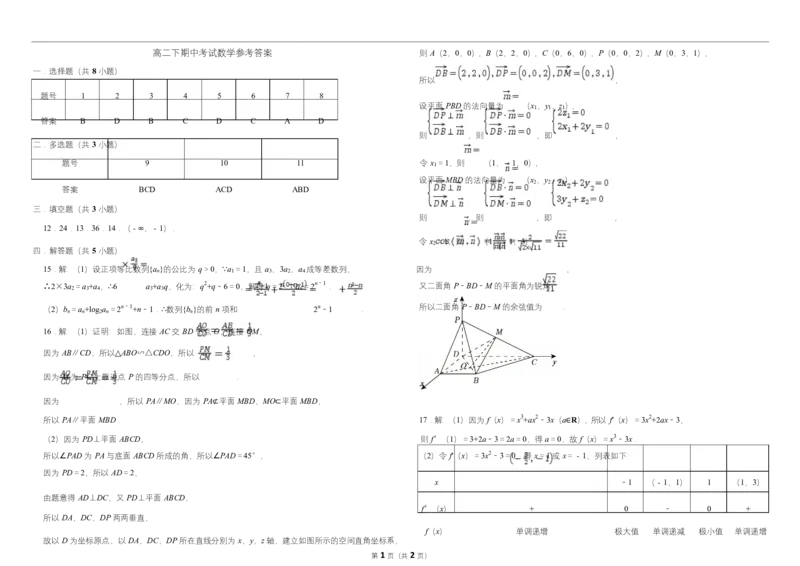
16.(本小题 15 分)如图,在四棱锥 P﹣ABCD 中,PD⊥平面 ABCD,AB∥DC,AB⊥AD,DC=3AB
=6,PD=2,点 M 在棱 PC 上.
19.(本小题 17 分)已知 A,B 分别为椭圆 C: 的左、右顶点, ,
(1)当 M 为 PC 上靠近点 P 的四等分点时,求证:PA∥平面 MBD;
M,N 均为椭圆 C 上异于顶点的点,H 为椭圆 C 上的点,直线 HM 经过左焦点 F ,直线 HN 经过
1
右 (2)若直线 PA 与平面 ABCD 所成的角为 45°,当 M 为 PC 的中点时,求二面角 P﹣BD﹣M 的余
焦点 F (1,0).
2
弦值.
(1)求椭圆 C 的标准方程.
(2)试问 是否为定值?若是定值,求出该定值;若不是,请说明理由.第 1 页(共 2 页)(3)设△HMN 的面积与△HF
1
F
2
的面积分别为 S△HMN , ,求 的最小值.
第 1 页(共 2 页)高二下期中考试数学参考答案 则 A(2,0,0),B(2,2,0),C(0,6,0),P(0,0,2),M(0,3,1),
一.选择题(共 8 小题)
所以 ,
题号 1 2 3 4 5 6 7 8
设平面 PBD 的法向量为 (x ,y ,z ),
1 1 1
答案 B D B C D C A D
则 ,则 ,即 ,
二.多选题(共 3 小题)
题号 9 10 11 令 x =1,则 (1,﹣1,0),
1
设平面 MBD 的法向量为 (x ,y ,z ),
2 2 2
答案 BCD ACD ABD
三.填空题(共 3 小题)
则 ,则 ,即 ,
12.24.13.36.14.(﹣∞,﹣1).
令 x =1,则 (1,﹣1,3),
2
四.解答题(共 5 小题)
15.解:(1)设正项等比数列{a }的公比为 q>0,∵a =1,且 a ,3a ,a 成等差数列, 因为 ,
n 1 3 2 4
∴2×3a =a +a ,∴6 a +a q,化为:q2+q﹣6=0,解得 q=2.∴a =2n﹣1. 又二面角 P﹣BD﹣M 的平面角为锐角,
2 3 4 3 3 n
(2)b =a +log a =2n﹣1+n﹣1.∴数列{b }的前 n 项和 2n﹣1 . 所以二面角 P﹣BD﹣M 的余弦值为 .
n n 2 n n
16.解:(1)证明:如图,连接 AC 交 BD 于点 O,连接 OM,
因为 AB∥CD,所以△ABO∽△CDO,所以 ,
因为 M 为 PC 上靠近点 P 的四等分点,所以 .
因为 ,所以 PA∥MO,因为 PA 平面 MBD,MO 平面 MBD,
所以 PA∥平面 MBD. ⊄ ⊂ 17.解:(1)因为 f(x)=x3+ax2﹣3x(a R),所以 f'(x)=3x2+2ax﹣3,
(2)因为 PD⊥平面 ABCD, 则 f′(1)=3+2a﹣3=2a=0,得 a=0,∈故 f(x)=x3﹣3x.
所以∠PAD 为 PA 与底面 ABCD 所成的角,所以∠PAD=45°, (2)令 f'(x)=3x2﹣3=0,得 x=1 或 x=﹣1,列表如下:
因为 PD=2,所以 AD=2,
x ﹣1 (﹣1,1) 1 (1,3)
由题意得 AD⊥DC,又 PD⊥平面 ABCD,
f′(x) + 0 ﹣ 0 +
所以 DA,DC,DP 两两垂直,
f(x) 单调递增 极大值 单调递减 极小值 单调递增
故以 D 为坐标原点,以 DA,DC,DP 所在直线分别为 x,y,z 轴,建立如图所示的空间直角坐标系,
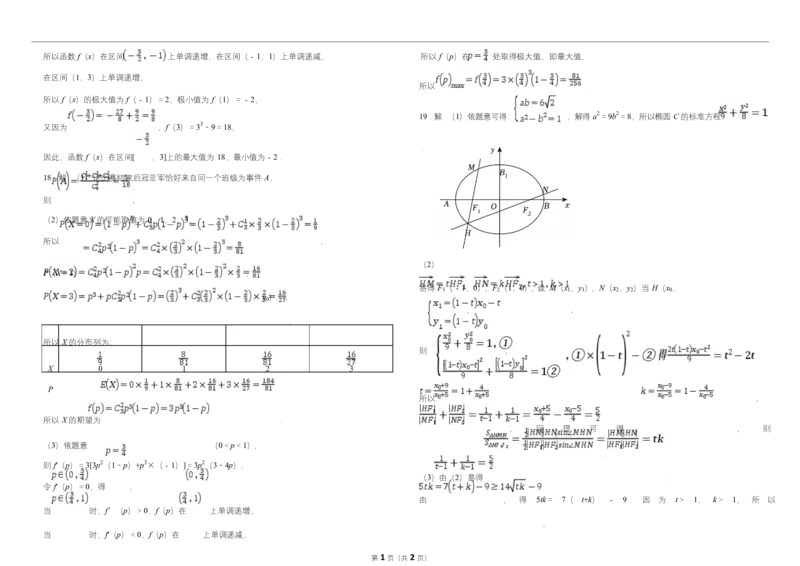
第 1 页(共 2 页)所以函数 f(x)在区间 上单调递增,在区间(﹣1,1)上单调递减, 所以 f(p)在 处取得极大值,即最大值,
在区间(1,3)上单调递增,
所以 .
所以 f(x)的极大值为 f(﹣1)=2,极小值为 f(1)=﹣2,
19.解:(1)依题意可得: ,解得 a2=9b2=8,所以椭圆 C 的标准方程
又因为 ,f(3)=33﹣9=18,
.
因此,函数 f(x)在区间[ ,3]上的最大值为 18,最小值为﹣2.
18.解:(1)记比赛结束后冠亚军恰好来自同一个班级为事件 A,
则 ;
(2)依题意 X 的可能取值为 0,1,2,3,
所以 ,
(2)
P(X=1) ,
易得 F (﹣1,0),F (1,0),设 M(x ,y ),N(x ,y )当 H(x ,
1 2 1 1 2 2 0
y ), ,
0
, ,
,
所以 X 的分布列为:
则 ,
X 0 1 2 3
P
所以 ,
所以 X 的期望为 .
, 同 理 可 得 , 则
(3)依题意 (0<p<1),
.
则 f'(p)=3[3p2(1﹣p)+p3×(﹣1)]=3p2(3﹣4p),
(3)由(2)易得 .
令 f'(p)=0,得 ,
由 , 得 5tk= 7( t+k) ﹣ 9. 因 为 t> 1, k> 1, 所 以
当 时,f′(p)>0,f(p)在 上单调递增,
,
当 时,f'(p)<0,f(p)在 上单调递减,
第 1 页(共 2 页)解得 或 tk≤1(舍去),当且仅当 时,等号成立,
故 的最小值为
声明:试题解析著作权属所有,未经书面同意,不得复制发布日期:2025/4/20 18:06:35;用户:王一森;邮箱:15149842802;学号:57458473
第 1 页(共 2 页)