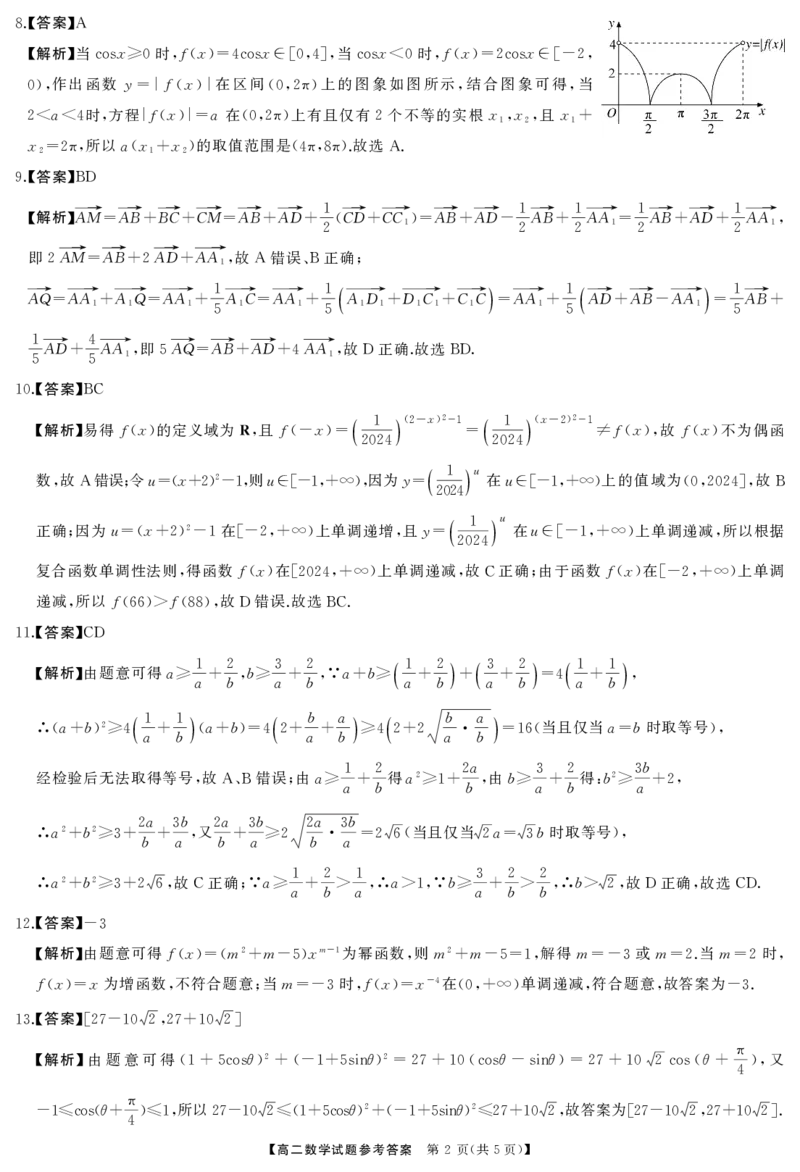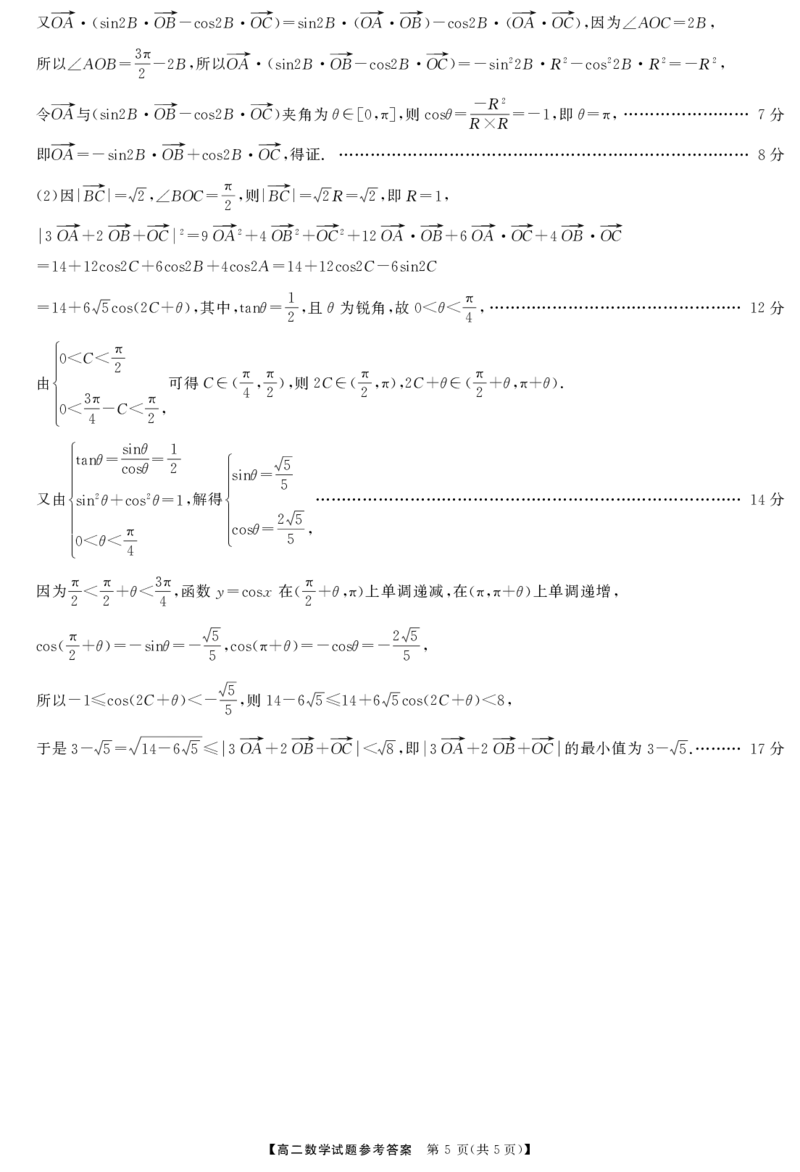数学答案-湖南名校联盟2024年高二9月入学考试_2024-2025高二（7-7月题库）_2024年09月试卷_0910湖南名校联盟2024年高二9月入学考试数学试题

参考答案、提示及评分细则 ．【答案】 １ B 【解析】因为a x b 且a b 所以 x 解得x ５ 故选 ． ＝(,１,２),＝(４,２,４), ⊥ , ４ ＋２＋８＝０, ＝－ , B ２ ．【答案】 ２ C 【解析】由对数不等式可得A x x 故A B 故选 ． ＝{|－１＜ ≤３}, ∩ ＝{２}, C ．【答案】 ３ B 【解析】因为空间向量p a b c以abc 为基底时的坐标为 且p q a b c 故 ＝２ －３ ＋３ {,,} (２,－３,３), ＋ ＝５ －２ ＋４ , p q以abc 为基底时的坐标为 故选 ． ＋ {,,} (５,－２,４), B ．【答案】 ４ B 【解析】样本数据的平均数x － ４８＋４９＋５０＋５０＋５０＋５０＋５１＋５２ ＝ ＝５０, ８ 方差s２ １ ２ ２ ２ ２ ２ ． 故选 ． ＝ ×[(４８－５０)＋(４９－５０)＋４×(５０－５０)＋(５１－５０)＋(５２－５０)]＝１２５, B ８ ．【答案】 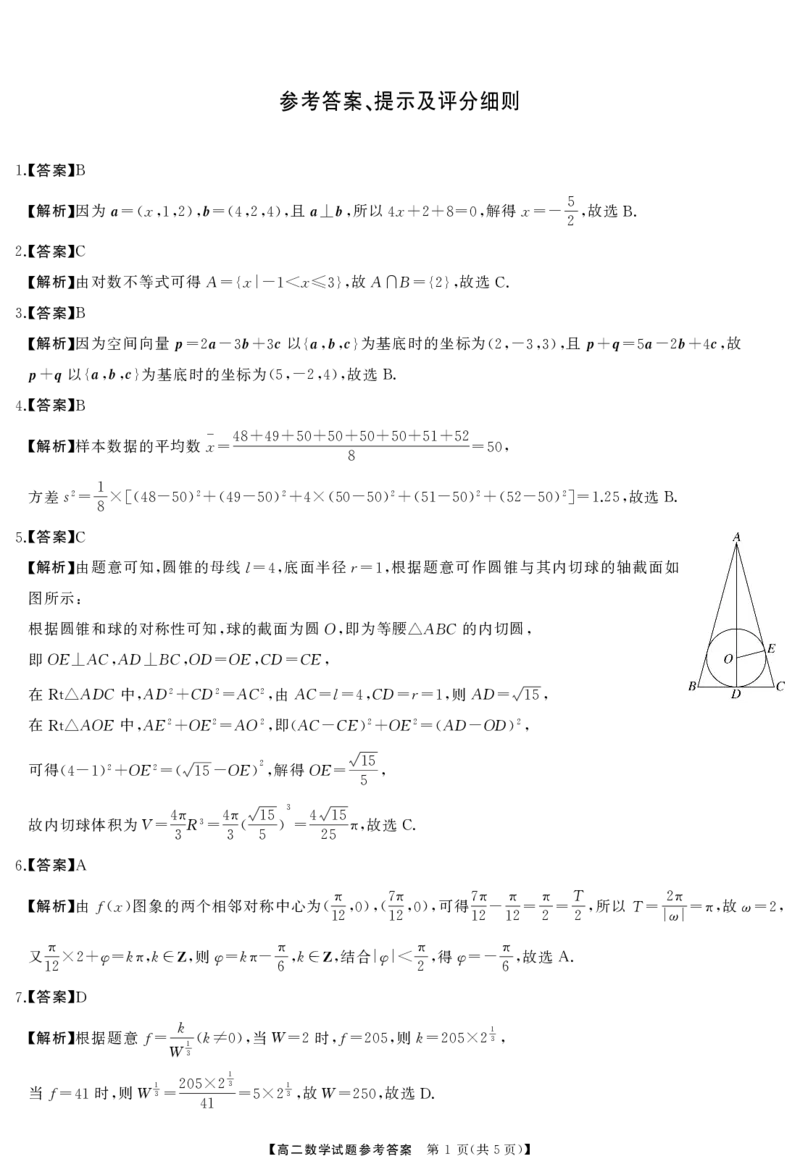５ C 【解析】由题意可知 圆锥的母线l 底面半径r 根据题意可作圆锥与其内切球的轴截面如 , ＝４, ＝１, 图所示 : 根据圆锥和球的对称性可知 球的截面为圆O 即为等腰 ABC的内切圆 , , △ , 即OE ACAD BCOD OECD CE ⊥ , ⊥ , ＝ , ＝ , 在 ADC中 AD２ CD２ AC２ 由AC l CD r 则AD Rt△ , ＋ ＝ , ＝ ＝４, ＝ ＝１, ＝ １５, 在 AOE中 AE２ OE２ AO２ 即 AC CE ２ OE２ AD OD ２ Rt△ , ＋ ＝ , ( － )＋ ＝( － ), 可得 ２ OE２ OE ２ 解得OE １５ (４－１)＋ ＝(１５－ ), ＝ , ５ ３ 故内切球体积为V ４πR３ ４π １５ ４ １５ 故选 ． ＝ ＝ ( )＝ π, C ３ ３ ５ ２５ ．【答案】 ６ A T 【解析】由fx 图象的两个相邻对称中心为 π ７π 可得７π π π 所以T ２π 故ω () ( ,０),( ,０), － ＝ ＝ , ＝ ω ＝π, ＝２, １２ １２ １２ １２ ２ ２ || 又π φ k k Z 则 φ k πk Z 结合 φ π 得 φ π 故选 ． ×２＋ ＝ π,∈ , ＝ π－ ,∈ , ||＜ , ＝－ , A １２ ６ ２ ６ ．【答案】 ７ D k 【解析】根据题意f k 当W 时f 则k １ ＝W１(≠０), ＝２ ,＝２０５, ＝２０５×２３, ３ １ 当f 时 则W１ ２０５×２３ １ 故W 故选 ． ＝４１ , ３＝ ＝５×２３, ＝２５０, D ４１ 高二数学试题参考答案 第 页 共 页 【 １ ( ５ )】 {{##{{QQQQAABBKKYYYa8U5oggggQgkAIJSBAACAbR5hrECwEFwICV4gCuQgCkJQEkhBJGWAgCESwgUGCBGEKAAA4ICAIgAQwNAINFIAAB=A}#A}=}#}．【答案】 ８ A 【解析】当 x 时fx x 当 x 时 fx x cos ≥０ ,()＝４cos ∈[０,４], cos ＜０ , ( )＝２cos ∈[－２, 作出函数y fx 在区间 上的图象如图所示 结合图象可得 当 ０), ＝| ( )| (０,２π) , , a 时 方程fx a在 上有且仅有 个不等的实根x x 且x ２＜ ＜４ , | ()|＝ (０,２π) ２ １,２, １＋ x 所以ax x 的取值范围是 ．故选 ． ２＝２π, (１＋ ２) (４π,８π) A ．【答案】 ９ BD 【解析】AM→ AB→ BC→ CM→ AB→ AD→ １ CD→ CC→ AB→ AD→ １AB→ １AA→ １AB→ AD→ １AA→ ＝ ＋ ＋ ＝ ＋ ＋ ( ＋ １)＝ ＋ － ＋ １＝ ＋ ＋ １, ２ ２ ２ ２ ２ 即 AM→ AB→ AD→ AA→ 故 错误 正确 ２ ＝ ＋２ ＋ １, A 、B ; ( ) ( ) AQ→ AA→ AQ→ AA→ １AC→ AA→ １ AD→ DC→ CC→ AA→ １ AD→ AB→ AA→ １AB→ ＝ １＋ １ ＝ １＋ １ ＝ １＋ １ １＋ １ １＋ １ ＝ １＋ ＋ － １ ＝ ＋ ５ ５ ５ ５ １AD→ ４AA→ 即 AQ→ AB→ AD→ AA→ 故 正确．故选 ． ＋ １, ５ ＝ ＋ ＋４ １, D BD ５ ５ ．【答案】 １０ BC 【解析】易得fx 的定义域为R 且f x ( １ ) (２－ x )２－１ ( １ ) ( x －２)２－１ fx 故fx 不为偶函 () , (－ )＝ ＝ ≠ ( ), ( ) ２０２４ ２０２４ ( )u 数 故 错误 令u x ２ 则u 因为y １ 在u 上的值域为 故 , A ; ＝(＋２)－１, ∈[－１,＋∞), ＝ ∈[－１,＋∞) (０,２０２４], B ２０２４ ( )u 正确 因为u x ２ 在 上单调递增 且y １ 在u 上单调递减 所以根据 ; ＝(＋２)－１ [－２,＋∞) , ＝ ∈[－１,＋∞) , ２０２４ 复合函数单调性法则 得函数fx 在 上单调递减 故 正确 由于函数fx 在 上单调 , () [２０２４,＋∞) , C ; () [－２,＋∞) 递减 所以f f 故 错误．故选 ． , (６６)＞ (８８), D BC ．【答案】 １１ CD ( ) ( ) ( ) 【解析】由题意可得a １ ２b ３ ２ a b １ ２ ３ ２ １ １ ≥a＋b,≥a＋b,∵ ＋ ≥ a＋b ＋ a＋b ＝４a＋b , ( ) ( b a) ( b a) a b２ １ １ a b 当且仅当a b时取等号 ∴(＋ )≥４a＋b (＋ )＝４２＋a＋b ≥４２＋２ a􀅰b ＝１６( ＝ ), a b 经检验后无法取得等号 故 错误 由a １ ２得a２ ２ 由b ３ ２得b２ ３ , A、B ; ≥a＋b ≥１＋b, ≥a＋b : ≥a＋２, a b a b a b a２ b２ ２ ３ 又２ ３ ２ ３ 当且仅当 a b时取等号 ∴ ＋ ≥３＋b＋a, b＋a≥２ b􀅰a ＝２６( ２ ＝ ３ ), a２ b２ 故 正确 a １ ２ １ a b ３ ２ ２ b 故 正确 故选 ． ∴ ＋ ≥３＋２６, C ;∵ ≥a＋b＞a,∴ ＞１,∵ ≥a＋b＞b,∴ ＞ ２, D , CD ．【答案】 １２ －３ 【解析】由题意可得fx m２ m xm －１ 为幂函数 则m２ m 解得m 或m ．当m 时 ()＝( ＋ －５) , ＋ －５＝１, ＝－３ ＝２ ＝２ , fx x为增函数 不符合题意 当m 时fx x－４ 在 单调递减 符合题意 故答案为 ． ()＝ , ; ＝－３ ,()＝ (０,＋∞) , , －３ ．【答案】 １３ [２７－１０２,２７＋１０２] 【解析】由题意可得 θ２ θ２ θ θ θ π 又 (１＋５cos )＋(－１＋５sin )＝２７＋１０(cos －sin )＝２７＋１０ ２cos( ＋ ), ４ θ π 所以 θ２ θ２ 故答案为 ． －１≤cos(＋ )≤１, ２７－１０２≤(１＋５cos)＋(－１＋５sin)≤２７＋１０２, [２７－１０２,２７＋１０２] ４ 高二数学试题参考答案 第 页 共 页 【 ２ ( ５ )】 {{##{{QQQQAABBKKYYYa8U5oggggQgkAIJSBAACAbR5hrECwEFwICV4gCuQgCkJQEkhBJGWAgCESwgUGCBGEKAAA4ICAIgAQwNAINFIAAB=A}#A}=}#}．【答案】 １４ ２３＋２２ 【解析】点P与点A 和点B 的距离之和为 x２ y２ z２ x ２ y２ z２ １(０,０,０) １(２,０,０) ＋ ＋ ＋ (－２)＋ ＋ 因为A 关于平面ABCD 的对称点为D 故PA PB DB 当且仅当P为DB 中点 即P为正方 １ １ １ , １＋ １≥ １＝２３, １ , 体中心时等号成立 点P与点M 和点N 的距离之和可表示为 x ２ y２ z ２ ; (１,０,２) (１,２,０) (－１)＋ ＋(－２)＋ x ２ y ２ z２ 则PM PN MN 当且仅当P在MN所在直线上时等号成立 (－１)＋(－２)＋ , ＋ ≥ ＝２２, , 故 x２ y２ z２ x ２ y２ z２ x ２ y２ z ２ x ２ y ２ z２ ＋ ＋ ＋ (－２)＋ ＋ ＋ (－１)＋ ＋(－２)＋ (－１)＋(－２)＋ 的最小值为 当且仅当P为正方体中心时等号成立 故答案为 ． ２３＋２２, , :２３＋２２ ．【解析】由题意可得AC→ xx x BC→ xx 分 １５ ＝(１－ ,－３,４－２ ), ＝(０,－ ,＋１), 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ３ 因为AC→ BC→ xx x xx x x x x 􀅰 ＝(１－ ,－３,４－２ )􀅰(０,－ ,＋１)＝ (３－ )＋(＋１)(４－２ )＝２, 解得x 或 １ 分 ＝２ － 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ７ ３ 由空间两点间的距离公式 (２) , 得 AB x２ x x ２ x x ２ x２ x ＝ (１－ )＋[(＋２)－(５－ )]＋[(２－ )－(２ －１)]＝ １４ －３２ ＋１９ ( )２ x ８ ５ 分 ＝ １４ － ＋ ,􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 １１ ７ ７ 当x ８时 AB 有最小值 ３５． 分 ＝ , 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 １３ ７ ７ a a a a a a ．【解析】 由题意可得z ＋i (＋i)(１＋i) (－１)＋(１＋ )i －１ １＋ 分 １６ (１) ＝ ＝ ＝ ＝ ＋ i,􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ５ １－i (１－i)(１＋i) ２ ２ ２ ì ïa －１ ïï ＝０ 因为z是纯虚数 所以í ２ 解得a ． 分 , ï , ＝１ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ８ a ïï１＋ î ≠０ ２ 由 得到z 又 １ ２ ３ ４ 分 (２) (１) ＝i, i＝i,i＝－１,i＝－i,i＝１,􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 １０ 则n ∈ N∗,i ４ n －３ ＝i,i ４ n －２ ＝－１,i ４ n －１ ＝i,i ４ n ＝１, 即有n ∈ N∗,i ４ n －３ ＋i ４ n －２ ＋i ４ n －１ ＋i ４ n ＝０,􀆺􀆺􀆺􀆺􀆺􀆺􀆺 １３ 分 故２０２５ zn z z２ z２０２５ ２ ３ ４ ． 分 n∑ ＝ ＋ ＋􀆺＋ ＝５０６(i＋i＋i＋i)＋i＝i 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 １５ ＝１ ．【解析】 设 甲解出该题 为事件A 乙解出该题 为事件B 丙解出该题 为事件C 则ABC相互独立 １７ :(１) “ ” ,“ ” ,“ ” , , , , 分 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 １ 由题意得PA ２ PAC PAPC ２ PC １ 分 ( )＝ , ( )＝ ( ) ( )＝ 􀅰 ( )＝ ,􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ３ ３ ３ ２ 所以PC ３ 分 ( )＝ , 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ４ ４ ( ) PBC PBPC PB PC PB ３ １ 分 (􀭺)＝ ( ) (􀭺)＝ ( )(１－ ( ))＝ ( )􀅰 １－ ＝ ,􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ６ ４ ８ 所以PB １ 分 ( )＝ , 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ７ ２ 所以乙 丙各自解出该题的概率为１ ３． 分 、 , 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ８ ２ ４ 设 甲 乙 丙 人中至少有 人解出该题 为事件D (２) “ 、 、 ３ １ ” , 高二数学试题参考答案 第 页 共 页 【 ３ ( ５ )】 {{##{{QQQQAABBKKYYYa8U5oggggQgkAIJSBAACAbR5hrECwEFwICV4gCuQgCkJQEkhBJGWAgCESwgUGCBGEKAAA4ICAIgAQwNAINFIAAB=A}#A}=}#}则D ABC 分 􀭿 ＝ 􀭿􀭺􀭺,􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ９ 因为PA ２ PB １ PC ３ ( )＝ , ( )＝ , ( )＝ , ３ ２ ４ 所以PA １ PB １ PC １ 分 (􀭿)＝ , (􀭺)＝ , (􀭺)＝ ,􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 １１ ３ ２ ４ 因为ABC相互独立 所以PD PD PABC PAPBPC 􀭿、􀭺、􀭺 , ( )＝１－ (􀭿)＝１－ (􀭿􀭺􀭺)＝１－ (􀭿) (􀭺) (􀭺) １ １ １ ２３． 分 ＝１－ × × ＝ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 １４ ３ ２ ４ ２４ 所以甲 乙 丙 人中至少有 人解出该题的概率为２３． 分 、 、 ３ １ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 １５ ２４ ．【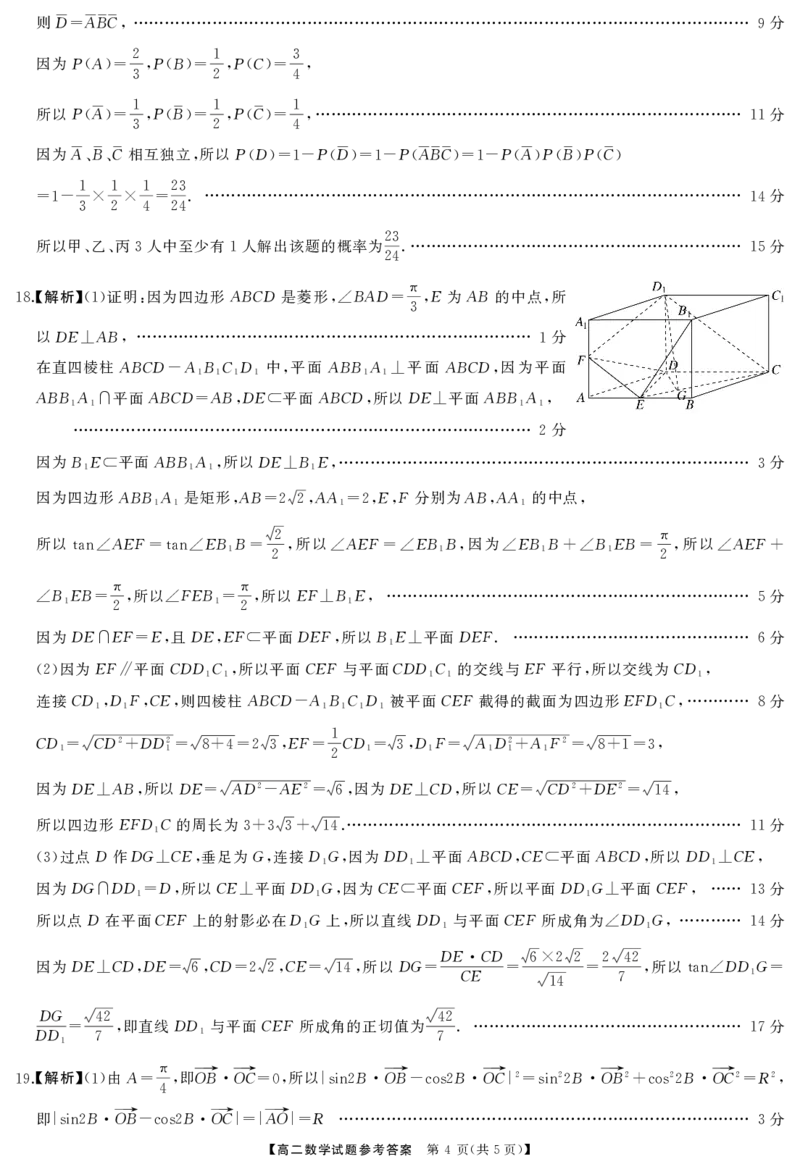解析】 证明 因为四边形ABCD是菱形 BAD π E为AB的中点 所 １８ (１) : ,∠ ＝ , , ３ 以DE AB 分 ⊥ ,􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 １ 在直四棱柱ABCD ABCD 中 平面ABBA 平面ABCD 因为平面 － １ １ １ １ , １ １⊥ , ABBA 平面ABCD ABDE 平面ABCD 所以DE 平面ABBA １ １∩ ＝ , ⊂ , ⊥ １ １, 分 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ２ 因为BE 平面ABBA 所以DE BE 分 １ ⊂ １ １, ⊥ １ ,􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ３ 因为四边形ABBA 是矩形 AB AA EF分别为ABAA 的中点 １ １ , ＝２２, １＝２, , , １ , 所以 AEF EBB ２ 所以 AEF EBB 因为 EBB BEB π 所以 AEF tan∠ ＝tan∠ １ ＝ , ∠ ＝∠ １ , ∠ １ ＋∠ １ ＝ , ∠ ＋ ２ ２ BEB π 所以 FEB π 所以EF BE 分 ∠ １ ＝ , ∠ １＝ , ⊥ １ , 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ５ ２ ２ 因为DE EF E 且DEEF 平面DEF 所以BE 平面DEF． 分 ∩ ＝ , , ⊂ , １ ⊥ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ６ 因为EF 平面CDDC 所以平面CEF与平面CDDC 的交线与EF平行 所以交线为CD (２) ∥ １ １, １ １ , １, 连接CD DFCE 则四棱柱ABCD ABCD 被平面CEF截得的截面为四边形EFDC 分 １, １ , , － １ １ １ １ １ ,􀆺􀆺􀆺􀆺 ８ CD CD２ DD２ EF １CD DF AD２ AF２ １＝ ＋ １＝ ８＋４＝２３, ＝ １＝ ３, １ ＝ １ １＋ １ ＝ ８＋１＝３, ２ 因为DE AB 所以DE AD２ AE２ 因为DE CD 所以CE CD２ DE２ ⊥ , ＝ － ＝ ６, ⊥ , ＝ ＋ ＝ １４, 所以四边形EFDC的周长为 ． 分 １ ３＋３３＋ １４ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 １１ 过点D作DG CE 垂足为G 连接DG 因为DD 平面ABCDCE 平面ABCD 所以DD CE (３) ⊥ , , １ , １⊥ , ⊂ , １⊥ , 因为DG DD D 所以CE 平面DDG 因为CE 平面CEF 所以平面DDG 平面CEF 分 ∩ １＝ , ⊥ １ , ⊂ , １ ⊥ , 􀆺􀆺 １３ 所以点D在平面CEF上的射影必在DG上 所以直线DD 与平面CEF所成角为 DDG 分 １ , １ ∠ １ ,􀆺􀆺􀆺􀆺 １４ DE CD 因为DE CDDE CD CE 所以DG 􀅰 ６×２２ ２ ４２ 所以 DDG ⊥ , ＝ ６, ＝２２, ＝ １４, ＝ CE ＝ ＝ , tan∠ １ ＝ １４ ７ DG ４２ 即直线DD 与平面CEF所成角的正切值为 ４２． 分 DD ＝ , １ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 １７ １ ７ ７ ．【解析】 由A π 即OB→ OC→ 所以 B OB→ B OC→ ２ ２B OB→２ ２B OC→２ R２ １９ (１) ＝ , 􀅰 ＝０, |sin２ 􀅰 －cos２ 􀅰 |＝sin２ 􀅰 ＋cos２ 􀅰 ＝ , ４ 即 B OB→ B OC→ AO→ R 分 |sin２ 􀅰 －cos２ 􀅰 |＝| |＝ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ３ 高二数学试题参考答案 第 页 共 页 【 ４ ( ５ )】 {{##{{QQQQAABBKKYYYa8U5oggggQgkAIJSBAACAbR5hrECwEFwICV4gCuQgCkJQEkhBJGWAgCESwgUGCBGEKAAA4ICAIgAQwNAINFIAAB=A}#A}=}#}又OA→ B OB→ B OC→ B OA→ OB→ B OA→ OC→ 因为 AOC B 􀅰(sin２ 􀅰 －cos２ 􀅰 )＝sin２ 􀅰( 􀅰 )－cos２ 􀅰( 􀅰 ), ∠ ＝２ , 所以 AOB ３π B 所以OA→ B OB→ B OC→ ２B R２ ２B R２ R２ ∠ ＝ －２ , 􀅰(sin２ 􀅰 －cos２ 􀅰 )＝－sin２ 􀅰 －cos２ 􀅰 ＝－ , ２ R２ 令OA→与 B OB→ B OC→ 夹角为θ 则 θ － 即θ 分 (sin２ 􀅰 －cos２ 􀅰 ) ∈[０,π], cos＝R R＝－１, ＝π,􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ７ × 即OA→ B OB→ B OC→ 得证． 分 ＝－sin２ 􀅰 ＋cos２ 􀅰 , 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ８ 因 BC→ BOC π 则 BC→ R 即R (２) | |＝ ２,∠ ＝ , | |＝ ２ ＝ ２, ＝１, ２ OA→ OB→ OC→ ２ OA→２ OB→２ OC→２ OA→ OB→ OA→ OC→ OB→ OC→ ３ ＋２ ＋ ＝９ ＋４ ＋ ＋１２ 􀅰 ＋６ 􀅰 ＋４ 􀅰 C B A C C ＝１４＋１２cos２ ＋６cos２ ＋４cos２ ＝１４＋１２cos２ －６sin２ C θ 其中 θ １ 且θ为锐角 故 θ π 分 ＝１４＋６５cos(２ ＋ ), ,tan ＝ , , ０＜ ＜ ,􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 １２ ２ ４ ì ï C π ïï０＜ ＜ 由í ２ 可得C π π 则 C π C θ π θ θ ． ï ∈( , ), ２ ∈( ,π),２ ＋ ∈( ＋ ,π＋ ) ４ ２ ２ ２ ïï ３π C π î０＜ － ＜ , ４ ２ ì ï θ ïtan θ ＝ sin θ＝ １ ì ï ïï cos ２ ï ïsin θ ＝ ５ 又由í ïsin ２θ ＋cos ２θ ＝１, 解得í ï ５ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 １４ 分 ï ï ï θ ２５ ïï θ π îcos＝ , î０＜ ＜ ５ ４ 因为π π θ ３π 函数y x在 π θ 上单调递减 在 θ 上单调递增 ＜ ＋ ＜ , ＝cos ( ＋ ,π) , (π,π＋ ) , ２ ２ ４ ２ π θ θ ５ θ θ ２５ cos( ＋ )＝－sin ＝－ ,cos(π＋ )＝－cos＝－ , ２ ５ ５ 所以 C θ ５ 则 C θ －１≤cos(２ ＋ )＜－ , １４－６５≤１４＋６５cos(２ ＋ )＜８, ５ 于是 OA→ OB→ OC→ 即 OA→ OB→ OC→ 的最小值为 ． 分 ３－ ５＝ １４－６５≤ ３ ＋２ ＋ ＜ ８, ３ ＋２ ＋ ３－ ５ 􀆺􀆺􀆺 １７ 高二数学试题参考答案 第 页 共 页 【 ５ ( ５ )】 {{##{{QQQQAABBKKYYYa8U5oggggQgkAIJSBAACAbR5hrECwEFwICV4gCuQgCkJQEkhBJGWAgCESwgUGCBGEKAAA4ICAIgAQwNAINFIAAB=A}#A}=}#}