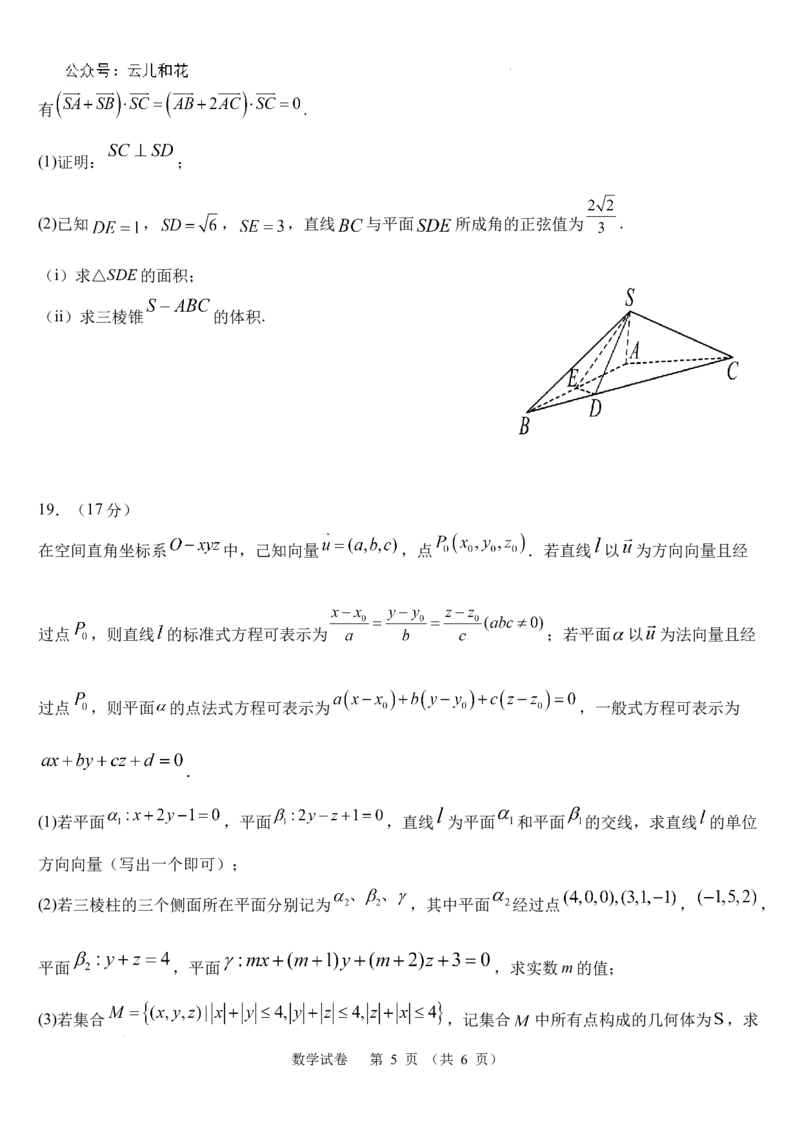文档内容
2024~2025学年第一学期福建省部分学校教学联盟高中入学适应性检测
高中二年级数学试卷
(考试时间:120分钟;满分:150分)
注意事项:
1.答题前,请考生认真检查试题卷有无缺印、漏印等问题。本卷共4页,19小题。
2.答题时,选择题部分用2B铅笔规范填涂。非选择题部分用0.5毫米黑色签字笔在答题卡上书写作
答。在试题卷上答题无效。
学校: 姓名: 准考证号:
一、单项选择题:本题共8小题,每小题5分,共40分。在每小题所给出的四个选项中,只有一个选
项是符合题目要求的。
1.在空间直角坐标系中,点 关于x轴对称的点坐标是( )
A. B. C. D.
2.已知 , ,且 ,则 的值为( )
A.6 B.10 C.12 D.14
3.在△ABC中,三个内角 的对边分别是 ,若 ,则 ( )
A. B. C. D. .
4.已知点 , , ,若A,B,C三点共线,则a,b的值分别是( )
A. ,3 B. ,2 C.1,3 D. ,2
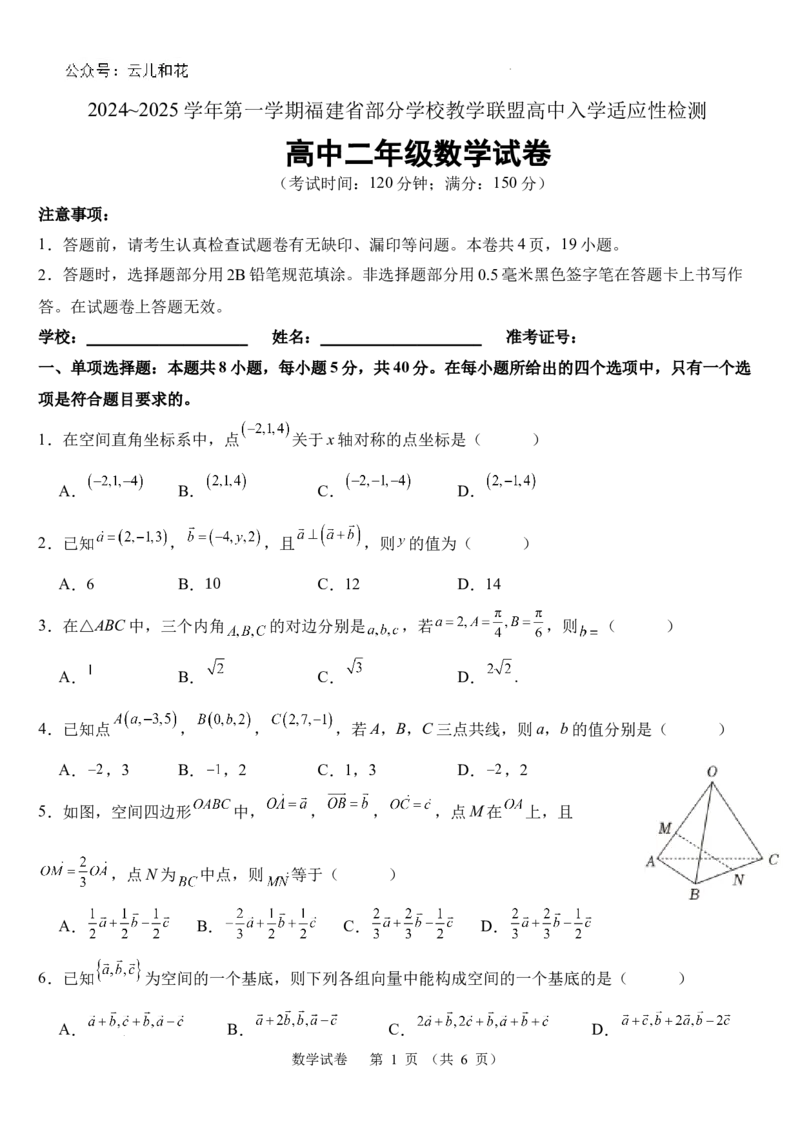
5.如图,空间四边形 中, , , ,点M在 上,且
,点N为 中点,则 等于( )
A. B. C. D.
6.已知 为空间的一个基底,则下列各组向量中能构成空间的一个基底的是( )
A. B. C. D.
数学试卷 第 1 页 (共 6 页)
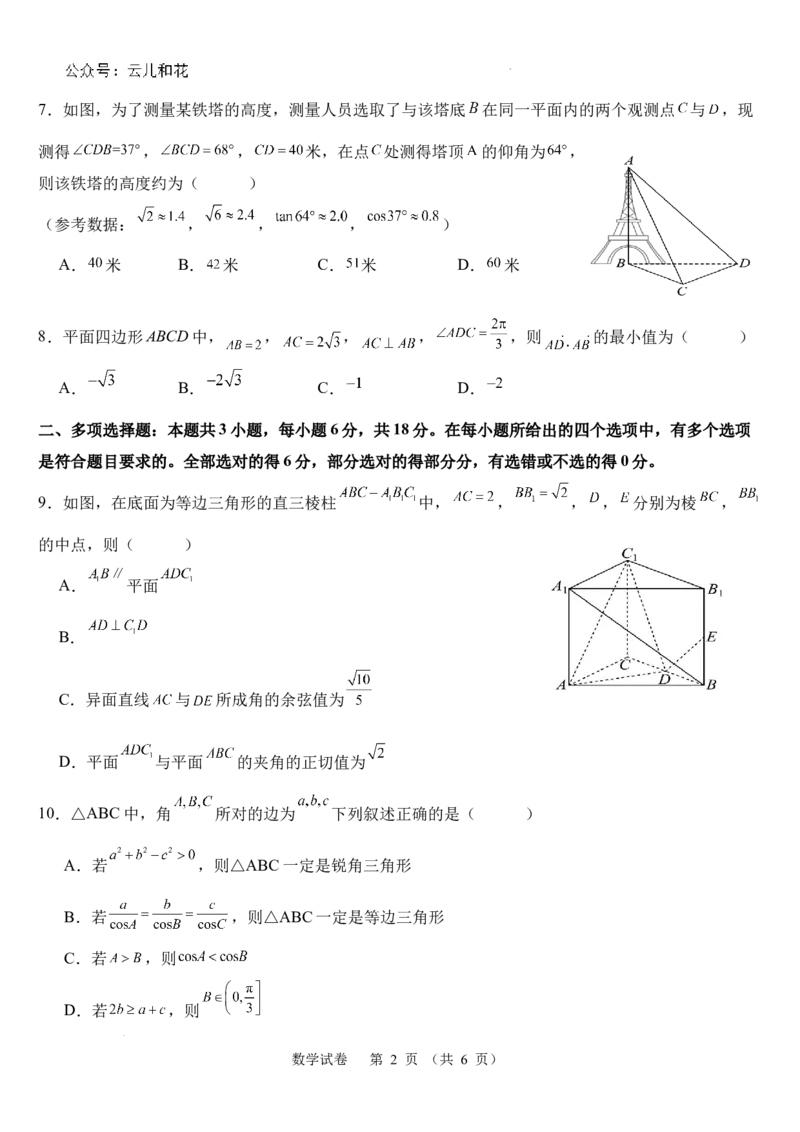
学科网(北京)股份有限公司7.如图,为了测量某铁塔的高度,测量人员选取了与该塔底 在同一平面内的两个观测点 与 ,现
测得 , , 米,在点 处测得塔顶 的仰角为 ,
则该铁塔的高度约为( )
(参考数据: , , , )
A. 米 B. 米 C. 米 D. 米
8.平面四边形ABCD中, , , , ,则 的最小值为( )
A. B. C. D.
二、多项选择题:本题共3小题,每小题6分,共18分。在每小题所给出的四个选项中,有多个选项
是符合题目要求的。全部选对的得6分,部分选对的得部分分,有选错或不选的得0分。
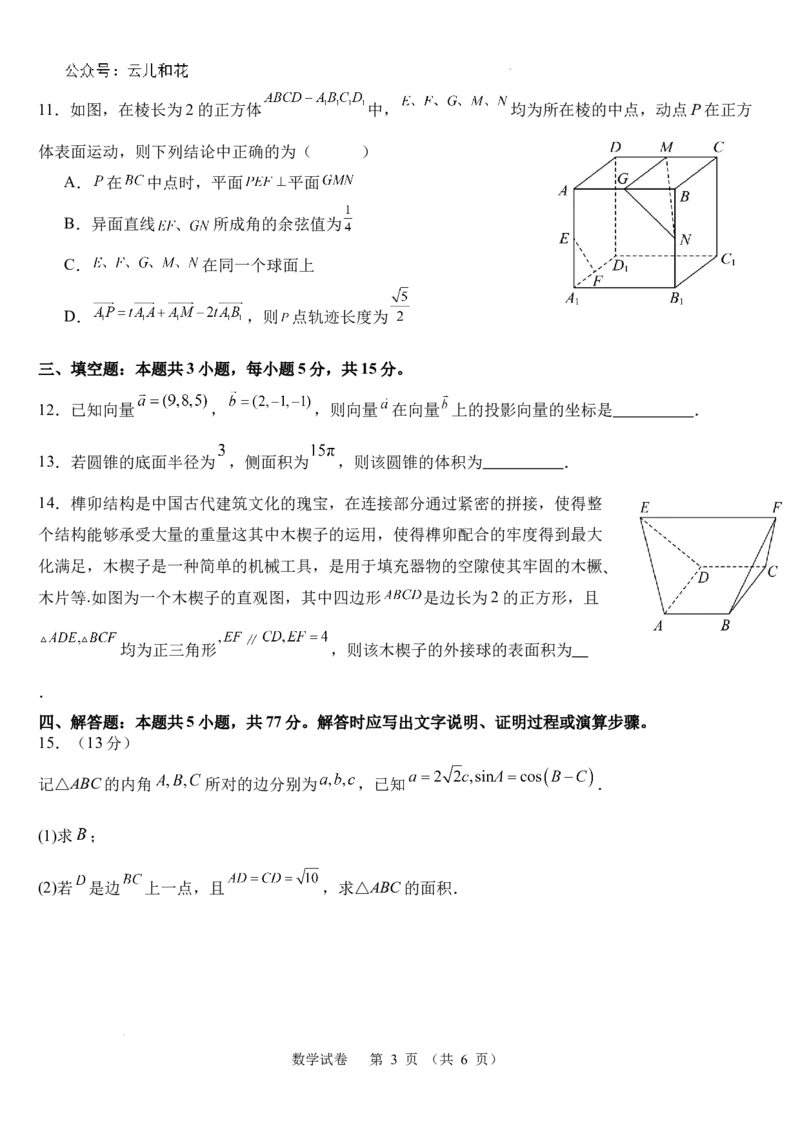
9.如图,在底面为等边三角形的直三棱柱 中, , , , 分别为棱 ,
的中点,则( )
A. 平面
B.
C.异面直线 与 所成角的余弦值为
D.平面 与平面 的夹角的正切值为
10.△ABC中,角 所对的边为 下列叙述正确的是( )
A.若 ,则△ABC一定是锐角三角形
B.若 ,则△ABC一定是等边三角形
C.若 ,则
D.若 ,则
数学试卷 第 2 页 (共 6 页)
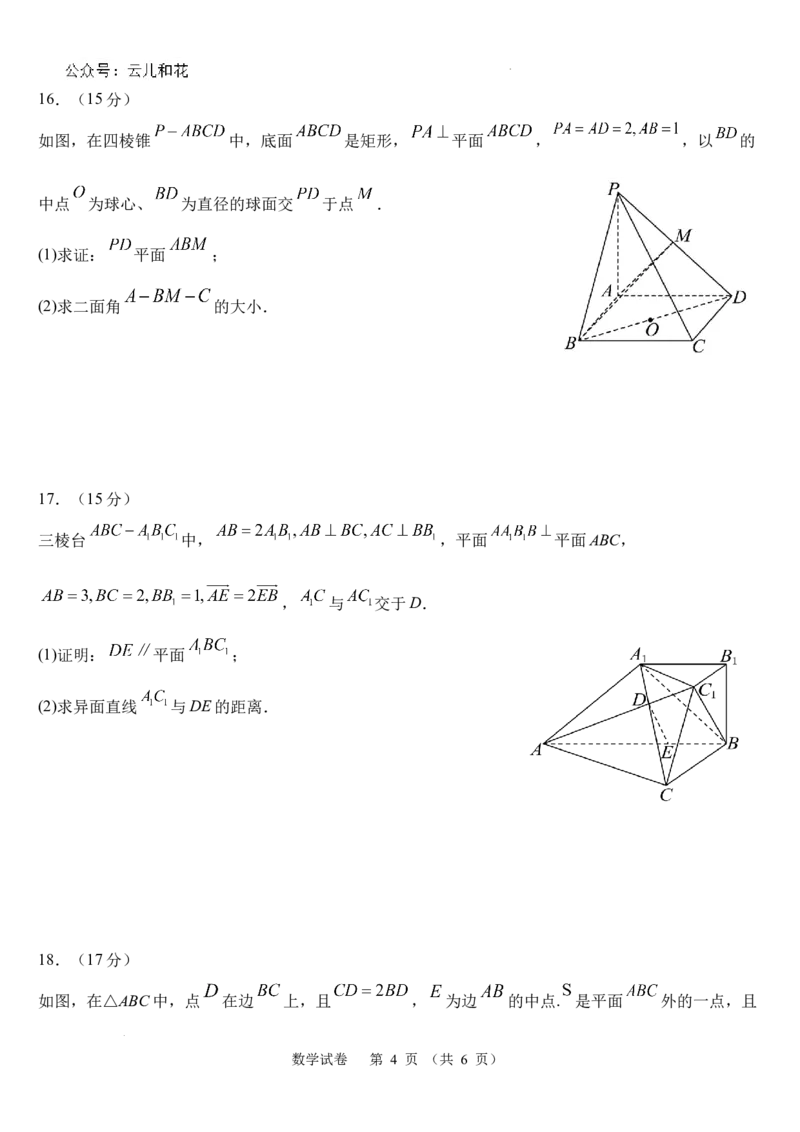
学科网(北京)股份有限公司11.如图,在棱长为2的正方体 中, 均为所在棱的中点,动点P在正方
体表面运动,则下列结论中正确的为( )
A. 在 中点时,平面 平面
B.异面直线 所成角的余弦值为
C. 在同一个球面上
D. ,则 点轨迹长度为
三、填空题:本题共3小题,每小题5分,共15分。
12.已知向量 , ,则向量 在向量 上的投影向量的坐标是 .
13.若圆锥的底面半径为 ,侧面积为 ,则该圆锥的体积为 .
14.榫卯结构是中国古代建筑文化的瑰宝,在连接部分通过紧密的拼接,使得整
个结构能够承受大量的重量这其中木楔子的运用,使得榫卯配合的牢度得到最大
化满足,木楔子是一种简单的机械工具,是用于填充器物的空隙使其牢固的木橛、
木片等.如图为一个木楔子的直观图,其中四边形 是边长为2的正方形,且
均为正三角形 ,则该木楔子的外接球的表面积为
.
四、解答题:本题共5小题,共77分。解答时应写出文字说明、证明过程或演算步骤。
15.(13分)
记△ABC的内角 所对的边分别为 ,已知 .
(1)求 ;
(2)若 是边 上一点,且 ,求△ABC的面积.
数学试卷 第 3 页 (共 6 页)
学科网(北京)股份有限公司16.(15分)
如图,在四棱锥 中,底面 是矩形, 平面 , ,以 的
中点 为球心、 为直径的球面交 于点 .
(1)求证: 平面 ;
(2)求二面角 的大小.
17.(15分)
三棱台 中, ,平面 平面ABC,
, 与 交于D.
(1)证明: 平面 ;
(2)求异面直线 与DE的距离.
18.(17分)
如图,在△ABC中,点 在边 上,且 , 为边 的中点. 是平面 外的一点,且
数学试卷 第 4 页 (共 6 页)
学科网(北京)股份有限公司有 .
(1)证明: ;
(2)已知 , , ,直线 与平面 所成角的正弦值为 .
(i)求△SDE的面积;
(ii)求三棱锥 的体积.
19.(17分)
在空间直角坐标系 中,己知向量 ,点 .若直线 以 为方向向量且经
过点 ,则直线 的标准式方程可表示为 ;若平面 以 为法向量且经
过点 ,则平面 的点法式方程可表示为 ,一般式方程可表示为
.
(1)若平面 ,平面 ,直线 为平面 和平面 的交线,求直线 的单位
方向向量(写出一个即可);
(2)若三棱柱的三个侧面所在平面分别记为 ,其中平面 经过点 , ,
平面 ,平面 ,求实数m的值;
(3)若集合 ,记集合 中所有点构成的几何体为 ,求
数学试卷 第 5 页 (共 6 页)
学科网(北京)股份有限公司几何体 的体积和相邻两个面(有公共棱)所成二面角的大小.
数学试卷 第 6 页 (共 6 页)
学科网(北京)股份有限公司