文档内容
高二数学
满分:150分 考试时间:120分钟
注意事项:
1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在考生信息条
形码粘贴区.
2.选择题必须使用 2B铅笔填涂;非选择题必须使用 0.5毫米黑色字迹签字笔书写,字体工
整、笔迹清晰.
3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在
草稿纸、试卷上答题无效.
4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑.
5.保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀.
一、选择题:本题共 8小题,每小题 5分,共 40分.在每小题给出的四个选项中,只有一项
是符合题目要求的.
{ } { }
A= x −1≤ x≤4 B= x lnx<2 AB =
1. 已知集合 , ,则 ( )
A. { x −1≤ x≤4 } B. { x 0< x2 D. a>4
6. 正六边形六个顶点中任取四个点,构成等腰梯形的概率是( )
第1页/共4页
学科网(北京)股份有限公司1 1 1 2
A. B. C. D.
10 5 3 5
7. f ( x ) 是定义在R上的函数,若 f ( 0 )=1,且对任意x∈R,满足 f ( x+2 )≤ f ( x )+2,
f ( x+8 )≥ f ( x )+8,则 f ( 2024 )=( )
A. 2023 B. 2024 C. 2025 D. 2026
1 1 24
+ =
8. 已知 α α 7 ,α∈( 0,π ) ,则cos2α=( )
sin cos
2 2
17 17 79 79
A. B. − C. D. −
81 81 128 128
二、选择题:本题共 3小题,每小题 6分,共 18分.在每小题给出的选项中,有多项符合题
目要求.全部选对的得 6分,部分选对的得部分分,有选错的得 0分.
9. 对于随机事件A和事件B,P
(
A
)=0.3,P (
B
)=0.4,则下列说法正确的是(
)
A. 若A与B互斥,则P ( AB )=0.3 B. 若A与B互斥,则P ( A∪B )=0.7
C. 若A与B相互独立,则P ( AB )=0.12 D. 若A与B相互独立,则P ( A∪B )=0.7
10. 已知正数a,b满足4a+b+ab=12,则下列结论正确的是( )
A. ab的最大值为4 B. 4a+b的最小值为8
1 1 3
C. a+b的最小值为3 D. + 的最小值
a+1 b 4
π
11. 在菱形ABCD中,边长为4 3,∠BAD= ,将△ABD沿对角线BD折起得到四面体ABCD,记
3
二面角A−BD−C的大小为θ(0<θ<π),则下列结论正确的是( )
A. 对任意θ,都有AC⊥BD
B. 存在θ,使AC ⊥平面ABD
2π π
C. 当θ= 时,直线AC与平面ABD所成角为
3 6
π 208π
D. 当θ= 时,四面体ABCD外接球表面积为
3 3
三、填空题:本题共 3小题,每小题 5分,共 15分.
12. 天然气是洁净燃气,供应稳定,能够改善空气质量,因而能为地区经济发展提供新的动力,带动经济
繁荣及改善环境.多年来,我国规模以上工业天然气生产稳定增长,2023年5月至2024年4月,天然气
日均产量(单位:亿立方米)依次为6.1,6.1,5.9,5.8,6.0,6.1,6.6,6.7,6.9,7.0,6.6,6.5,这组数
据的上四分位数是______.
第2页/共4页
学科网(北京)股份有限公司2π
13. 将函数 f ( x )=cos ( 2x+φ ) 的图象向右平移 后得到的图象关于原点对称,则ϕ的最小正值为
3
______.
x x
14. 若用x表示不大于x的最大整数,用x表示不小于x的最小整数,那么方程 = +5的最大
2 3
整数解为______.
四、解答题:本题共 5小题,共 77分.解答应写出文字说明、证明过程或演算步骤.
15. 为推动安徽省乡村旅游发展提质增效,更好满足人民群众旅游消费升级需求,助力乡村全面振兴,安
徽省实施精品示范工程打造“皖美休闲旅游乡村”行动方案,实施“微创意、微改造”,促进“精提升”,建设
“皖美”乡村新风景,打造全国知名的乡村旅游目的地.某学校兴趣小组同学利用暑假时间,在全省范围内
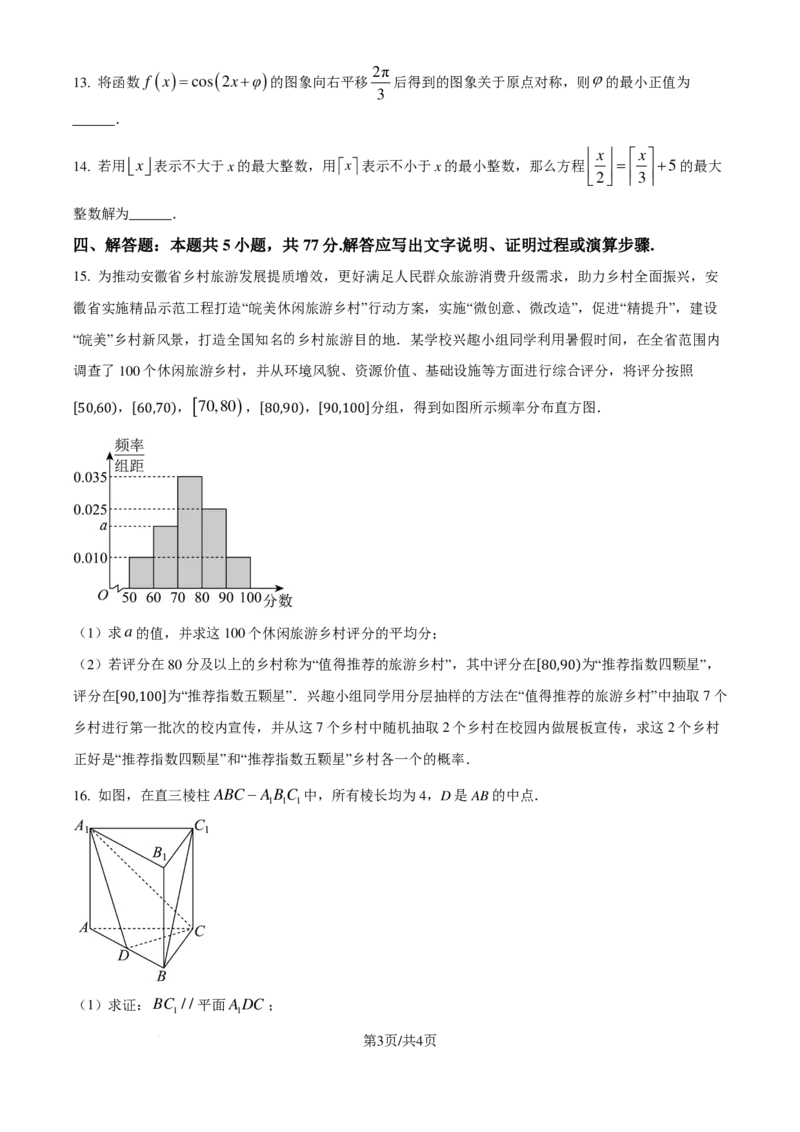
调查了100个休闲旅游乡村,并从环境风貌、资源价值、基础设施等方面进行综合评分,将评分按照
[ )
, , 70,80 , , 分组,得到如图所示频率分布直方图.
[50,60) [60,70) [80,90) [90,100]
(1)求a的值,并求这100个休闲旅游乡村评分的平均分;
(2)若评分在80分及以上的乡村称为“值得推荐的旅游乡村”,其中评分在 为“推荐指数四颗星”,
评分在 为“推荐指数五颗星”.兴趣小组同学用分层抽样的方法在“值[得80推,9荐0)的旅游乡村”中抽取7个
乡村进[行90第,1一00批] 次的校内宣传,并从这7个乡村中随机抽取2个乡村在校园内做展板宣传,求这2个乡村
正好是“推荐指数四颗星”和“推荐指数五颗星”乡村各一个的概率.
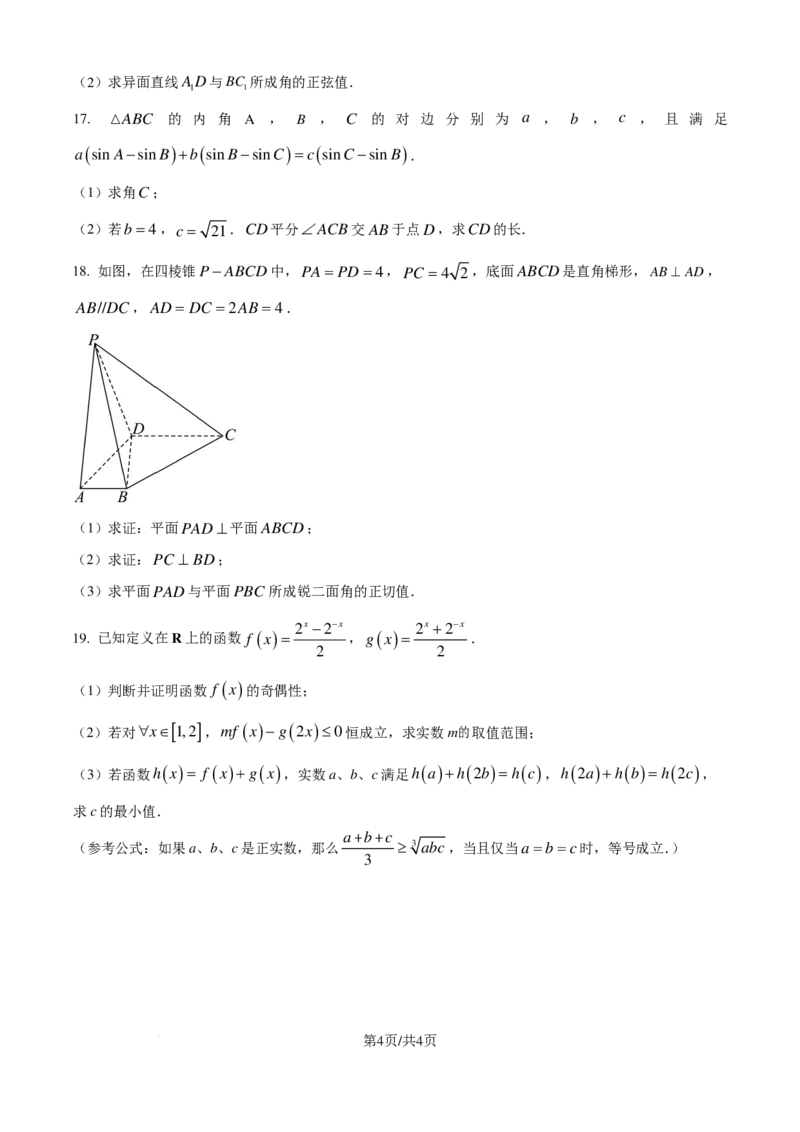
16. 如图,在直三棱柱ABC−ABC 中,所有棱长均为4,D是AB的中点.
1 1 1
(1)求证:BC //平面ADC;
1 1
第3页/共4页
学科网(北京)股份有限公司(2)求异面直线AD与BC 所成角的正弦值.
1 1
17. ABC 的 内 角 A , B , C 的 对 边 分 别 为 a , b , c , 且 满 足
a ( sinA−sinB )+b ( sinB−sinC )=c ( sinC−sinB ) .
(1)求角C;
(2)若b=4,c= 21.CD平分∠ACB交AB于点D,求CD的长.
18. 如图,在四棱锥P−ABCD中,PA= PD=4,PC =4 2,底面ABCD是直角梯形,AB⊥ AD,
AB//DC,AD= DC =2AB=4.
(1)求证:平面PAD⊥平面ABCD;
(2)求证:PC ⊥ BD;
(3)求平面PAD与平面PBC 所成锐二面角的正切值.
2x −2−x 2x +2−x
19. 已知定义在R上的函数 f ( x )= ,g ( x )= .
2 2
( )
(1)判断并证明函数 f x 的奇偶性;
(2)若对∀x∈[
1,2
]
,mf
(
x
)−g (
2x
)≤0恒成立,求实数m的取值范围;
(3)若函数h
(
x
)=
f
(
x
)+g (
x
)
,实数a、b、c满足h
(
a
)+h (
2b
)=h (
c
)
,h
(
2a
)+h (
b
)=h (
2c
)
,
求c的最小值.
abc
(参考公式:如果a、b、c是正实数,那么 3 abc,当且仅当a=b=c时,等号成立.)
3
第4页/共4页
学科网(北京)股份有限公司