文档内容
完成时间: 月 日 天气:
作业 01 三角函数的图象与性质
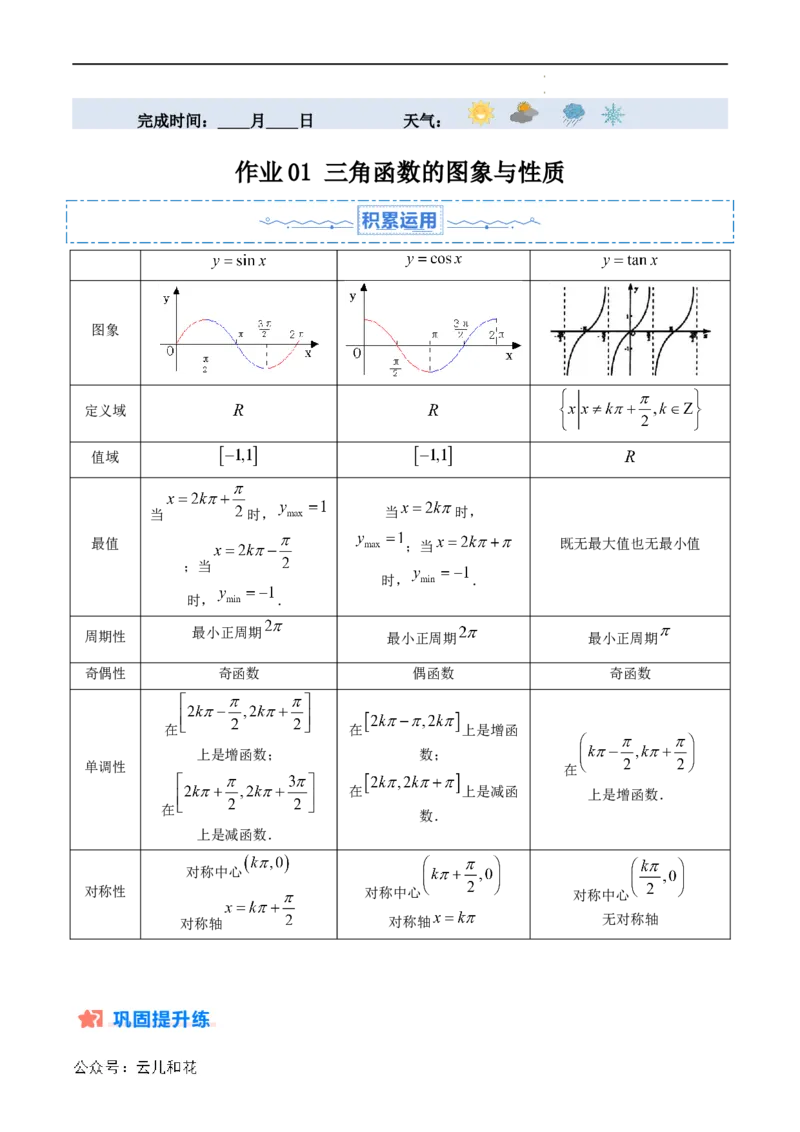
图象
定义域
值域
当 时, 当 时,
最值 ;当 既无最大值也无最小值
;当
时, .
时, .
周期性 最小正周期 最小正周期 最小正周期
奇偶性 奇函数 偶函数 奇函数
在 在 上是增函
上是增函数; 数;
单调性 在
在 上是减函 上是增函数.
在
数.
上是减函数.
对称中心
对称性 对称中心 对称中心
对称轴 对称轴 无对称轴
学科网(北京)股份有限公司一、单选题
1.函数 的最小正周期为( )
A. B. C.2 D.4
2.函数 的对称中心为( )
A. B. C. D.
3.已知函数 的部分图象如图所示,则( )
A. , B. ,
C. , D. ,
4.不等式 的解集为( )
A. B.
C. D.
5.设函数 在区间 上是单调函数, ,则
( )
A. B. C. D.
二、多选题
6.已知函数 (其中 )的部分图象如图所示,则下列结论正确的是
( )
学科网(北京)股份有限公司A.函数 的周期为
B.函数 的图象关于 对称
C.函数 在区间 上的最大值为2
D.直线 与 的图象所有交点的横坐标之和为
7.若函数 在 上单调,则 的取值可能为( )
A. B. C. D.
8.已知函数 ,则( )
A. 的对称轴为
B. 的最小正周期为
C. 的最大值为1,最小值为
D. 在 上单调递减,在 上单调递增
三、填空题
9.已知函数 ,且 在区间 上的最大值为 ,则 的最小值为 .
10.函数 的值域为 .
四、解答题
学科网(北京)股份有限公司11.已知函数 .
(1)求函数 的最小正周期和对称中心;
(2)求函数 的单调递减区间;
(3)当 时,求函数 的最值及此时x的值.
12.函数 的部分图像如图所示.
(1)求 的解析式;
(2)若 ,求 的值;
(3)若 恒成立,求 的取值范围.
1.函数 的单调递增区间为( )
A. B.
C. D.
2.已知函数 .若 在区间 内没有零点,则 的取值范围是
( )
A. B.
C. D.
3.(多选)已知函数 ,则( )
学科网(北京)股份有限公司A. 是奇函数 B. 是周期函数
C. D. 在区间 内单调递增
4.已知三角函数 ,又已知函数 满足如下条件 为 的一
个零点, 为 的一条对称轴,且 在区间 上单调.则 的最大值为
5.已知函数 ,满足
(1)求 的值
(2)若存在 ,使得等式 成立,求实数 的取值范围;
(3)若对任意 都有 恒成立,求实数 的取值范围.
1.已知函数 ,现给出下列四个选项正确的是( )
A. 为奇函数
B. 的最小正周期为
C. 是 的一条对称轴
D. 在 上单调递增
2.已知函数 , , 为 的零点,且 恒成立, 在区间
上有最小值无最大值,则 的取值可以是( )
A.7 B.3 C.5 D.11
3.(多选)已知函数 ,则( )
A. 是周期函数 B. 的图象必有对称轴
C. 的增区间为 D. 的值域为
学科网(北京)股份有限公司1.(2021·全国·高考真题)下列区间中,函数 单调递增的区间是( )
A. B. C. D.
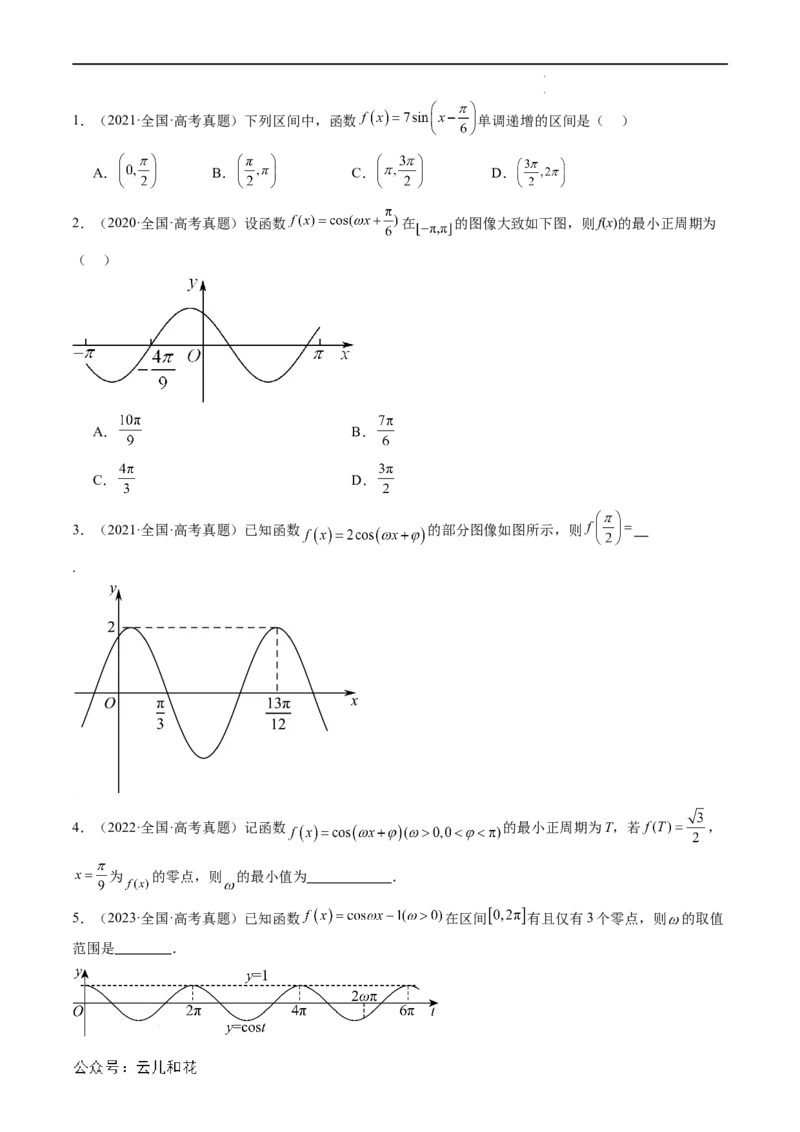
2.(2020·全国·高考真题)设函数 在 的图像大致如下图,则f(x)的最小正周期为
( )
A. B.
C. D.
3.(2021·全国·高考真题)已知函数 的部分图像如图所示,则
.
4.(2022·全国·高考真题)记函数 的最小正周期为T,若 ,
为 的零点,则 的最小值为 .
5.(2023·全国·高考真题)已知函数 在区间 有且仅有3个零点,则 的取值
范围是 .
学科网(北京)股份有限公司学科网(北京)股份有限公司