文档内容
六安二中 2025 届高三第二次月考试题
数学
分值:150分 时间:120分钟
命题人:刘欢审题人:袁绪信
注意事项
1.考生务必将自己的姓名、班级写在答题卡上并粘好条形码.
2.选择题每小题选出答案后,用2B铅笔把答题卡上对应题目的选项涂黑.如需改动,用橡皮擦
干净后,再选涂其它选项.不能答在试题卷上.
3.解答题按照题号在各题的答题区域(黑色线框)内作答,超出答题区域的答案无效.
4.保持答题卡卷面清洁,不折叠,不破损.
第Ⅰ卷(选择题58分)
一、单项选择题:本大题共8小题,每题5分,共40分.在每小题给出的四个选项中,只有一
项是符合题目要求的,请将正确的选项填涂在答题卡上.
1. 设集合 ,集合 ,则 ( )
A. B. C. D.
【答案】C
【解析】
【分析】求解绝对值不等式和函数定义域解得集合 ,再求交集即可.
【详解】根据题意,可得 ,
故 .
故选: .
2. 已知 ,则“ ”是“ ”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
第1页/共21页
学科网(北京)股份有限公司【答案】A
【解析】
【分析】解不等式,进而判断命题的充分必要性.
【详解】解不等式 ,可得 ,
解不等式 ,可得 ,
所以“ ”是“ ”的充分不必要条件,
故选:A.
3. 已知 , , ,则( )
A. B. C. D.
【答案】A
【解析】
【分析】借助特殊角的三角函数值、指数运算和对数函数性质,化简 即可判断大小.
【详解】由题知, , ,
又 ,
所以 .
故选:A
4. 函数 图象大致是( )
的
A. B.
第2页/共21页
学科网(北京)股份有限公司C. D.
【答案】D
【解析】
【分析】确定函数定义域,判断函数奇偶性,即可判断 B;当 时, ,利用导数判断此
时函数的单调性,即可判断A,C,D,即得答案.
【详解】函数函数 的定义域为 ,
设 ,则 ,
故 为偶函数,其图象关于y轴对称,则B中图象错误;
又当 时, , ,
由 ,得 ,由 ,得 ,
故 在 上单调递减,在 上单调递增,
结合选项A,C,D中图象可知只有D中图象符合题意,
故选:D
5. 已知函数 是定义域为 的奇函数,当 时, .若 ,
则m的取值范围为( )
A. B. C. D.
【答案】D
【解析】
【分析】根据函数的对称性作出函数的图象,可知函数为增函数,再利用奇偶性转化不等式为
第3页/共21页
学科网(北京)股份有限公司,再利用单调性求解不等式即可.
【详解】由题意,函数 是定义域为R的奇函数,则 图象关于原点对称.
先作出当 时 的图象,再利用对称性可作出R上的 的图象.
函数 的图象如图.
由图象可知,函数 是R上的增函数.
由 ,得 ,
由 是奇函数,可得 ,
则有 ,
又 是R上增函数,则 ,解得 .
故 的取值范围为(1,+∞).
故选:D.
6. 科学技能的迅猛发展,使人们在学校里学到的专业知识,逐步陈旧过时,这就是所谓的“知识半衰
期”.1950年以前,知识的半衰期为50年:21世纪,知识的半衰期平均为3.2年;IT业高级工程师1.8年.如
果一个高三学生的初始知识量为 ,则经过一定时间,即t个月后的知识量T满足 ,
h称为知识半衰期,其中 是课堂知识量,若 ,某同学知识量从80降至75大约用时1个月,那么
第4页/共21页
学科网(北京)股份有限公司知识量从75降至45大约还需要( )(参考数据:lg2≈0.30,lg11≈1.04)
A. 8个月 B. 9个月 C. 10个月 D. 11个月
【答案】C
【解析】
【分析】根据题意得到方程,求出 ,两边取对数,计算出答案.
【详解】由题意得 ,即 ,
,所以 ,得 ,
两边取对数 , ,
故选:C.
7. 已知函数 ( 且 ),若函数 的值域为 ,则实数a的
取值范围是( )
A. B. C. D.
【答案】B
【解析】
【分析】分析可知当 时, ,由题意可知当 时,则 的值域包含 ,
分 和 两种情况,结合指数函数性质分析求解.
【详解】当 时,则 ,
且 ,所以 ,
第5页/共21页
学科网(北京)股份有限公司若函数 的值域为 ,可知当 时,则 的值域包含 ,
若 ,则 在 内单调递减,
可得 ,不合题意;
若 ,则 在 内单调递增,
可得 ,则 ,解得 ;
综上所述:实数a的取值范围是 .
故选:B.
8. 对于 ,不等式 恒成立,则实数m的取值范围为( )
A. B. C. D.
【答案】C
【解析】
【分析】由 得, ,同构函数 由
得: ,再参变分离,转化为借助导数求函数的最值即可.
【详解】已知 ,由 得, ,
构造函数 则 是R上的增函数,则由 得: ,
即 ,令 , ,
当 则 单调递减,
当 ,则 单调递增,
∴ ,则 又 则 .
第6页/共21页
学科网(北京)股份有限公司故选:C.
二、多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合
题目要求.全部选对的得6分,部分选对的得部分,有选错的得0分.
9. 下列结论中正确的是( )
A. 若函数 的定义域为[0,2],则函数f (2x+2)的定义域为[−1,0]
B. 当 时,不等式 恒成立,则 的取值范围是(0,4)
C. 命题“ ”的否定是“ ”
D. 函数 的值域为
【答案】AD
【解析】
【分析】选项A抽象函数的定义域只需要令变量属于原函数定义域,解出 的范围即可;选项B分类讨论
和 , 时借助二次函数开口方向和 即可解决恒成立问题;选项C是命题的否定,注
意“ ,结论边否定”;选项D讨论自变量的取值范围,从而得到指数函数的值域.
【详解】A:由题设 ,则 ,即f (2x+2)的定义域为[−1,0],正确;
B:当 时,不等式 恒成立,
当 时, 恒成立,
当 时,则需满足 ,则 ,
综上, 的取值范围是 ,不正确,
C:由全称命题的否定为特称命题,故原命题的否定为 ,不正确;
第7页/共21页
学科网(北京)股份有限公司D:令 ,故 ,即 的值域为 ,对.
故选:AD
10. 已知 ,则( )
A. B.
C. D.
【答案】ABD
【解析】
【分析】由题意得 ,且 ,结合基本不等式
以及相关推理逐一验算即可得解.
【详解】则 ,且 ,故D正确;
,A正确;
又由 可知 ,B正确; ,故C错误.
故选:ABD.
11. 设函数 与其导函数 的定义域均为 ,且 为偶函数, ,
则( )
A. B.
C. D.
【答案】BD
【解析】
【分析】由已知条件可得导函数对称性,判断A;由已知推出导函数的对称轴即可判断 B;结合导函数对
第8页/共21页
学科网(北京)股份有限公司称性推出函数周期,进而利用周期进行求值,判断C;根据导数求导法则即可判断D.
【详解】对于A, , ,
即 关于 对称,故A错误;
对于B, 为偶函数,故 ,即 关于 对称,
由 关于 对称,知 ,故B正确;
对于C,因为 ,所以 ,
因为 ,所以 ,
则 ,故 ,则 ,
所以 的周期为4,则 ,故C错误;
对于D,由 ,得 ,
即 ,令 得, ,
故 ,故D正确.
故选:BD.
【点睛】结论点睛:函数的对称性:
(1)若 ,则函数 关于 中心对称;
(2)若 ,则函数 关于 对称.
第Ⅱ卷(非选择题92分)
三、填空题:本题共3小题,每小题5分,共15分.
12. 函数 的单调递减区间为____________
【答案】
第9页/共21页
学科网(北京)股份有限公司【解析】
【分析】先求出函数的定义域,再令 ,然后利用复合函数的单调性求解.\
【详解】函数 的定义域为 ,
令 ,则 ,
因为 是增函数, 在 上是减函数,
所以 单调递减区间为
故答案为:
【点睛】本题主要考查复合函数的单调性,还考查了分析求解问题的能力,属于基础题.
13. 已知曲线 在点 处的切线与曲线 只有一个公共点,则
__________.
【答案】 或
【解析】
【分析】根据导函数与斜率的关系求出切线方程,联立曲线 和切线方程,根据方
程只有一个解求解即可.
【详解】因为 ,所以 ,
所以当 时, ,即切线的斜率为2,
所以由点斜式得 即 ,
联立 整理得 ,
因为切线与曲线 只有一个公共点,
第10页/共21页
学科网(北京)股份有限公司所以方程 只有一个根,
当 时,方程为 只有一个根,满足题意;
当 时, ,即 ,解得 ,
综上 或 ,
故答案为: 或 .
14. 已知函数 若函数 有唯一零点,则实数 的取值范
围是__________.
【答案】 或
【解析】
【分析】 换元后转化为 ,该方程存在唯一解 ,且 ,数形结合求解.
【详解】当 时, 单调递减,图象为以 和 轴为渐近线的双曲线的一支;
当 时,有 ,可得 在 单调递减,在 单调递增
且 , ,画出图象如下:
第11页/共21页
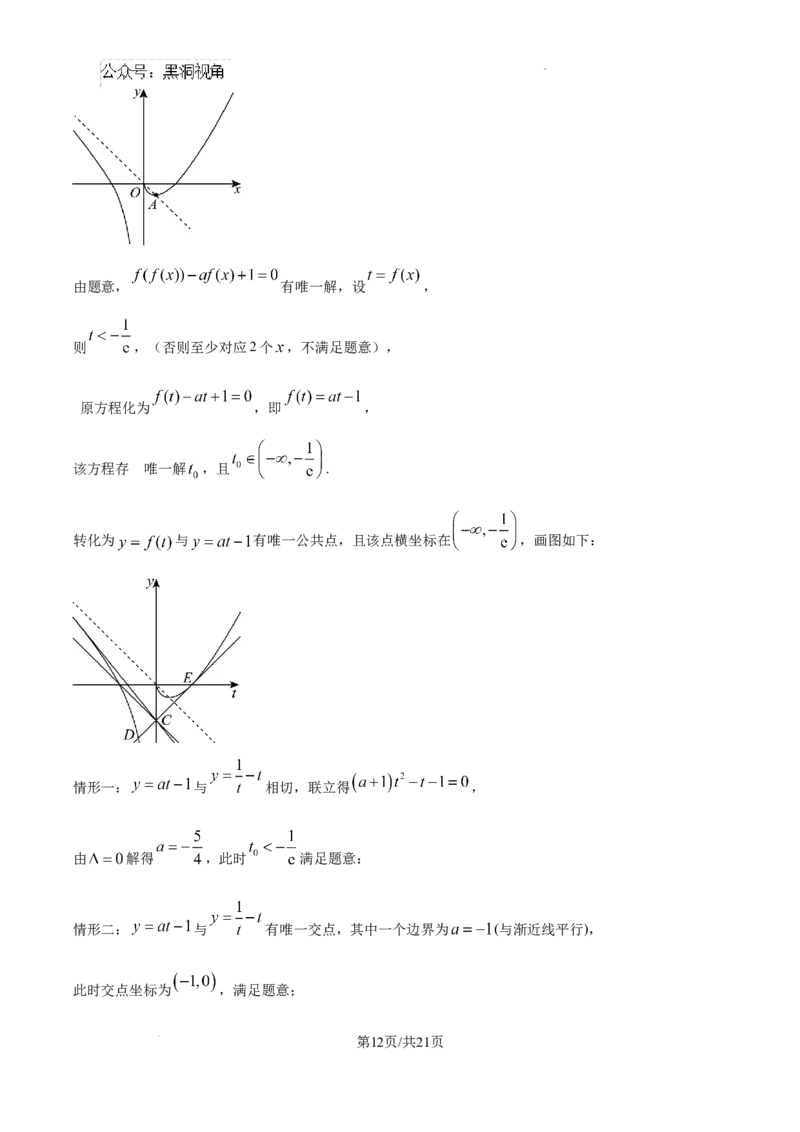
学科网(北京)股份有限公司由题意, 有唯一解,设 ,
则 ,(否则至少对应2个 ,不满足题意),
原方程化为 ,即 ,
该方程存 在唯一解 ,且 .
转化为 与 有唯一公共点,且该点横坐标在 ,画图如下:
情形一: 与 相切,联立得 ,
由 解得 ,此时 满足题意:
情形二: 与 有唯一交点,其中一个边界为 (与渐近线平行),
此时交点坐标为 ,满足题意;
第12页/共21页
学科网(北京)股份有限公司另一个边界为 与 相切,即过点 的切线方程,
设切点为 ,则 ,解得 ,
所以求得 ,此时左侧的交点D横坐标为 满足条件,右侧存在切点E,故该边界无法取到;
所以 的范围为 .
综上, 的取值范围为 或 .
故答案为: 或
【点睛】关键点点睛,解决本题的关键在于第一要换元,令 ,转化为方程 存在唯一
解 ,且 ,作出 与 的图象数形结合求解,第二关键点在于分类讨论后
利用导数或联立方程组求切线的斜率,属于难题.
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15. 已知命题P:“ , ”为假命题,设实数a的所有取值构成的集合为A.
(1)求集合
(2)设集合 ,若 是 的必要不充分条件,求实数m的取值范围.
【答案】(1) 或
(2)
【解析】
【分析】(1)由 :“ , ”为假命题时,可转化为关于 的一元二次方程无解,然后
第13页/共21页
学科网(北京)股份有限公司利用判别式即可;
(2)由 是 的必要不充分条件可得BA,然后分 为空集和非空集两种情况讨论即可.
【小问1详解】
因为命题 为假命题,所以关于 的一元二次方程 无解,
即 ,解得 ,
故集合 ,所以 或 ;
【小问2详解】
由 是 的必要不充分条件,则BA,
当 时, ,解得 ,此时满足BA,
当 时,
则 ,且等号不同时成立,
解得 ,
综上所述, 的取值范围是 .
16. 已知函数 .
(1)判断并证明 的奇偶性;
(2)若对任意 , ,不等式 恒成立,求实数a的取值范围.
【答案】(1)奇函数,证明见解析;
(2) .
第14页/共21页
学科网(北京)股份有限公司【解析】
【分析】(1)利用奇偶性定义证明判断即可;
(2)根据对数复合函数单调性确定 在 上最小值,把问题化为 在
上恒成立,即可求结果.
【小问1详解】
为奇函数,证明如下:
由解析式易知 ,函数定义域为 ,
而 ,故 为奇函数.
【小问2详解】
由 在 上为减函数,而 在定义域上为增函数,
所以 在 上为减函数,故 ,
要使任意 , ,不等式 恒成立,
只需 在 上恒成立,即 在 上恒成立,
由 开口向上,则 ,
综上, .
17. 函数 .
(1)求函数在 处的切线方程;
第15页/共21页
学科网(北京)股份有限公司(2)求出方程 的解的个数.
【答案】(1)
(2)答案见解析
【解析】
【分析】(1)求出函数的导函数,得到切点处切线的斜率,得到切线方程;
(2)作出函数图像,由函数图像与直线 交点个数确定方程解的个数.
【小问1详解】
定义域为: ,
∵
∴
∴切线方程为: .
【小问2详解】
方程解的个数等价于y=f (x)于 的交点个数.
所以 在 上递减,在 上递增,
且 时, ,
作出 与 的图象,
由图可知当 时,方程 的解为0个
当 或 时,方程 的解为1个
当 时,方程 的解为2个
第16页/共21页
学科网(北京)股份有限公司18. 已知函数
的
(1)当 时,求函数 单调区间
(2)若 有两个零点,求 的取值范围
【答案】(1)在 上单调递减;在 上单调递增.
(2)
【解析】
【分析】小问1:先对函数求导,令 ,解得 ,即可求解单调性;
小问2:当 时, ,函数 在 上单调递减,此时函数 最多有一个零点;当
时,由(1)可知: 时,函数 取得极小值,故 ,进而可求出实
数 的取值范围.
【小问1详解】
时, .
令 , ,解得 .
时, , 函数 在 上单调递减;
时, , 函数 在 上单调递增.
第17页/共21页
学科网(北京)股份有限公司【
小问2详解】
.
时, ,函数 在 上单调递减,此时函数 最多有一个零点,不满足题意,舍去.
时,由(1)可知: 时,函数 取得极小值,
有两个零点, ,
令 , (1) .
, 函数 在 上单调递增,
.
又 ; .
满足函数 有两个零点.
的取值范围为 .
19. 从函数的观点看,方程的根就是函数的零点,设函数的零点为 .牛顿在《流数法》一书中,给出了高
次代数方程的一种数值解法——牛顿法.具体做法如下:先在 轴找初始点 ,然后作y=f (x)在点
处切线,切线与 轴交于点 ,再作y=f (x)在点 处切线( 轴,
以下同),切线与 轴交于点. ,再作y=f (x)在点 处切线,一直重复,可得到一列
数: .显然,它们会越来越逼近 .于是,求 近似解的过程转化为求 ,若设精度为 ,则
第18页/共21页
学科网(北京)股份有限公司把首次满足 的 称为 的近似解.
(1)设 ,试用牛顿法求方程 满足精度 的近似解(取 ,且结果
保留小数点后第二位);
(2)如图,设函数 ;
(i)由以前所学知识,我们知道函数 没有零点,你能否用上述材料中的牛顿法加以解释?
(ii)若设初始点为 ,类比上述算法,求所得前 个三角形 的面积
和.
【答案】(1)
(2)(i)答案见解析;(ii)
【解析】
【分析】(1)根据题意分别计算出 ,取 得近似值即为方程 的近似值;
(2)(i)设 ,则 ,由 求得 处的切线方程,
得到 即可;
(ii)再根据 得 ,从而 ,
第19页/共21页
学科网(北京)股份有限公司再结合等比数列的求和公式求解即可;
【小问1详解】
由函数 ,则 ,切线斜率 , ,
那么在 点处的切线方程为 ,
所以 ,且 ,
那么在 点处的切线方程为 ,
所以 ,且 ,
故用牛顿法求方程 满足精度 的近似解为 ;
【小问2详解】
(i)设 ,则 ,
因为 ,所以 ,
则 处切线为 ,
切线与 轴相交得 ,即 为定值,
根据牛顿法,此函数没有零点;
(ii)因为 得 ,
所以 , ,
所以 ,
第20页/共21页
学科网(北京)股份有限公司.
故所得前 个三角形 的面积和为 .
【点睛】关键点点睛:本题第二问的关键在于根据 ,再结合牛顿法得到 .
第21页/共21页
学科网(北京)股份有限公司