文档内容
合肥一中 2025 届高三年级上学期阶段性诊断检测卷
数学试题
(考试时间:120 分钟 满分:150 分)
注意事项:
1. 答题前,务必在答题卡和答题卷规定的地方填写自己的姓名、准考证号和座位号后两位。
2. 答题时, 每小题选出答案后, 用 2B 铅笔把答题卡上对应题目的答案标号涂黑。如需改动, 用
橡皮擦干净后,再选涂其他答案标号。
3. 答题时, 必须使用 0.5 毫米的黑色墨水签字笔在答题卷上书写,要求字体工整、笔迹清晰。作
图题可先用铅笔在答题卷规定的位置绘出, 确认后再用 0.5 毫米的黑色墨水签字笔描清楚。必
须在题号所指示的答题区域作答, 超出答题区域书写的答案无效, 在试题卷、草稿纸上答题无
效。
4. 考试结束, 务必将答题卡和答题卷一并上交。
一、单项选择题: 本题共 8 小题, 每小题 5 分, 共 40 分. 在每小题给出的四个选项中, 只有一项
是符合 题目要求的.
1. 已知集合 A={x∣2x−4>0},B={x∈Z∣1≤x≤5} ,则 A∩B= ( )
A. {2,3,4,5} B. {3,4,5} C. (2,5] D. [2,5]
z
2. =1+i ,则 ´z= ( )
i
A. −1−i B. −1+i C. 1+i D. 1−i
3. 已知 a=(0,1),b=(3,3) ,若满足 c=a+tb ,且 ⃗c⊥⃗b ,则 t= ( )
1 1 1
A. B. − C. − D. 0
6 3 6
7
4. 已知一圆锥高为 2,母线长为 2√2 . 若用一平面截圆锥得到的圆台体积是圆锥的 ,则圆台
8
的侧面积为( )
A. 6√2π B. 4√2π C. 3√2π D. √2π
sinθ+cosθ
5. 已知 tanθ= ,则 tan2θ= ( )
sinθ−cosθ√2
A. 1 B. -1 C. 0 D. −
2
x2 y2
6. 已知实数 x ,x ,y ,y 满足 1− 1 =1,(x −12) 2+ y2=1 ,则 (x −x ) 2+(y −y ) 2 的
1 2 1 2 4 12 2 2 1 2 1 2
最小值为 ( )
A. 96 B. 81 C. 96−8√6 D. 97−8√6
π
7. 已知 0<φ< ,ω>0,f (x)=sin2(ωx+φ)−sin(ωx+φ)cos(ωx+φ) 为偶函数,且
2
g(x)=sin(ωx+φ) 在 [0,2π] 上有 3 个零点,则 ω 的取值范围为 ( )
[23 31) (23 31] [21 29) (21 29]
A. , B. , C. , D. ,
16 16 16 16 16 16 16 16
8. 已知函数 f (x)=ex(ax−1)−x+2 ,若存在唯一的整数 x ,使 f (x )<0 ,则 a 的取值范围
0 0
是 ( )
[1 1 1 1)
A. + , +
4 2e4 3e3 3
B.
( 3e−1,2e2− 1]
2
C. [1 ,1− 1) ∪ ( 3e−1,2e2− 1]
2 e 2
[1 1) [1 1 1 1)
D. ,1− ∪ + , +
2 e 4 2e4 3e3 3
二、多项选择题:本题共 3 小题, 每小题 6 分, 共 18 分, 在每小题给出的四个选项中, 有多项符
合题 目的要求, 全部选对的得 6 分, 部分选对的得部分分, 有选错的得 0 分.
9. 设 A,B,C 是三个随机事件,则下列说法正确的是 ( )
A. 若 A,B 互斥,则 P(A)+P(B)=1
B. 若 A⊆B ,则 P(A)≤P(B)
C. P(A∪B)=P(A)+P(B)−P(AB)
D. 若 A,B 独立,则 P(AB)=[1−P(A)]⋅[1−P(B)]{|x+2|,x≤0
10. 已知函数 f (x)= ,若关于 x 方程 f (x)=t 有四个不同的解 x ,x ,x ,x ,
|log x|,x>0 1 2 3 4
3
1
且 x 1 b>0) 过点 P(2,3) ,焦距为 4,过点
a2 b2
M(−1,0) 斜率为 k 的直线 l 与椭圆 C 交于 A、B 两点,线段 AB 的中点为 N .
(1)求椭圆 C 的标准方程;9
(2)若 △PMN 的面积为 ,求直线 l 的方程.
7
17. (本小题满分 15 分)
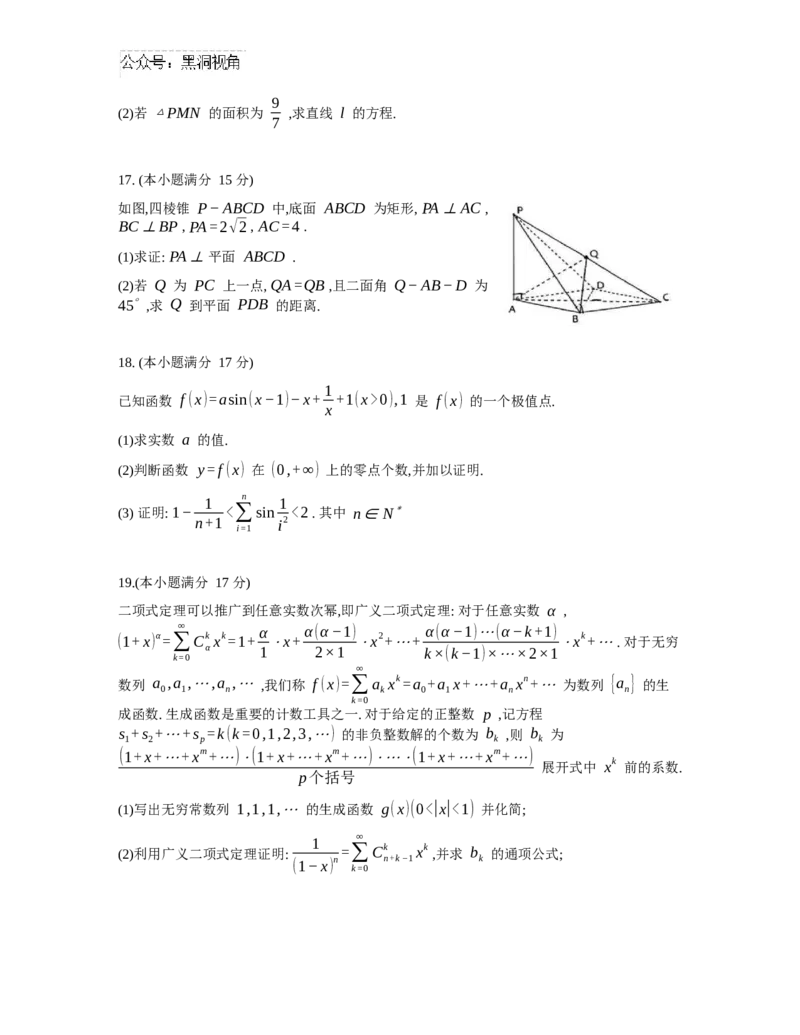
如图,四棱锥 P−ABCD 中,底面 ABCD 为矩形, PA⊥AC ,
BC⊥BP , PA=2√2 , AC=4 .
(1)求证: PA⊥ 平面 ABCD .
(2)若 Q 为 PC 上一点, QA=QB ,且二面角 Q−AB−D 为
45∘ ,求 Q 到平面 PDB 的距离.
18. (本小题满分 17 分)
1
已知函数 f (x)=asin(x−1)−x+ +1(x>0),1 是 f (x) 的一个极值点.
x
(1)求实数 a 的值.
(2)判断函数 y=f (x) 在 (0,+∞) 上的零点个数,并加以证明.
n
1 1
(3) 证明: 1− <∑sin <2 . 其中 n∈N∗
n+1 i2
i=1
19.(本小题满分 17 分)
二项式定理可以推广到任意实数次幂,即广义二项式定理: 对于任意实数 α ,
∞ α α(α−1) α(α−1)⋯(α−k+1)
(1+x) α=∑Ck xk=1+ ⋅x+ ⋅x2+⋯+ ⋅xk+⋯ . 对于无穷
α 1 2×1 k×(k−1)×⋯×2×1
k=0
∞
数列 a ,a ,⋯,a ,⋯ ,我们称 f (x)=∑a xk=a +a x+⋯+a xn+⋯ 为数列 {a } 的生
0 1 n k 0 1 n n
k=0
成函数. 生成函数是重要的计数工具之一. 对于给定的正整数 p ,记方程
s +s +⋯+s =k(k=0,1,2,3,⋯) 的非负整数解的个数为 b ,则 b 为
1 2 p k k
(1+x+⋯+xm+⋯)⋅(1+x+⋯+xm+⋯)⋅⋯⋅(1+x+⋯+xm+⋯)
展开式中 xk 前的系数.
p个括号
(1)写出无穷常数列 1,1,1,⋯ 的生成函数 g(x)(0<|x|<1) 并化简;
∞
1
(2)利用广义二项式定理证明: =∑Ck xk ,并求 b 的通项公式;
(1−x) n
k=0
n+k−1 k(3)一次体质素养测试共分为十一个大项,前十项各有三个小项,第十一项仅有两个小项.运动员需
参加所有项目的测试以获取分数. 计分规则如下:通过第 k(k=1,2,⋯,10) 大项中的每一个小
项,都可获得 2k 分; 通过第十一项中的每一个小项,可获得 1 分.
①记 x ,x ,x 表示第一大项中每一个小项获得的分数, x ,x ,x 表示第二大项中每一个小项
1 2 3 4 5 6
获得的分数, ⋯⋯,x ,x ,x 表示第十大项中每一个小项获得的分数, x ,x 表示第十一大
28 29 30 31 32
项中每一个小项获得的分数. 记 a 为获取 n 分的所有得分组合数. 请写出
n
x (k=1,2,⋯,32) 的取值集合,并用方程解的个数描述 a .
k n
② 求 a .
2025