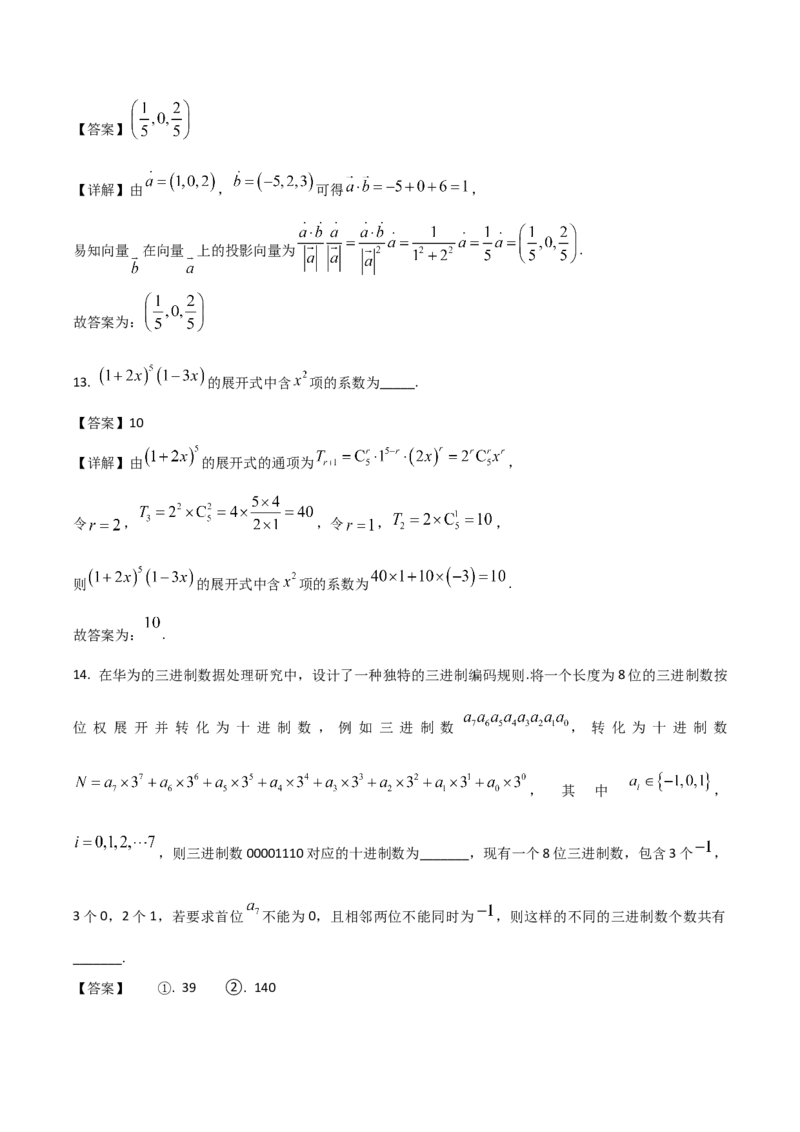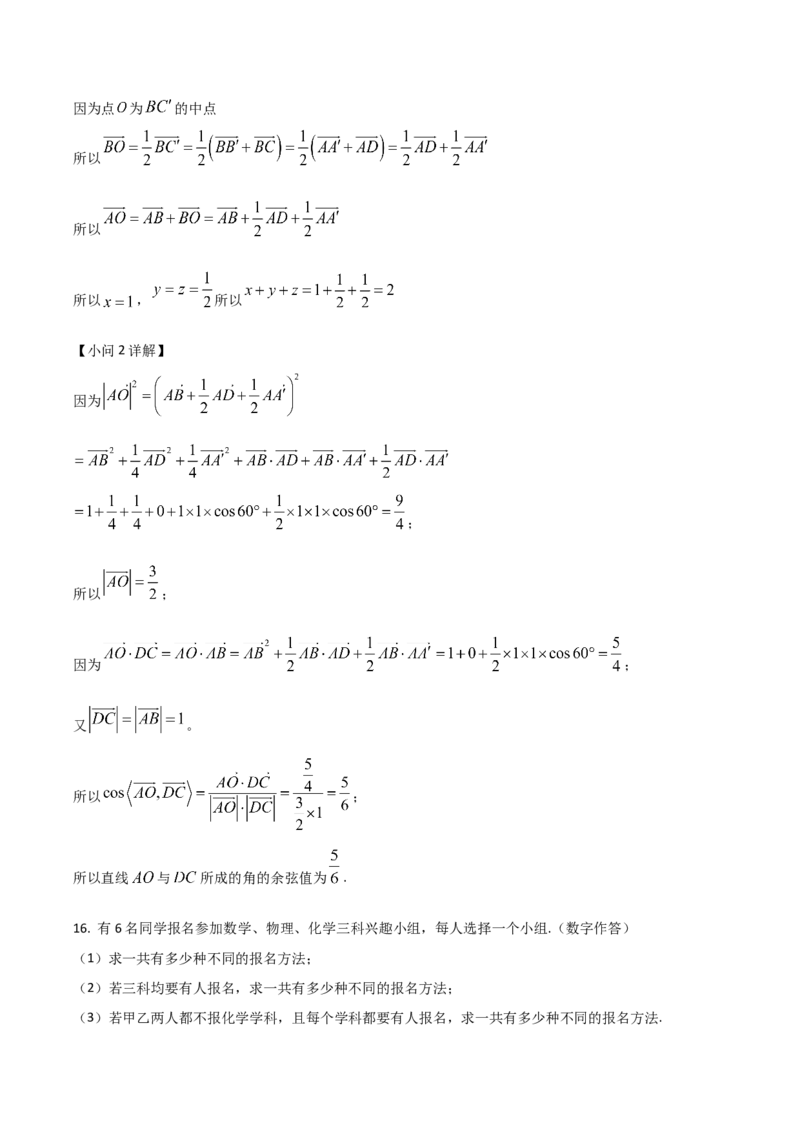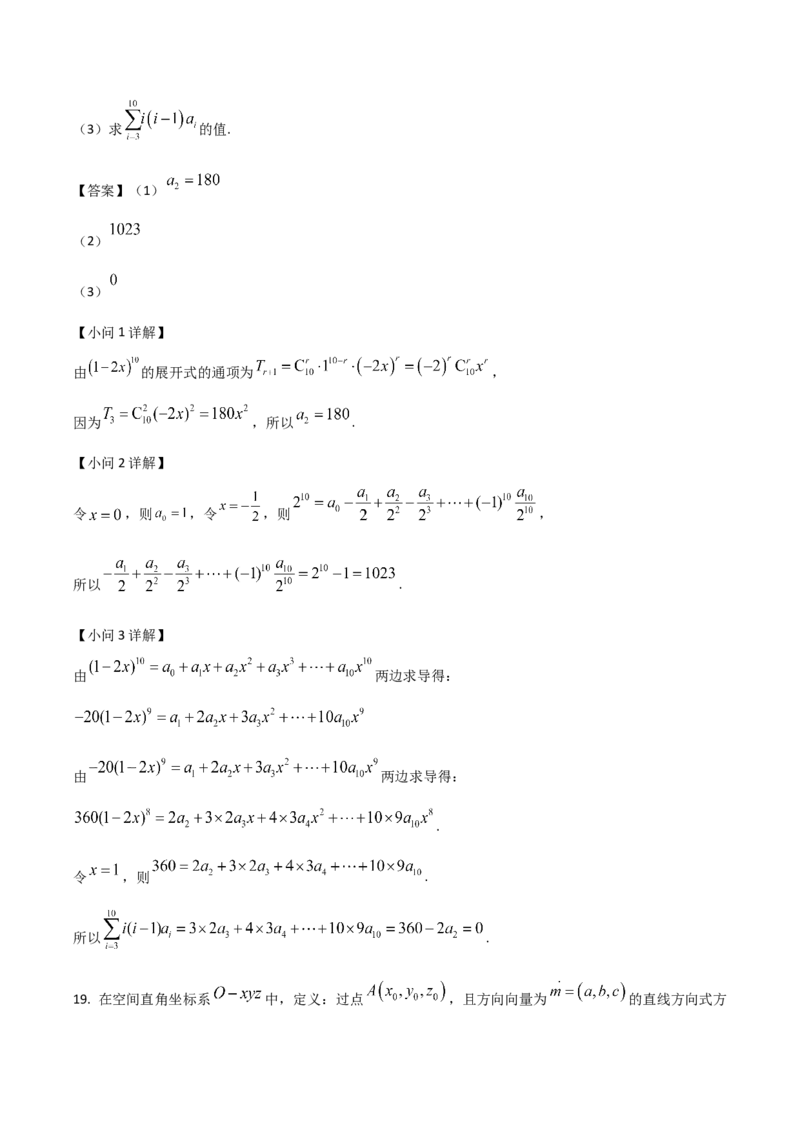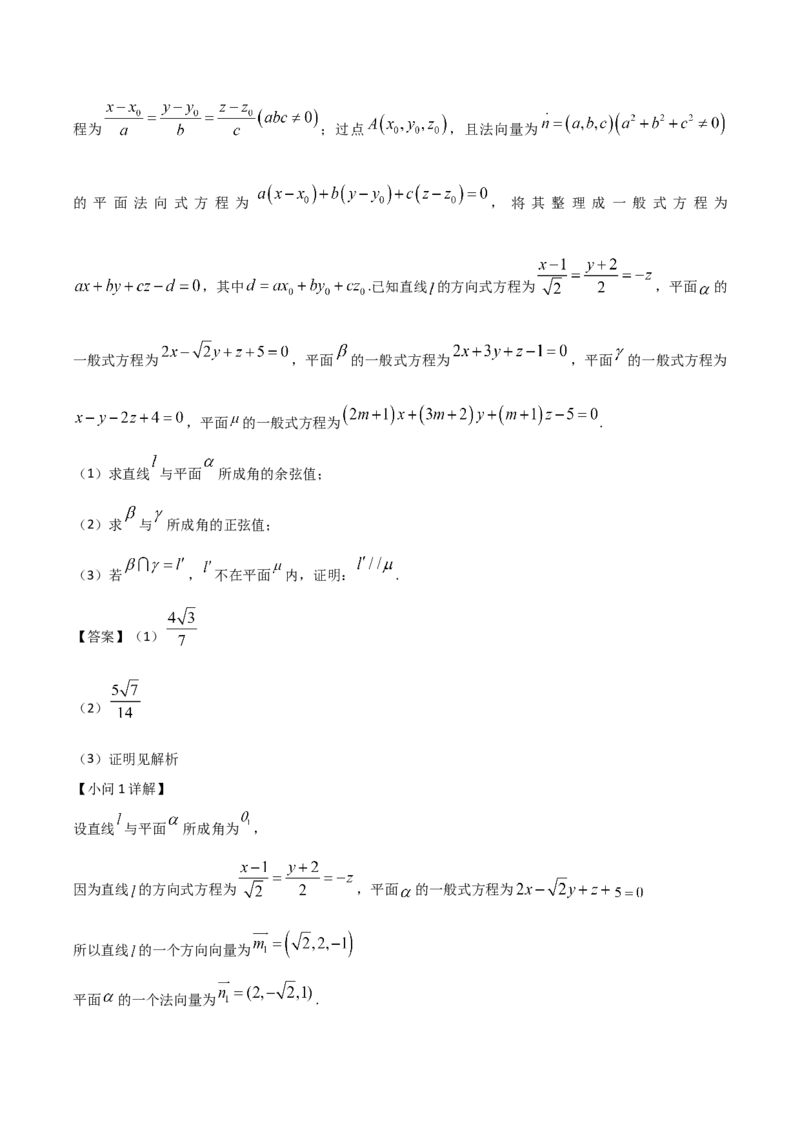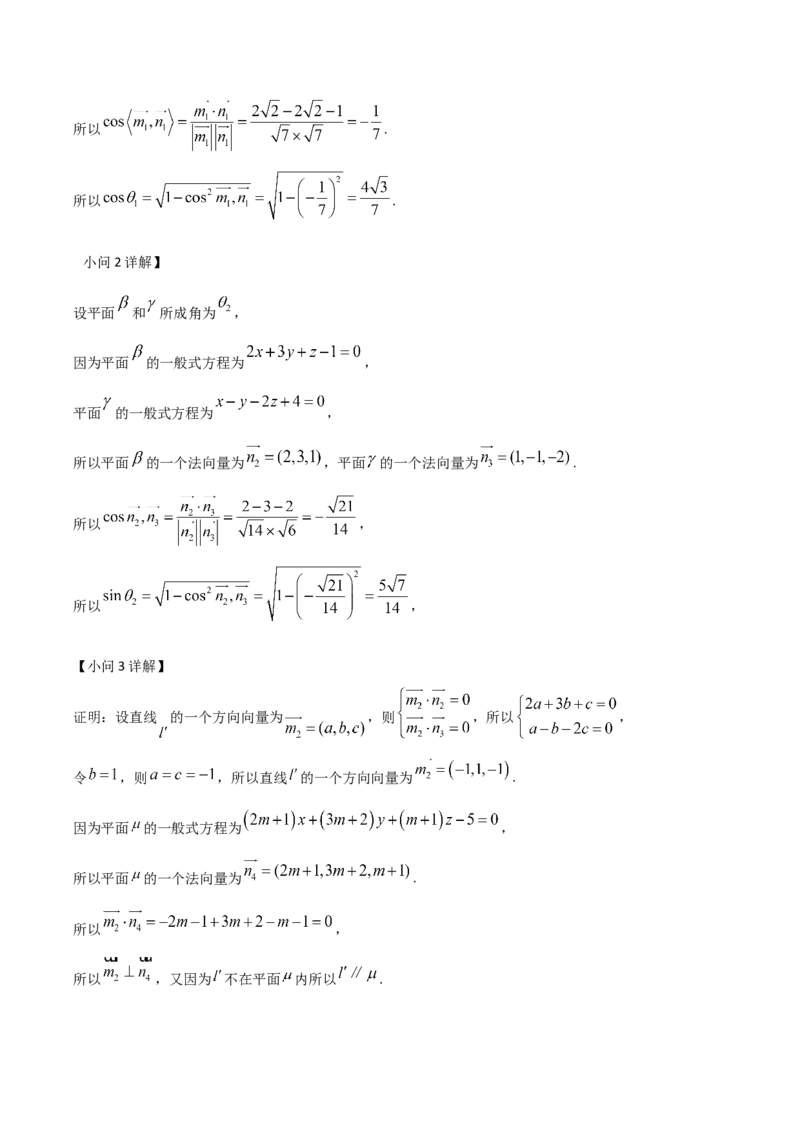文档内容
2024~2025 学年第二学期期中调研试卷
高二数学
(满分150分,考试时间120分钟)
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是
符合题目要求的.
1. 已知 , ,若 ,则x的值为( )
A. 7 B. -8 C. 6 D. -5
【答案】A
【详解】已知 , ,
因为 ,
则 , .
故选:A.
2. 展开式中的第 项为常数项,则 的值为( )
A. 7 B. 8 C. 9 D. 10
【答案】D
【详解】二项式 展开式的通项为 (
且 ),
因为展开式中的第 项为常数项,所以 ,解得 .
故选:D
3. 已知3张卡片的正、反两面分别写有数字1,2;3,4;5,6.将这3张卡片排成一排,则可构成不同的
三位数的个数为( )
A. 120 B. 60 C. 48 D. 36
【答案】C【详解】将3张卡片排成一排,每一张卡片数字有两种情况,则不同的数字组合有 种,
再将3个数字进行排列,则有 种,所以构成的不同三位数有 种.
故选:C
4. 在正三棱柱 中, ,P为 的中点,则直线 与平面 所成角的正弦
值为( )
A. B. C. D.
【答案】A
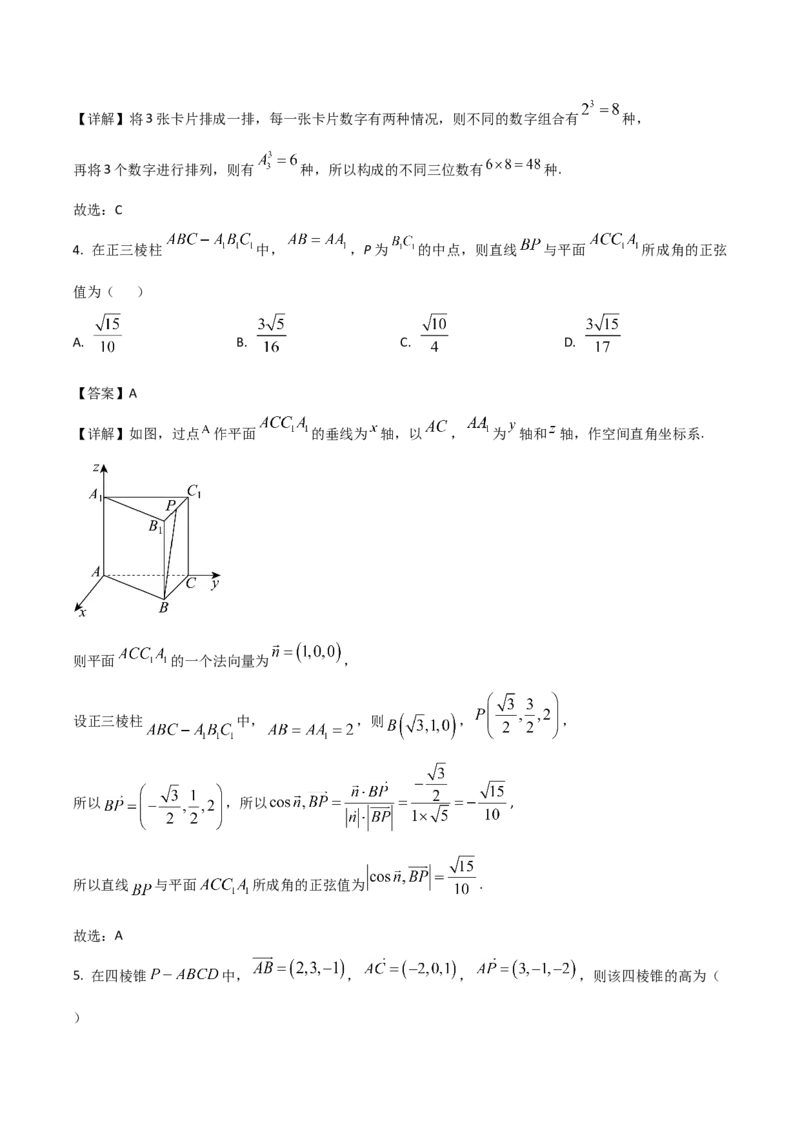
【详解】如图,过点 作平面 的垂线为 轴,以 , 为 轴和 轴,作空间直角坐标系.
则平面 的一个法向量为 ,
设正三棱柱 中, ,则 , ,
所以 ,所以 ,
所以直线 与平面 所成角的正弦值为 .
故选:A
5. 在四棱锥 中, , , ,则该四棱锥的高为(
)A. B. C. D.
【答案】D
【详解】设平面 的一个法向量为 ,
则 ,令 ,可得 , ;
所以 ,
则点 到平面 的距离为 .
故选:D
6. 6名同学排成一排照相,其中甲、乙两人相邻的排法共有( )
A. 120种 B. 240种 C. 360种 D. 480种
【答案】B
【详解】甲和乙两人相邻,有 种方法;将甲、乙两人看成一个元素,和其他四名同学,共5个元素
全排列,有 种方法,
所以甲、乙两人相邻的排法共有 种方法.
故选:B.
7. 若 ,则 ( )
A. 30 B. 45 C. 60 D. 90
【答案】B
【详解】由 ,则其展开式的通项为 ,
令 ,则 .
故选:B.8. 将6封不同的信放入编号为1,2,3,4的4个邮筒,则恰有2个空邮筒的不同的放法共有( )
A. 372种 B. 380种 C. 492种 D. 496种
【答案】A
【详解】首先从 个邮筒中选出 个邮筒,有 种选法,
再将 封不同的信件分成 , , 两组,有 种分法;
最后将两组分配到两个邮筒,有 种分法。
按照分步乘法计数原理可知恰有2个空邮筒的不同的放法共有 种.
故选:A
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目
要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9. 数学竞赛小组有高一学生2人,高二学生4人,高三学生6人,则( )
A. 若每个年级各选1名学生外出培训,则共有12种不同的选法
B. 若选派2名学生外出培训,这2人来自不同年级,则共有44种不同的选法
C. 若选派3名学生外出培训,恰好有1人来自高二年级,则有116种不同的选法
D. 若选派3名学生外出培训,高三年级的甲乙两位同学不能同时参加,则共有210种不同的选法
【答案】BD
【详解】选项A:每个年级各选1名学生外出培训,则共有 种不同的选法,A选项错误;
选项B:若选派2名学生外出培训,这2人来自不同年级,则共有
种不同的选法,故B正确;
选项C:若选派3名学生外出培训,恰好有1人来自高二年级,则有 种不同的选法,
故C错误;
选项D:若选派3名学生外出培训,高三年级的甲乙两位同学不能同时参加,则共有
种情况,故D正确,故选:BD
10. 若 展开式中的常数项为60,则( )
的
A. 展开式中第4项 二项式系数最大 B. 实数a的值为4
C. 展开式中奇数项的二项式系数和为64 D. 展开式中系数最大的项是第5项
【答案】ABD
【详解】A选项,因为 展开式共7项,第4项的二项式系数最大,故A正确;
B选项, ,其中 为整数,且 ,
令 ,解得 ,此时 ,所以 ,B正确;
C选项,展开式中奇数项的二项式系数和为 ,故C错误;
D选项,由 得, ,又 ,所以 ,
且 时, ,系数为正,
所以展开式中系数最大的项为是第5项,故D正确.
故选:ABD.
11. 正方体 中,点P满足 ,若正方体棱长为
1,则下列正确的有( )
A. 若 , ,则 平面
B. 若 ,则三棱锥 的体积为定值
C. 若 ,则点 到直线 的距离的最小值为D. 若 , ,则二面角 的正弦值的最小值为
【答案】ACD
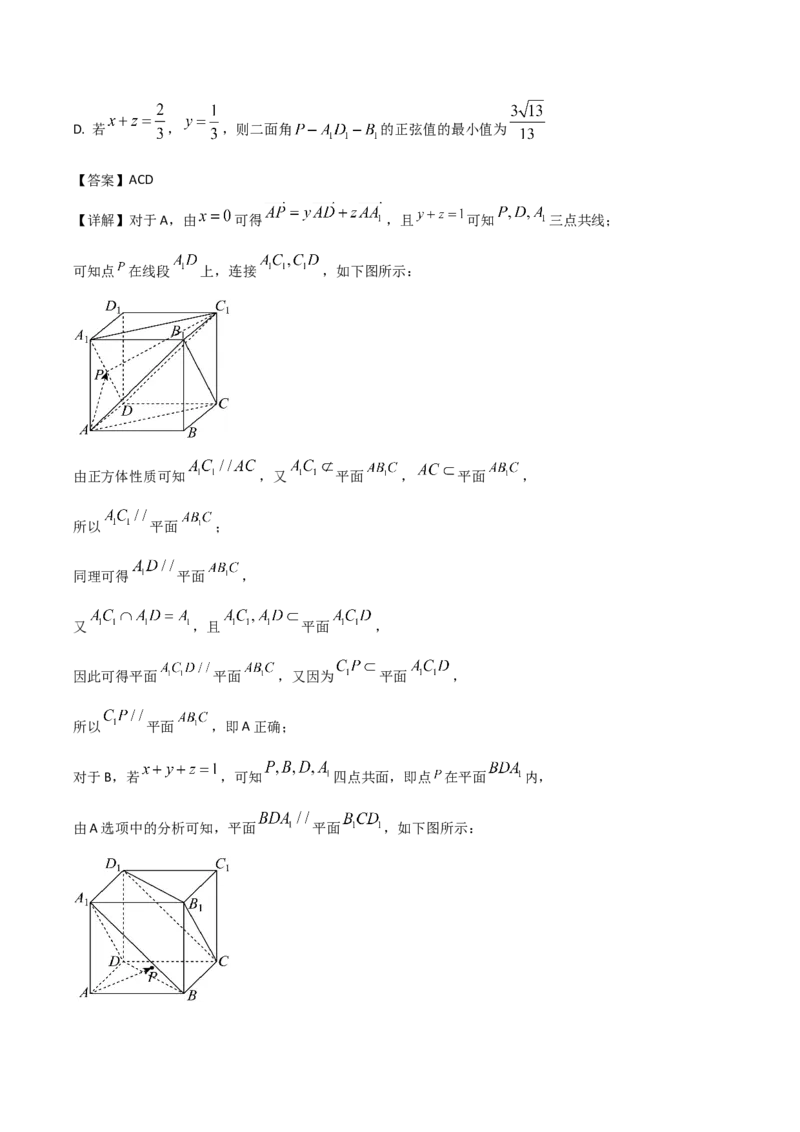
【详解】对于A,由 可得 ,且 可知 三点共线;
可知点 在线段 上,连接 ,如下图所示:
由正方体性质可知 ,又 平面 , 平面 ,
所以 平面 ;
同理可得 平面 ,
又 ,且 平面 ,
因此可得平面 平面 ,又因为 平面 ,
所以 平面 ,即A正确;
对于B,若 ,可知 四点共面,即点 在平面 内,
由A选项中的分析可知,平面 平面 ,如下图所示:此时点 到平面 的距离为正方体对角线的三分之一,即 ;
又三角形 是边长为 的正三角形,其面积为 ,
则三棱锥 的体积为定值 ,即B错误;
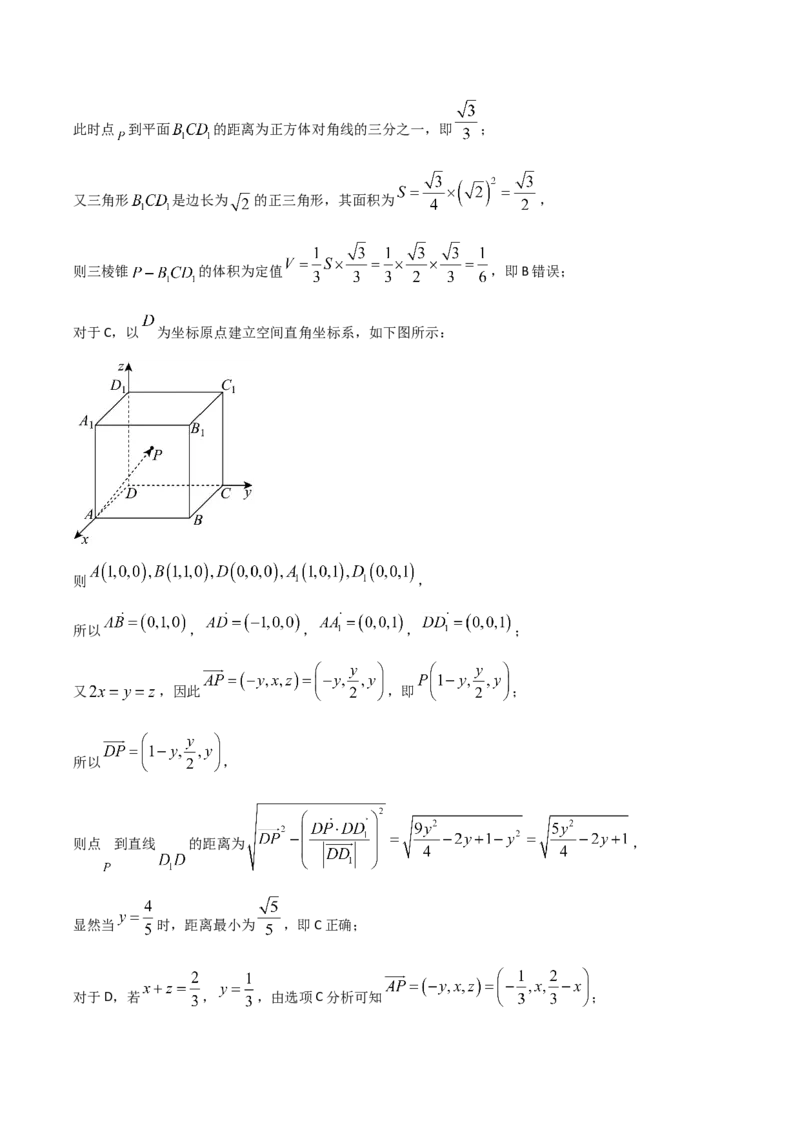
对于C,以 为坐标原点建立空间直角坐标系,如下图所示:
则 ,
所以 , , , ;
又 ,因此 ,即 ;
所以 ,
则点 到直线 的距离为 ,
显然当 时,距离最小为 ,即C正确;
对于D,若 , ,由选项C分析可知 ;则 ,又 ;
设平面 的一个法向量为 ,
则 ,解得 ,令 ,则 ,
因此 ;
易知平面 的一个法向量为 ,
则二面角 的正弦值为 ,
又因为 , ,可知 ,当 时信任不是最小值,
所以 时, ,
易知当 时, ,
即二面角 的正弦值的最小值为 ,可得D正确.
故选:ACD
三、填空题:本题共3小题,每小题5分,共15分.
12. 已知 , ,则向量 在向量 上的投影向量是_________【答案】
【详解】由 , 可得 ,
易知向量 在向量 上的投影向量为 .
故答案为:
13. 的展开式中含 项的系数为_____.
【答案】10
【详解】由 的展开式的通项为 ,
令 , ,令 , ,
则 的展开式中含 项的系数为 .
故答案为: .
14. 在华为的三进制数据处理研究中,设计了一种独特的三进制编码规则.将一个长度为8位的三进制数按
位 权 展 开 并 转 化 为 十 进 制 数 , 例 如 三 进 制 数 , 转 化 为 十 进 制 数
, 其 中 ,
,则三进制数00001110对应的十进制数为_______,现有一个8位三进制数,包含3个 ,
3个0,2个1,若要求首位 不能为0,且相邻两位不能同时为 ,则这样的不同的三进制数个数共有
_______.
【答案】 ①. 39 ②. 140【详解】易知00001110对应的十进制数为 ;
先将3个0,2个1进行排列,共有 种,
再将3个 插入到6个空隙中去,共有 种,
所以能表示出的不同的三进制数个数共有 种,
其中有首位 为0时,共有 种,
则符合题意的不同的三进制数个数共有 种.
故答案为:39;140.
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15. 如 图 , 在 平 行 六 面 体 中 , , ,
,点 为 的中点, .
(1)求 的值;
(2)求 与 所成的角的余弦值.
【答案】(1)
(2)
【小问1详解】因为点 为 的中点
所以
所以
所以 , 所以
【小问2详解】
因为
;
所以 ;
因为 ;
又 。
所以 ;
所以直线 与 所成的角的余弦值为 .
16. 有6名同学报名参加数学、物理、化学三科兴趣小组,每人选择一个小组.(数字作答)
(1)求一共有多少种不同的报名方法;
(2)若三科均要有人报名,求一共有多少种不同的报名方法;
(3)若甲乙两人都不报化学学科,且每个学科都要有人报名,求一共有多少种不同的报名方法.【答案】(1)
(2)540 (3)230
【小问1详解】
因为每个人都有三种选择,所以一共有 种;
【小问2详解】
因为三科均要有人报名,可分为以下三种情况:
①其中一科有4人,另外2科各1人,共有: 种,
②其中一科1人,一科2人,一科3人,共有: 种,
③三科均2人,共有: 种,
所以一共有:90+360+90=540种.
【小问3详解】
因为甲乙两人都不报化学学科,
所以按照另外4个人报化学学科的人数可分为以下4种情况:
①有1人报化学: 种,
②有2人报化学: 种,
③有3人报化学: 种,
④有4人报化学: 种,
所以一共有:120+84+24+2=230种.
17. 如图,在四棱锥 中, 为 的中点, , , , ,
, .(1)求平面 与平面 所成角的正弦值;
(2)在线段 上是否存在点 ,使得 平面 ?若存在,求出点 的位置;若不存在,说明
理由.
【答案】(1)
(2)存在,点 为线段 的中点
【小问1详解】
因为 ,
所以 ,又因为 为 的中点,
所以 与 均为等腰直角三角形,所以
又因为 , 平面 ,
所以 平面 ,又因为 平面 ,
所以 ,又 , 平面 ,所以 平面 ,
在平面 内,过点 作 ,以 为正交基底,建立如图所示的空间直角坐标系
,则 , , , ,
所以 , ,设平面 的一个法向量为
则 ,即 ,令 ,则 ,
平面 的一个法向量为 .
又因为平面 的一个法向量为 ,所以 .
设平面 与平面 所成角为 ,则 .
【小问2详解】
假设线段 上存在点 ,使得 平面
设 ,
所以 .
因为 平面 ,所以 ,
所以 ,即点 是线段 的中点,
所以存在点 ,点 为线段 的中点.
18. 设 .
(1)求实数 的值;
(2)求 的值;(3)求 的值.
【答案】(1)
(2)
(3)
【小问1详解】
由 的展开式的通项为 ,
因为 ,所以 .
【小问2详解】
令 ,则 ,令 ,则 ,
所以 .
【小问3详解】
由 两边求导得:
由 两边求导得:
.
令 ,则 .
所以 .
19. 在空间直角坐标系 中,定义:过点 ,且方向向量为 的直线方向式方程为 ;过点 ,且法向量为
的 平 面 法 向 式 方 程 为 , 将 其 整 理 成 一 般 式 方 程 为
,其中 .已知直线 的方向式方程为 ,平面 的
一般式方程为 ,平面 的一般式方程为 ,平面 的一般式方程为
,平面 的一般式方程为 .
(1)求直线 与平面 所成角的余弦值;
(2)求 与 所成角的正弦值;
(3)若 , 不在平面 内,证明: .
【答案】(1)
(2)
(3)证明见解析
【小问1详解】
设直线 与平面 所成角为 ,
因为直线 的方向式方程为 ,平面 的一般式方程为
所以直线 的一个方向向量为
平面 的一个法向量为 .所以 .
所以 .
【
小问2详解】
设平面 和 所成角为 ,
因为平面 的一般式方程为 ,
平面 的一般式方程为 ,
所以平面 的一个法向量为 ,平面 的一个法向量为 .
所以 ,
所以 ,
【小问3详解】
证明:设直线 的一个方向向量为 ,则 ,所以 ,
令 ,则 ,所以直线 的一个方向向量为 .
因为平面 的一般式方程为 ,
所以平面 的一个法向量为 .
所以 ,
所以 ,又因为 不在平面 内所以 .