辽宁省实验中学2023-2024学年度高考适应性测试（二）数学_2024年3月_02按日期_16号_2024届辽宁省实验中学高考适应性测试（二）

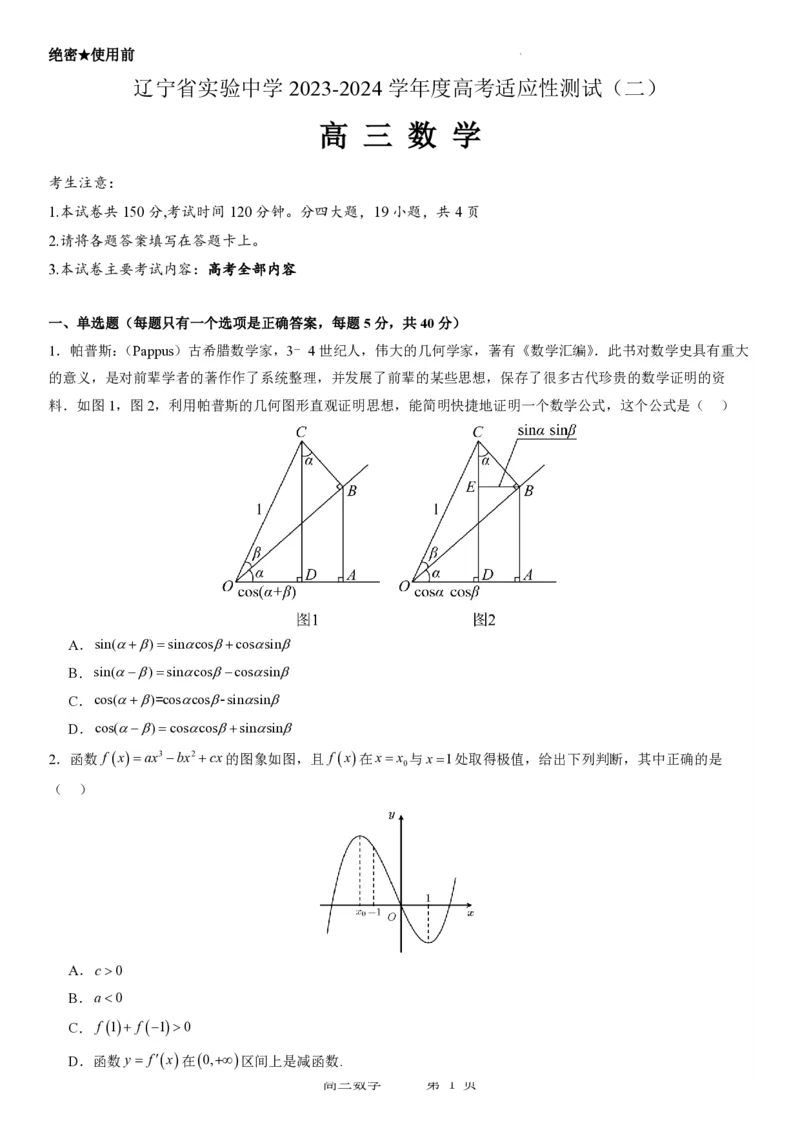
绝密★使用前 辽宁省实验中学 2023-2024 学年度高考适应性测试（二） 高 三 数 学 考生注意： 1.本试卷共150分,考试时间120分钟。分四大题，19小题，共4页 2.请将各题答案填写在答题卡上。 3.本试卷主要考试内容：高考全部内容 一、单选题（每题只有一个选项是正确答案，每题5分，共40分） 1．帕普斯：（Pappus）古希腊数学家，3﹣4世纪人，伟大的几何学家，著有《数学汇编》．此书对数学史具有重大 的意义，是对前辈学者的著作作了系统整理，并发展了前辈的某些思想，保存了很多古代珍贵的数学证明的资 料．如图1，图2，利用帕普斯的几何图形直观证明思想，能简明快捷地证明一个数学公式，这个公式是（ ） A．sin()sincoscossin B．sin()sincoscossin C．cos()=coscos-sinsin D．cos()coscossinsin 2．函数 f xax3bx2cx的图象如图，且 f x在xx 与x1处取得极值，给出下列判断，其中正确的是 0 （ ） A．c0 B．a0 C． f 1 f 10 D．函数y fx在0,区间上是减函数. 高三数学 第 1 页 学科网（北京）股份有限公司3 3．已知双曲线C的离心率为 ，焦点为F,F ，点A在C上，若 FA 2 F A，则cosAF F （ ） 2 1 2 1 2 2 1 1 1 1 1 A． B． C． D． 3 4 5 6 4．将边长为 2的正方形ABCD沿对角线AC折起，使得BD 2，则异面直线AB和CD所成角的余弦值为 （ ） 1 2 3 6 A． B． C． D． 2 2 2 3 4n28n5 5．设数列a 满足a 3,a 3a 4n，若b  ，且数列b 的前n 项和为S ，则S （ ） n 1 n1 n n a a n n n n n1  2  4 2n  1   2  A．n1  B．  C．n1  D．n1   6n9 3 6n9  6n9  6n9 6．若x2x17 a a x2a x22L a x27，则a a a L a （ ） 0 1 2 7 0 1 2 7 A．0 B．1 C．1 D．129 7．已知函数 f xax 2 xlnx有两个零点，则实数a的取值范围是（ ）  1e  1e A．,1 B．0,1 C．,  D．0,   e2   e2  y2 8．过双曲线x2 1的左焦点作直线l交双曲线于A，B两点，若实数使得 AB 的直线l恰有3条，则 2 （ ） A．2 B．3 C．4 D．6 二、多选题（每题至少有一个选项为正确答案，少选且正确得3分，每题6分，共18分） 9．我国南宋数学家杨辉1261年所著的《详解九章算法》一书中展示了二项式系数表，数学爱好者对杨辉三角做 了广泛的研究．则下列结论正确的是（ ） A．第6行、第7行、第8行的第7个数之和为第9行的第8个数 B．1C1 C2C3 C3 5 6 7 8 C．第2020行的第1010个数最大 D．第12行中从左到右第2个数与第3个数之比为2:11 10．如图是数学家Germinal Dandelin用来证明一个平面截圆锥侧面得到的截口曲线是椭圆的模型（称为“Dandelin 双球”）．在圆锥内放两个大小不同的小球，使得它们分别与圆锥的侧面、截面相切，截面分别与球O ，球O 切于 1 2 高三数学 第 2 页 学科网（北京）股份有限公司点E，F（E，F是截口椭圆C的焦点）．设图中球O ，球O 的半径分别为4和1，球心距OO  34，则（ ） 1 2 1 2 A．椭圆C的中心不在直线OO 上 1 2 B． EF 4 5 34 C．直线OO 与椭圆C所在平面所成的角的正弦值为 1 2 34 3 D．椭圆C的离心率为 5 11．英国著名物理学家牛顿用“作切线”的方法求函数零点.已知二次函数 f(x)有两个不相等的实根b,c，其中cb. 在函数 f(x)图象上横坐标为x的点处作曲线y f(x)的切线，切线与x轴交点的横坐标为x；用x代替x，重复 1 2 2 1 x b 以上的过程得到x ；一直下去，得到数列{x }.记a ln n ，且a 1，x c，下列说法正确的是（ ） 3 n n x c 1 n n ecb A．x  （其中lne1） B．数列{a }是递减数列 1 e1 n 1  1  C．a  D．数列a  的前n项和S 2n21n1 6 32  n a  n n 三、填空题（每题5分，共15分） 12．方程3sinx1cos2x在区间0,2上的所有解的和为 . 13．古希腊数学家阿波罗尼斯在《圆锥曲线论》中记载了用平面截圆锥得到圆锥曲线的方法，如图，将两个完全 相同的圆锥对顶放置（两圆锥的顶点和轴都重合），已知两个圆锥的底面直径均为2，侧面积均为 5π，记过两个 圆锥轴的截面为平面，平面与两个圆锥侧面的交线为AC、BD．已知平面平行于平面，平面与两个圆 锥侧面的交线为双曲线C的一部分，且C的两条渐近线分别平行于AC、BD，则该双曲线C的离心率 为 ． 14．我国古代名著《庄子•天下篇》中有一句名言“一尺之棰，日取其半，万世不竭”，其意思为：一尺的木棍，每 天截取一半，永远都截不完.已知长度为2 3的线段PQ，取PQ的中点M ，以PM 为边作等边三角形（如图1）， 1 1 该等边三角形的面积为S ，再取M Q的中点M ，以M M 为边作等边三角形（如图2），图2中所有的等边三角 1 1 2 1 2 n 1 形的面积之和为S ，以此类推，则S  ，  . 2 3 4k1S S k1 k k1 高三数学 第 3 页 学科网（北京）股份有限公司四、解答题 1 15．已知函数 f(x)sin2x 3sinxcosx (0)． 2  π (1)当1时，求函数 f(x)在0, 上的值域；  2 (2)在VABC中，内角A,B,C的对边分别为a,b,c,AD为BAC的平分线，若 f(x)的最小正周期是  A 2 3 2π, f  0,a 3,AD ，求VABC的面积．  2 3 16．已知正项数列a 的前n项和为S ，且满足8S a 24a 4. n n n n n (1)求数列a 的通项公式； n 2n1n为奇数  (2)若b 1 ，{b }的前n项和为T ，求T . n  a n为偶数 n n 2n 2 n1 17．已知函数 f xxlnxalnxa． (1)若a1，当x1时，证明： f x0． (2)若a2，证明： f x恰有一个零点． 7 x2 y2 x2 y2 18．已知离心率为 的双曲线C ：  1a0,b0过椭圆C ：  1的左，右顶点A，B. 2 1 a2 b2 2 4 3 (1)求双曲线C 的方程； 1 (2)Px ,y x 0,y 0是双曲线C 上一点，直线AP，BP与椭圆C 分别交于D，E，设直线DE与x轴交于 0 0 0 0 1 2 Q  x ,0  ，且x 2x  0 1 ，记△BDP与△ABD的外接圆的面积分别为S ，S ，求 S 1 的取值范围. Q Q 0  2 1 2 S 2 19．同余定理是数论中的重要内容．同余的定义为：设a,bZ,mN 且m 1．若m∣(ab)，则称a与b关于模  m同余，记作ab(modm)（“|”为整除符号）． (1)解同余方程：x22x0(mod3)； (2)设（1）中方程的所有正根构成数列a ，其中a a a L a ． n 1 2 3 n 高三数学 第 4 页 学科网（北京）股份有限公司①若b a a nN ，数列b 的前n项和为S ，求S ； n n1 n + n n 4048 ②若C tana tana nN ，求数列C 的前n项和T ． n 2n3 2n1  n n 高三数学 第 5 页 学科网（北京）股份有限公司