文档内容
高二数学试卷
注意事项:
1.答题前,考生务必将自己的姓名、考生号、考场号、座位号填写在答题卡上.
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动.
用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上
无效.
3.考试结束后.将本试卷和答题卡一并交回.
4.本试卷主要考试内容:北师大版选择性必修第一册.
一、选择题:本题共 8 小题,每小题 5 分,共 40 分.在每小题给出的四个选项中,只有一项是
符合题目要求的.
1. 某书架的第一层放有 7 本不同的历史书,第二层放有 6 本不同的地理书.从这些书中任取 1 本历史书和 1
本地理书,不同的取法有( )
A. 13 种 B. 42 种 C. 种 D. 种
【答案】B
【解析】
【分析】根据分步乘法计数原理求解即可.
【详解】7 本不同的历史书任取 1 本历史书有 7 种取法;
6 本不同的地理书任取 1 本地理书有 6 种取法,
从这些书中任取 1 本历史书和 1 本地理书,
根据分步乘法原理得到不同的取法有 7×6=42 种.
故选:B.
2. 已知直线 与直线 平行,则 ( )
A. 1 B. 3 C. 1 或 D. 或 3
【答案】C
【解析】
【分析】根据一般式方程两直线平行的条件得到方程,求出参数的值,再检验即可.
【详解】因为直线 与直线 平行,
所以 ,解得 或 ,
第 1页/共 18页
学科网(北京)股份有限公司经检验,当 或 时,均满足两条直线平行.
故选:C
3. 若直线 与圆 只有一个公共点,则 ( )
A. B. 1 C. 0 D. 2
【答案】C
【解析】
【分析】根据给定条件,可得直线 与圆 相切,再借助点到直线距离公式计算即得.
【详解】依题意,直线 与圆 相切,而圆 的圆心 ,半径为 1,
因此 ,解得 ,
所以 .
故选:C
4. 某农业科学院培育脐橙新品种,新培育的脐橙单果质量 (单位:g)近似服从正态分布 ,
现有该新品种脐橙 10000 个,估计单果质量不低于 150g 的脐橙个数为( )
附:若 ,则 , ,
.
A. 8413 B. 9772 C. 9974 D. 9987
【答案】D
【解析】
【分析】由条件求出 和 值,依据正态分布的对称性可得质量不低于 150g 的概率,即可得解.
【详解】由 可知, , ,
则 ,
故单果质量不低于 150g 的脐橙个数约为 10000×0.9987=9987.
故选:D
5. 小花准备将一颗黄色圣女果、一颗红色圣女果、一颗山楂、一颗草莓、一颗葡萄串起来制作一串冰糖葫
芦,若要求两颗圣女果不相邻,则不同的串法有( )
A. 种 B. 种 C. 种 D. 种
第 2页/共 18页
学科网(北京)股份有限公司【答案】C
【解析】
【分析】利用插空法可求得结果.
【详解】先将一颗山楂、一颗草莓、一颗葡萄进行排序,
然后将两颗圣女果插入一颗山楂、一颗草莓、一颗葡萄所形成的空位中,
从 个空位中抽取 个空位进行排序,
由插空法可知,不同的串法有 种.
故选:C.
6. 已知 为坐标原点,双曲线 的右焦点为 F,点 在 C 的渐近线上,过点
F 作 ,垂足为 , ,则 C 的方程为( )
A. B.
C. D.
【答案】A
【解析】
【分析】由两点距离公式及向量运算得 ,根据点线距离求出 ,由点 在 C 的渐
近线上得 ,.
【详解】由 知 ,又 ,所以 .
由 ,则 为焦点 F 到渐近线 即 的距离,
所以 ,在 中, ,
由点 在 C 的渐近线上,所以 ,即 ,所以 ,
第 3页/共 18页
学科网(北京)股份有限公司所以 C 的方程为 .
故选:A
7. 小明参加户外植树活动,种植了 A,B 两种树苗各 5 棵,A 种树苗的成活率为 0.8,B 种树苗的成活率为
0.6,记 A,B 两种树苗最终成活的棵数分别为 , ,则 ( )
注:设 X,Y 两个随机变量,则有 .
A. 5 B. 6 C. 7 D. 8
【答案】C
【解析】
【分析】根据二项分布的期望性质直接计算即可.
【详解】 服从二项分布 , .
同理, ,
.
故选:C.
8. 在 四 棱 锥 中 , 底 面 是 菱 形 , , , E 是 上 一 点 ,
且
, , , ,则 ( )
A. B. C. D. 2
【答案】B
【解析】
【分析】根据空间向量的线性运算可得 ,再结合数量积运算求解即可.
【详解】因为 ,则 ,
又因为 , , ,则 ,
且 , ,则 ,
可得 ,
则
第 4页/共 18页
学科网(北京)股份有限公司,
所以 ,即 .
故选:B.
二、选择题:本题共 3 小题,每小题 6 分,共 18 分.在每小题给出的选项中,有多项符合题目
要求.全部选对的得 6 分,部分选对的得分分,有选错的得 0 分.
9. 由一组样本数据 ,利用最小二乘法得到两个变量的回归直线方程为
,记 , ,则下面说法正确的是( )
A. 直线 至少经过点 中的一个点
B. 直线 必经过点
C. 样本相关系数 与回归系数 同号
D. 对样本相关系数 , 越大,两个变量之间的线性相关性越强
【答案】BCD
【解析】
【分析】根据回归直线性质、相关系数、回归系数的概念逐项分析可得答案.
【详解】回归直线是由点拟合而成的,可能不过任何一个样本点,但必过数据的中心点,A 错误,B 正确.
样本相关系数 为正时,两个变量为正相关,回归系数 为正;样本相关系数 为负时,
两个变量为负相关,回归系数 为负.故样本相关系数 与回归系数 同号,C 正确.
样本相关系数 , 越大,两个变量之间的线性相关性越强,D 正确.
故选:BCD.
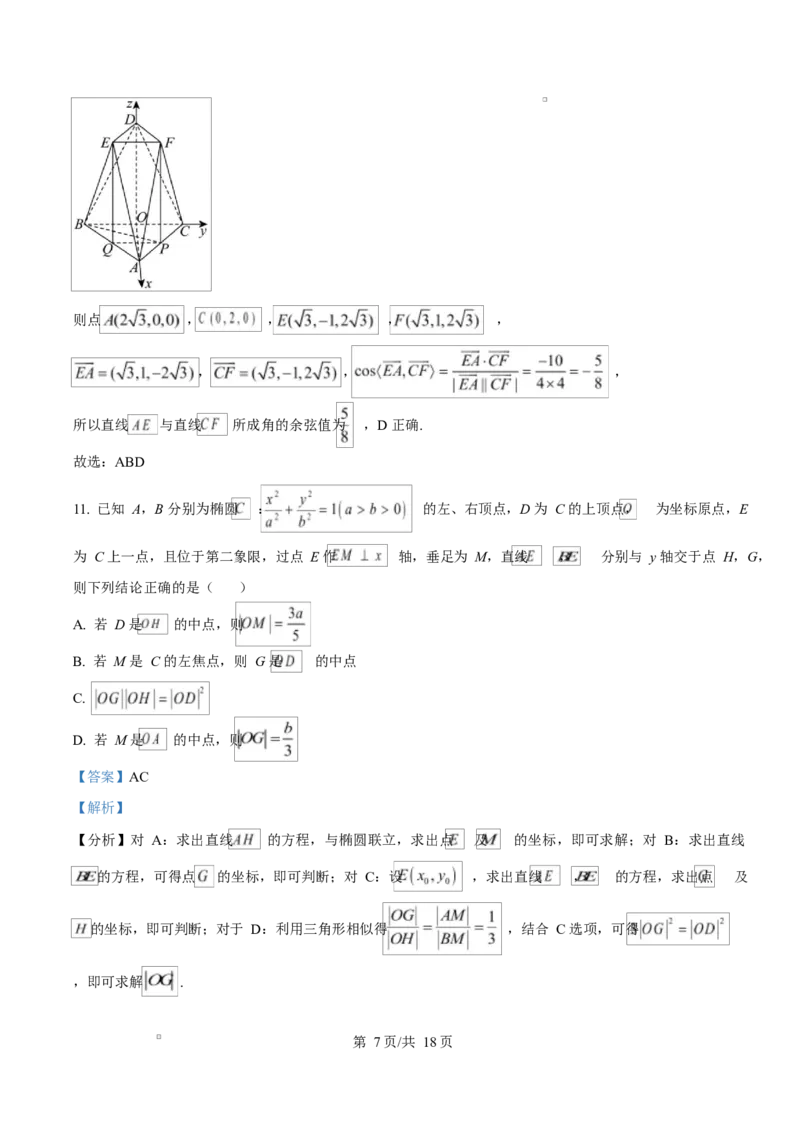
10. 如图,在八面体 中, , , , 均是边长为 4 的正三角形,且
平面 , , 均垂直于底面 ,下列结论正确的是( )
第 5页/共 18页
学科网(北京)股份有限公司A. B. 为正三角形
C. 点 到平面 的距离为 2 D. 直线 与直线 所成角的余弦值为
【答案】ABD
【解析】
【分析】利用面面垂直的性质、线面垂直的性质推理判断 A;证明 、 ,
判断 B;利用线面平行的性质求出点 到平面 的距离判断 C;建立空间直角坐标系,利
用空间向量求出线面角的余弦判断 D.
【详解】取 的中点 ,连接 ,
在正 ,正 中, ,
由平面 平面 ,平面 平面 , 平面 ,则 平面 ,
同理 平面 ,于是 ,四边形 为平行四边形, , ,
而 , ,因此 , ,A 正确;
同理 , ,则 ,即 为正三角形,B 正确;
由 , 平面 , 平面 ,得 平面 ,
则点 到平面 的距离等于点 到平面 的距离,
连接 , 是 的中点,则点 到平面 的距离是点 到平面 的距离的一半,
而点 到平面 的距离为 ,因此点 到平面 的距离为 ,C 错误;
记 的中点为 ,以 为坐标原点,建立如图所示的空间直角坐标系,
第 6页/共 18页
学科网(北京)股份有限公司则点 , , , ,
, , ,
所以直线 与直线 所成角的余弦值为 ,D 正确.
故选:ABD
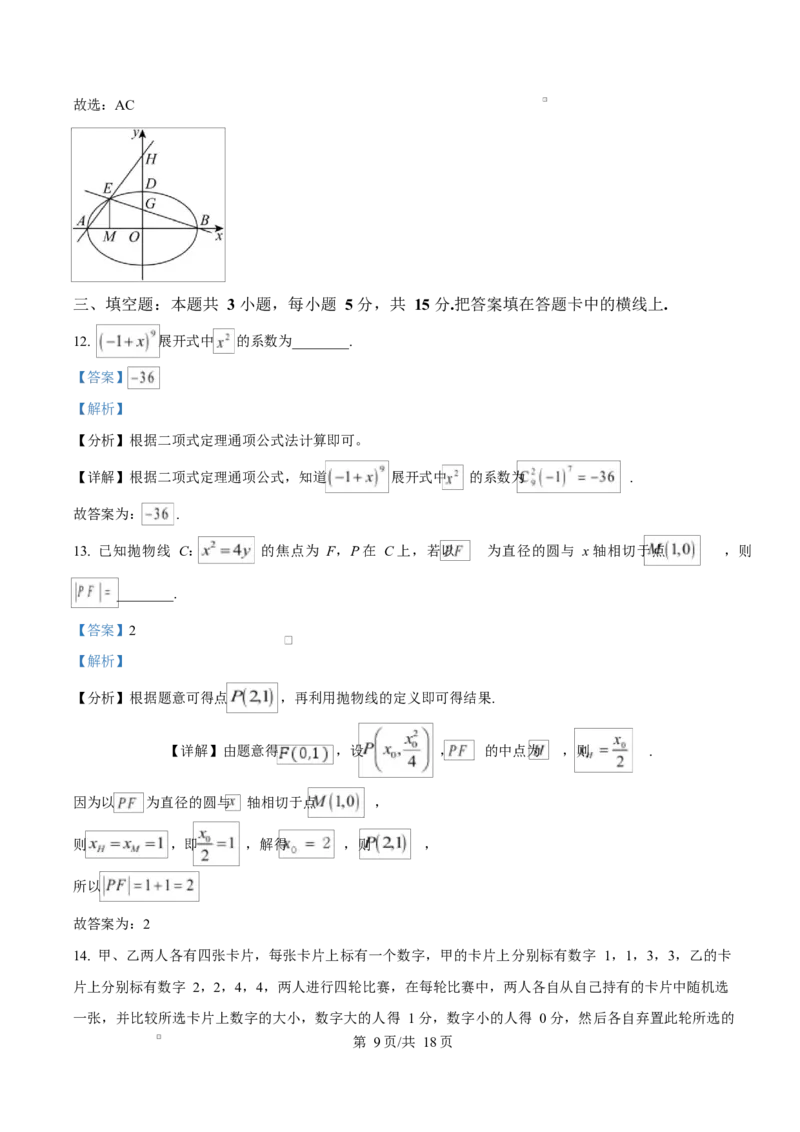
11. 已知 A,B 分别为椭圆 : 的左、右顶点,D 为 C 的上顶点, 为坐标原点,E
为 C 上一点,且位于第二象限,过点 E 作 轴,垂足为 M,直线 , 分别与 y 轴交于点 H,G,
则下列结论正确的是( )
A. 若 D 是 的中点,则
B. 若 M 是 C 的左焦点,则 G 是 的中点
C.
D. 若 M 是 的中点,则
【答案】AC
【解析】
【分析】对 A:求出直线 的方程,与椭圆联立,求出点 及 的坐标,即可求解;对 B:求出直线
的方程,可得点 的坐标,即可判断;对 C:设 ,求出直线 , 的方程,求出点 及
的坐标,即可判断;对于 D:利用三角形相似得 ,结合 C 选项,可得
,即可求解 .
第 7页/共 18页
学科网(北京)股份有限公司【详解】由 是 的中点,则 ,又 ,则直线 的方程为 ,
与 联立可得 ,解得 或 ,
将 代入 ,可得, ,
即 ,则 ,故 ,A 正确.
若 是 的左焦点,则 ,直线 的方程为 .
令 ,得 ,所以 .令 ,得 ,
即当 时, 是 的中点,B 错误.
设 ,直线 , 的斜率分别为 , ,
则 , , .
直线 , 的方程分别为 , ,
分别令 ,可得 , ,所以 , .
,C 正确.
由 ∽ 得 ,由 ∽ 得 ,
可得 .
因为 是 的中点,所以 .
结合 ,可得 ,
所以 ,D 错误.
第 8页/共 18页
学科网(北京)股份有限公司故选:AC
三、填空题:本题共 3 小题,每小题 5 分,共 15 分.把答案填在答题卡中的横线上.
12. 展开式中 的系数为________.
【答案】
【解析】
【分析】根据二项式定理通项公式法计算即可。
【详解】根据二项式定理通项公式,知道 展开式中 的系数为 .
故答案为: .
13. 已知抛物线 C: 的焦点为 F,P 在 C 上,若以 为直径的圆与 x 轴相切于点 ,则
________.
【答案】2
【解析】
【分析】根据题意可得点 ,再利用抛物线的定义即可得结果.
【详解】由题意得 ,设 , 的中点为 ,则 .
因为以 为直径的圆与 轴相切于点 ,
则 ,即 ,解得 ,则 ,
所以
故答案为:2
14. 甲、乙两人各有四张卡片,每张卡片上标有一个数字,甲的卡片上分别标有数字 1,1,3,3,乙的卡
片上分别标有数字 2,2,4,4,两人进行四轮比赛,在每轮比赛中,两人各自从自己持有的卡片中随机选
一张,并比较所选卡片上数字的大小,数字大的人得 1 分,数字小的人得 0 分,然后各自弃置此轮所选的
第 9页/共 18页
学科网(北京)股份有限公司卡片(弃置的卡片在此后的轮次中不能使用),则甲在第一轮比赛中得 1 分的概率为_________,甲的总得
分为 1 的概率为_________.
【答案】 ①. ②.
【解析】
【分析】①设“甲在第一轮比赛中得 1 分”为事件 ,求得 , ,利用古典概型的概率公式运算
即可.②甲的总得分可能为 0,1,2,分别求甲的总得分为 0,2 的概率,即得“甲的总得分为 1 的概率”.
【详解】设样本空间为 ,甲在第一轮比赛中得 1 分为事件 A,
在第一轮比赛中,甲、乙两人所选卡片上的数字可能为(1,2),(1,4),(3,2),(3,4),即
只有一种情况(3,2)满足甲在第一轮比赛中得 1 分,即 ,
所以甲在第一轮比赛中得 1 分的概率为 .
甲的总得分可能为 0,1,2.由于对称性,不妨固定乙四轮所选卡片上的数字依次为(2,2,4,4),甲四轮
所选卡片上的数字有 种排序方法.
若甲的总得分为 0,则甲四轮所选卡片上的数字依次为(1,1,3,3);
若甲的总得分为 2,则甲四轮所选卡片上的数字依次为(3,3,1,1).
故甲的总得分为 0,2 的概率均为 ,甲的总得分为 1 的概率为 .
故答案为: ; .
四、解答题:本题共 5 小题,共 77 分.解答应写出文字说明、证明过程或演算步骤.
15. 袋中装有 12 个大小相同的球,其中红球 2 个,黄球 3 个,白球 7 个,从中随机取出 3 个球.
(1)求取出的 3 个球中有 2 个白球的概率;
(2)设 X 表示取到的红球个数,求 X 的分布列与数学期望.
【答案】(1)
(2)分布列见解析,
【解析】
【分析】(1)应用超几何分布的概率公式求概率即可.
(2)先分别应用超几何分布的概率公式求出对应概率,再写出分布列,再求数学期望即可.
【小问 1 详解】
第 10页/共 18页
学科网(北京)股份有限公司所求概率为
【小问 2 详解】
X 可能的取值为 0,1,2.
,
.
故 X 的分布列为
0 1 2
故 .
16. 为了研究某中药预防方对预防某种疾病的效果,科学家进行了实验,得到如下结果(单位:人):
患病情况 患 不 患
服用情况 病 病
服用中药预防方 10 90
不 服 用 中 药 预 防
50 50
方
(1)该中药预防方对预防该种疾病是否有效?
(2)从参与该实验的人中任选一人,A 表示事件“选到的人服用中药预防方”,B 表示事件“选到的人患病”.
利用该调查数据,求 , 的值.
附: ,其中 .
第 11页/共 18页
学科网(北京)股份有限公司0.10 0.05 0.01
2.706 3.841 6.635
【答案】(1)有 99%的把握认为该中药预防方对预防该种疾病有效
(2) , .
【解析】
【分析】(1)利用 的性质进行比较.
(2)利用条件概率,分析情况得到答案.
小问 1 详解】
由已知得 ,
所以有 99%的把握认为该中药预防方对预防该种疾病有效.
【小问 2 详解】
由题意可得 , ,
, .
,
17. 如图,在三棱锥 中, 是边长为 2 的正三角形, 平面 , ,点 为
上的动点.
(1)求三棱锥 的体积;
(2)当 最小时,求平面 与平面 所成角的余弦值.
第 12页/共 18页
学科网(北京)股份有限公司【答案】(1)
(2)
【解析】
【分析】(1)求出底面积和高,根据棱锥体积公式计算即可;
(2)建立空间直角坐标系,求出关键点坐标,借助二次函数性质,求得所以当 时, 有最小值.再
求出面的法向量,借助向量夹角余弦值公式计算即可.
【小问 1 详解】
容易求得 .
因为 平面 ,所以 是三棱锥 的高.
中, ,
所以三棱锥 的体积 .
【小问 2 详解】
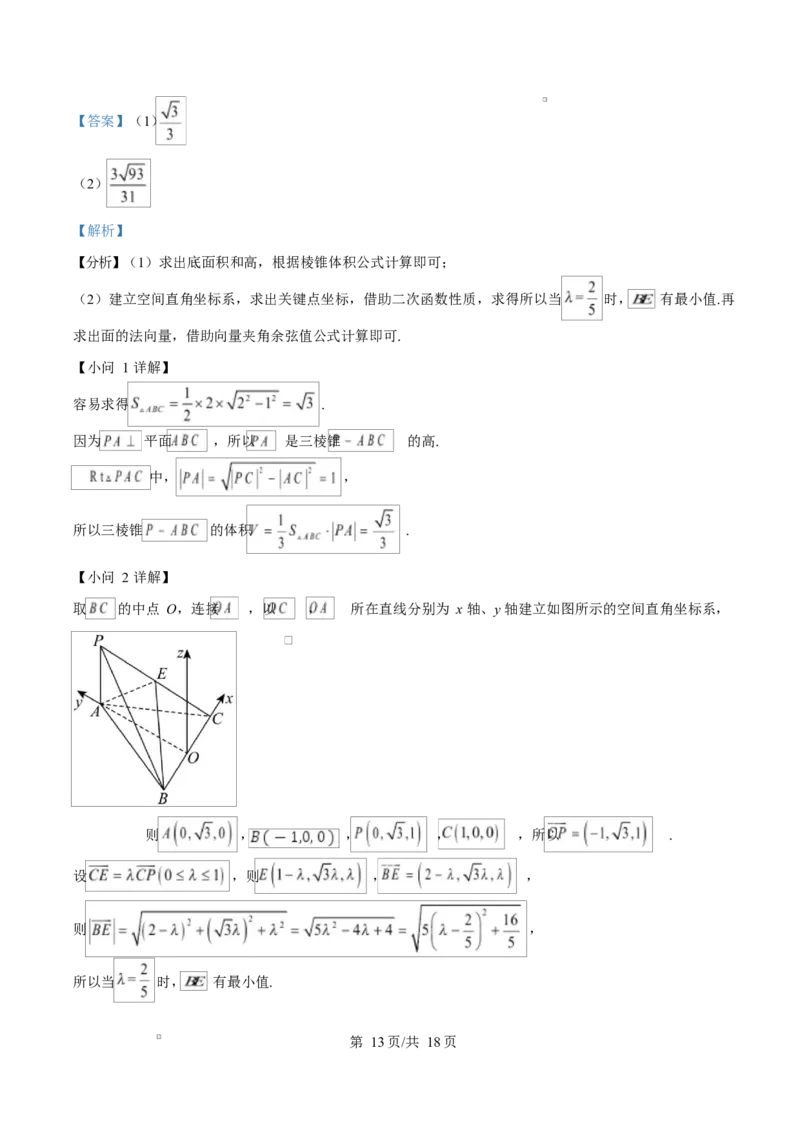
取 的中点 O,连接 ,以 , 所在直线分别为 x 轴、y 轴建立如图所示的空间直角坐标系,
则 , , , ,所以 .
设 ,则 , ,
则 ,
所以当 时, 有最小值.
第 13页/共 18页
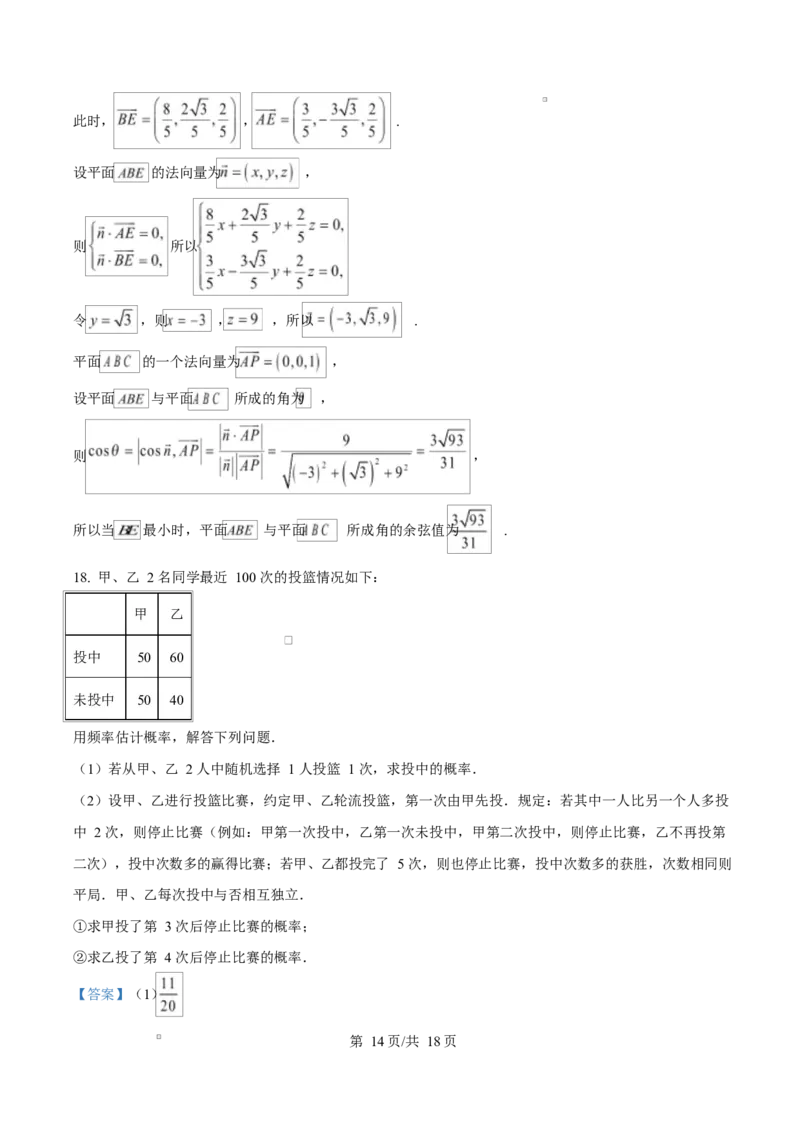
学科网(北京)股份有限公司此时, , .
设平面 的法向量为 ,
则 所以
令 ,则 , ,所以 .
平面 的一个法向量为 ,
设平面 与平面 所成的角为 ,
则 ,
所以当 最小时,平面 与平面 所成角的余弦值为 .
18. 甲、乙 2 名同学最近 100 次的投篮情况如下:
甲 乙
投中 50 60
未投中 50 40
用频率估计概率,解答下列问题.
(1)若从甲、乙 2 人中随机选择 1 人投篮 1 次,求投中的概率.
(2)设甲、乙进行投篮比赛,约定甲、乙轮流投篮,第一次由甲先投.规定:若其中一人比另一个人多投
中 2 次,则停止比赛(例如:甲第一次投中,乙第一次未投中,甲第二次投中,则停止比赛,乙不再投第
二次),投中次数多的赢得比赛;若甲、乙都投完了 5 次,则也停止比赛,投中次数多的获胜,次数相同则
平局.甲、乙每次投中与否相互独立.
①求甲投了第 3 次后停止比赛的概率;
②求乙投了第 4 次后停止比赛的概率.
【答案】(1)
第 14页/共 18页
学科网(北京)股份有限公司(2)① ;②
【解析】
【分析】(1)利用频率求出两人投中的概率,然后根据两人的投中概率可求答案;
(2)①先明确甲投了第 3 次后停止比赛的所有情况,结合互斥事件的概率求解;②乙投了第 4 次后停止比
赛,说明乙比甲多投中 2 次,按照轮次情况,分类求解概率即可.
【小问 1 详解】
甲同学 投篮命中率为 ,
乙同学的投篮命中率为 .
从甲、乙中随机选择 1 人投篮 1 次,投中的概率为 .
【小问 2 详解】
①甲投了 3 次,则乙投了 2 次.
由题意可得甲比乙多投中 2 次,有 2 种情况.
第一种情况:甲投中了 3 次,乙投中了 1 次,即甲每次投篮都投中,乙第一次投篮投中,第二次投篮没投
中,其概率为 .
第二种情况:甲投中了 2 次,乙投中了 0 次,即甲第一、三次投篮投中,第二次投篮没投中,乙每次投篮
都 没 投 中 , 或 甲 第 二 、 三 次 投 篮 投 中 , 第 一 次 投 篮 没 投 中 , 乙 每 次 投 篮 都 没 投
中 , 其 概 率 为
,
故所求概率为 .
②乙投了 4 次,则甲投了 4 次.
记甲、乙各投 1 次为一轮,则甲、乙共投了四轮.
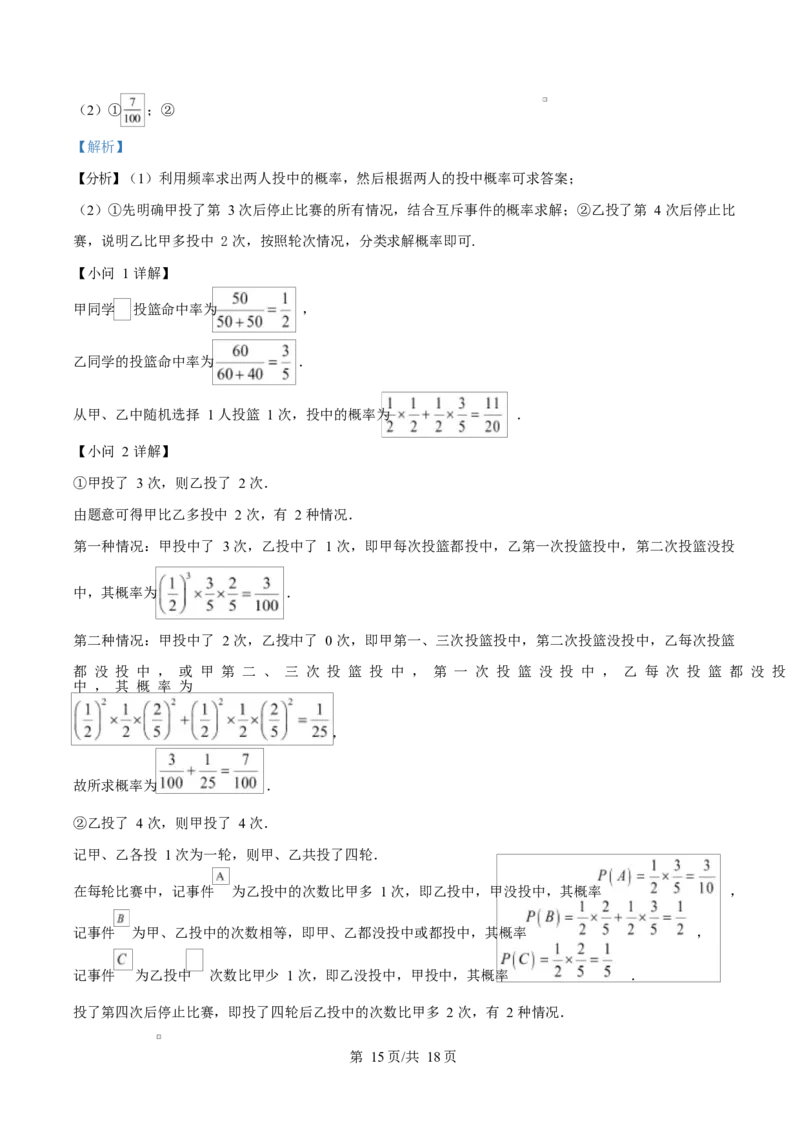
在每轮比赛中,记事件 为乙投中的次数比甲多 1 次,即乙投中,甲没投中,其概率 ,
记事件 为甲、乙投中的次数相等,即甲、乙都没投中或都投中,其概率 ,
记事件 为乙投中 次数比甲少 1 次,即乙没投中,甲投中,其概率 .
投了第四次后停止比赛,即投了四轮后乙投中的次数比甲多 2 次,有 2 种情况.
第 15页/共 18页
学科网(北京)股份有限公司第一种情况:四轮比赛中,事件 各发生 2 次,即第一至四轮依次为 或 , 或
,其概率为 .
第二种情况:四轮比赛中,事件 发生 3 次,事件 发生 1 次,即第一至四轮依次为 , 或
,其概率为 .
所求概率为 .
19. 已知 为坐标原点,椭圆 : 的左顶点为 A,右焦点为 F,点 B 在 C 上,且
, ,直线 与直线 的斜率之比为 3.
(1)求椭圆 C 的标准方程;
(2)过点 F 的直线 , 分别与 C 交于点 D,E 和点 M,N,若 P,Q 分别为线段 和 的中点,当
直线 , 的斜率之积为 时,求 的面积的最大值.
【答案】(1)
(2)
【解析】
【分析】(1)首先根据对称性,设两直线的斜率,求出 ,再求出 , , .再求
出 .
(2)设直线 的方程为 , , ,联立得
,求出 ,再求出 的中点为 .再求
出 的面积.
【小问 1 详解】
根据对称性,不妨设点 在第一象限.
第 16页/共 18页
学科网(北京)股份有限公司记直线 与直线 的斜率分别为 , ,
, .
由题意可得 ,
所以
,解得 , , .
故椭圆 C 的标准方程为 .
【小问 2 详解】
显然直线 , 的斜率存在且不为 0.
设直线 的方程为 , , ,
联立 得 ,
所以 , ,
则 , , .
同理 , , ,
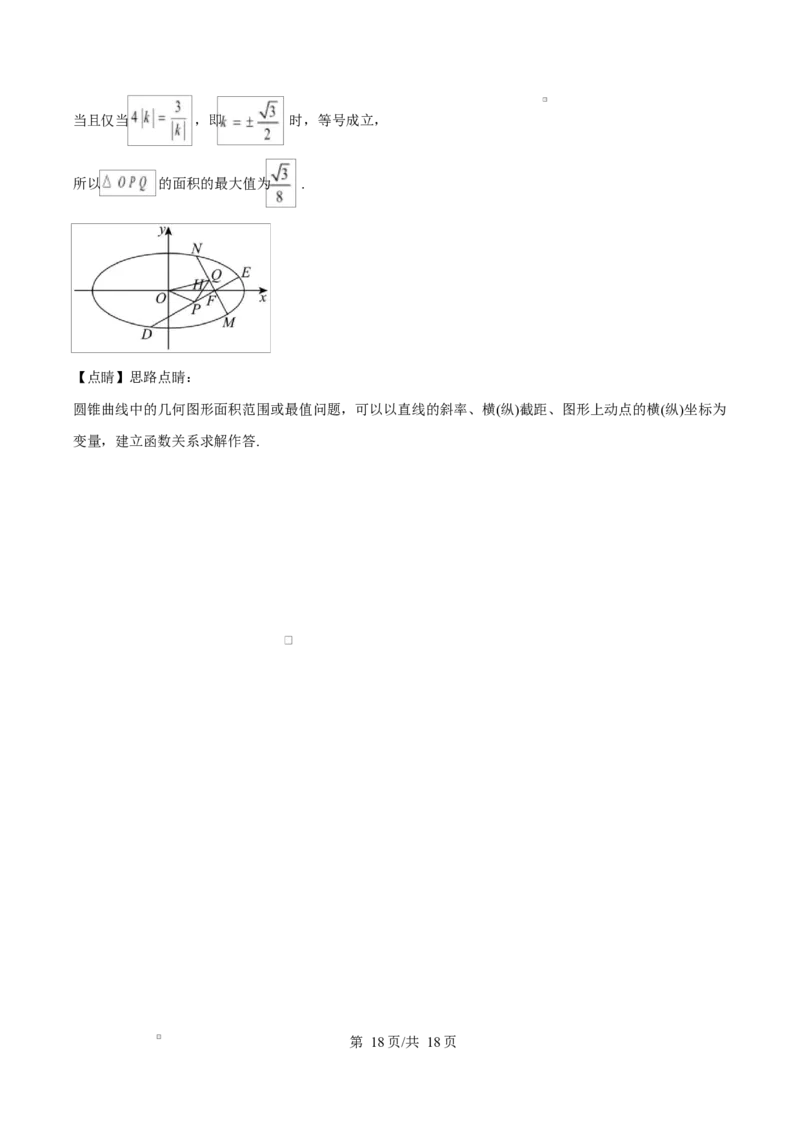
所以 的中点为 .
的面积 ,
第 17页/共 18页
学科网(北京)股份有限公司当且仅当 ,即 时,等号成立,
所以 的面积的最大值为 .
【点睛】思路点睛:
圆锥曲线中的几何图形面积范围或最值问题,可以以直线的斜率、横(纵)截距、图形上动点的横(纵)坐标为
变量,建立函数关系求解作答.
第 18页/共 18页