文档内容
2024 年高三年级期初调研检测
数学试题
2024.09
本试卷共 4页,19题.全卷满分 150分.考试用时 120分钟.
注意事项:
1.答卷前,考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上,并将准考证
号条形码粘贴在答题卡上的指定位置.
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需要
改动,用橡皮擦干净后,再选涂其它答案标号.回答非选择题时,将答案写在答题卡上.写在
本试卷上无效.
3.考试结束后,将本试卷和答题卡一并交回.
一、选择题:本题共 8小题,每小题 5分,共 40分.在每小题给出的四个选项中,只有一项
是符合题目要求的.
A= { x y =ln ( 4−x )} B={ 1,2,3,4,5 } AB =
1. 已知集合 , ,则 ( )
A. {5} B. {1,2,3} C. {1,2,3,4} D. {1,2,3,4,5}
2. 已知复数z满足 ( 1+2i ) z =4+3i,则z的虚部为( )
A. 1 B. −1 C. i D. −i
π π
3. 已知命题p:∀α∈R,sin −α =cos +α ,则¬p为( )
4 4
π π π π
A. ∀α∈R,sin −α ≠cos +α B. ∃α∈R,sin −α ≠cos +α
4 4 4 4
π π π π
C. ∀α∉R,sin −α =cos +α D. ∃α∉R,sin −α =cos +α
4 4 4 4
4. 等差数列 的首项为−1,公差不为0,若a ,a ,a 成等比数列,则 的前6项和为( )
2 3 6
{𝑎𝑎𝑛𝑛} {𝑎𝑎𝑛𝑛}
A. −1 B. 3 C. −24 D. 24
5. 在平面直角坐标系 xOy 中,角 α 与角 β 均以 x 轴的非负半轴为始边,它们的终边关于 x 轴对称.若
1
cosα=− ,则cos (α−β)=( )
3
第1页/共4页
学科网(北京)股份有限公司1 7 7
A. B. − C. 1 D.
9 9 9
6. 两个粒子A,B从同一发射源发射出来,在某一时刻,它们的位移分别为S =(1,2),S =(4,3).粒子
A B
B相对粒子A的位移为S,则S在S 上的投影向量为( )
A
5 2 5 ( )
A. , B. 5,2 5 C. (1,2) D. (2,1)
5 5
( x+a )2 ,x≤0
7. 设 f
(
x
)=
1 ,若 f
(
0
)
是 f
(
x
)
的最小值,则a的取值范围为( )
x+ +a,x>0
x
A. [−1,0 ] B. [−1,2 ] C. [−2,−1 ] D. [−2,0 ]
x2 y2
8. 已知双曲线C: − =1(a >0,b>0)的左、右焦点分别为F ,F .以F F 为直径的圆和C的渐近线
1 2 1 2
a2 b2
在第一象限交于A点,直线AF 交C的另一条渐近线于点B,FB= BA,则C的离心率为( )
1 1
A. 2 B. 3 C. 2 D. 3
二、选择题:本题共 3小题,每小题 6分,共 18分.在每小题给出的四个选项中,有多项符
合题目要求.全部选对的得 6分,部分选对的得部分分,有选错的得 0分.
9. 一组数据:x ,x ,…,x 是公差为-2的等差数列,去掉首末两项x ,x 后得到一组新数据,则( )
1 2 10 1 10
A. 两组数据的极差相同 B. 两组数据的中位数相同
C. 两组数据的平均数相同 D. 两组数据的标准差相同
10. 平面α过正方体ABCD− ABC D 的顶点A,平面α//平面CBD ,平面α平面ABCD=m,平
1 1 1 1 1 1
面α平面ABB A =n,则( )
1 1
π
A. BD //m B. AB//平面α C. n⊥平面ADC B D. m,n所成的角为
1 1 1 1 1
3
m 1+a
11. 设数列 和 的项数均为m,称∑ a −b 为数列 和 的距离.记满足a = n 的所有数
i i n+1 1−a
i=1 n
{𝑎𝑎𝑛𝑛} {𝑏𝑏𝑛𝑛} {𝑎𝑎𝑛𝑛} {𝑏𝑏𝑛𝑛}
列 构成的集合为C.已知数列 { A } 和 { B } 为C中的两个元素,项数均为m,下列正确的有( )
n n
{𝑎𝑎𝑛𝑛}
A. 数列1,3,5,7和数列2,4,6,8的距离为4
( )
B. 若m=4p p∈N* ,则AA A = BB B
1 2 m 1 2 m
第2页/共4页
学科网(北京)股份有限公司m
C. 若m=4p ( p∈N* ) ,则∑ A ≤m
i
i=1
D. 若A =2,B =3,数列 { A } 和 { B } 的距离小于2017,则m的最大值为3456
1 1 n n
三、填空题:本题共 3个小题,每小题 5分,共 15分.
12. 若曲线y =axcosx在点 ( 0,0 ) 处的切线斜率为−1,则a= ______.
π
13. 若x = ,x =π是函数 f ( x )=sinωx (ω>0 ) 的两个相邻极值点,则ω= ______.
1 3 2
14. 正方体ABCD-ABC D 的棱长为3,P是侧面ADD A(包括边界)上一动点,E是棱CD上一点,
1 1 1 1 1 1
若∠APB=∠DPE,且△APB的面积是DPE面积的9倍,则三棱锥P-ABE体积的最大值是______.
四、解答题:本题共 5小题,共 77分.解答应写出文字说明,证明过程或演算步骤.
15. 甲、乙两人在每次猜谜活动中各猜一个谜语,若一方猜对且另一方猜错,则猜对的一方获胜,否则本次
2 1
平局.已知每次活动中,甲、乙猜对的概率分别为 和 ,且每次活动甲、乙猜对与否互不影响,各次活
3 2
动也互不影响.
(1)求在一次猜谜活动中,有一方获胜的概率;
(2)若有一方获胜则猜谜活动结束,否则猜谜继续,猜谜最多进行3次,求猜谜次数X的分布列和期
望.
a
16. 已知ABC的内角A,B,C 的对边分别为a,b,c, 2 ( ccosB+bcosC )= .
cosA
(1)求A;
1
(2)若AB边上的高等于 c,求sinC.
3
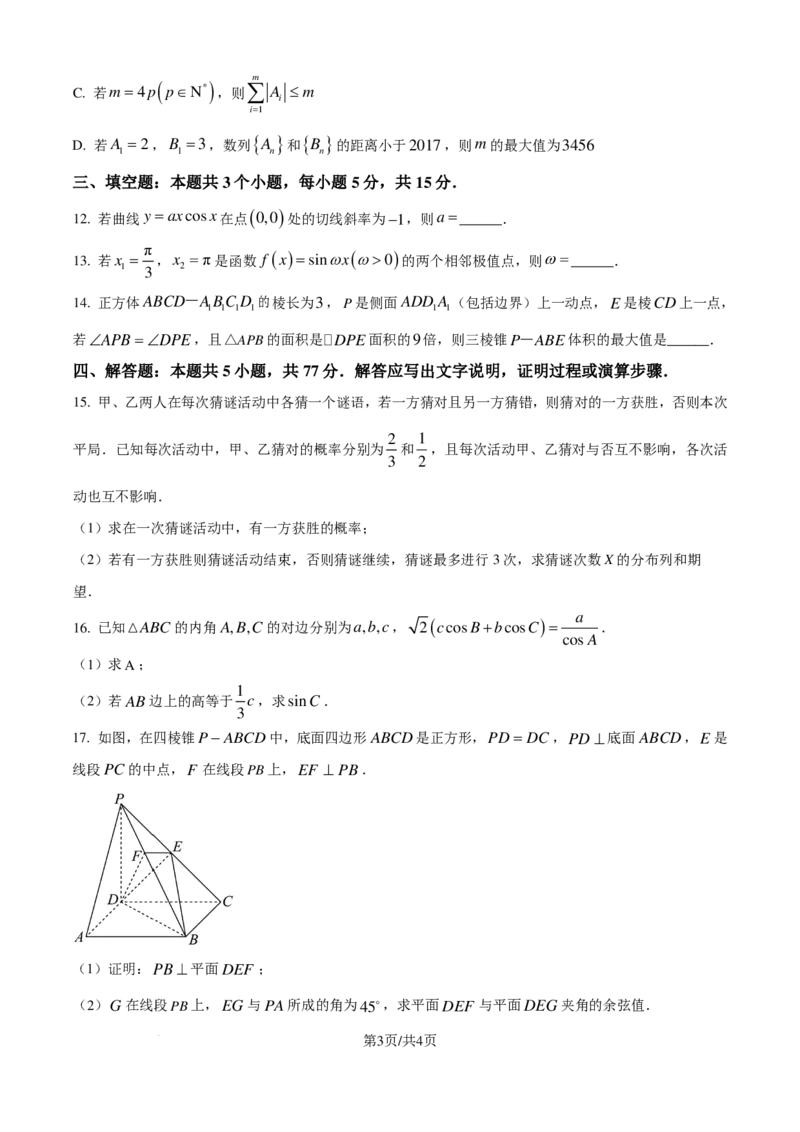
17. 如图,在四棱锥P−ABCD中,底面四边形ABCD是正方形,PD= DC,PD⊥底面ABCD,E是
线段PC的中点,F 在线段PB上,EF ⊥ PB.
(1)证明:PB⊥平面DEF ;
(2)G在线段PB上,EG与PA所成的角为45,求平面DEF 与平面DEG夹角的余弦值.
第3页/共4页
学科网(北京)股份有限公司18. 已知双曲线C:4x2 − y2 =m,点P(1,1)在C上.按如下方式构造点P(n≥2);过点P 作斜率为1
1 n n−1
的直线与C的左支交于点Q ,点Q 关于 y轴的对称点为P ,记点P 的坐标为 ( x ,y ) .
n−1 n−1 n n n n
(1)求点P,P 的坐标;
2 3
(2)记a =2x − y ,证明:数列 { a } 为等比数列;
n n n n
(3)O为坐标原点,G,H 分别为线段PP ,P P 的中点,记△OP P ,OGH 的面积分别为
n n+2 n+1 n+3 n+1 n+2
S
S ,S ,求 1 的值.
1 2 S
2
19. 已知函数 f ( x ) 定义域为I ,D⊆ I ,若∀x∈D,∃t∈D,当x