文档内容
2025 年高三第一次模拟考试试
A卷 答
题 数学参考答案
1.A【 解析】本题考查复数的运算与共轭复数,考查数学运算的核心素养.
因为 ,所以
2.C【 解析】本题考查集合的交集,考查数学运算的核心素养.
依题意可得A∩B={-√2,√3,√5}, 则 A∩B 的元素个数为3.
3.A【 解析】本题考查平面向量的平行与对数的运算,考查数学运算的核心素
养. 因为a//b,所以2×( - 6)= - 4lgm,lg m=3,则 m=10³=1000.
4.B【 解析】本题考查排列组合与古典概型的实际应用,考查应用意识.
因为甲、乙同时站两端的概率为 ,所以甲、乙不同时站两端的概率为
5.D【 解析】本题考查导数在研究函数单调性上的应用,考查逻辑推理的核心素养.
依题意可得f'(x)=3ax²-2x≤0 对 x∈[-6,-4] 恒成立,则 对 x∈[-6,-4] 恒
成 立.当x ∈[-6,-4] 时,函数 ,所以
a≤
6.D【 解析】本题考查函数的奇偶性与不等式的解集,考查逻辑
推 理与直观想象的核心素养.
因为f(x) 为定义在R 上的奇函数,所以f(0)=0. 又 f(1)=
f(4)=0, 所以f(-1)=f(-4)=0. 根据题意作出f(x) 的大致
图象,如图所示, 由图可
等 价 于 或
得x∈[-4,-1]U[0,1]U[3,4].
7.B【 解析】本题考查双曲线的离心率、正弦定理与三角恒等变换,考查直观想象与数学运
算 的核心素养.
依题意得∠PF₂F₁=180°-20°-60°=100°,C 的离心率
8.D【 解析】本题考查基本不等式,考查逻辑推理的核心素养.
【高三数学 ·参考答案第1页(共6页)】设 .因为x 为正数,所以
, 即
时,等号成立,则 .因为y 为正数,所以:
,即y=3 时,等号成立,则 .所以M≥3, 则: 的最小值
当
为
9.BC【 解析】本题考查曲线方程,考查逻辑推理的核心素养.
取a=b=1, 得x²+y²=2x+y, 即( ,A 错误.
当a=b=0 时,该方程为x=0,B 正确.当a=0 且 b(b+1)≠0 时, ,曲线C 的 准
线方程是 ,C 正确. 当a≠0,b=0 时,该方程为ax²=x+ay, 即
,曲线C 关于直线 对称,D 错误.
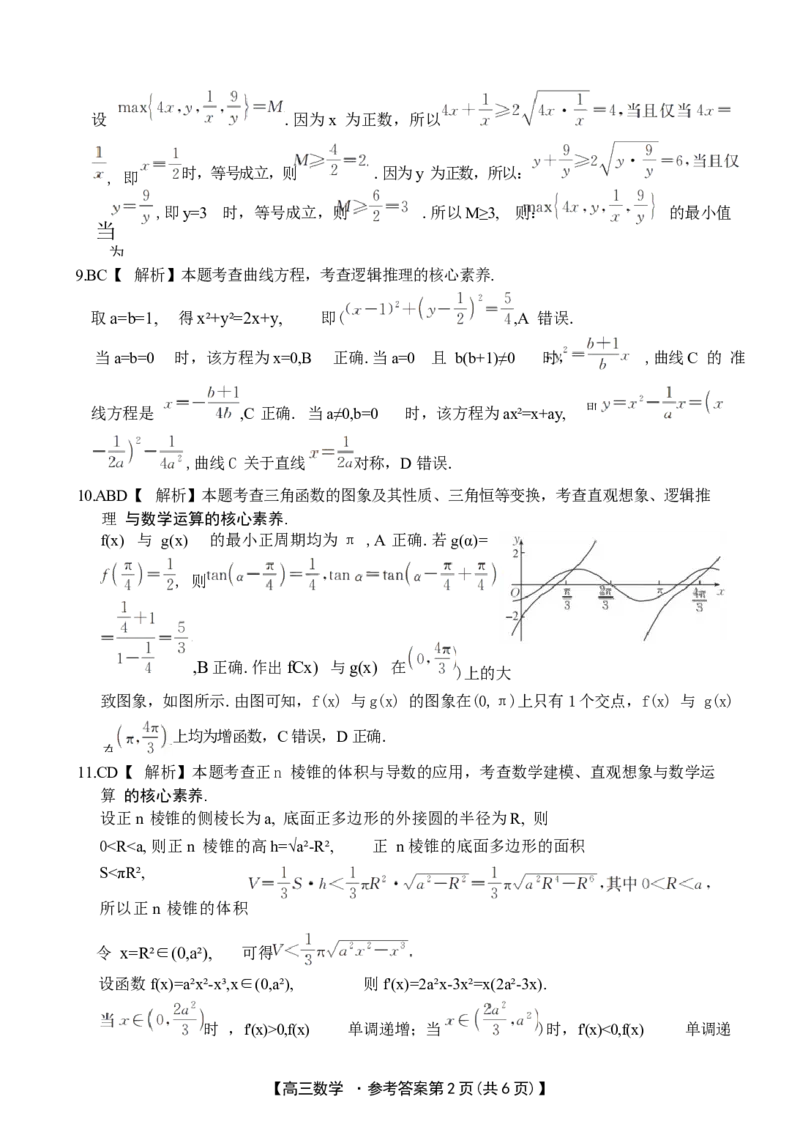
10.ABD【 解析】本题考查三角函数的图象及其性质、三角恒等变换,考查直观想象、逻辑推
理 与数学运算的核心素养.
f(x) 与 g(x) 的最小正周期均为π ,A 正确.若g(α)=
, 则
,B正确.作出fCx) 与g(x) 在
)上的大
致图象,如图所示.由图可知,f(x) 与g(x) 的图象在(0,π)上只有1个交点,f(x) 与 g(x)
上均为增函数,C 错误,D 正确.
在
11.CD【 解析】本题考查正n 棱锥的体积与导数的应用,考查数学建模、直观想象与数学运
算 的核心素养.
设正n 棱锥的侧棱长为a, 底面正多边形的外接圆的半径为R, 则
00,f(x) 单调递增;当 )时,f'(x)<0,f(x) 单调递
【高三数学 ·参考答案第2页(共6页)】减.可知 , 则 ,解得a>6.
12.相交【解析】本题考查直线与圆的位置关系以及余弦定理,考查数学运算与逻辑推理的核
心素养.
由题意可知a²+b²-c²>0, 则 c<√a²+b², 圆x²+y²=1 的圆心到直线ax+by+c=0 的
距离 ,所以直线ax+by+c=0 与 圆x²+y²=1 相交.
13 .2或3【解析】本题考查统计中的百分位数与极差,考查数据处理能力.
将数据 1,1,2,3,1 按照从小到大的顺序排列为 1,1,1,2,3,因为 7×60%=4.2,且数据
1,1, 2,3,m,2m,1 的第60百分位数为2,所以m=1 或2 . 当m=1 时,这组数据的
极差为3-1 =2;当m=2 时,这组数据的极差为4-1=3.故这组数据的极差为2或3.
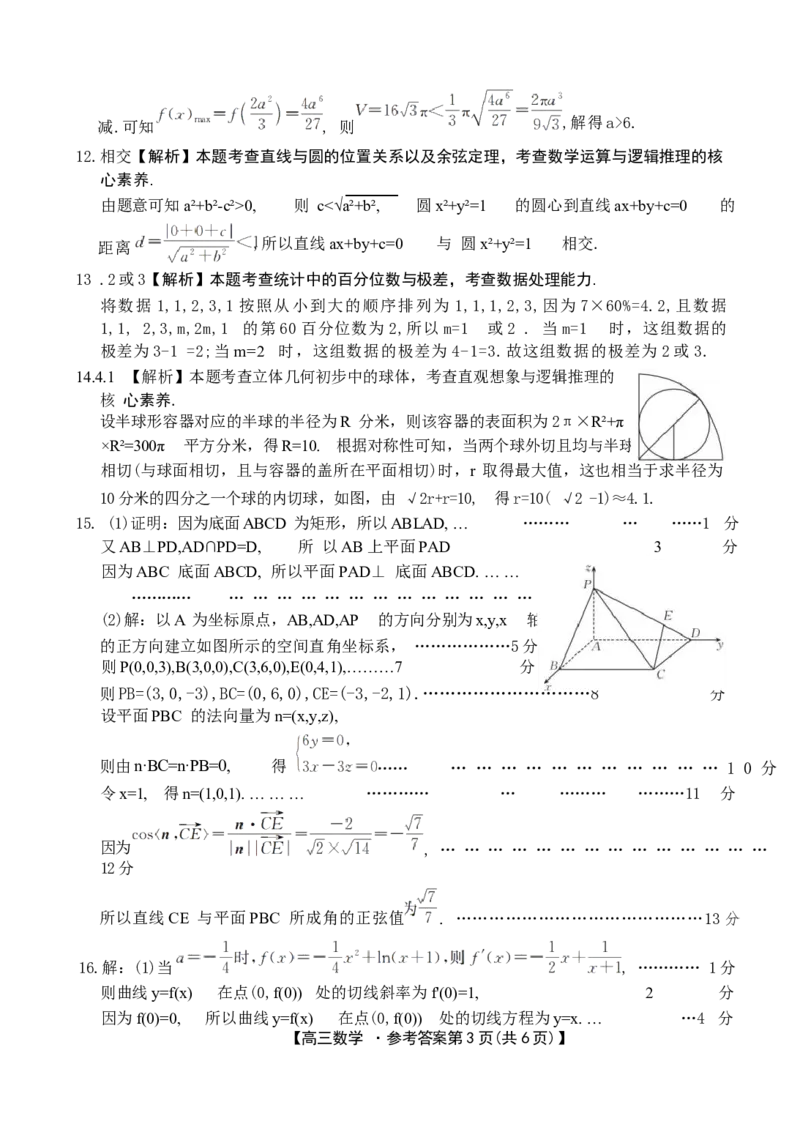
14.4.1 【解析】本题考查立体几何初步中的球体,考查直观想象与逻辑推理的
核 心素养.
设半球形容器对应的半球的半径为R 分米,则该容器的表面积为2π×R²+π
×R²=300π 平方分米,得R=10. 根据对称性可知,当两个球外切且均与半球
相切(与球面相切,且与容器的盖所在平面相切)时,r 取得最大值,这也相当于求半径为
10分米的四分之一个球的内切球,如图,由 √2r+r=10, 得r=10( √2 -1)≈4.1.
15. (1)证明:因为底面ABCD 为矩形,所以ABLAD, … ……… … ……1 分
又AB⊥PD,AD∩PD=D, 所 以AB 上平面PAD 3 分
因为ABC 底面ABCD, 所以平面PAD⊥ 底面ABCD. … …
………… … … … … … … … … … … … … … … … 4分
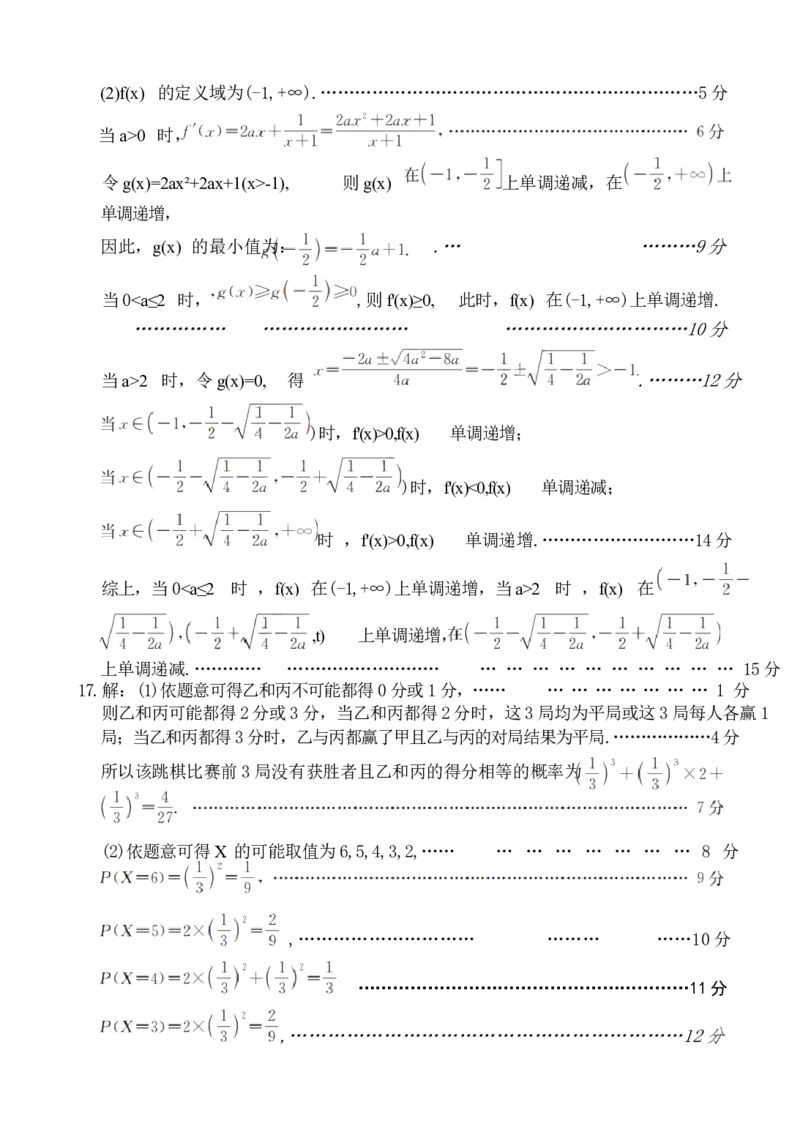
(2)解:以A 为坐标原点,AB,AD,AP 的方向分别为x,y,x 轴
的正方向建立如图所示的空间直角坐标系, ………………5分
则P(0,0,3),B(3,0,0),C(3,6,0),E(0,4,1),………7 分
则PB=(3,0,-3),BC=(0,6,0),CE=(-3,-2,1).…………………………8 分
设平面PBC 的法向量为n=(x,y,z),
则由n·BC=n·PB=0, 得 …… … … … … … … … … … … … 1 0 分
令x=1, 得n=(1,0,1). … … … ………… … ……… ………11 分
因为 , … … … … … … … … … … … … … …
12分
所以直线CE 与平面PBC 所成角的正弦值 . ………………………………………13分
16.解:(1)当 , ………… 1分
则曲线y=f(x) 在点(0,f(0)) 处的切线斜率为f'(0)=1, 2 分
因为f(0)=0, 所以曲线y=f(x) 在点(0,f(0)) 处的切线方程为y=x. … …4 分
【高三数学 ·参考答案第3页(共6页)】(2)f(x) 的定义域为(-1,+∞).…………………………………………………………5分
当a>0 时,
令g(x)=2ax²+2ax+1(x>-1), 则g(x) 上单调递减,在
单调递增,
因此,g(x) 的最小值为: .… ………9分
当02 时,令g(x)=0, 得 .………12分
)时,f'(x)>0,f(x) 单调递增;
)时,f'(x)<0,f(x) 单调递减;
时 ,f'(x)>0,f(x) 单调递增.………………………14分
综上,当02 时 ,f(x) 在
,t) 上单调递增,
上单调递减.………… ……………………… … … … … … … … … … … 15分
17.解:(1)依题意可得乙和丙不可能都得0分或1分,…… … … … … … … … 1 分
则乙和丙可能都得2分或3分,当乙和丙都得2分时,这3局均为平局或这3局每人各赢1
局;当乙和丙都得3分时,乙与丙都赢了甲且乙与丙的对局结果为平局.………………4分
所以该跳棋比赛前3局没有获胜者且乙和丙的得分相等的概率为
(2)依题意可得X 的可能取值为6,5,4,3,2,…… … … … … … … … 8 分
,………………………… ……… ……10分
…………………………………………………11分
,………………………………………………………12分【高三数学 ·参考答案第4页(共6页)】………………………………………………………………… 13分
则X的分布列为
X 6 5 4 3 2
P
………………………………………………………………………………………… 14
分
…………………………………
15
分
18.解:(1)当n≥2时,S,=2+(2+4+…+2 n-2)+(2+…+2"-¹) ………………………1 分
………………………………………………… 2 分
=2"+ n ²-n ……………………………………………………………………………… 3 分
又 S₁= a ₁=2也满足S,=2”+ n²-n,
所以S,=2”+ n ²-n ………………………………………………………………………4 分
因为S ,+ b =- n +2,且S 。+1+bn+1-( S,+ bn)=-1,
所以{S,}与{bn}互为和等差数列…………………………………………………………5 分
(2)因为S ,=2 an + n ,所以S ₁=2 a ₁+1,得a ₁=-1 ………………………………………6 分
因为S ,=2 an + n ,所以当n≥2时,an = S ,- S ,-1=2 a ,-2 an-1+1,
即a,=2an-1-1 ……………………………………………………………………………7 分
所以an -1=2( an-1-1) ……………………………………………………………………8 分
又a₁-1=-2,所以数列{a ,-1}是首项为-2,公比为2的等比数列……………………9 分
所以an -1=-2×2“-¹=-2”,即an =1-2” ……………………………………………10分
①因为{an }与{b }互为和等差数列,所以{1-2"+bn }为等差数列,
又{bn}为等比数列,所以{b,}的通项公式为b,=2” ………………………………………11分
②cn=(1-2”)³-(2”)³=1-3×2”+3×4”-2×8” ……………………………………13分
故
………………………………………………… 17分
19. (1)解:因为椭圆( 的离心率 , 所以 ……………… 1 分
解得a =4 ……………………………………………………………………………………2 分
所以C 的长轴长为2 √a =4 ……………………………………………………………… 3 分
(2) 证明:设直线l : x = my+4, M(x ₁, y1), N (x 2, y 2).
得(3m²+4)y²+24my+36=0 ……………………………………… 4 分【高三数学 ·参考答案 第5页(共6页)】则△=144(m²-4)>0, 得m²>4, 5 分
,…………… …………………………6分
设直线BM,BN 的斜率分别为k₁,kz,
所以直线BM,BN 的斜率之和为定值0. ………… ……………………………8分
(3)解:设M(x₁,y₁),N(x₂,y2),P(x₃,ys),Q(x₄,y₄),AP=aAM,AQ=μAN,x>0 且
λ≠1,μ>0且μ≠1,
则 ………… … … … 9 分
代入得-(x₃+λx₁)=1+λ, 与x₃-ax₁=-4(1-λ) 联立,
解得 同理可 ……………………………… ……11分
,贝
又直线l 过 , ……… …… …………… 12分
并化简可得
代 入
设直线PQ 过定点E(x%,yó),
则 代入数据并化简可得
, … … … … … … … … … 1 6 分
对比系数可 ,解
得
… … … … … … … 1 7 分
… … …
则直线PQ 过定点! . … …
【高三数学 ·参考答案第6页(共6页)】