文档内容
广东省清远市2025-2026学年高二上学期期中考试数学试卷
一、单选题
1.直线 经过两点 ,则 的斜率为( )
A. B. C. D.
2.已知向量 ,若 与 垂直,则 ( ).
A. B. C. D.
3.圆 与圆 的位置关系为( )
A.外离 B.外切 C.相交 D.内切
4.棱长为2的正四面体ABCD中,点E是AD的中点,则 ( )
A.1 B.-1 C. D.
5.如图,在正方体 中,点 在线段 上,点 在线段 上,且
,则 与 所成角的余弦值为( )A. B. C. D.
6.“ ”是“直线 和直线 平行”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
7.已知直线 ,若直线 与圆 交于 两点,则 的最小
值为( )
A. B.2 C. D.4
8.在平面直角坐标系中,点 的坐标为 ,圆 ,点 为 轴上一动点.现
由点 向点 发射一道粗细不计的光线,光线经 轴反射后与圆 有交点,则 的取值范围为( )
A. B. C. D.
二、多选题
9.下列说法中,正确的有( )
A.直线 在y轴上的截距为-2 B.直线 的倾斜角为120°
C.直线 (m∈R)必过定点(0,-3) D.点(5,-3)到直线y+2=0的距离为7
10.关于空间向量,以下说法正确的是( )
A.若直线l的方向向量为 ,平面 的一个法向量为 ,则
B.若空间中任意一点O,有 ,则 四点共面
C.若空间向量 , 满足 ,则 与 夹角为钝角
D.若空间向量 , ,则 在 上的投影向量为A B C D
1 1 1 1
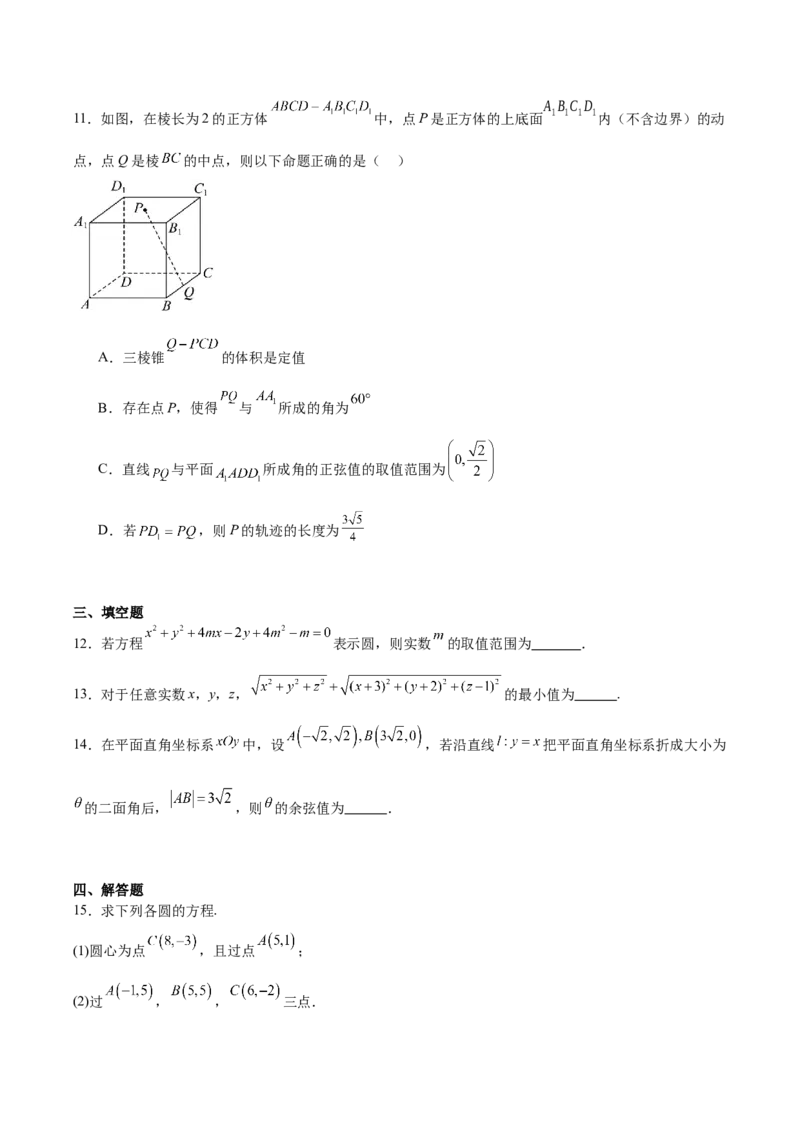
11.如图,在棱长为2的正方体 中,点P是正方体的上底面 内(不含边界)的动
点,点Q是棱 的中点,则以下命题正确的是( )
A.三棱锥 的体积是定值
B.存在点P,使得 与 所成的角为
C.直线 与平面 所成角的正弦值的取值范围为
D.若 ,则P的轨迹的长度为
三、填空题
12.若方程 表示圆,则实数 的取值范围为 .
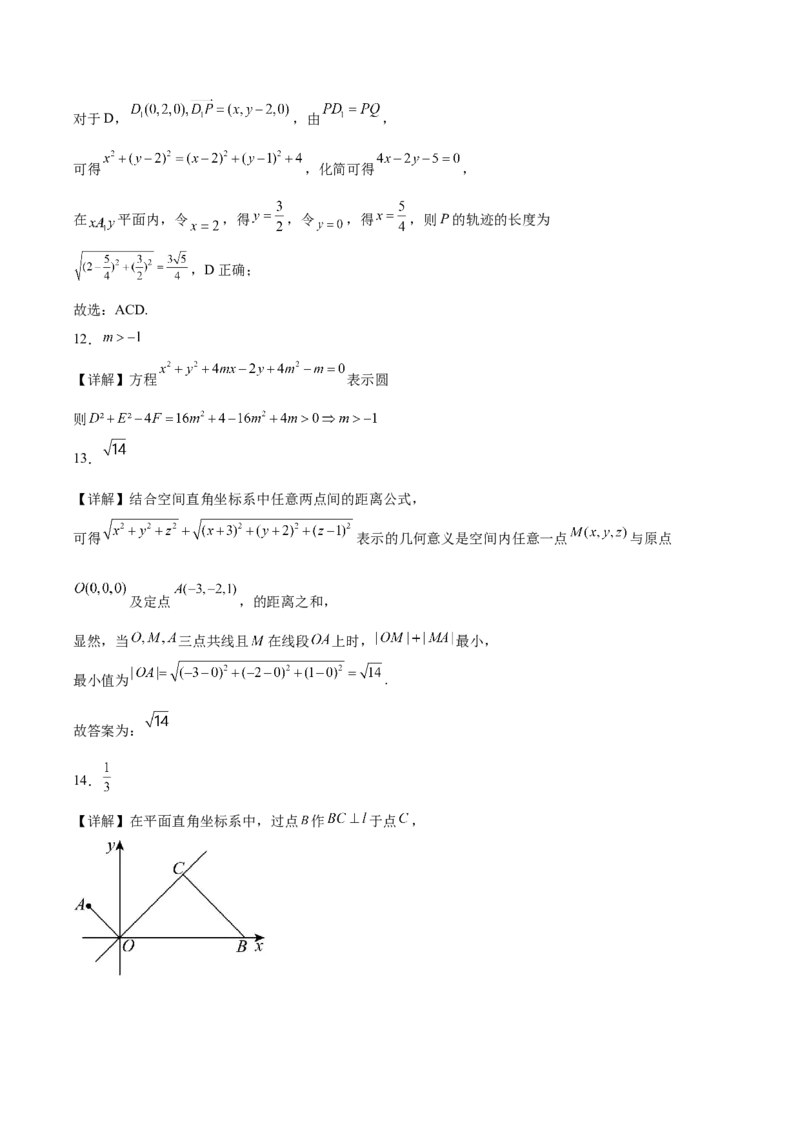
13.对于任意实数x,y,z, 的最小值为 .
14.在平面直角坐标系 中,设 ,若沿直线 把平面直角坐标系折成大小为
的二面角后, ,则 的余弦值为 .
四、解答题
15.求下列各圆的方程.
(1)圆心为点 ,且过点 ;
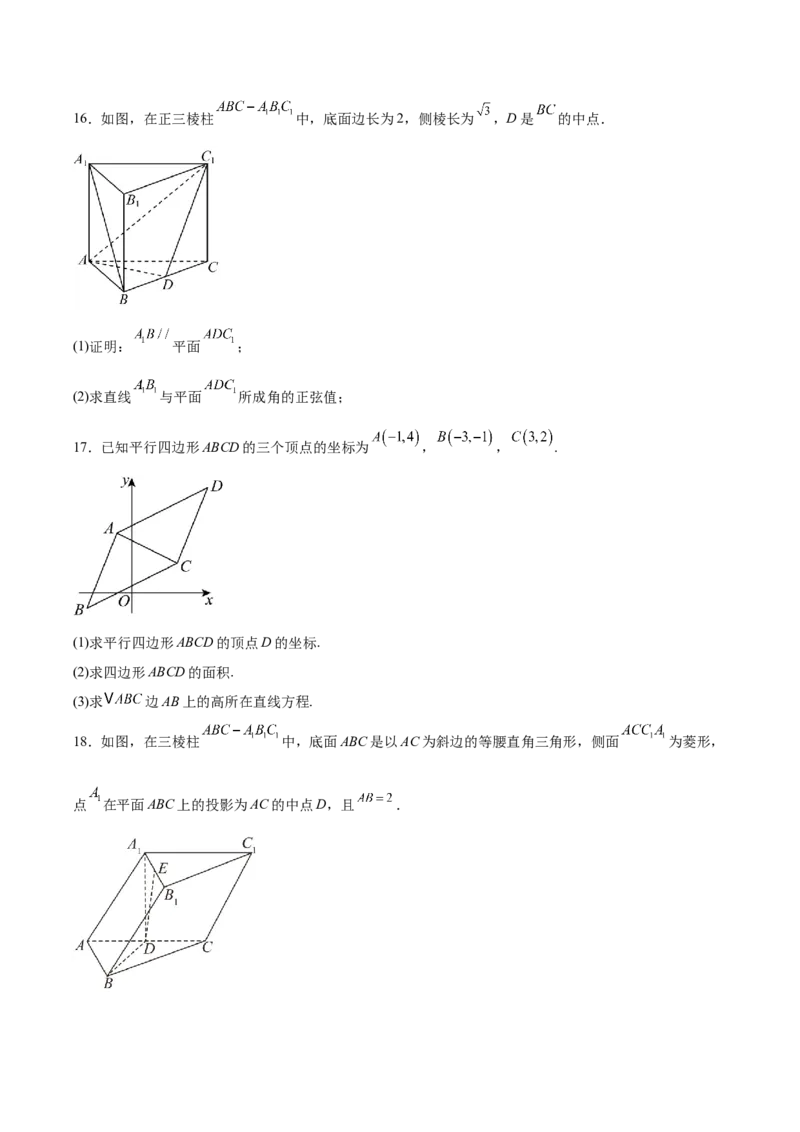
(2)过 , , 三点.16.如图,在正三棱柱 中,底面边长为2,侧棱长为 ,D是 的中点.
(1)证明: 平面 ;
(2)求直线 与平面 所成角的正弦值;
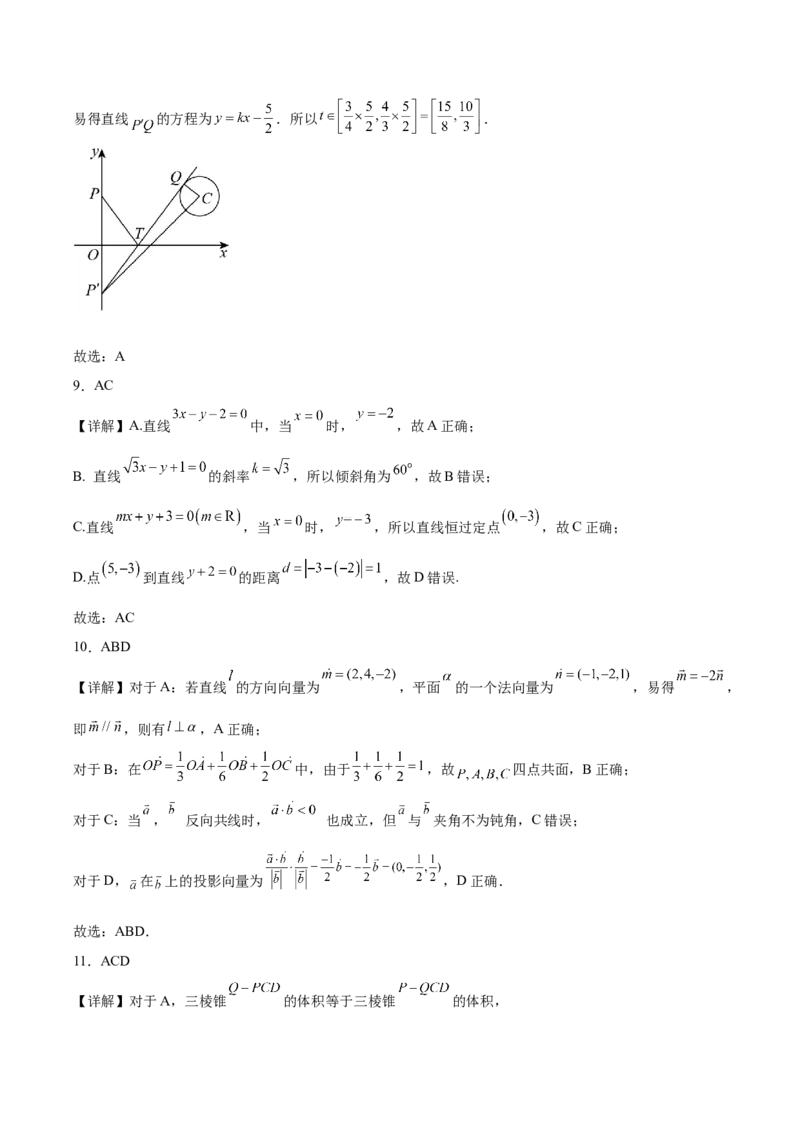
17.已知平行四边形ABCD的三个顶点的坐标为 , , .
(1)求平行四边形ABCD的顶点D的坐标.
(2)求四边形ABCD的面积.
(3)求 边AB上的高所在直线方程.
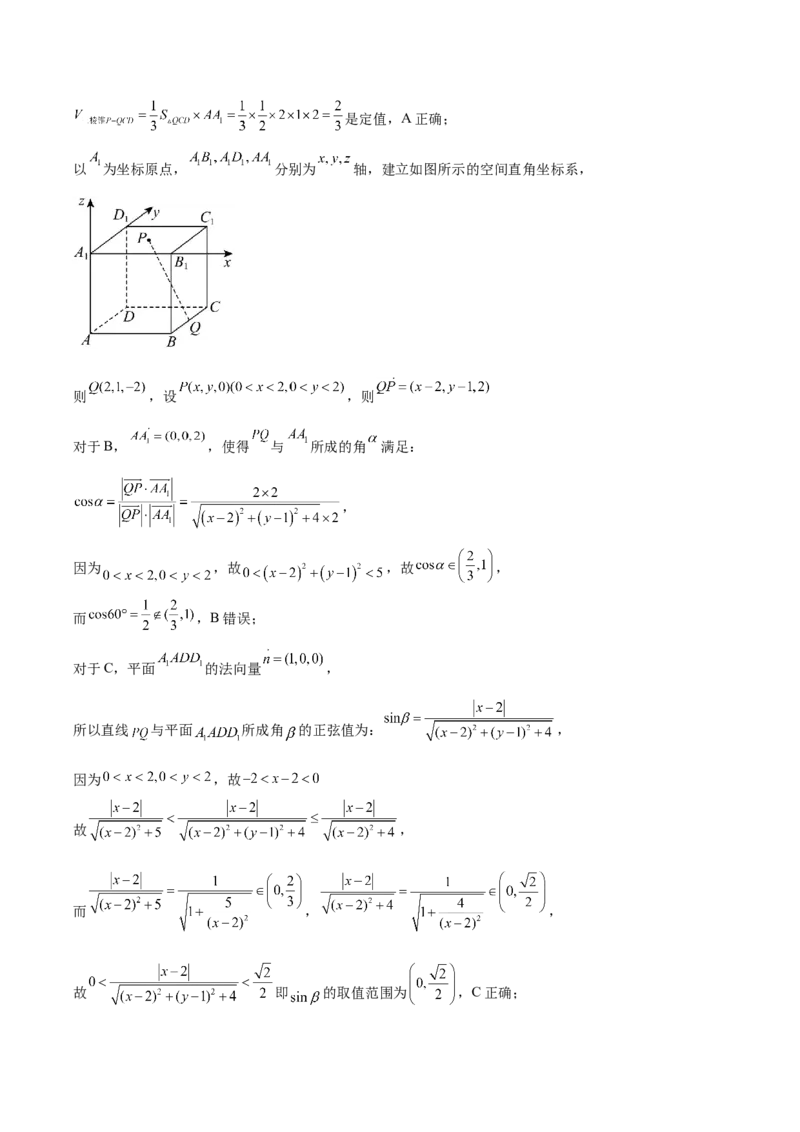
18.如图,在三棱柱 中,底面ABC是以AC为斜边的等腰直角三角形,侧面 为菱形,
点 在平面ABC上的投影为AC的中点D,且 .(1)求点C到侧面 的距离;
(2)在线段 上是否存在点E,使得直线DE与侧面 所成角的正弦值为 ?若存在,请求出
的长;若不存在,请说明理由.
19.已知定点 , ,动点 满足 .
(1)求动点 的轨迹 的方程;
(2)过点 作两条互相垂直的直线 与 ,直线 交曲线 于 , 两点,直线 交曲线 于 , 两点,
求四边形 面积的最大值.参考答案
1.A
【详解】由 ,得 的斜率为 .
故选:A
2.D
【详解】由于 与 垂直,所以 ,所以 ,
故 ,
故选:D
3.B
【详解】由题意,圆 ,则圆心 ,半径 ,
圆 ,则圆心 ,半径 ,
所以两圆圆心距 ,所以两圆外切.
故选:B.
4.A
【详解】 ,所以 .
故选:A.
5.D
【详解】设正方体 的棱长为1,
以 为原点,以 所在直线分别为 轴,建立如图所示空间直角坐标系,则 .
所以 ,即 与 所成角的余弦值为 .
故选:D
6.C
【详解】当 ,则直线分别为 和直线 满足平行,即充分性成立,
若直线 和直线 平行,
当 时,直线分别为 和 ,不满足条件,
当 时,满足 ,即 ,解得 或 ,
当 时,两直线重合,故不满足条件,故 ,即必要性成立,
综上“ ”是“直线 和直线 平行”的充要条件,
故选:C.
7.C
【详解】直线 ,即 ,
令 ,解得 ,
所以直线 过定点 ,
圆 的圆心 ,半径 ,
因为 ,所以点 在圆 内,
则圆心 到直线 的距离 ( 时取等号),
所以 ( 时取等号),
所以 的最小值为 .
故选:C.
8.A
【详解】方法一:作点 关于 轴的对称点 ,则直线 与圆 有交点.
又 ,所以直线 的方程为 ,即 .
由题知圆 的圆心为 ,半径为1,
直线 与圆 有交点,即圆心 到直线 的距离小于等于1,
所以 ,解得 .
方法二:作点 关于 轴的对称点 ,则直线 与圆 有交点,
临界情况为直线 与圆 相切.
设切点为 ,令 ,易得 ,
所以 .
因为直线 的斜率为 ,
所以直线 的斜率 .易得直线 的方程为 .所以 .
故选:A
9.AC
【详解】A.直线 中,当 时, ,故A正确;
B. 直线 的斜率 ,所以倾斜角为 ,故B错误;
C.直线 ,当 时, ,所以直线恒过定点 ,故C正确;
D.点 到直线 的距离 ,故D错误.
故选:AC
10.ABD
【详解】对于A:若直线 的方向向量为 ,平面 的一个法向量为 ,易得 ,
即 ,则有 ,A正确;
对于B:在 中,由于 ,故 四点共面,B正确;
对于C:当 , 反向共线时, 也成立,但 与 夹角不为钝角,C错误;
对于D, 在 上的投影向量为 ,D正确.
故选:ABD.
11.ACD
【详解】对于A,三棱锥 的体积等于三棱锥 的体积,是定值,A正确;
以 为坐标原点, 分别为 轴,建立如图所示的空间直角坐标系,
则 ,设 ,则
对于B, ,使得 与 所成的角 满足:
,
因为 ,故 ,故 ,
而 ,B错误;
对于C,平面 的法向量 ,
所以直线 与平面 所成角 的正弦值为: ,
因为 ,故
故 ,
而 , ,
故 即 的取值范围为 ,C正确;对于D, ,由 ,
可得 ,化简可得 ,
在 平面内,令 ,得 ,令 ,得 ,则P的轨迹的长度为
,D正确;
故选:ACD.
12.
【详解】方程 表示圆
则
13.
【详解】结合空间直角坐标系中任意两点间的距离公式,
可得 表示的几何意义是空间内任意一点 与原点
及定点 ,的距离之和,
显然,当 三点共线且 在线段 上时, 最小,
最小值为 .
故答案为:
14.
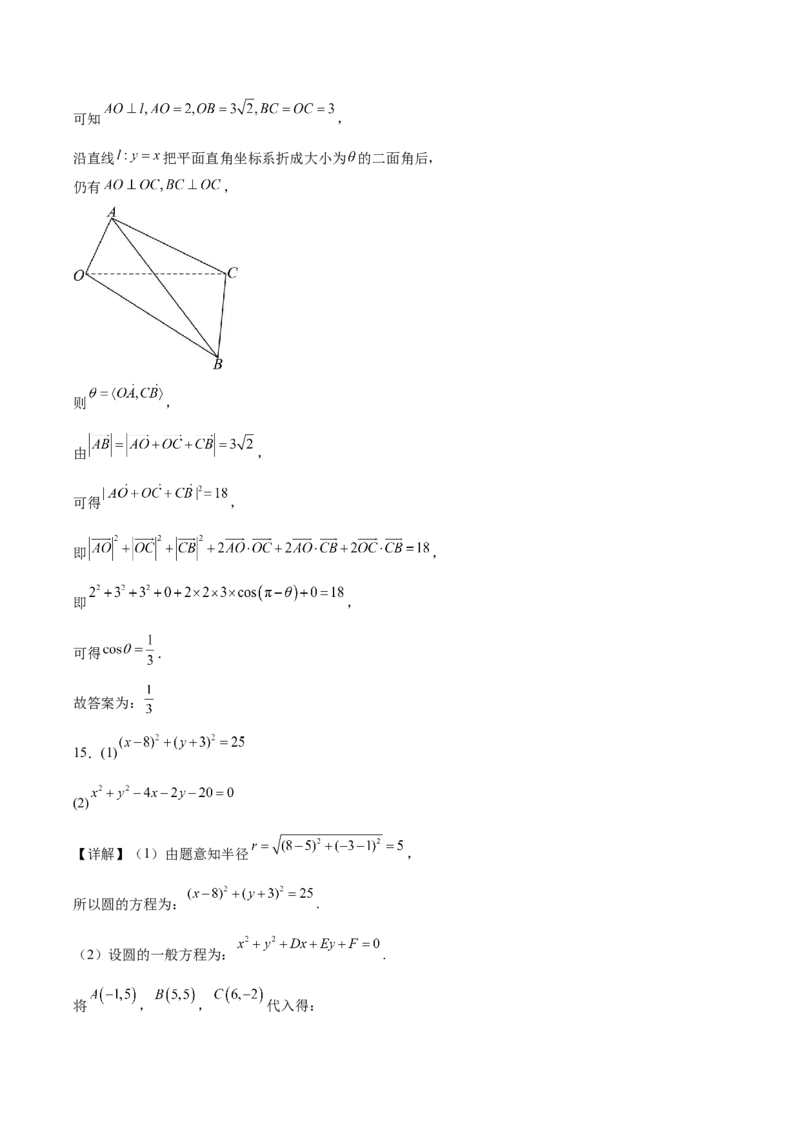
【详解】在平面直角坐标系中,过点 作 于点 ,可知 ,
沿直线 把平面直角坐标系折成大小为 的二面角后,
仍有 ,
则 ,
由 ,
可得 ,
即 ,
即 ,
可得 .
故答案为:
15.(1)
(2)
【详解】(1)由题意知半径 ,
所以圆的方程为: .
(2)设圆的一般方程为: .
将 , , 代入得:,
所以圆的方程为: .
16.(1)证明见解析
(2) .
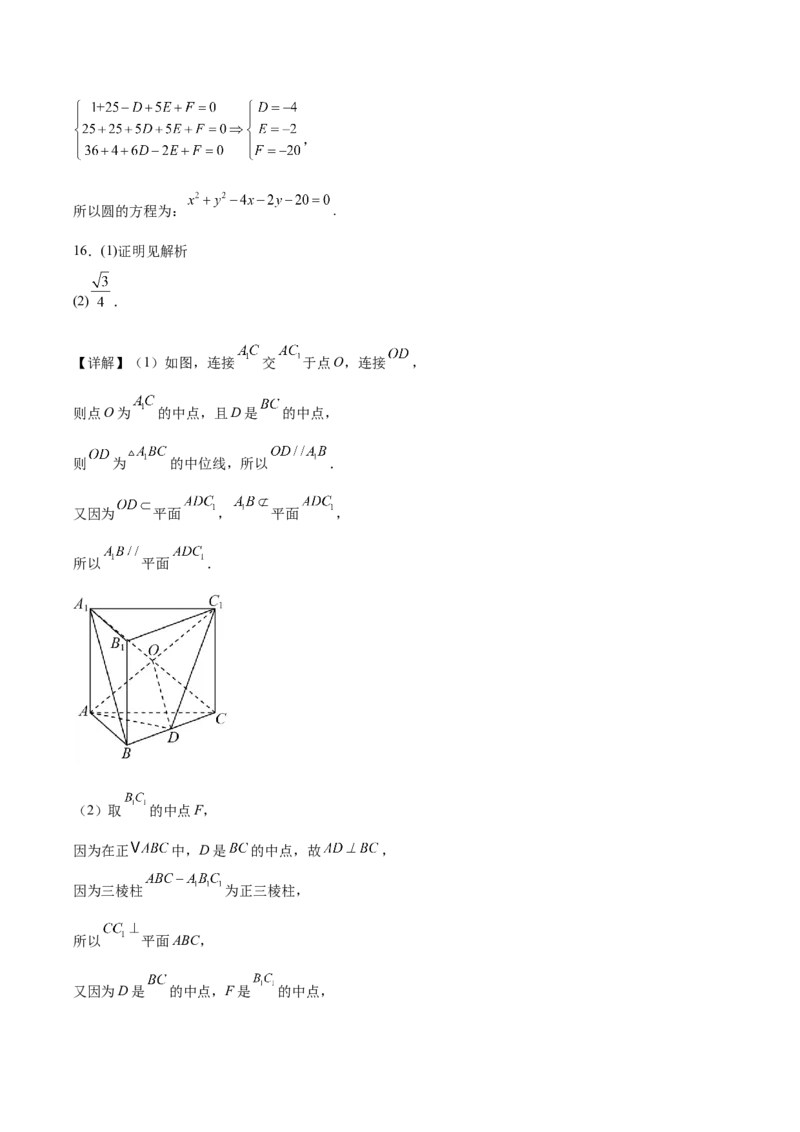
【详解】(1)如图,连接 交 于点O,连接 ,
则点O为 的中点,且D是 的中点,
则 为 的中位线,所以 .
又因为 平面 , 平面 ,
所以 平面 .
(2)取 的中点F,
因为在正 中,D是 的中点,故 ,
因为三棱柱 为正三棱柱,
所以 平面ABC,
又因为D是 的中点,F是 的中点,所以 ,
所以 平面 ,所以 , ,
以D为坐标原点,分别以 为 轴,建立空间直角坐标系,
则 , , , , , , .
故 , , ,
设平面 的法向量为 ,
则 ,令 ,则 ,即 .
设直线 与平面 所成角为 ,
可得 ,
所以直线 与平面 所成角的正弦值为 .
17.(1) ;
(2) ;
(3) .
【详解】(1) 的顶点 , , ,则对角线AC中点为 ,于是得对角线BD的中点是 ,设 ,因此有 , ,解得: ,
所以平行四边形ABCD的顶点 .
(2)因 , ,即有直线BC斜率 ,直线BC的方程: ,即
,
因此,点A到直线BC的距离为 ,而 ,
从而得 ,
所以四边形ABCD的面积为 .
(3)依题意,直线AB的斜率 ,则 边AB上的高所在直线的斜率为 ,
于是有: ,即 .
所以 边AB上的高所在直线的方程为 .
18.(1)
(2)存在,
【详解】(1)因为点 在底面ABC上的投影为AC的中点 ,所以 平面ABC,
又 平面ABC,故 , ,
因为 是以AC为斜边的等腰直角三角形,点 为AC的中点,故 ,
所以 , , 两两垂直,故以点 为坐标原点,直线 , , 分别为x,y,z轴,建立空
间直角坐标系,如图,.
因为 是以AC为斜边的等腰直角三角形, ,所以 , ,
因为侧面 为菱形,所以 ,
又 ,所以 ,
则 , , , , ,
则 , , ,
设平面 的一个法向量为 ,则 ,
取 ,则 ,故 ,
所以点 到平面 的距离为 .
(2)假设存在满足条件的点E,
则存在 ,使得 ,
则 ,
因为直线DE与侧面 所成角的正弦值为 ,
所以 ,即 ,解得 ,
又 ,故 ,
因此存在满足条件的点 ,且 ,即 .
19.(1)
(2)7
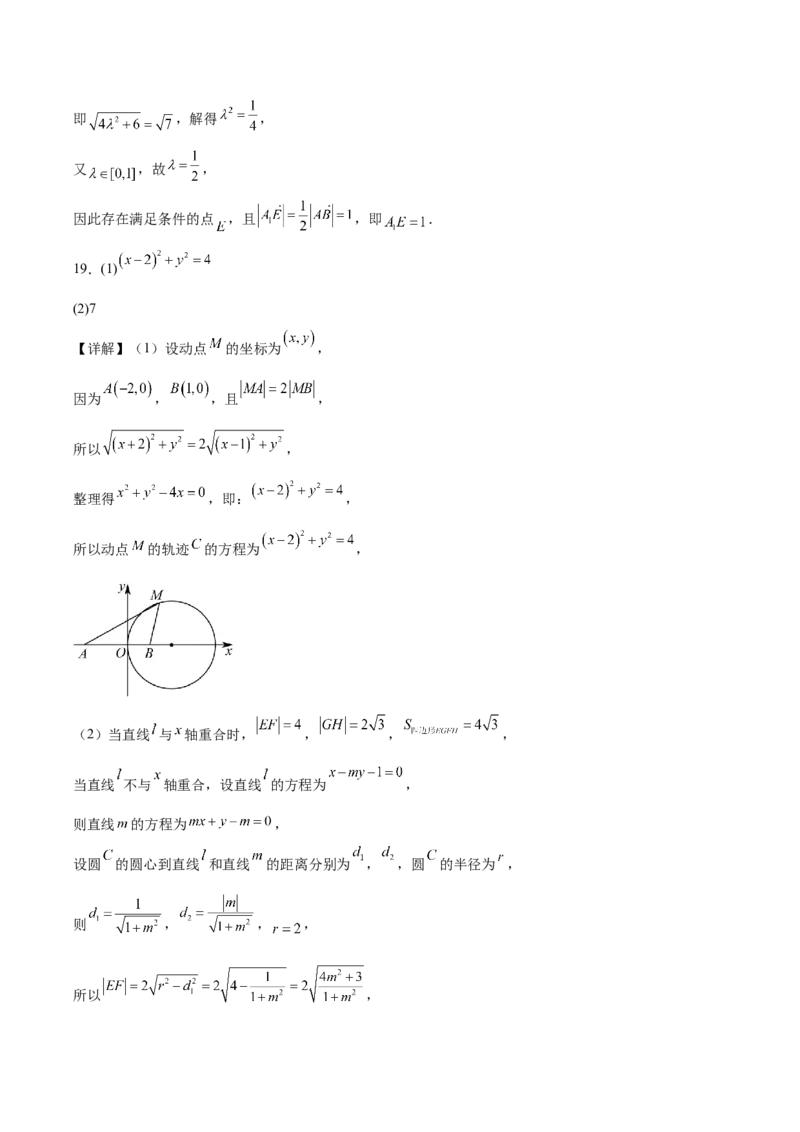
【详解】(1)设动点 的坐标为 ,
因为 , ,且 ,
所以 ,
整理得 ,即: ,
所以动点 的轨迹 的方程为 ,
(2)当直线 与 轴重合时, , , ,
当直线 不与 轴重合,设直线 的方程为 ,
则直线 的方程为 ,
设圆 的圆心到直线 和直线 的距离分别为 , ,圆 的半径为 ,
则 , , ,
所以 ,,
所以 ,
当 时, ,
当 时, ,
当且仅当 时等号成立,
综上所述,四边形 面积的最大值为7.