文档内容
嘉陵一中高 2024 级高二上第一次月考
数学试卷
注意事项: 时间120分钟,满分150分. 所有答案直接答在答题卡对应区域.
一、单选题:本题共8小题,每小题5分,共40分.在每小题给出的选项中,
只有一项是符合题目要求的.
1.在空间直角坐标系 中,与点 关于平面 对称的点为( )
A. B. C. D.
2.从分别写有1,2,3,4的4张卡片中不放回地随机抽取2张,则抽到的2张卡片上的
数字之和是奇数的概率为( )
A. B. C. D.
3.若直线 的一个方向向量为 ,平面 的一个法向量为 ,则可能使 的是
( )
A. B.
C. D.
4.设 ,则AB的中点M到点C的距离 (
)
A. B. C. D.
5.已知a=(1,2,-y),b=(x,1,2),且(a+2b)∥(2a-b),则( )
.
A x= ,y=1 B. x= ,y=-4 C. x=2,y=- D. x=1,y=-1
6.在平行六面体 中,底面 是边长为2的正方形,
学科网(北京)股份有限公司°,则异面直线 与 直线所成角的正弦值为( )
A. B. C. D.
7.已知二面角 , 、 两点在棱 上,直线 分别在这个二面角的两个半
平面内,且都垂直于 .已知 ,则二面角 的
大小是( )
A. 30° B. 60° C. 120° D. 150°
8.如图,在正四棱柱 中, , , 是侧面 内的
动点,且 ,记 与平面 所成的角为 ,则 的最大值为( )
A. B. C. 2 D.
二、多选题:本题共3小题,每小题6分,共18分.在每小题给出的四个选项
中,有多项符合题目要求.全部选对得6分,部分选对得部分分,选错得0分
9.设样本空间 含有等可能样本点,且 ,
则下列说法正确的是( )
A.事件 与 为互斥事件 B.事件 与 为对立事件
C.事件 两两相互独立 D.
10.下列说法不正确的是( )
A. 数据1,8,3,5,6的第60百分位数是5
学科网(北京)股份有限公司B. 若一组样本数据4,6,7,8,9, 的平均数为7,则
C. 用分层随机抽样时,个体数最多的层里的个体被抽到的概率最大
的
D. 若 标准差为4,则 的标准差是8
11.如图,在棱长为1的正方体 中,点O为线段 的中点,且点P满
足 ,则下列说法正确的是( )
A. 若 , ,则 B. 若 ,则 平面
C. 若 , ,则 平面
D. 若 , 时,直线 与平面 所成的角为 ,则
三、填空题:本题共3小题,每小题5分,共15分.
12.设异面直线 的方向向量分别为 ,则异面直线 所成角
的大小为 .
13.一个底面直径是32cm的圆柱形水桶装入一定量的水,将一个球放入桶内完全淹没,
水面上升了9cm且无溢出,则这个球的表面积是 .
14.点 是棱长为 的正四面体表面上的动点, 是该四面体内切球的一条直径,则
的最大值是 .
四、解答题:本题共5小题,共77分.其中15题13分, 16、17题15分,
18、19题17分.解答应写出文字说明,证明过程或演算步骤.
学科网(北京)股份有限公司15.(本题满分13分)已知空间中三点 , , ,设
, .
(1)已知向量 与 互相垂直,求 的值;
(2)若点 在平面 上,求 的值.
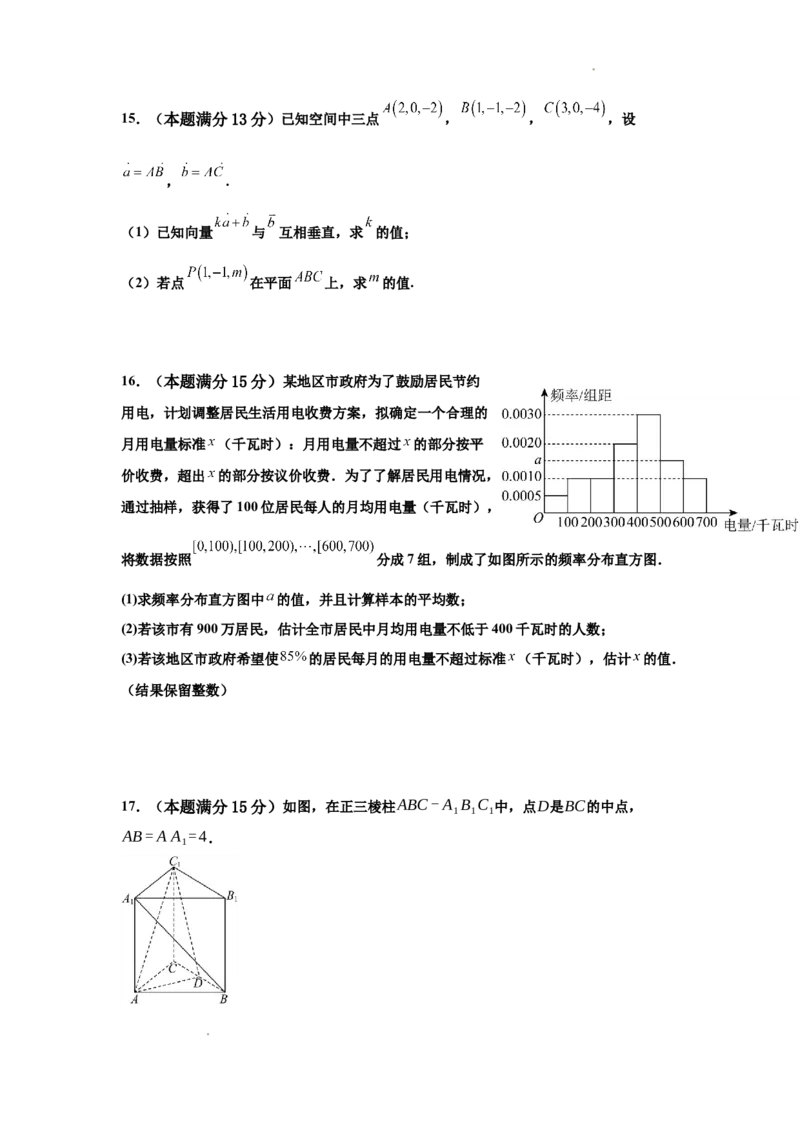
16.(本题满分15分)某地区市政府为了鼓励居民节约
用电,计划调整居民生活用电收费方案,拟确定一个合理的
月用电量标准 (千瓦时):月用电量不超过 的部分按平
价收费,超出 的部分按议价收费.为了了解居民用电情况,
通过抽样,获得了100位居民每人的月均用电量(千瓦时),
将数据按照 分成7组,制成了如图所示的频率分布直方图.
(1)求频率分布直方图中 的值,并且计算样本的平均数;
(2)若该市有900万居民,估计全市居民中月均用电量不低于400千瓦时的人数;
(3)若该地区市政府希望使 的居民每月的用电量不超过标准 (千瓦时),估计 的值.
(结果保留整数)
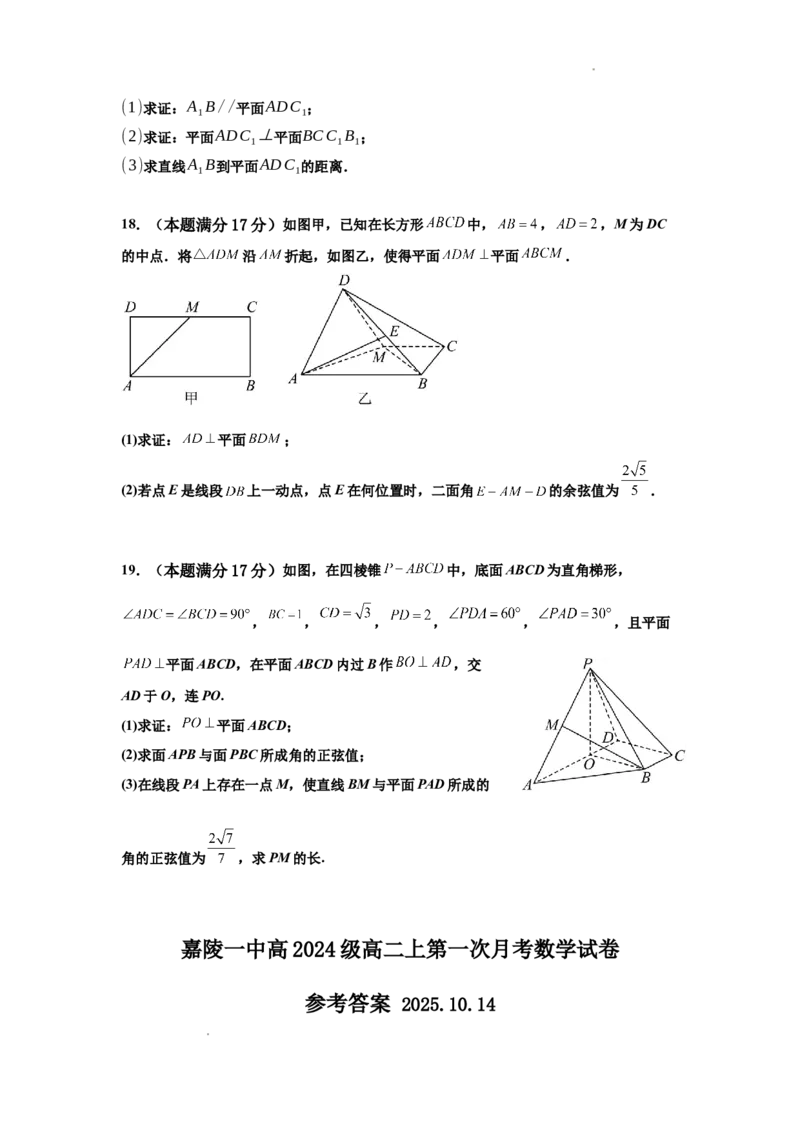
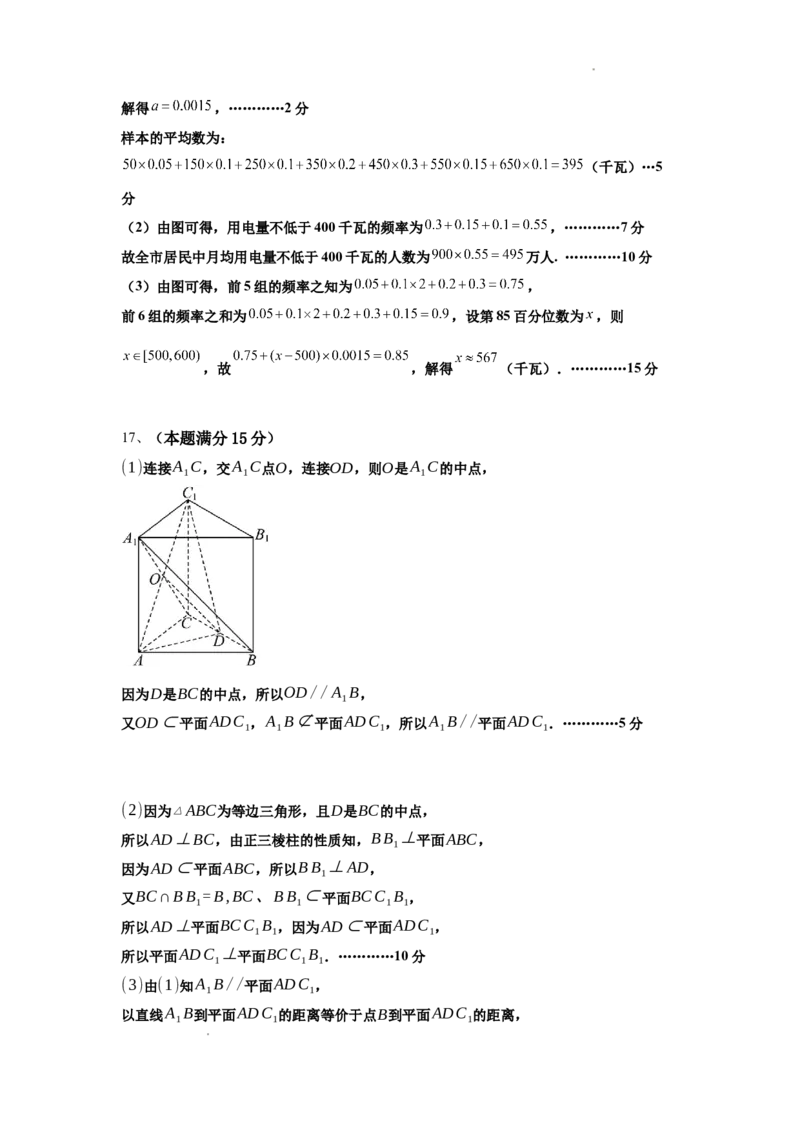
17.(本题满分15分)如图,在正三棱柱ABC-A B C 中,点D是BC的中点,
1 1 1
AB=A A =4.
1
学科网(北京)股份有限公司(1)求证:A B//平面ADC ;
1 1
(2)求证:平面ADC ⊥平面BCC B ;
1 1 1
(3)求直线A B到平面ADC 的距离.
1 1
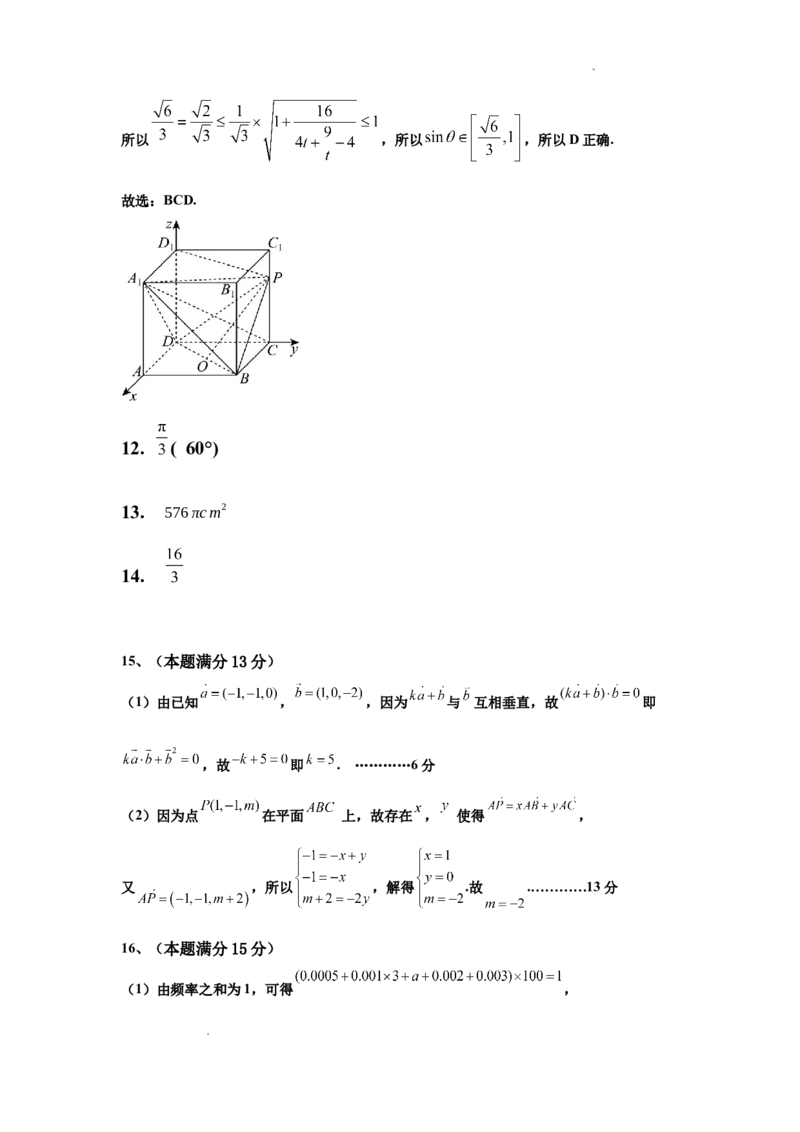
18.(本题满分17分)如图甲,已知在长方形 中, , ,M为DC
的中点.将 沿 折起,如图乙,使得平面 平面 .
(1)求证: 平面 ;
(2)若点E是线段 上一动点,点E在何位置时,二面角 的余弦值为 .
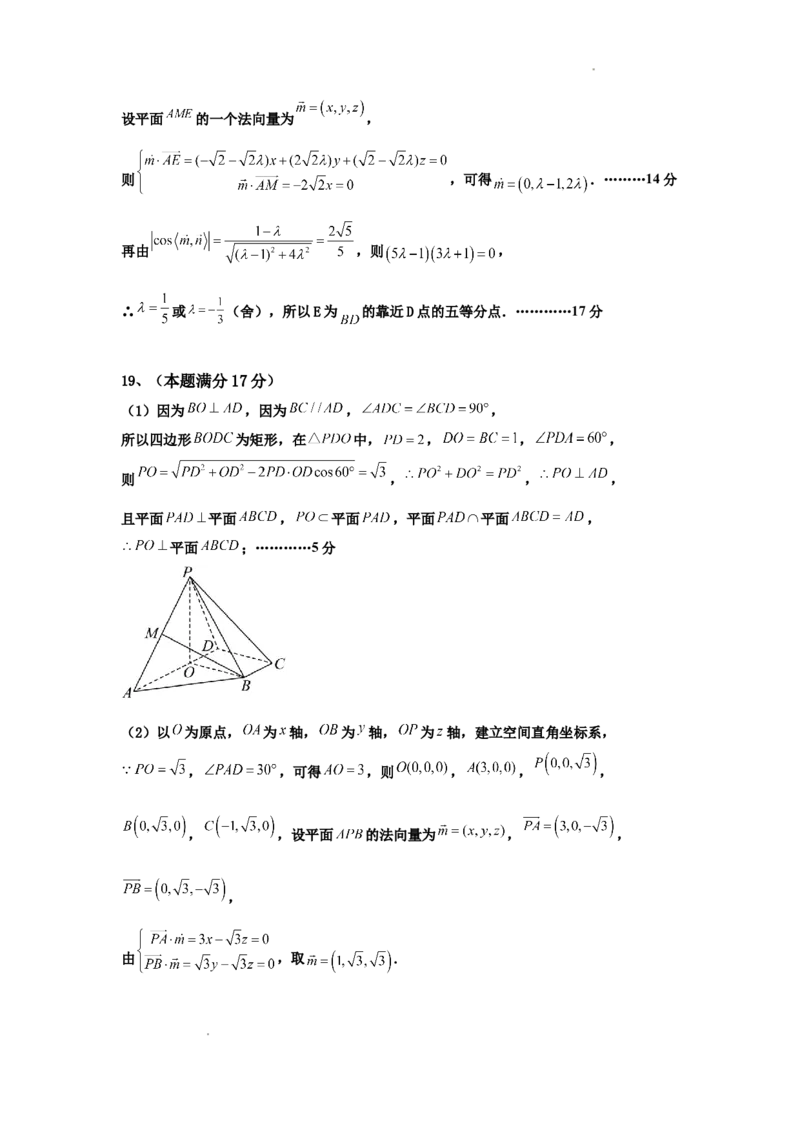
19.(本题满分17分)如图,在四棱锥 中,底面ABCD为直角梯形,
, , , , , ,且平面
平面ABCD,在平面ABCD内过B作 ,交
AD于O,连PO.
(1)求证: 平面ABCD;
(2)求面APB与面PBC所成角的正弦值;
(3)在线段PA上存在一点M,使直线BM与平面PAD所成的
角的正弦值为 ,求PM的长.
嘉陵一中高 2024 级高二上第一次月考数学试卷
参考答案 2025.10.14
学科网(北京)股份有限公司1-4ADCD 5-8BACB
8【分析】以 , , 所在直线分别为 , , 轴,建立空间直角坐标系,
设 ,3, ,根据空间向量垂直的坐标表示求得 ,继而得 的最小值,
连接BP,由线面角的定义得 就是 与平面 所成的角,故而得
的最大值.
解:以 , , 所在直线分别为 , , 轴,建立空间直角坐标系,则
, ,
设 ,3, ,则 ,3, , , , ,
, ,
, ,
,
连接BP,在正四棱柱 中, 面 ,所以 就是
与平面 所成的角,即 ,
, 的最大值为 .
故选:B.
9.BC 10. ABC 11. BCD
学科网(北京)股份有限公司11.连接 , , , , ,以D为原点,建立如图所示空间直角坐标系,
如图所示,可得 , , , , ,
则 ,
即 ,
对于A中,若 ,则 ,则P点与C点重合,
可得 ,所以A错误;
对于B中,若 ,则 , , ,
,
设平面 的法向量为 ,则 ,
取 ,可得 ,所以 ,
由于 ,可得 ,
因为 平面 ,所以 平面 ,所以B正确;
对于C中,若 ,则 , ,
由于 ,所以 平面 ,所以C正确;
学科网(北京)股份有限公司对于D中,若 时,可得 ,所以 ,
则
,
设 , ,则 , , ,
则 ,
由于函数 ( )在 上单调递减,在 上单调递增,
且 , , ,
所以 ,所以 , ,
, , ,
学科网(北京)股份有限公司所以 ,所以 ,所以D正确.
故选:BCD.
12. ( 60°)
13. 576πcm2
14.
15、(本题满分13分)
(1)由已知 , ,因为 与 互相垂直,故 即
,故 即 . …………6分
(2)因为点 在平面 上,故存在 , 使得 ,
又 ,所以 ,解得 .故 .…………13分
16、(本题满分15分)
(1)由频率之和为1,可得 ,
学科网(北京)股份有限公司解得 ,…………2分
样本的平均数为:
(千瓦)…5
分
(2)由图可得,用电量不低于400千瓦的频率为 ,…………7分
故全市居民中月均用电量不低于400千瓦的人数为 万人. …………10分
(3)由图可得,前5组的频率之知为 ,
前6组的频率之和为 ,设第85百分位数为 ,则
,故 ,解得 (千瓦).…………15分
17、(本题满分15分)
(1)连接A C,交A C点O,连接OD,则O是A C的中点,
1 1 1
因为D是BC的中点,所以OD//A B,
1
又OD⊂平面ADC ,A B⊄平面ADC ,所以A B//平面ADC .…………5分
1 1 1 1 1
(2)因为▵ABC为等边三角形,且D是BC的中点,
所以AD⊥BC,由正三棱柱的性质知,BB ⊥平面ABC,
1
因为AD⊂平面ABC,所以BB ⊥AD,
1
又BC∩BB =B,BC、BB ⊂平面BCC B ,
1 1 1 1
所以AD⊥平面BCC B ,因为AD⊂平面ADC ,
1 1 1
所以平面ADC ⊥平面BCC B .…………10分
1 1 1
(3)由(1)知A B//平面ADC ,
1 1
以直线A B到平面ADC 的距离等价于点B到平面ADC 的距离,
1 1 1
学科网(北京)股份有限公司由(2)知AD⊥平面BCC B ,所以点A到平面BDC 的距离为AD,
1 1 1
1 1
而S = AD⋅DC = ×2√3×√42+22=2√15,
▵ADC 1 2 1 2
1 1
S = BD⋅CC = ×2×4=4,
▵BDC 1 2 1 2
设点B到平面ADC 的距离为d,
1
因为V =V ,
B-ADC A-BDC
1 1
1 1 1 1 4√5
所以 ⋅d⋅S = ⋅AD⋅S ,即 ⋅d⋅2√15= ⋅2√3⋅4,解得d= ,
3 ▵ADC 1 3 ▵BDC 1 3 3 5
4√5
所以直线A B到平面ADC 的距离为 .…………15分
1 1 5
注:用空间向量法计算正确得相应分
18、(本题满分17分)
【详解】(1)证明:∵ ,∴ ,
∵ ,∴ ,∵ ,∴ ,∴ ,
∵平面 平面 ,平面 平面 , 平面 ,
∴ 平面 ,∵ 平面 ,∴ ,
∵ 且 , , 平面 ,∴ 平面 .……7分
(2)因为平面 平面 , , ,M是 的中点,
∴ ,取 的中点O,连接 ,则 平面 ,
取 的中点N,连接 ,则 ,以O为原点,建立如图所示的空间直角坐标系.
则 , , , ,…………9分
设 , ,因为平面 的一个法向量 ,…………11分
, ,
学科网(北京)股份有限公司设平面 的一个法向量为 ,
则 ,可得 .………14分
再由 ,则 ,
∴ 或 (舍),所以E为 的靠近D点的五等分点.…………17分
19、(本题满分17分)
(1)因为 ,因为 , ,
所以四边形 为矩形,在 中, , , ,
则 , , ,
且平面 平面 , 平面 ,平面 平面 ,
平面 ;…………5分
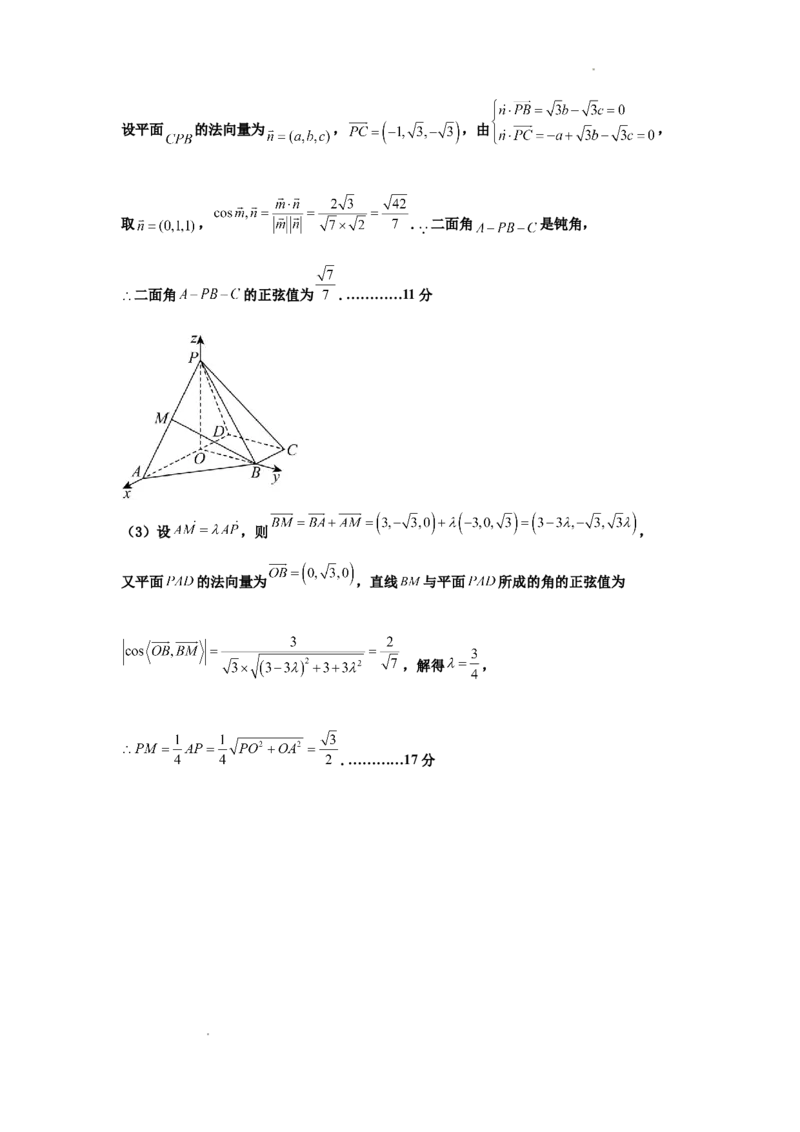
(2)以 为原点, 为 轴, 为 轴, 为 轴,建立空间直角坐标系,
, ,可得 ,则 , , ,
, ,设平面 的法向量为 , ,
,
由 ,取 .
学科网(北京)股份有限公司设平面 的法向量为 , ,由 ,
取 , . 二面角 是钝角,
二面角 的正弦值为 .…………11分
(3)设 ,则 ,
又平面 的法向量为 ,直线 与平面 所成的角的正弦值为
,解得 ,
.…………17分
学科网(北京)股份有限公司