2005年四川高考文科数学真题及答案_数学高考真题试卷_旧1990-2007·高考数学真题_1990-2007·高考数学真题·PDF_四川

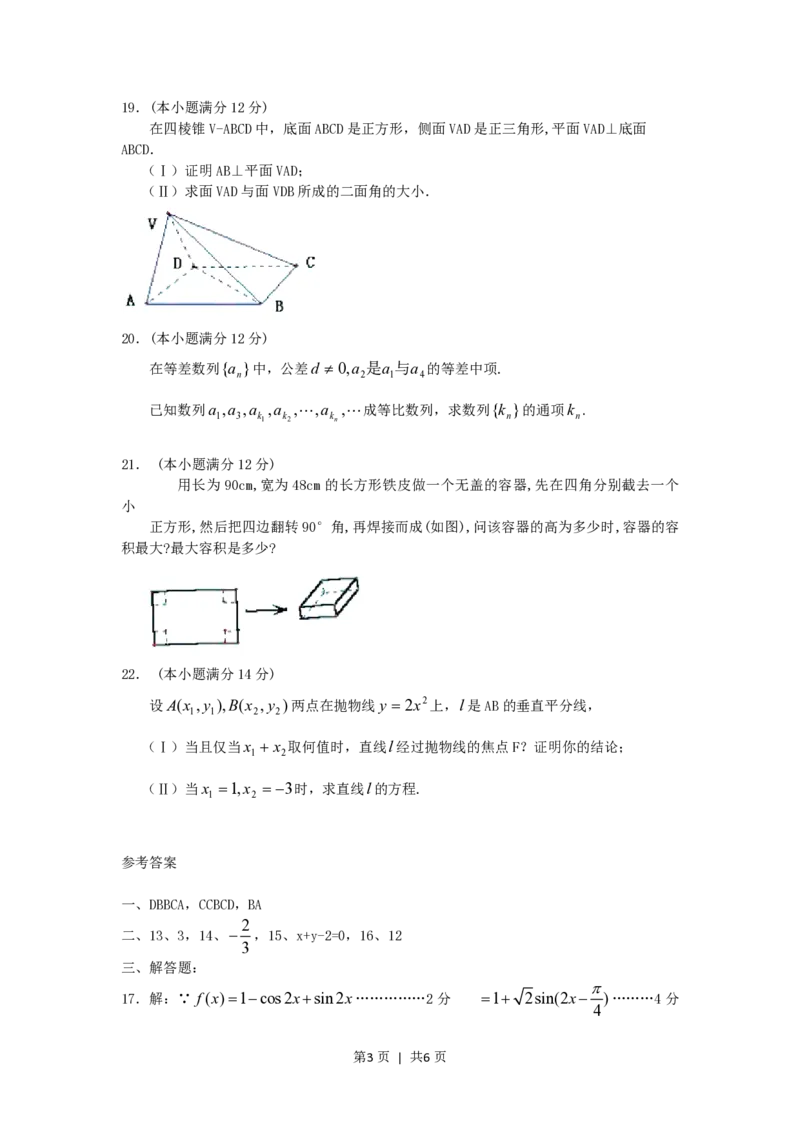
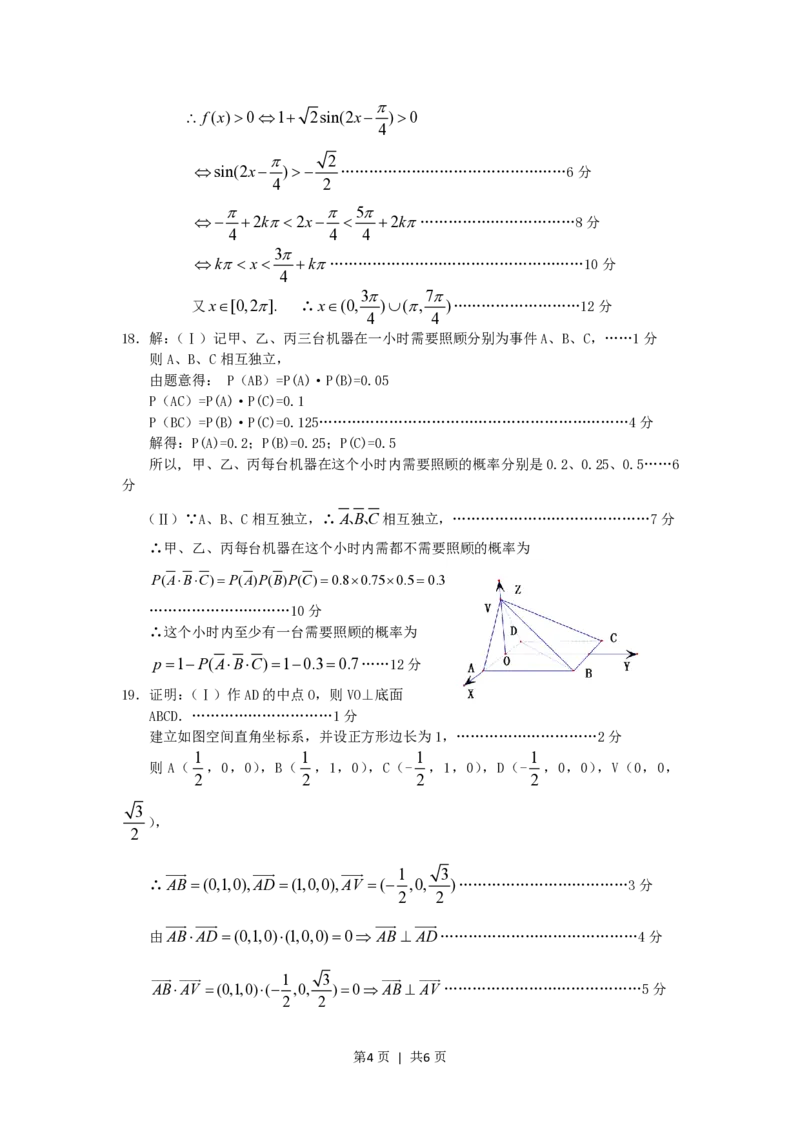
2005 年四川高考文科数学真题及答案 本试卷分第I卷（选择题）和第II卷（非选择题）两部分. 共150分. 考试时间120分钟. 第I卷 参考公式： 球的表面积公式 如果事件A、B互斥，那么 S=4R2 P（A+B）=P(A)+P(B) 其中R表示球的半径， 如果事件A、B相互独立，那么 球的体积公式 P（A·B）=P(A)·P(B) 4 V= R3， 如果事件A在一次试验中发生的概率是P，那么 3 n次独立重复试验中恰好发生k次的概率 其中R表示球的半径 P(k)=CkPk(1－P)n－k n n 一、选择题：每小题5分，共60分.  1．已知为第三象限角，则 所在的象限是 （ ） 2 A．第一或第二象限 B．第二或第三象限 C．第一或第三象限 D．第二或第四象限 2．已知过点A(－2，m)和B(m，4)的直线与直线2x+y-1=0平行，则m的值为 （ ） A．0 B．－8 C．2 D．10 3．在(x1)(x1)8的展开式中x5的系数是 （ ） A．－14 B．14 C．－28 D．28 4．设三棱柱ABC-ABC 的体积为V，P、Q分别是侧棱AA、CC 上的点，且PA=QC，则四棱 1 1 1 1 1 1 锥B-APQC的体积为 （ ） 1 1 1 1 A． V B． V C． V D． V 6 4 3 2 1 5．设3x  ，则 （ ） 7 A．－20, 1036时，V′>0, 所以,当x=10,V有极大值V(10)=1960………………………………………10分 又V(0)=0,V(24)=0,………………………………………………………………11分 所以当x=10,V有最大值V(10)=1960……………………………………………12分 y 1 22．解：（Ⅰ）∵抛物线y  2x2，即x2  ,p  ， 2 4 1 ∴焦点为F(0, )………………………………………………………1分 8 （1）直线l的斜率不存在时，显然有x  x 0………………………………3分 1 2 （2）直线l的斜率存在时，设为k， 截距为b 第5页 | 共6页即直线l：y=kx+b 由已知得： y  y x x  1 2 k 1 2b 2x22x2 x x  2 2 ……………5分  1 2k 1 2b   2 2    y x 1 1  x y 2 2  1 k     2x x 1 1 2  2 x 2 x2 2 1 k  x x   x 1 2x2 2 k 1 2 2b ……………7分 x2x2 1 b0b 1  1 2 4 4  x x  1  1 2 2k 1 即l的斜率存在时，不可能经过焦点F(0, )……………………………………8分 8 所以当且仅当x x =0时，直线l经过抛物线的焦点F…………………………9分 1 2 （Ⅱ）当x 1,x 3时， 1 2 直线l的斜率显然存在，设为l：y=kx+b………………………………10分 则由（Ⅰ）得：  x x  x x    x 1 2x2 2 k 1 2 2b     k 1 2 2b10 ………………………11分  x x  1   1 2  1 2 2k  2k  1 k   4 …………………………………………13分  41 b  4 1 41 所以直线l的方程为y  x ，即x4y410………………14分 4 4 第6页 | 共6页