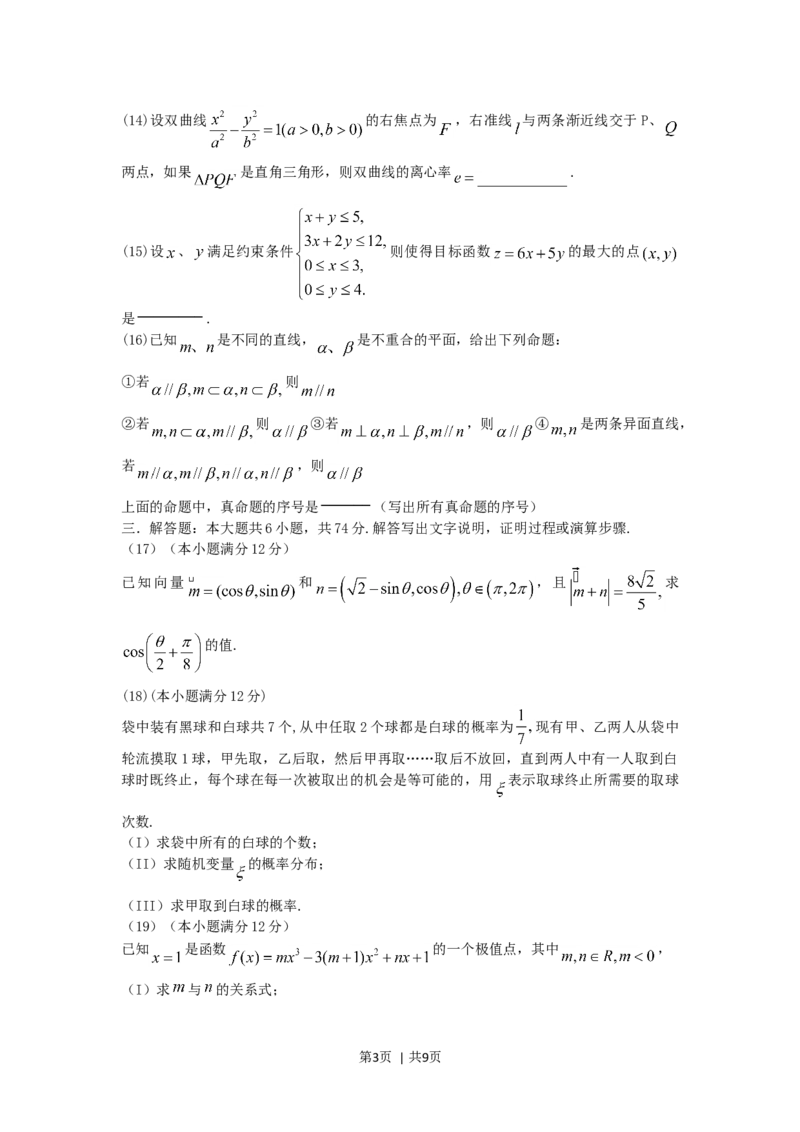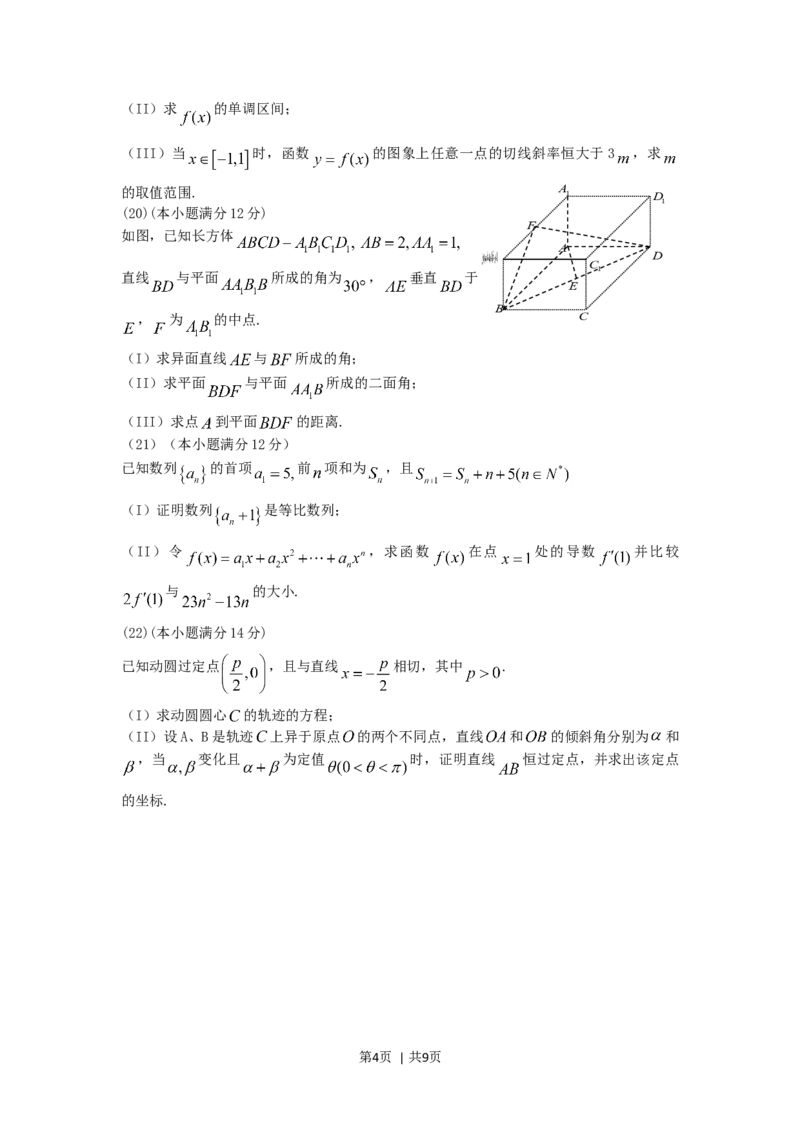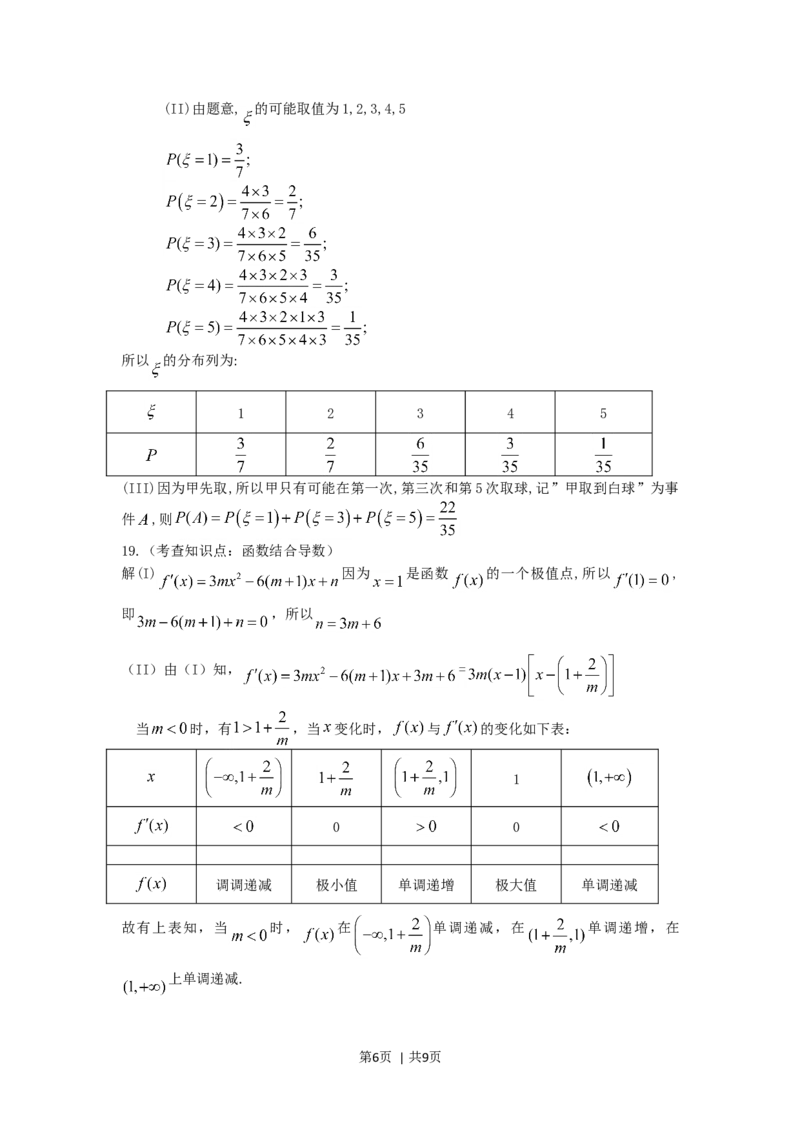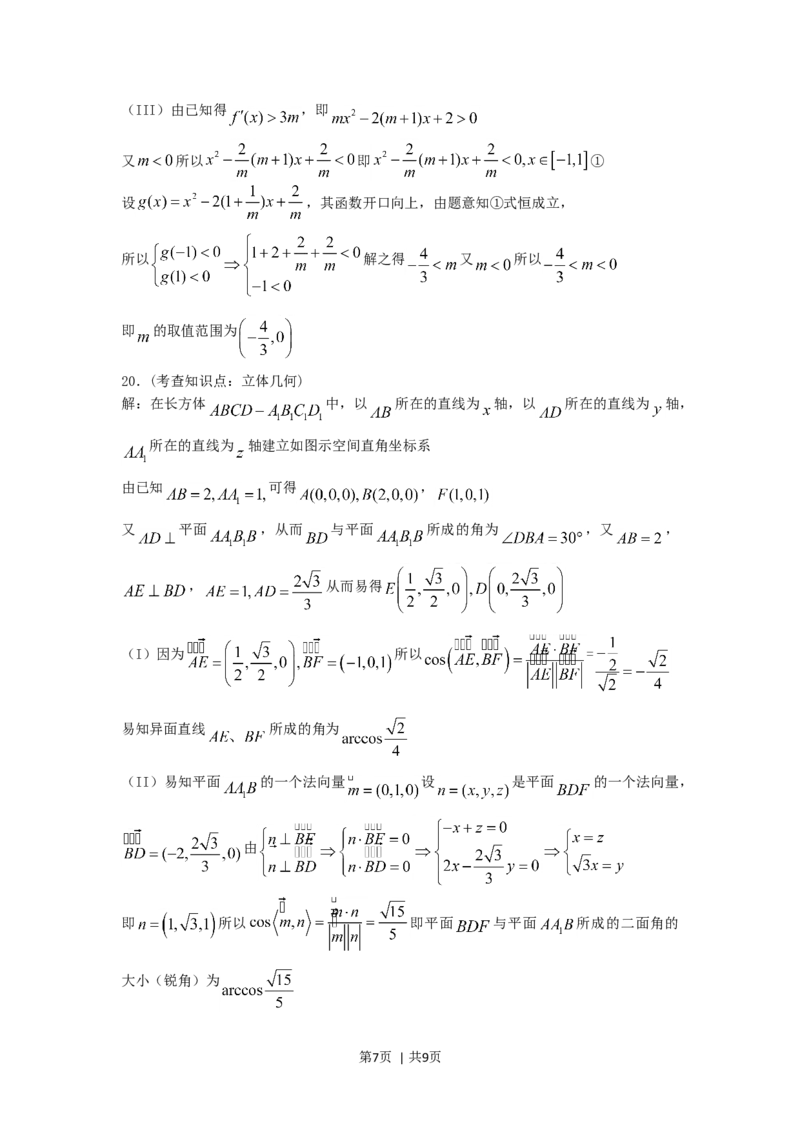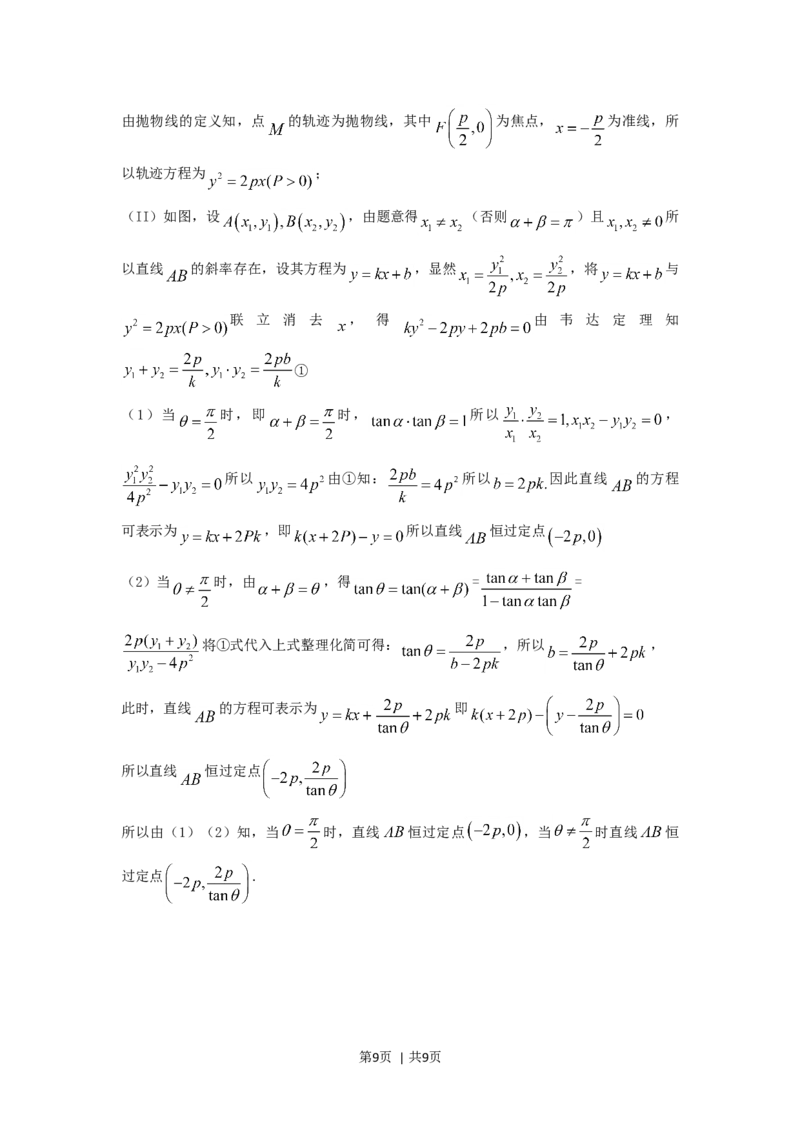2005年山东高考理科数学真题及答案_数学高考真题试卷_旧1990-2007·高考数学真题_1990-2007·高考数学真题·word_山东

2005 年山东高考理科数学真题及答案 第I卷（共60分） 参考公式：如果事件A、B互斥，那么 如果事件A、B相互独立，那么 一．选择题：本大题共12小题，每题5分，共60分，在每小题给出的四个选项中，选择 一个符合题目要求的选项. （1） （ ） （A） （B） （C）1 （D） （2）函数 的反函数图像大致是 （ ） y y y y （A） （B） （C） （D） 1 1 1 1 o x o x o x o x （3）已知函数 ，则下列判断正确的是（ ） （A）此函数的最小周期为 ，其图像的一个对称中心是 （B）此函数的最小周期为 ，其图像的一个对称中心是 （C）此函数的最小周期为 ，其图像的一个对称中心是 （D）此函数的最小周期为 ，其图像的一个对称中心是 （4）下列函数既是奇函数，又在区间 上单调递减的是（ ） （ A ） （ B ） （ C ） （ D ） 第1页 | 共9页（5）如果 的展开式中各项系数之和为128，则展开式中 的系数是（ ） （A）7 （B） （C）21 （D） （6）函数 ，若 则 的所有可能值为（ ） （A）1 （B） （C） （D） （7）已知向量 ，且 ， ，则一定共线的三 点是（ ） （ A）A、B、D （B）A、B、C （C）B、C、D （D）A、C、D （8）设地球的半径为 ，若甲地位于北纬 东经 ，乙地位于南纬 东经 ， 则甲、乙两地的球面距离为（ ） （A） （B） （C） （D） （9）10张奖券中只有3张有奖，5个人购买，至少有1人中奖的概率是（ ） （A） （B） （C） （D） （10）设集合A、B是全集 的两个子集，则 是 的（ ） （A）充分不必要条件（B）必要不充分条件（C）冲要条件（D）既不充分也不必要条件 （11） ，下列不等式一定成立的是（ ） （A） （B） （C） （D） （12）设直线 关于原点对称的直线为 ，若 与椭圆 的交点 为A、B、，点 为椭圆上的动点，则使 的面积为 的点 的个数为（ ） （A）1 （B）2 （C）3 （D）4 第II卷（共90分） 二．填空题：本大题共4小题，每小题4分，共16分.答案须填在题中横线上. （13） . 第2页 | 共9页(14)设双曲线 的右焦点为 ，右准线 与两条渐近线交于P、 两点，如果 是直角三角形，则双曲线的离心率 . (15)设 、 满足约束条件 则使得目标函数 的最大的点 是 . (16)已知 是不同的直线， 是不重合的平面，给出下列命题： ①若 则 ②若 则 ③若 ，则 ④ 是两条异面直线， 若 ，则 上面的命题中，真命题的序号是 （写出所有真命题的序号） 三．解答题：本大题共6小题，共74分.解答写出文字说明，证明过程或演算步骤. （17）（本小题满分12分） 已知向量 和 ，且 求 的值. (18)(本小题满分12分) 袋中装有黑球和白球共7个,从中任取2个球都是白球的概率为 现有甲、乙两人从袋中 轮流摸取1球，甲先取，乙后取，然后甲再取……取后不放回，直到两人中有一人取到白 球时既终止，每个球在每一次被取出的机会是等可能的，用 表示取球终止所需要的取球 次数. （I）求袋中所有的白球的个数； （II）求随机变量 的概率分布； （III）求甲取到白球的概率. （19）（本小题满分12分） 已知 是函数 的一个极值点，其中 ， （I）求 与 的关系式； 第3页 | 共9页（II）求 的单调区间； （III）当 时，函数 的图象上任意一点的切线斜率恒大于3 ，求 的取值范围. A 1 D 1 (20)(本小题满分12分) F 如图，已知长方体 A f(x)mx33(m1)x2nx1 D C 1 直线 与平面 所成的角为 ， 垂直 于 E B ， 为 的中点. C （I）求异面直线 与 所成的角； （II）求平面 与平面 所成的二面角； （III）求点 到平面 的距离. （21）（本小题满分12分） 已知数列 的首项 前 项和为 ，且 （I）证明数列 是等比数列； （II）令 ，求函数 在点 处的导数 并比较 与 的大小. 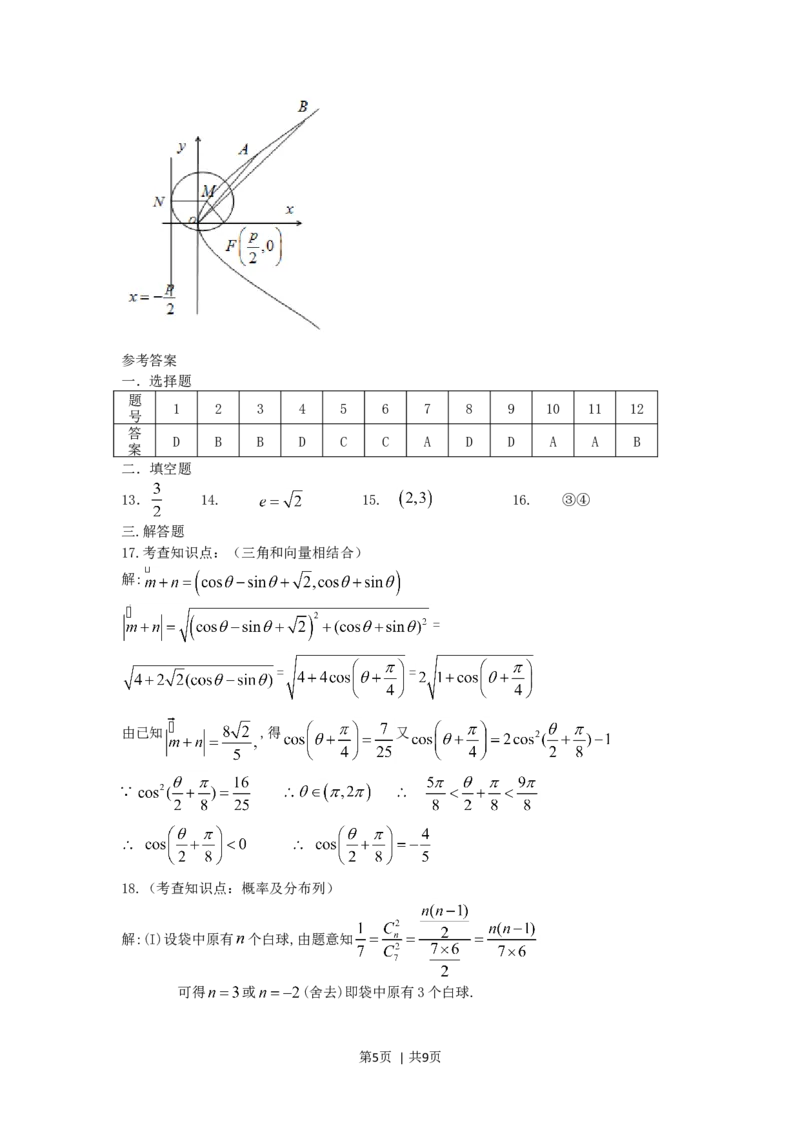(22)(本小题满分14分) 已知动圆过定点 ，且与直线 相切，其中 . （I）求动圆圆心 的轨迹的方程； （II）设A、B是轨迹 上异于原点 的两个不同点，直线 和 的倾斜角分别为 和 ，当 变化且 为定值 时，证明直线 恒过定点，并求出该定点 的坐标. 第4页 | 共9页参考答案 一．选择题 题 1 2 3 4 5 6 7 8 9 10 11 12 号 答 D B B D C C A D D A A B 案 二．填空题 13． 14. 15. 16. ③④ 三.解答题 17.考查知识点：（三角和向量相结合） 解: = = = 由已知 ,得 又 18.（考查知识点：概率及分布列） 解:(I)设袋中原有 个白球,由题意知 可得 或 (舍去)即袋中原有3个白球. 第5页 | 共9页(II)由题意, 的可能取值为1,2,3,4,5 所以 的分布列为: 1 2 3 4 5 (III)因为甲先取,所以甲只有可能在第一次,第三次和第5次取球,记”甲取到白球”为事 件 ,则 19.（考查知识点：函数结合导数） 解(I) 因为 是函数 的一个极值点,所以 , 即 ，所以 （II）由（I）知， = 当 时，有 ，当 变化时， 与 的变化如下表： 1 0 0 调调递减 极小值 单调递增 极大值 单调递减 故有上表知，当 时， 在 单调递减，在 单调递增，在 上单调递减. 第6页 | 共9页（III）由已知得 ，即 又 所以 即 ① 设 ，其函数开口向上，由题意知①式恒成立， 所以 解之得 又 所以 即 的取值范围为 20．(考查知识点：立体几何) 解：在长方体 中，以 所在的直线为 轴，以 所在的直线为 轴， 所在的直线为 轴建立如图示空间直角坐标系 由已知 可得 ， 又 平面 ，从而 与平面 所成的角为 ，又 ， ， 从而易得 （I）因为 所以 = 易知异面直线 所成的角为 （II）易知平面 的一个法向量 设 是平面 的一个法向量， 由 即 所以 即平面 与平面 所成的二面角的 大小（锐角）为 第7页 | 共9页（III）点 到平面 的距离，即 在平面 的法向量 上的投影的绝对值， 所以距离 = 所以点 到平面 的距离为 21．（考查知识点:数列） 解：由已知 可得 两式相减得 即 从 而 当 时 所以 又 所以 从而 故总有 ， 又 从而 即数列 是 等比数列； （II）由（I）知 因为 所以 从而 = = - = 由上 - = =12 ① 当 时，①式=0所以 ； 当 时，①式=-12 所以 当 时， 又 所以 即① 从而 22．（考查知识点:圆锥曲线） 解：（I）如图，设 为动圆圆心， 为记为 ，过点 作直线 的垂线， 垂足为 ，由题意知： 即动点 到定点 与定直线 的距离相等， 第8页 | 共9页由抛物线的定义知，点 的轨迹为抛物线，其中 为焦点， 为准线，所 以轨迹方程为 ； （II）如图，设 ，由题意得 （否则 ）且 所 以直线 的斜率存在，设其方程为 ，显然 ，将 与 联 立 消 去 ， 得 由 韦 达 定 理 知 ① （1）当 时，即 时， 所以 ， 所以 由①知： 所以 因此直线 的方程 可表示为 ，即 所以直线 恒过定点 （2）当 时，由 ，得 = = 将①式代入上式整理化简可得： ，所以 ， 此时，直线 的方程可表示为 即 所以直线 恒过定点 所以由（1）（2）知，当 时，直线 恒过定点 ，当 时直线 恒 过定点 . 第9页 | 共9页