文档内容
数学(二) 参考答案
一、选择题
1~8. BCBA CCAD
8题提示: 对 取对数, , , ,考察
函数 ,则 所以
为增函数, , 所以 ,所以
二、选择题
9. ACD 10. AD 11. ABC 12. AD
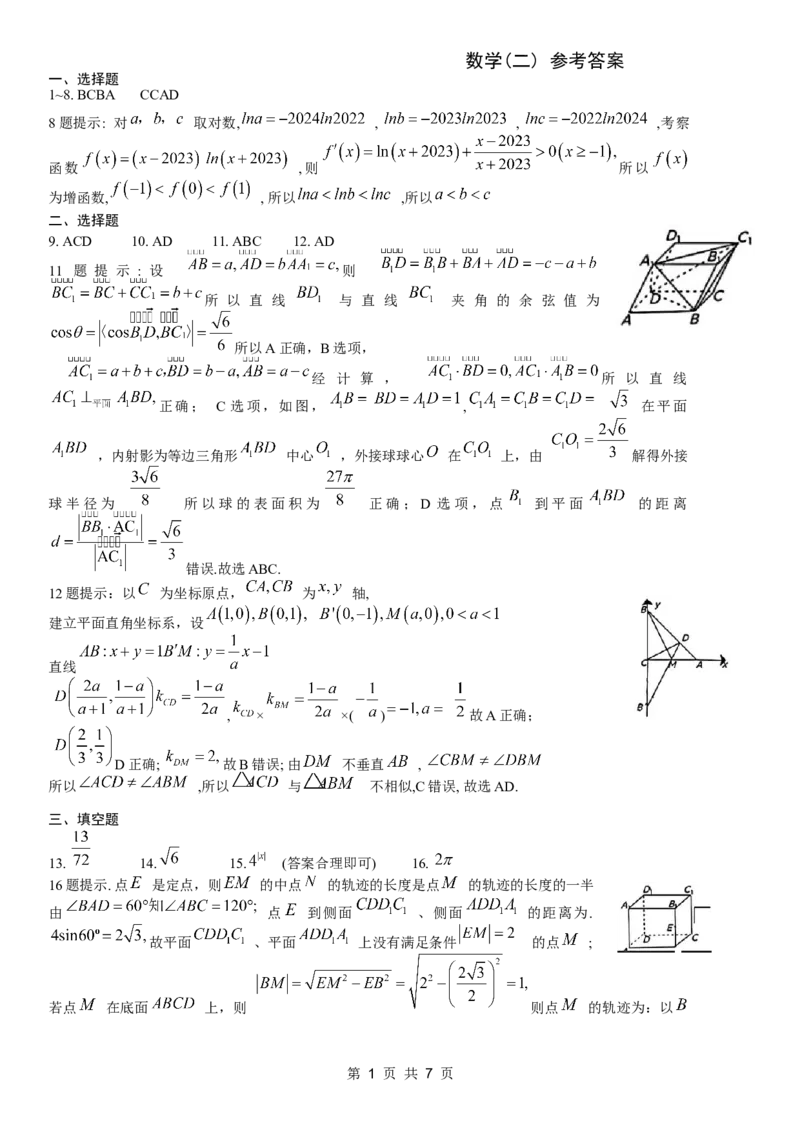
11 题 提 示 : 设 则
所 以 直 线 与 直 线 夹 角 的 余 弦 值 为
所以A正确,B选项,
经 计 算 , 所 以 直 线
正确; C 选项,如图, , 在平面
,内射影为等边三角形 中心 ,外接球球心 在 上,由 解得外接
球半径为 所以球的表面积为 正确;D 选项,点 到平面 的距离
错误.故选ABC.
12题提示:以 为坐标原点, 为 轴,
建立平面直角坐标系,设
直线
, × ×( ) 故A正确;
D正确; 故B错误; 由 不垂直 ,
所以 ,所以 与 不相似,C错误, 故选AD.
三、填空题
13. 14. 15. (答案合理即可) 16.
16题提示. 点 是定点,则 的中点 的轨迹的长度是点 的轨迹的长度的一半
由 点 到侧面 、侧面 的距离为.
故平面 、平面 上没有满足条件 的点 ;
若点 在底面 上,则 则点 的轨迹为:以
第 1 页 共 7 页为圆心,半径 的 圆,轨迹长度为 同理: 若点 在底面 上时, 轨迹
长度也为 若点 在侧面 上,则点 的轨迹为: 以 为圆心,半径 的 圆,
轨迹长度为
同理:若点 在侧面 上时,轨迹长度也为
综上所述:点 的轨迹的长度为 故点 的轨迹的长度 .
四、解答题
17.(10分)
,所以 ,即 ;…………………(2 分)因为
解: (1) 因为
,所以 ,故 ,故 ………(4分)由
知
结合 知 …………(6分)
(2) 记 的中点为 ,设
在△ABD 中, 由余弦定理:
解得: ;………………(8分)
所以
所以△ABC 的面积为 …………(10分)
18. (12分)
解:(1)列联表:…………………………………………………………………………………(2分)
篮球迷 非篮球迷 总计
男生 36 24 60
女生 16 24 40
总计 52 48 100
提出零假设 :是否为“篮球迷”与性别无关联;
则 ……………(5分)
依据小概率值 的独立性检验,没有充分证据认为零假设 不成立;则 成立,故没有把
握认为是否为“篮球迷”与性别有关联……………………………………………………(6分)
(2)根据按比例的分层抽样:抽取的“篮球迷”人数为3人,“非篮球迷”人数为2人;……………(7分)
记“恰有两人闯关成功”为事件A、“有“篮球迷”闯关成功”为事件B;
则 …………(9分)
第 2 页 共 7 页;…………………………(11分)
由条件概率的公式得
故在恰有两人闯关成功的条件下,有“篮球迷”闯关成功的概率为 ……………(12分)
19. (12分)
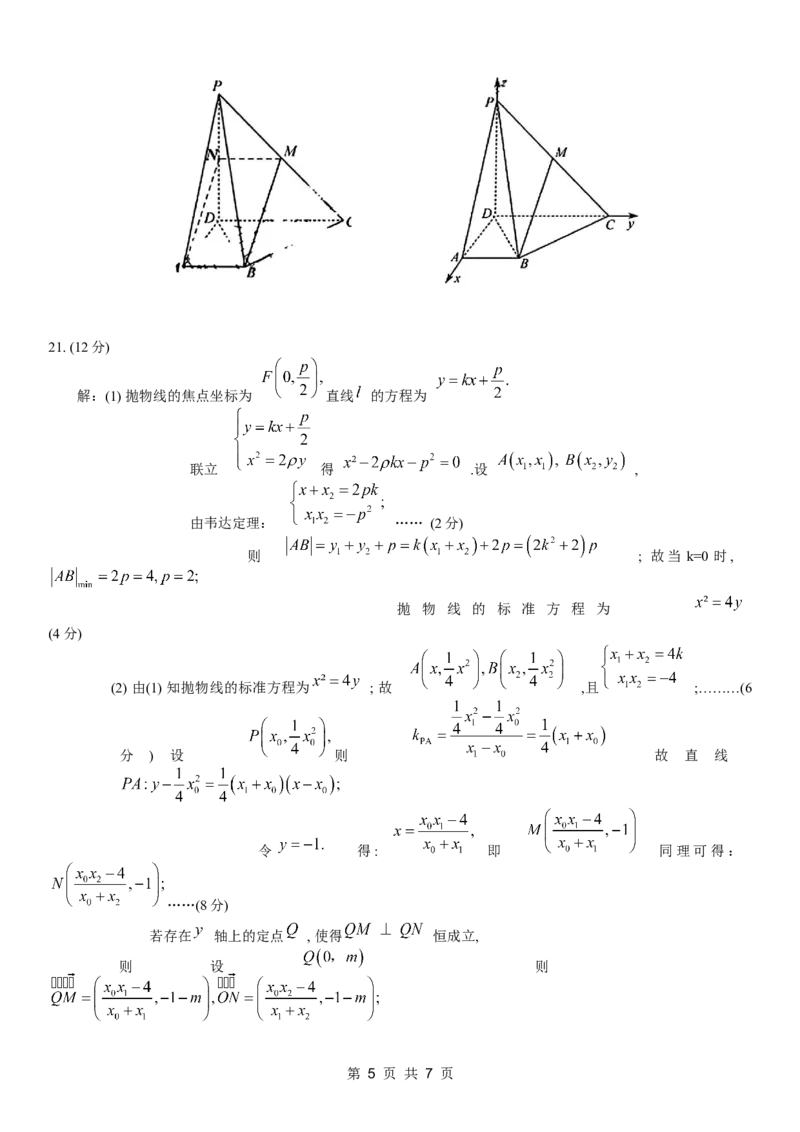
解: (1) 取 中点 ,则由 为 中点知 ;
故 四点共面;……………………(2分)
由 , ,
得 ,故 为平行四边形,故 ;
由 得 故 ; (4分)
得
由
故 …………………………………………(6分)
(2)以 为原点, 分别为 轴、 轴、 轴建立空间直角坐标系 ;
设 ,则
故 解得 ;…………………(7分)
故 ;
由 知 故 , 故 ; ,
设平面 的法向量 则
取 则 ………………………………(10分)
记直线 与平面 的夹角为 , 则
故直线 与平面 的夹角的正弦值为 ……………………………………(12分)
20.(12分)
解: (1) 由 得 ……………………………………………………………………(2分)
第 3 页 共 7 页因为 所以 且 故 是首项为2、公比为2的等比数列,所以
所以 ……………………………………………………………………………………(5分)
(2) 由 (1) 知 ,……………………………………………………(8分)
故
(12分)
第 4 页 共 7 页21. (12分)
解:(1) 抛物线的焦点坐标为 直线 的方程为
联立 得 .设 ,
由韦达定理: …… (2分)
则 ; 故当 k=0 时,
抛 物 线 的 标 准 方 程 为
(4分)
(2) 由(1) 知抛物线的标准方程为 ; 故 ,且 ;………(6
分 ) 设 则 故 直 线
令 得: 即 同理可得:
……(8分)
若存在 轴上的定点 , 使得 恒成立,
则 设 则
第 5 页 共 7 页故
解得 或
所以,定点 的坐标为 或 ………………………………………………………(12分)
22. (12分)
解 :( 1) 令 则 有 2 个 零 点 ;
定义域
当 时, 在 上恒成立, 在 上单调递增,至多有1个零点;
当 时,令 得
当 时, , 在区间 上单调递增;
当 时, , 在区间 上单调递减;
故 的极大值也是最大值为
因为 有2个零点,所以 解得
综上所述:实数 的取值范围是 (4分)
(2) 令 ,则 有2个零点 ;
即 两式相减得: ………(5分)
; 考 察 函 数
令 得 ;
当 时, , 在区间 上单调递增;
当 时 在区间 上单调递减;故 即 ;
由题意: 对任意 恒成立;
故: (7分)
第 6 页 共 7 页即:不等式 恒成立,两边取对数得:
令 则 恒成立,
所以 在 时恒成立…(9分)
令
则
若 即 则当 时
故 在 上单调递增,所以 恒成立,满足题意;
若 , 则当 时有 , 故 在 上单调递减,
所以当 时, ,不满足题意.
综上所述,正数 的取值范围为 ………………………………………(12分)
第 7 页 共 7 页