文档内容
深圳市高级中学 2025 届高三第二次诊断考试
数学
2024.11
(本试卷共4页,19小题,满分150分,考试用时120分钟)
一、单项选择题:本题共8小题,每小题5分,共40分.
1.已知集合 ,则 ( )
A. B. C. D.
2.直线 的倾斜角为 ,则 ( )
A. B. C. D.
3.已知圆锥的侧面展开图是圆心角为 且弧长为 的扇形,则该圆锥的体积为( )
A. B. C. D.
4.已知公差不为0的等差数列 中, 且 ,则 ( )
A.30 B. C. D.40
5.已知 ,则 ( )
A. B.3 C. D.4
6.在三棱锥 中, ,平面 平面 ,则三棱锥
外接球表面积为( )
A. B. C. D.
7.已知 都是正实数, ,则 的最小值为( )A.2 B. C. D.
8.已知函数 的定义域为 为奇函数, ,则( )
A. 为奇函数
B. 的图象关于直线 对称
C. 的最小正周期为4
D. 的图象关于点 对称
二、多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合
题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.已知正方体 棱长为1,下列结论正确的是( )
A.直线 与 所成角为
B.直线 到平面 的距离是
C.点 到直线 的距离为
D.平面 与平面 所成角的余弦值为
10.已知 为等差数列, 为等比数列, 的公差为 的公比为 , ,下列结论正确
的是( )
A.若 ,则 为递增数列
B.若 ,则 为递减数列
C.若 ,则 为递增数列
D.若 ,则 为递增数列
11.在锐角三角形 中, 外接圆的半径为 ,则( )A.
B.
C.
D.
三、填空题:本题共3小题,每小题5分,共15分.
12.若 , 为虚数单位,则 __________.
13. 是等比数列 的前 项和,已知 ,则 __________.
14.在三棱锥 中, 与 中点分别为 ,点 为 中点.若 在 上满足
在 上满足 ,平面 交 于点 ,且 ,则
__________.
四、解答题:本大题共 小题,共77分.解答应写出文字说明,证明过程或演算步骤.
15.(13分)记 的内角 所对的边分别是 的面积为 .若 ,
(1)求 ;
(2)若 ,求 的值.
16.(15分)我们知道关于 的二元一次方程表示直线,但有的二元二次方程也能表示直线,比如
表示的就是 和 两条直线.
(1)求方程 表示的直线与 轴围成的面积;
(2)若方程 表示的是两条直线,求 .
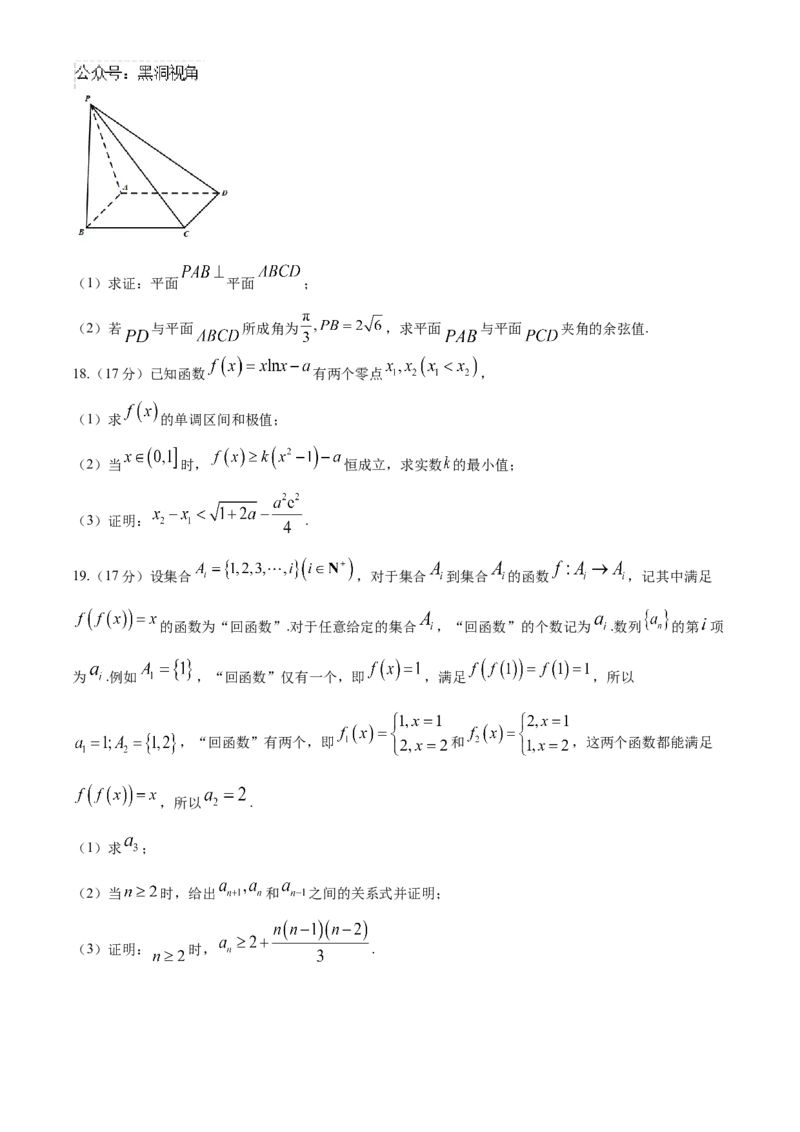
17.(15分)四棱锥 中,底面 为正方形, 为锐角.(1)求证:平面 平面 ;
(2)若 与平面 所成角为 ,求平面 与平面 夹角的余弦值.
18.(17分)已知函数 有两个零点 ,
(1)求 的单调区间和极值;
(2)当 时, 恒成立,求实数 的最小值;
(3)证明: .
19.(17分)设集合 ,对于集合 到集合 的函数 ,记其中满足
的函数为“回函数”.对于任意给定的集合 ,“回函数”的个数记为 .数列 的第 项
为 .例如 ,“回函数”仅有一个,即 ,满足 ,所以
,“回函数”有两个,即 和 ,这两个函数都能满足
,所以 .
(1)求 ;
(2)当 时,给出 和 之间的关系式并证明;
(3)证明: 时, .深圳市高级中学 2025 届高三第二次诊断考试数学参考答案
1 DACC AACD
9.BCD 10.AC 11.AC
12.1 13. 或 14.
14.解答:
在平面 上,使得 ,其中
,得
15.(1)
得 ,得
(2)
16.(1) 表示的直线为 和 ,
联立 ,得两直线交点为 ,两直线与 轴交点分别为 和
两直线与 轴围成的三角形面积为
(2)若方程 表示两条直线,则该方程必能表示为两个二元一次方程的乘积,
则,解得
17(1) 四边形 为正方形 ,又 ,且
平面 平面
平面 平面
(2)以 为原点 分别为 轴,过 作平面 的垂线,以该垂线为 轴
由(1)可知 轴在平面 内
由题意可得
易知平面 的法向量为
,得 ,
解得 或
为锐角,
,设平面 的法向量为,得 ,取 ,得
易得平面 的法向量为 ,设平面 与平面 夹角为 ,则
.
综上,平面 与平面 夹角的余弦值为 .
18.(1)
令 ,得
时, 单调递减, 时, 单调递增, 的极
小值为 ,无极大值
(2) ,即 ,令
时, 时, ,而 ,不合题意;
时,
,显然 为减函数
当 ,即 时,
则 单调递增且 ,
时, 单调递减
当 时,
时, 单调递增且使得 ,且 时, 单调递减, 时,
单调递增 ,不合题意.
综上 的最小值为 .
(3)当 时, ,若 ,则 ,则 在 没有零点,又 在
上单调递增,所以 最多只有1个零点,不合题意
,又
由(2)可知 ,解得
欲证 ,即证 ,即证
即证 ,即证
令
得 的最小值为 ,即 ,易知
,综上
19.(1)分别是
(2) 时, 分别表示集合 中“回函数”个数
中“回函数”的个数计算分两种情况:
i.若 ,则其他元素不可能对应到 ,否则通过两次对应后不可能到达自身,即其他 个
元素之间只能在内部对应,所以这种情况的“回函数”的个数为 ;
ii.若 ,由于一个元素经过两次对应必须回到自身,所以必有 ,
而除 和 之外的元素也不能对应 或 ,即其他 个元素只能在它们内部对应,所以“回函
数”的个数为 ,又 有 种选择,所以这种情况的“回函数”个数为 .
综上,
(3)易知
时, ,即 单调递增
时,,且 满足不等式
综上, 时, .