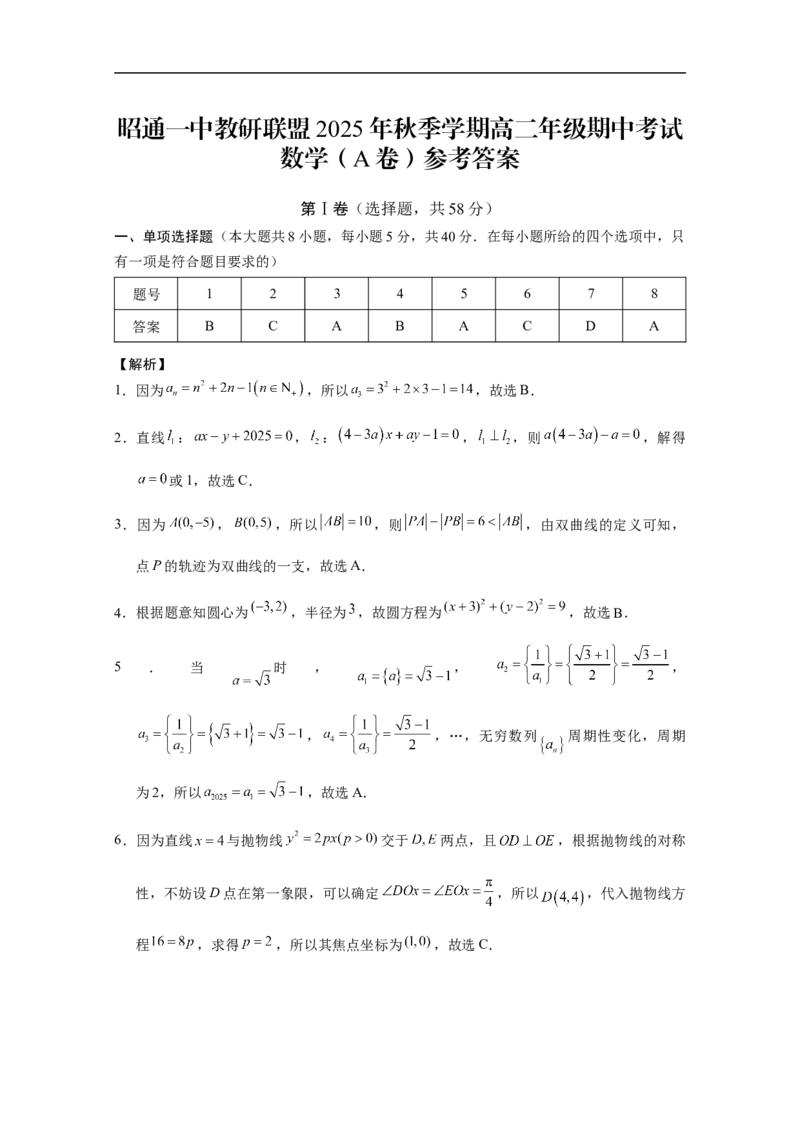文档内容
昭通一中教研联盟 2025 年秋季学期高二年级期中考试
数学(A 卷)参考答案
第Ⅰ卷(选择题,共58分)
一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题所给的四个选项中,只
有一项是符合题目要求的)
题号 1 2 3 4 5 6 7 8
答案 B C A B A C D A
【解析】
1.因为 ,所以 ,故选B.
2.直线 : , : , ,则 ,解得
或1,故选C.
3.因为 , ,所以 ,则 ,由双曲线的定义可知,
点P的轨迹为双曲线的一支,故选A.
4.根据题意知圆心为 ,半径为 ,故圆方程为 ,故选B.
5 . 当 时 , , ,
, ,…,无穷数列 周期性变化,周期
为2,所以 ,故选A.
6.因为直线 与抛物线 交于 两点,且 ,根据抛物线的对称
性,不妨设D点在第一象限,可以确定 ,所以 ,代入抛物线方
程 ,求得 ,所以其焦点坐标为 ,故选C.7.建立如图1空间直角坐标系 ,则 ,
, ,故点 到直线 的距离
,故选D.
图
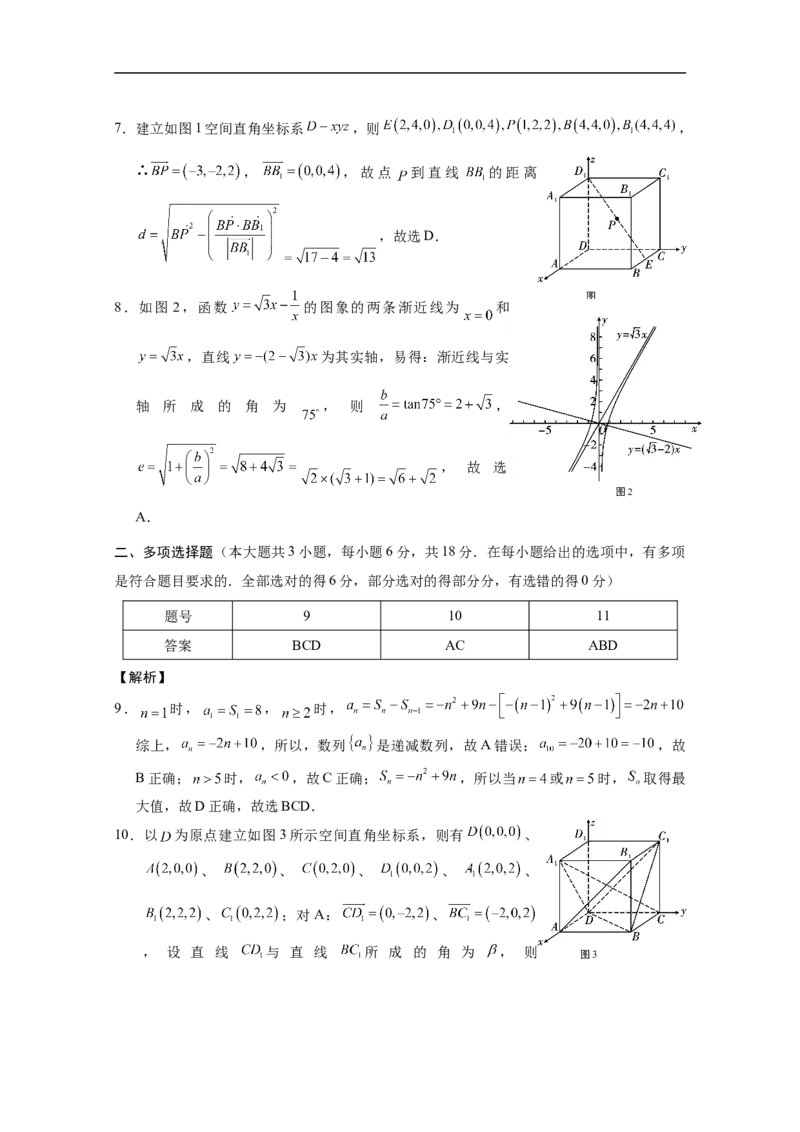
8.如图 2,函数 的图象的两条渐近线为 和
,直线 为其实轴,易得:渐近线与实
轴 所 成 的 角 为 , 则 ,
, 故 选
图2
A.
二、多项选择题(本大题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项
是符合题目要求的.全部选对的得6分,部分选对的得部分分,有选错的得0分)
题号 9 10 11
答案 BCD AC ABD
【解析】
9. 时, , 时,
综上, ,所以,数列 是递减数列,故A错误; ,故
B正确; 时, ,故C正确; ,所以当 或 时, 取得最
大值,故D正确,故选BCD.
10.以 为原点建立如图3所示空间直角坐标系,则有 、
、 、 、 、 、
、 ;对A: 、
, 设 直 线 与 直 线 所 成 的 角 为 , 则
图3,故直线 与直线 所成的角
为 ,故A正确;对B:由 轴 平面 ,则平面 的法向量可为 ,
又 ,则 ,设直线 与平面 所
成角为 ,则 ,则 ,故B错误;对C:
、 , 设 平 面 的 一 个 法 向 量 为 , 则 有
,取 ,则 ,设平面 与平面DCB的夹角为 ,
又平面 的一个法向量为 ,则 ,故
平面 与平面DCB的夹角为 ,故C正确;对D: 、
、 ,设平面 的法向量为 ,则有 ,
取 ,则 ,则点 到平面 的距离 ,故D错误,
故选AC.
11.对于A:由图可知,曲线 关于 轴对称,A选项正确;对于B:明显是 , 到原点
的距离最小,最小值为 ,所以B正确;对于C: , , 所在的圆的方程分
别为 , , ,曲线 与 轴围成的图形是
一个半圆,一个矩形和两个 圆,其面积为 ,故C错误;对
于D:由对称性知:Ω截直线 所得弦长可由 所在的圆截得的弦长加上一个矩形的长4,而 所在的圆的方程为 ,圆心 ,圆心到直线 的距
离 ,截得的弦长为 ,则所求弦长为 ,故 D 正确,故选
ABD.
第Ⅱ卷(非选择题,共92分)
三、填空题(本大题共3小题,每小题5分,共15分)
题号 12 13 14
答案
【解析】
12.在等差数列 中, , ,所以 ,
.
13.在平行六面体 中, , , ,
,如图4, ,则
.
.
14.[方法一]:点差法
图4
设 ,则 ,所以 ,所以 ,
取AB中点 ,分别过点A,B作准线 的垂线,垂足分别为 ,因为
, ,因为 为AB中点,所以 平行于x轴,因为 ,所以 ,则 ,即 .
[方法二]:【最优解】焦点弦的性质
记抛物线的焦点为F,因为 ,则以 为直径的圆与准线相切于点M,由抛
物线的焦点弦性质可知 ,所以 .
[方法三]:【通性通法】暴力硬算
由题知抛物线 的焦点为 ,设直线 的方程为 ,代
入 中 得 , 设 , 则
,同理有 ,由 ,即 .
又 ,所以
,得 .
四、解答题(共77分.解答应写出文字说明,证明过程或演算步骤)
15.(本小题满分13分)
解:(1)由题意对任意正整数 ,有 ,
令 时, ,即 ,可得 ; ……………………………………(2
分)
令 时, ,即 ,可得 .
………………………………………………(4分)
由 ,猜想: . …………………………………(6分)
(2)由(1)可知 ;
当 时,由 得 ,
则 , ………………………(8分)即 ,即 , ………………………………………(10分)
故 时, ,
………………………………(12分)
且 也适合上式,所以 .
…………………………………………………(13分)
16.(本小题满分15分)
(1)证明:不妨设 ,以 为原点,
所在直线分别为 轴,建立空间直角坐标系, 如 图
5,………………………………………(2分)
, , , ,
图5
, , ……………………………(4分)
因为 , ………………………………………(6分)
所以 . ………………………………………(7分)
(2)解: , , ………………………………(9分)
易知平面 的一个法向量为 , ………………………………(11分)
设直线 与平面 所成角为 ,则
, ……………………………(14分)
即直线 与平面 所成角的正弦值为 .
………………………………………………(15分)
(最后一句话不写也可不扣分1分,用几何法做酌情给分)
17.(本小题满分15分)
解:(1)因为双曲线E的渐近线方程为 ,所以 ,解得 , ………………………………………(1分)
从而 ,即 , ………………………………………(3分)
所以右焦点为 ,从而 ,解得 , ………………………………(5分)
抛物线C的标准方程和双曲线E的标准方程依次分别为 , .
………………………………………(7分)(一个方程一分)
(2)由题意直线 ,它过抛物线的焦点 ,如图6,
联立抛物线方程得 ,化简并整理得 ,
…………………………………(9分)
显然 , ,
图6
所以 , ………………………………………(11分)
点 到直线 的距离为 , …………………………………(13分)
所以 ,即 的面积为 .
………………………………(15分)
18.(本小题满分17分)
解:(1) , ,解得 ,
…………………………………(1分)
,
又 ,
, ………………………………………(3分)
即 ,解得 或 , ………………………………………(5分)当 时, ;
当 时, . ………………………………………(7分)
(2) 为等差数列,
,即 ,
,即 ,
解得 或 , ………………………………………(9分)
, ,
又 ,由等差数列性质知, ,
即 , ………………………………………(11分)
,即 ,解得 或 (舍去).
………………………………………(13分)
当 时, ,解得 ;
…………………………………………(15分)
当 时, ,解得 ,与 矛盾,无解.
综上, . ………………………………………(17分)
19.(本小题满分17分)
解:(1)由题可知 ,
直线 的方程为 ,可化为 ,
…………………………………………(1分)
直线 的方程为 ,可化为 ,
…………………………………(2分)则两式联立得 ,所以椭圆方程为 .
…………………………………(3分)
(2)①设直线 的方程为 , , ,
…………………………………(4分)
与椭圆 的方程: 联立消去 可得: ,
则 , ,………………………………………(6分)
所以
,
…………………………………………………(8分)
代入 ,可得 . ………………………(10分)
②易得,直线 的斜率存在.设直线 的方程为 ,
, ,如图7,联立直线 与圆 的方程,
消去 可得 ,
则 ,
图7
………………………………………(12分)
所以
, …………………………(14分)代入 ,可得 . ……………………(16分)
综上,直线 恒过定点 . ………………………………………(17分)