2005年湖北高考文科数学真题及答案_数学高考真题试卷_旧1990-2007·高考数学真题_1990-2007·高考数学真题·PDF_湖北

2005 年湖北高考文科数学真题及答案 本试卷分第I卷（选择题）和第II卷（非选择题）两部分. 满分150分. 考试时间120分钟. 第I部分（选择题 共60分） 注意事项： 1．答卷前，考生务必将自己的姓名、准考证号填写在试题卷和答题卡上，并将准考证号条 形码粘贴在答题卡上的指定位置. 2．每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑.如需改动，用橡皮 擦干净后，再选涂其他答案标号.答在试题卷上无效. 3．考试结束，监考人员将本试题卷和答题卡一并收回. 一、选择题：本大题共12小题，每小题5分，共60分. 在每小题给出的四个备选项中，只 有一项是符合题目要求的. 1．设P、Q为两个非空实数集合，定义集合P+Q={ab|aP,bQ},若P{0,2,5}, Q {1,2,6}，则P+Q中元素的个数是 （ ） A．9 B．8 C．7 D．6 2．对任意实数a，b，c，给出下列命题： ①“a b”是“ac bc”充要条件； ②“a5是无理数”是“a是无理数”的充 要条件③“a>b”是“a2>b2”的充分条件；④“a<5”是“a<3”的必要条件. 其中真命题的个数是 （ ） A．1 B．2 C．3 D．4 3．已知向量a=（－2，2），b=（5，k）.若|a+b|不超过5，则k的取值范围是 （ ） A．[－4，6] B．[－6，4] C．[－6，2] D．[－2，6] 4．函数y e|lnx|| x1|的图象大致是 （ ） 5．木星的体积约是地球体积的240 30 倍，则它的表面积约是地球表面积的 （ ） A．60倍 B．60 30倍 C．120倍 D．120 30倍 x2 y2 6．双曲线  1(mn  0)离心率为2，有一个焦点与抛物线 y2  4x的焦点重合， m n 则mn的值为 （ ） 3 3 16 8 A． B． C． D． 16 8 3 3 7．在 y  2x,y log x,y  x2,y cos2x这四个函数中，当 0 x  x 1时，使 2 1 2 第1页 | 共11页x  x f(x ) f(x ) f( 1 2) 1 2 恒成立的函数的个数是 （ ） 2 2 A．0 B．1 C．2 D．3 8．已知a、b、c是直线，是平面，给出下列命题： ①若a b,b c,则a//c； ②若a//b,b c,则a c； ③若a//,b ,则a//b； ④若a与b异面，且a//,则b与相交； ⑤若a与b异面，则至多有一条直线与a，b都垂直. 其中真命题的个数是 （ ） A．1 B．2 C．3 D．4 9．把一排6张座位编号为1，2，3，4，5，6的电影票全部分给4个人，每人至少分1张， 至多分2张，且这两张票具有连续的编号，那么不同的分法种数是 （ ） A．168 B．96 C．72 D．144  10．若sincos tan(0 ),则 （ ） 2        A．(0, ) B．( , ) C．( , ) D．( , ) 6 6 4 4 3 3 2  11．在函数y  x3 8x的图象上，其切线的倾斜角小于 的点中，坐标为整数的点的个数 4 是 （ ） A．3 B．2 C．1 D．0 12．某初级中学有学生270人，其中一年级108人，二、三年级各81人，现要利用抽样方 法抽取10人参加某项调查，考虑选用简单随机抽样、分层抽样和系统抽样三种方案， 使用简单随机抽样和分层抽样时，将学生按一、二、三年级依次统一编号为1，2，…， 270；使用系统抽样时，将学生统一随机编号1，2，…，270，并将整个编号依次分为10 段.如果抽得号码有下列四种情况： ①7，34，61，88，115，142，169，196，223，250； ②5，9，100，107，111，121，180，195，200，265； ③11，38，65，92，119，146，173，200，227，254； ④30，57，84，111，138，165，192，219，246，270； 关于上述样本的下列结论中，正确的是 （ ） A．②、③都不能为系统抽样 B．②、④都不能为分层抽样 C．①、④都可能为系统抽样 D．①、③都可能为分层抽样 第Ⅱ卷（非选择题 共90分） 注意事项： 第Ⅱ卷用0.5毫米黑色的签字或黑色墨水钢笔直接答在答题卡上.答在试题卷上无效. 二、填空题：本大题共4小题，每小题4分，共16分. 把答案填在答题卡相应位置上. 第2页 | 共11页x2 13．函数 f(x)  lg 4x 的定义域是 . x3 2 1 14．(x3  )4 (x )8的展开式中整理后的常数项等于 . x x 15．函数y |sinx|cosx1的最小正周期与最大值的和为 . 16．某实验室需购某种化工原料106千克，现在市场上该原料有两种包装，一种是每袋35 千克，价格为140元；另一种是每袋24千克，价格为120元. 在满足需要的条件下， 最少要花费 元. 三、解答题：本大题共6小题，共74分，解答时应写出文字说明、证明过程或演算步骤. 17．（本小题满分12分） 已知向量a (x2,x1),b (1x,t),若函数f(x)  ab在区间（－1，1）上是增函数， 求t的取值范围. 18．（本小题满分12分） 1 在△ABC中，已知tanB  3,cosC  ,AC 3 6 ，求△ABC的面积. 3 19．（本小题满分12分） 设数列{a }的前n项和为S=2n2，{b }为等比数列，且a b ,b (a a ) b . n n n 1 1 2 2 1 1 （Ⅰ）求数列{a }和{b }的通项公式； n n a （Ⅱ）设c  n ，求数列{c }的前n项和T. n b n n n 20．（本小题满分12分） 如图所示的多面体是由底面为ABCD的长方体被截面AECF所截面而得到的，其中AB=4， 1 BC=2，CC=3，BE=1. 1 （Ⅰ）求BF的长； （Ⅱ）求点C到平面AECF的距离. 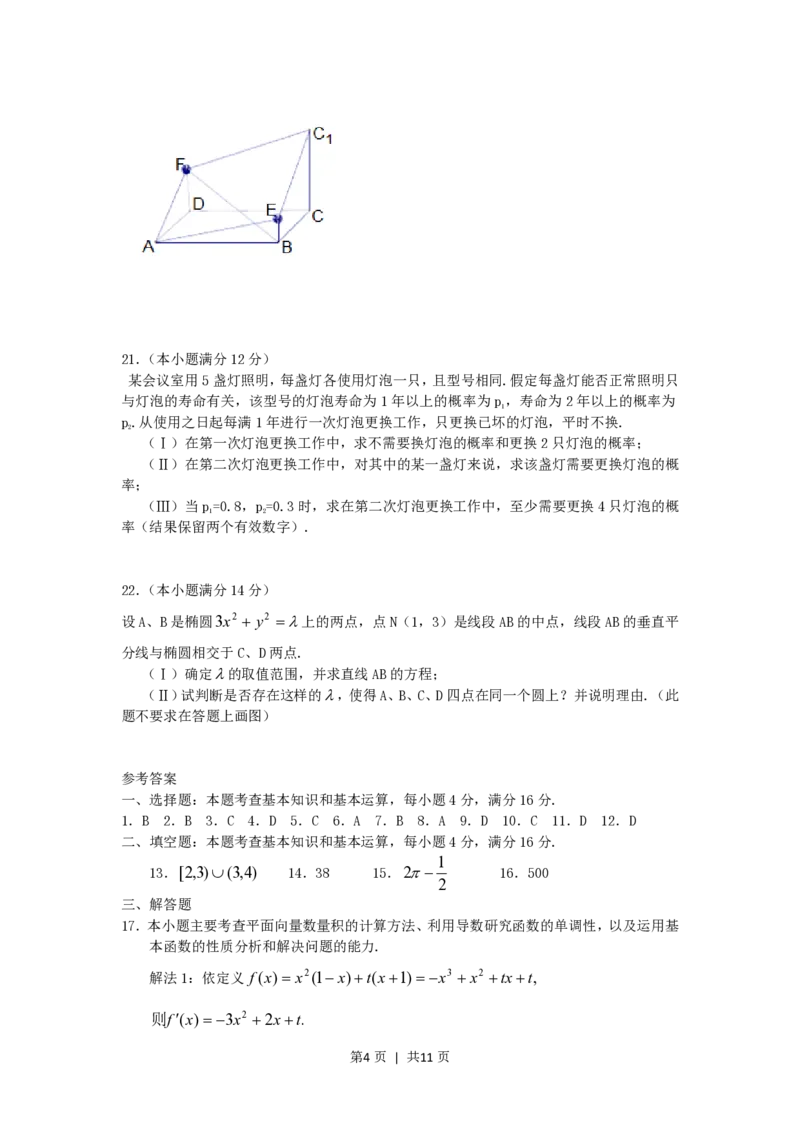1 第3页 | 共11页21．（本小题满分12分） 某会议室用5盏灯照明，每盏灯各使用灯泡一只，且型号相同.假定每盏灯能否正常照明只 与灯泡的寿命有关，该型号的灯泡寿命为1年以上的概率为p，寿命为2年以上的概率为 1 p.从使用之日起每满1年进行一次灯泡更换工作，只更换已坏的灯泡，平时不换. 2 （Ⅰ）在第一次灯泡更换工作中，求不需要换灯泡的概率和更换2只灯泡的概率； （Ⅱ）在第二次灯泡更换工作中，对其中的某一盏灯来说，求该盏灯需要更换灯泡的概 率； （Ⅲ）当p=0.8，p=0.3时，求在第二次灯泡更换工作中，至少需要更换4只灯泡的概 1 2 率（结果保留两个有效数字）. 22．（本小题满分14分） 设A、B是椭圆3x2  y2 上的两点，点N（1，3）是线段AB的中点，线段AB的垂直平 分线与椭圆相交于C、D两点. （Ⅰ）确定的取值范围，并求直线AB的方程； （Ⅱ）试判断是否存在这样的，使得A、B、C、D四点在同一个圆上？并说明理由.（此 题不要求在答题上画图） 参考答案 一、选择题：本题考查基本知识和基本运算，每小题4分，满分16分. 1．B 2．B 3．C 4．D 5．C 6．A 7．B 8．A 9．D 10．C 11．D 12．D 二、填空题：本题考查基本知识和基本运算，每小题4分，满分16分. 1 13．[2,3)(3,4) 14．38 15．2 16．500 2 三、解答题 17．本小题主要考查平面向量数量积的计算方法、利用导数研究函数的单调性，以及运用基 本函数的性质分析和解决问题的能力. 解法1：依定义 f(x)  x2(1x)t(x1)  x3  x2 txt, 则f (x)  3x2 2xt. 第4页 | 共11页若f(x)在(1,1)上是增函数,则在(1,1)上可设f (x)0.  f (x)0 t 3x2 2x,在区间(1,1)上恒成立,考虑函数g(x) 3x2 2x, 1 由于g(x)的图象是对称轴为x  ,开口向上的抛物线，故要使t 3x2 2x在区间 3 （－1，1）上恒成立 t  g(1),即t 5. 而当t 5时, f (x)在(1,1)上满足f (x) 0,即f(x)在(1,1)上是增函数. 故t的取值范围是t 5. 解法2：依定义 f(x)  x2(1x)t(x1)  x3  x2 txt, f (x)  3x2 2xt. 若f(x)在(1,1)上是增函数,则在(1,1)上可设f (x)0. f (x)的图象是开口向下的抛物线，  当且仅当f (1) t 10,且f (1) t 50时 f (x)在(1,1)上满足f (x) 0,即f(x)在(1,1)上是增函数. 故t的取值范围是t 5. 18．本小题主要考查正弦定理、余弦定理和三角形面积公式等基础知识，同时考查利用三角 公式进行恒等变形的技能和运算能力. 解法1：设AB、BC、CA的长分别为c、a、b， 3 1 由tanB  3,得B 60,sinB  ,cosB  . 2 2 2 2 又sinC  1cos2C  ,应用正弦定理得 3 bsinC 3 62 2 c   8. sinB 3 2 3 1 1 2 3 3 2 sin Asin(BC) sinBcosC cosBsinC       . 2 3 2 3 6 3 1 故所求面积S  bcsin A6 2 8 3. ABC 2 解法2：同解法一可得c=8，又由余弦定理得， 第5页 | 共11页a2 b2 c2 2bccosA.而cosA cos(BC) 1 1 3 2 2 6 1  cosBcosC sinBsinC        2 3 2 3 3 6  228 3 a 0, a  228 6  4 6  1 故所求面积S  acsinB 6 2 8 3 ABC 2 解法3：同解法1可得c=8. 又由余弦定理可得 1 b2  a2 c2 2accosB,即54 a2 642a8 ,a2 8a100. 2 所得a  4 6,a  4 6. B 60,0 C 90,30  A120. 1 2  a b b b 3 6 1 由  得,a  sinA sin30   3 2 3, sinA sinB sinB sinB 3 2 2 而a 4 6 3,舍去,故a 4 6. 2 1 故所求面积S  acsinB 6 2 8 3. ABC 2 19．本小题主要考查等差数列、等比数列基本知识和数列求和的基本方法以及运算能力. 解：（1）：当n 1时,a  S  2; 1 1 当n  2时,a  S S  2n2 2(n1)2  4n2, n n n1 故{a}的通项公式为a  4n2,即{a }是a  2,公差d  4的等差数列. n n n 1 1 设{b}的通项公式为q,则b qd b ,d  4,q  . n 1 1 4 1 2 故b b qn1 2 ,即{b }的通项公式为b  . n 1 4n1 n n 4n1 a 4n2 （II） c  n  (2n1)4n1,  n b 2 n 4n1 T c c  c [1341 542  (2n1)4n1], n 1 2  n  4T [14342 543  (2n3)4n1 (2n1)4n] n  两式相减得 1 3T 12(41 42 43  4n1)(2n1)4n  [(6n5)4n 5] n  3 1 T  [(6n5)4n 5]. 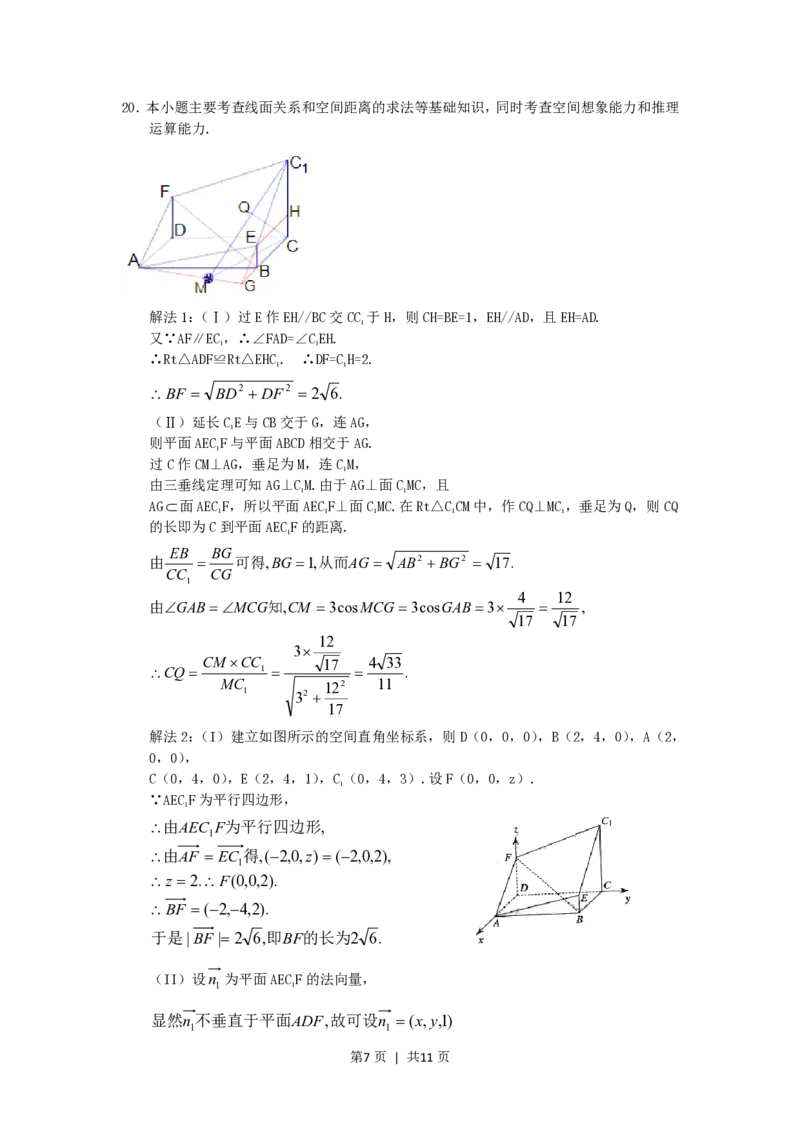n 9 第6页 | 共11页20．本小题主要考查线面关系和空间距离的求法等基础知识，同时考查空间想象能力和推理 运算能力. 解法1：（Ⅰ）过E作EH//BC交CC 于H，则CH=BE=1，EH//AD，且EH=AD. 1 又∵AF∥EC，∴∠FAD=∠CEH. 1 1 ∴Rt△ADF≌Rt△EHC. ∴DF=CH=2. 1 1 BF  BD2 DF2  2 6. （Ⅱ）延长CE与CB交于G，连AG， 1 则平面AECF与平面ABCD相交于AG. 1 过C作CM⊥AG，垂足为M，连CM， 1 由三垂线定理可知AG⊥CM.由于AG⊥面CMC，且 1 1 AG面AECF，所以平面AECF⊥面CMC.在Rt△CCM中，作CQ⊥MC，垂足为Q，则CQ 1 1 1 1 1 的长即为C到平面AECF的距离. 1 EB BG 由  可得,BG 1,从而AG  AB2 BG2  17. CC CG 1 4 12 由GAB MCG知,CM 3cosMCG 3cosGAB 3  , 17 17 12 3 CM CC 17 4 33 CQ  1   . MC 122 11 1 32  17 解法2：（I）建立如图所示的空间直角坐标系，则D（0，0，0），B（2，4，0），A（2， 0，0）， C（0，4，0），E（2，4，1），C（0，4，3）.设F（0，0，z）. 1 ∵AECF为平行四边形， 1 由AEC F为平行四边形, 1 由AF  EC 得,(2,0,z) (2,0,2), 1 z  2.F(0,0,2). BF (2,4,2). 于是| BF | 2 6,即BF的长为2 6. （II）设n 为平面AECF的法向量， 1 1 显然n不垂直于平面ADF,故可设n (x,y,1) 1 1 第7页 | 共11页 n AE 0, 0x4 y10 由 1 得   n AF 0, 2x0 y20  1 x 1, 4y10,  即   1 2x2 0,  y   .  4 又CC (0,0,3),设CC 与n 的夹角为a，则 1 1 1 CC n 3 4 33 cos 1 1   . |CC ||n | 1 33 1 1 3 1 1 16 ∴C到平面AECF的距离为 1 4 33 4 33 d |CC |cos3  . 1 33 11 21．本小题主要考查概率的基础知识和运算能力，以及运用概率的知识分析和解决实际问题 能力. 解：（I）在第一次更换灯泡工作中，不需要换灯泡的概率为 p5,需要更换2只灯泡的概 1 率为 C2p3(1 p )2; 5 1 1 （II）对该盏灯来说，在第1、2次都更换了灯泡的概率为（1-p）2；在第一次未更换 1 灯泡而在第二次需要更换灯泡的概率为p(1-p)，故所求的概率为 1 2 p (1 p )2  p (1 p ); 1 1 2 （III）至少换4只灯泡包括换5只和换4只两种情况，换5只的概率为p5（其中p为 （II）中所求，下同）换4只的概率为C1p4（1-p），故至少换4只灯泡的概率为 5 p  p5 C1p4(1 p). 3 5 又当p 0.8,p 0.3时,p 0.22 0.80.7 0.6 1 2 p 0.65 50.64 0.40.34. 3 即满2年至少需要换4只灯泡的概率为0.34. 22．本小题主要考查直线、圆和椭圆等平面解析几何的基础知识以及推理运算能力和综 合解决问题的能力. （I）解法1：依题意，可设直线AB的方程为y  k(x1)3,代入3x2  y2 ，整 理得 (k2 3)x2 2k(k 3)x(k 3)2 0. ① 设A(x ,y ),B(x ,y ),则x ,x 是方程①的两个不同的根， 1 1 2 2 1 2 第8页 | 共11页  4[(k2 3)3(k 3)2]0 ② 2k(k 3) 且x  x  .由N(1,3)是线段AB的中点，得 1 2 k2 3 x  x 1 2 1,k(k 3)  k2 3. 2 解得k=-1，代入②得，>12，即的取值范围是（12，+）. 于是，直线AB的方程为y3 (x1),即x y4 0. 解法2：设A(x ,y ),B(x ,y ),则有 1 1 2 2 3x2  y2 ,  1 1 3(x x )(x  x )(y  y )(y  y ) 0. 3x2  y2  1 2 1 2 1 2 1 2  2 2 3(x  x ) 依题意，x  x ,k   1 2 . 1 2 AB y  y 1 2 N(1,3)是AB的中点,x  x  2,y  y 6,从而k  1.  1 2 1 2 AB 又由N(1,3)在椭圆内,312 32 12. 的取值范围是(12,). 直线AB的方程为y3 (x1),即x y40. （ II ） 解 法 1 ： CD垂直平分AB,直线CD的方程为y3 x1,即x y20.代入椭圆方程，  整理得 4x2 4x40. ③ 又设C(x ,y ),D(x ,y ),CD的中点为M(x ,y ),则x ,x 是方程③的两根， 3 3 4 4 0 0 3 4 1 1 3 x  x  1,且x  (x  x )   ,y  x 2 , 3 4 0 2 3 4 2 0 0 2 1 3 即M( , ). 2 2 于是由弦长公式可得 1 |CD| 1( )2| x x | 2(3). ④ k 3 4 将直线AB的方程x y4 0,代入椭圆方程得 4x2 8x160. ⑤ 第9页 | 共11页同理可得 | AB| 1k2| x x | 2(12). ⑥ 1 2 当12时, 2(3)  2(12).,| AB||CD|.  假设在在>12，使得A、B、C、D四点共圆，则CD必为圆的直径，点M为圆心.点M到 直线AB的距离为 1 3 |  4| | x  y 4| 2 2 3 2 d  0 0   . ⑦ 2 2 2 于是，由④、⑥、⑦式和勾股定理可得 AB 9 12 3 CD |MA|2|MB|2 d2| |2   | |2 . 2 2 2 2 2 |CD| 故当12时，A、B、C、D四点均在以M为圆心， 为半径的圆上. 2 （注：上述解法中最后一步可按如下解法获得： A、B、C、D共圆△ACD为直角三角形，A为直角| AN |2|CN || DN |,即 | AB| |CD| |CD| ( )2 ( d)( d). ⑧ 2 2 2 12 由⑥式知，⑧式左边= . 2 2(3) 3 2 2(3) 3 2 由④和⑦知，⑧式右边=(  )(  ) 2 2 2 2 3 9 12    , 2 2 2 ∴⑧式成立，即A、B、C、D四点共圆 解法2：由（II）解法1及12. CD垂直平分AB,直线CD方程为y3 x1,代入椭圆方程，整理得  4x2 4x40. ③ 将直线AB的方程x y40,代入椭圆方程，整理得 4x2 8x160. ⑤ 2 12 1 3 解③和⑤式可得 x ,  ,x  . 1 2 2 3,4 2 1 1 1 3 3 3 1 3 3 3 不妨设 A(1 12,3 12),C( , ),D( , ) 2 2 2 2 2 2 第10页 | 共11页3 12  3 3 3 12 ∴CA( , ) 2 2 3 12  3 3 3 12 DA( , ) 2 2 计算可得CADA0，∴A在以CD为直径的圆上. 又B为A关于CD的对称点，∴A、B、C、D四点共圆. （注：也可用勾股定理证明AC⊥AD） 第11页 | 共11页