贵州省名校协作体2023-2024学年高三上学期联考（一）数学参考答案(1)_2023年11月_01每日更新_22号_2024届贵州省名校协作体高三上学期联考（一）

贵州省名校协作体 2023-2024 学年高三联考（一） 数学参考答案 一、单项选择题: 本题共 8小题，每小题 5分，共 40 分. 题号 1 2 3 4 5 6 7 8 答案 B D B C A B B C 8.C 【解析】设事件A为“该球员投球得分”，事件B为“该球员投中3分球得分”， 2 3 1 4 23 由全概率公式：P(A)  P(B)P(A| B) P(B)P(A| B)      ，故选：C 3 4 3 5 30 二、多项选择题: 本题共 4小题，每小题 5分，全部选对得5分，不分选对得2 分，有错选的得 0分，共 20分。 题号 9 10 11 12 答案 AD ACD ABC CD 12.CD 【解析】当x0时，f(x)3x2 33(x1)(x1)，所以当x(,1)时，f(x)单调递增；当x(1,0] 时， f(x)单调递减；又当x(0,)时， f(x)单调递增，所以 f(x)的图像大致如下： 对于A选项，方程 f(x)1有三个不相等的根，A错误； 对于B选项，方程 f(x)m的根等价于函数 f(x)的图像与 y m的交点的横坐 标，根据图像知实数m的取值范围是  0,1    3 ，故B错误； 对于 C 选项，令 f(x)t ，方程 f(t)1的根为t  3,t 0,t e1，而 1 2 3 f(x) 3有一个根， f(x)0有一个根， f(x)e1有三个根，且这五个根互不相等，所以C正确； 对于 D 选项，令 f(x)t ，则方程 t2 2ata2 10 的根为 t a1， t a1 ，因为方程 1 2 [f(x)]2 2af(x)a2 10有四个不相等的实数根，结合 f(x)的图像知  a13  a13 1a13 0a11  或 或 或 ， 1a13 0a11  a10 0a11 解得a[0,1](2,4)，故D正确，故选CD. 数学答案 第 1 页 共 6 页 {#{QQABIQCAogAgAAIAABhCQwXQCgMQkAEACKoOxAAEIAAAAANABCA=}#}三、填空题：本题共 4 小题，每小题 5 分，共 20 分。 题号 13 14 15 16 1 答案 2 5 2 2 4 16．【解析】当n为奇数时，a a 3n1；当n时为偶数时，a a 3n1. n2 n n2 n 设数列{a }的前n项和S ， n n 则S a a a a ...a ， 16 1 2 3 4 16 a a a ...a (a a )...(a a )， 1 3 5 15 2 4 14 16 a (a 2)(a 10)(a 24)(a 44)(a 70)(a 102)(a 140)(5172941) 1 1 1 1 1 1 1 1 8a 392928a 484486， 1 1 1 1 则a  . 故答案为 . 1 4 4 四、解答题：本题共 6 小题，其中 17 题 10 分，18-22 题每题 12 分，共 70 分。 17．【解析】（1）根据统计图表中的数据，结合平均数的计算方法，可得本次统考中数学考试成绩样本的平 均数为 x600.02800.221000.531200.21400.03100................2分 2  s2 16000.024000.2200.534000.216000.03 248 ............................5分 （2）由（1）可知X ~N(100,15.752)....................................................................................................6分 0.95440.6826 所以P(84.25 X 131.5)   0.8185.....................................................................9分 2 因为0.8185  0.8,所以本次考试试题的有效性符合要求........................................................................10分 18．【解析】（1）由S  S a a a a a a 0a a 0.................................2分 3 9 4 5 6 7 8 9 6 7 则a a 11....................................................................................................................................3分 12 1 设{a }的公差为d ，则a 11d 111111d 11d 2 n 1 则a a (n1)d 112(n1)2n13 n 1 所以数列{a }的通项公式为a 2n13.............................................................................................5分 n n （2）由题可知T  a  a  a  a  a 100 1 2 6 7 100   T a a a  a a .................................................................................................7分 100 1 2 6 7 100   T  S  S S 2S S 100 6 100 6 6 100     26111 10011187   ...................................................................................................10分 2 2 8872 数学答案 第 2 页 共 6 页 {#{QQABIQCAogAgAAIAABhCQwXQCgMQkAEACKoOxAAEIAAAAANABCA=}#}T 8872..........................................................................................................................................12分 100 3 19．【解析】（1）因为△ABC的面积为 ， 2 1 3 所以 bcsinA ，即bcsinA 3，...............................................................................................1分 2 2   因为ABAC 1，所以bccosA1，...............................................................................................3分 bcsinA 所以  3，得tan A 3 ， bccosA    因为A0, ，所以A ..................................................................................................................5分  2 3 π 2π （2）结合（1）可得A ,BCπA ， 3 3 a b c 由a 3，则根据正弦定理有   2，得b2sinB,c2sinC，............................7分 sinA sinB sinC 根据余弦定理有a2 b2c22bccosA，得b2c2 3bc， 2π  所以b2 c2 3bc 34sinBsinC 34sinBsin  B .......................................................9分  3   π 32 3sinBcosB2sin2B4 3sin2Bcos2B42sin 2B ，  6  π 2π  π π π 又V ABC 为锐角三角形，则有B 0, , B 0, ，得B  , ，  2 3  2 6 2 π π 5π  π 1  所以2B   , ，所以sin2B    ,1  ，..................................................................11分 6 6 6   6 2   π 故b2 c2 42sin2B   5,6  ................................................................................................12分  6 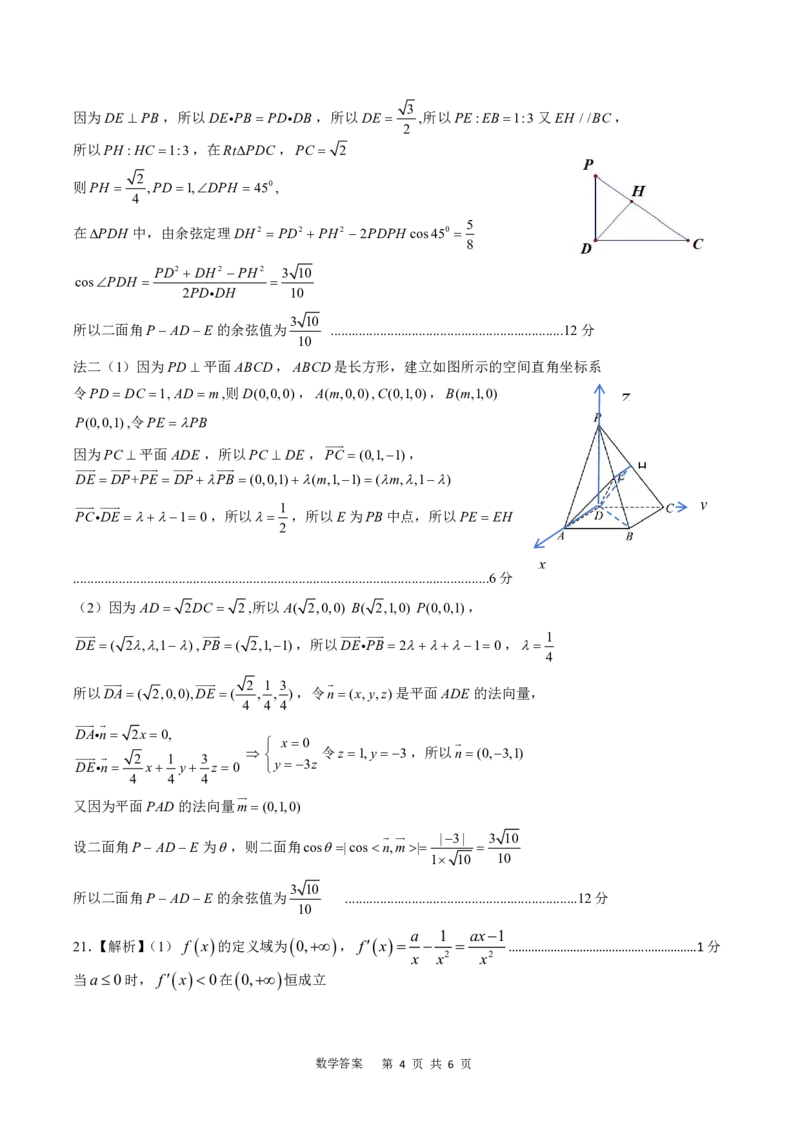20．【解析】法一： （1）过E作EH //BC交PC与H ，连接DH 因为ABCD是长方形，AD//BC ，所以AD//EH ，所以ADHE四点共面 PC 平面ADE ，所以PC  DH , 又因为PD DC ，所以H 为PC的中点 又EH //BC，所以E为PB中点，所以PE  BE .............................................................6分 （2）令PD DC 1，则AD 2 ,因为PD平面ABCD，所以PD AD， 因为AD DC，PDDC  D ，所以AD平面PDC ， 所以AD DH ，所以PDH 为二面角P ADE的平面角 在RtPDB中DB AD2 DC2  3，PB BD2 PD2 2 数学答案 第 3 页 共 6 页 {#{QQABIQCAogAgAAIAABhCQwXQCgMQkAEACKoOxAAEIAAAAANABCA=}#}3 因为DE  PB，所以DEPB PDDB ，所以DE  ,所以PE:EB1:3又EH //BC， 2 所以PH :HC 1:3，在RtPDC ，PC  2 2 则PH  ,PD1,DPH 450, 4 5 在PDH 中，由余弦定理DH2  PD2 PH2 2PDPHcos450  8 PD2 DH2 PH2 3 10 cosPDH   2PDDH 10 3 10 所以二面角P ADE的余弦值为 ..................................................................12分 10 法二（1）因为PD平面ABCD，ABCD是长方形，建立如图所示的空间直角坐标系 令PD  DC 1,AD m,则D(0,0,0)，A(m,0,0),C(0,1,0)，B(m,1,0) z P(0,0,1),令PE PB  因为PC 平面ADE ，所以PC  DE，PC (0,1,1)，      H DE  DP+PE  DPPB(0,0,1)(m,1,1)(m,,1)   1 y PCDE 10，所以 ，所以E为PB中点，所以PE  EH 2 x ......................................................................................................................6分 （2）因为AD  2DC  2,所以A( 2,0,0) B( 2,1,0) P(0,0,1)，     1 DE ( 2,,1),PB( 2,1,1)，所以DEPB 210， 4   2 1 3  所以DA( 2,0,0),DE ( , , )，令n(x,y,z)是平面ADE 的法向量， 4 4 4   DAn 2x0,  x0    2 1 3   令z 1,y 3，所以n(0,3,1) DEn x y z 0 y 3z 4 4 4  又因为平面PAD的法向量m(0,1,0)   |3| 3 10 设二面角P ADE为，则二面角cos|cosn,m|  1 10 10 3 10 所以二面角P ADE的余弦值为 ..................................................................12分 10 a 1 ax1 21．【解析】（1） f  x 的定义域为 0,， f x    ………………………………………………….1分 x x2 x2 当a0时， f x 0在 0,恒成立 数学答案 第 4 页 共 6 页 {#{QQABIQCAogAgAAIAABhCQwXQCgMQkAEACKoOxAAEIAAAAANABCA=}#}1 1 当a 0时，令 f x 0，得x  ；令 f x 0，得0 x a a 综上所述：当a0时， f  x 的单调递减区间为 0,  1 1  当a 0时， f  x 的单调递减区间为0, ，单调递增区间为 , ……………...….5分  a a  （2）不妨设x  x ，则不等式等价于 f  x  f  x  2  x x  1 2 1 2 1 2 即 f  x 2x  f  x 2x 1 1 2 2 令g  x  f  x 2x，则函数g  x 在 0,1 上单调递减…………………………………………………….8分 a 1 则g x  f x 2  20在 0,1 上恒成立………………………………………….……….9分 x x2 1  1 所以a 2x在 0,1 上恒成立，所以a 2x  x  x min 1  2  2  1 因为 y2x 在0, 上单调递减，在 ,1递增，所以2x 2 2……….……….11分     x  2   2  x 所以实数a的取值范围为(,2 2]…………………...……………………………………………………...12分 22．【解析】（1）由题点A、F、P三点共线，点B、F、P三点共线 1 1     则PAF 的周长为 PA  AF  PF  AF  AF  PF  PF 4a， 2 2 2 1 2 1 2 则PFF 的周长为 FF  PF  PF 2c2a， 1 2 1 2 1 2 4a 8 由题  ， 3a 4c 2a2c 7 c 3 椭圆C的离心率为e  ...................................................................................................5分 a 4 x 2 y 2 （2）设P  x ,y  ,A  x ,y  ,B  x ,y  且 y 0，则有 0  0 1，即b2x2 a2y2 a2b2 0 0 1 1 2 2 0 a2 b2 0 0     由题F c,0 ,F c,0 由FP AF,F P BF 1 2 1 1 2 2  y      0  x c,y cx ,y   0 0 1 1  y 可得 ，则 1     y   x c,y cx ,y  0 0 0 2 2   y 2  x c x 0 yc  y x c  0 由题设直线AP:x 0 yc，联立 y 0 x2 y2   1 a2 b2   化简整理可得 b2 x c 2 a2y 2 y2 2b2cy  x c  yb4y 2 0 0 0 0 0 0 b4y 2 b4y  0成立，故 y y  0 ， y  0 0 1 b2 x c 2 a2y 2 1 b2 x c 2 a2y 2 0 0 0 0 b4y 同理可得 y  0 2 b2 x c 2 a2y 2 0 0 数学答案 第 5 页 共 6 页 {#{QQABIQCAogAgAAIAABhCQwXQCgMQkAEACKoOxAAEIAAAAANABCA=}#}   1 1  2b2x 2 2a2y 2 2b2c2 2 a2 c2 50 y 0   y  y     0 b4 0 = b2  7 （定值）.................................12分 1 2 x 2 y 2 另解（2）：设P  x ,y  ,A  x ,y  ,B  x ,y  且 y 0，则由 0  0 1，即有b2x2 a2y2 a2b2① 0 0 1 1 2 2 0 a2 b2 0 0      x c,y cx ,y      0 0 1 1 由题F c,0 ,F c,0 ，由FP AF,F P BF ，可得 1 2 1 1 2 2       x c,y cx ,y 0 0 2 2  cx y x  0 c,y  0  1  1  则 cx y x  0 c,y  0  2  1  点A在椭圆上，则b2x2 a2y2 a2b2，则将上式代入整理得b2 cx c 2 a2y2 a2b22② 1 1 0 0 a2 c2 2cx a2 c2 2cx ②①整理化简得 0 ，同理可得 0 b2 b2   2 a2 c2 50 =  （定值）...................................................................................................12分 b2 7 数学答案 第 6 页 共 6 页 {#{QQABIQCAogAgAAIAABhCQwXQCgMQkAEACKoOxAAEIAAAAANABCA=}#}