2005年福建高考文科数学真题及答案_数学高考真题试卷_旧1990-2007·高考数学真题_1990-2007·高考数学真题·PDF_福建

2005 年福建高考文科数学真题及答案 本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共150分，考试用时120分钟. 考试结束后，将本试卷和答题卡一并交回. 第I卷（选择题 共60分） 注意事项： 1．答第I卷前，考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上． 2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑．如需改动，用橡皮擦 干净后，再选涂其它答案标号．不能答在试题卷上． 一、选择题：本大题共12小题，每小题5分，共60分. 在每小题给出的四个选项中，只有 一项是符合题目要求的. P | x|| x1|1,x Q {x| xN},则P Q 1．已知集合 R|，  等于 （ ） A．P B．Q C．{1，2} D．{0，1，2} 2x1 0 2．不等式 3x1 的解集是 （ ） 1 1 1 1 {x| x   或x  } {x|  x  } 3 2 3 2 A． B． 1 1 {x| x  } {x| x   } 2 3 C． D． {a } a a 16,a 1,则a 3．已知等差数列 n 中， 7 9 4 12的值是 （ ） A．15 B．30 C．31 D．64 y cos2x 4．函数 在下列哪个区间上是减函数 （ ）    3   [ , ] [ , ] [0, ] [ ,] 4 4 4 4 2 2 A． B． C． D． 5．下列结论正确的是 （ ） 1 1 x0且x1时,lgx 2 当x0时, x  2 A．当 lgx B． x 1 1 当x  2时,x 0 x  2时,x x x C． 的最小值为2 D．当 无最大值 f(x)  axb 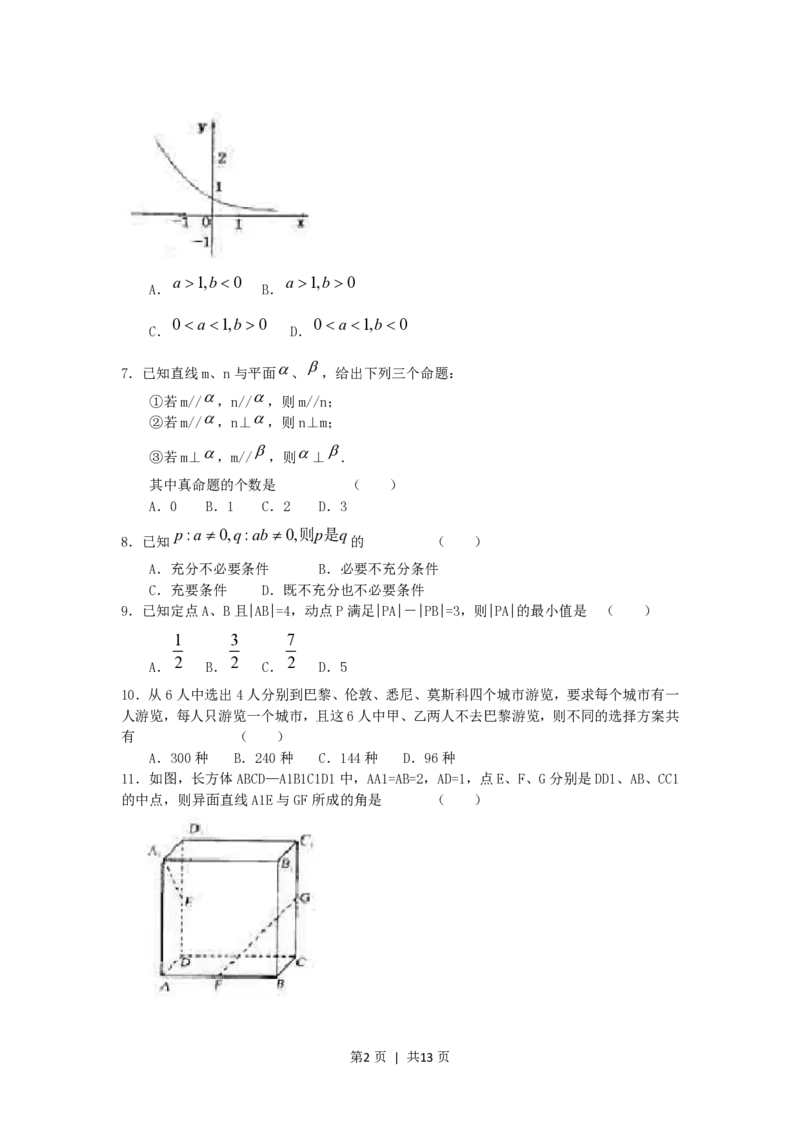6．函数 的图象如图，其中a、b为常数，则下列结论正确的是 （ ） 第1页 | 共13页a 1,b0 a 1,b 0 A． B． 0 a 1,b 0 0 a 1,b 0 C． D．   7．已知直线m、n与平面 、 ，给出下列三个命题：   ①若m// ，n// ，则m//n；   ②若m// ，n⊥ ，则n⊥m；     ③若m⊥ ，m// ，则 ⊥ . 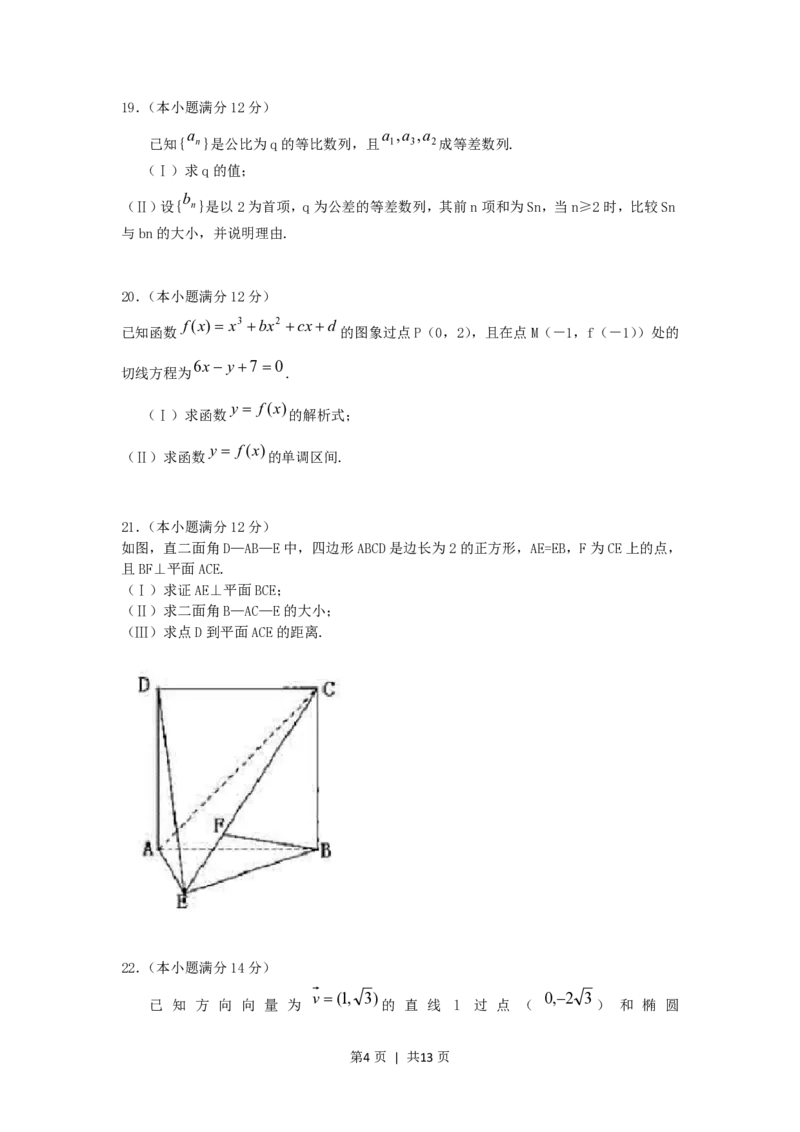其中真命题的个数是 （ ） A．0 B．1 C．2 D．3 p:a  0,q:ab  0,则p是q 8．已知 的 （ ） A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 9．已知定点A、B且|AB|=4，动点P满足|PA|－|PB|=3，则|PA|的最小值是 （ ） 1 3 7 2 2 2 A． B． C． D．5 10．从6人中选出4人分别到巴黎、伦敦、悉尼、莫斯科四个城市游览，要求每个城市有一 人游览，每人只游览一个城市，且这6人中甲、乙两人不去巴黎游览，则不同的选择方案共 有 （ ） A．300种 B．240种 C．144种 D．96种 11．如图，长方体ABCD—A1B1C1D1中，AA1=AB=2，AD=1，点E、F、G分别是DD1、AB、CC1 的中点，则异面直线A1E与GF所成的角是 （ ） 第2页 | 共13页15  arccos 5 4 A． B． 10  arccos 5 2 C． D． f(x) f(2) 0 f(x) 12． 是定义在R上的以3为周期的偶函数，且 ，则方程 =0在区间 （0，6）内解的个数的最小值是 （ ） A．5 B．4 C．3 D．2 第Ⅱ卷（非选择题 共90分） 二、填空题：本大题共4小题，每小题4分，共16分. 把答案填在答题卡的相应位置. 1 2 x  )6 x 13．（ 展开式中的常数项是 （用数字作答）. AB (k,1),AC (2,3),则k 14．在△ABC中，∠A=90°， 的值是 . 2x y40  ,则x3y x y30 15．非负实数x、y满足 的最大值为 . 16．把下面不完整的命题补充完整，并使之成为真命题. f(x) 3log x g(x) g(x) 若函数 2 的图象与 的图象关于 对称，则函数 = . （注：填上你认为可以成为真命题的一种情形即可，不必考虑所有可能的情形） 三、解答题：本大题共6小题，共74分. 解答应写出文字说明，证明过程或演算步骤. 17．（本小题满分12分）  1   x 0,sinxcosx  2 5 已知 . sinxcosx （Ⅰ）求 的值； sin2x2sin2 x （Ⅱ）求 1tanx 的值. 18．（本小题满分12分） 1 2 与 2 5 甲、乙两人在罚球线投球命中的概率分别为 . （Ⅰ）甲、乙两人在罚球线各投球一次，求恰好命中一次的概率； （Ⅱ）甲、乙两人在罚球线各投球二次，求这四次投球中至少一次命中的概率. 第3页 | 共13页19．（本小题满分12分） a a ,a ,a 已知{ n}是公比为q的等比数列，且 1 3 2成等差数列. （Ⅰ）求q的值； b （Ⅱ）设{ n}是以2为首项，q为公差的等差数列，其前n项和为Sn，当n≥2时，比较Sn 与bn的大小，并说明理由. 20．（本小题满分12分） f(x)  x3 bx2 cxd 已知函数 的图象过点P（0，2），且在点M（－1，f（－1））处的 6x y7 0 切线方程为 . y  f(x) （Ⅰ）求函数 的解析式； y  f(x) （Ⅱ）求函数 的单调区间. 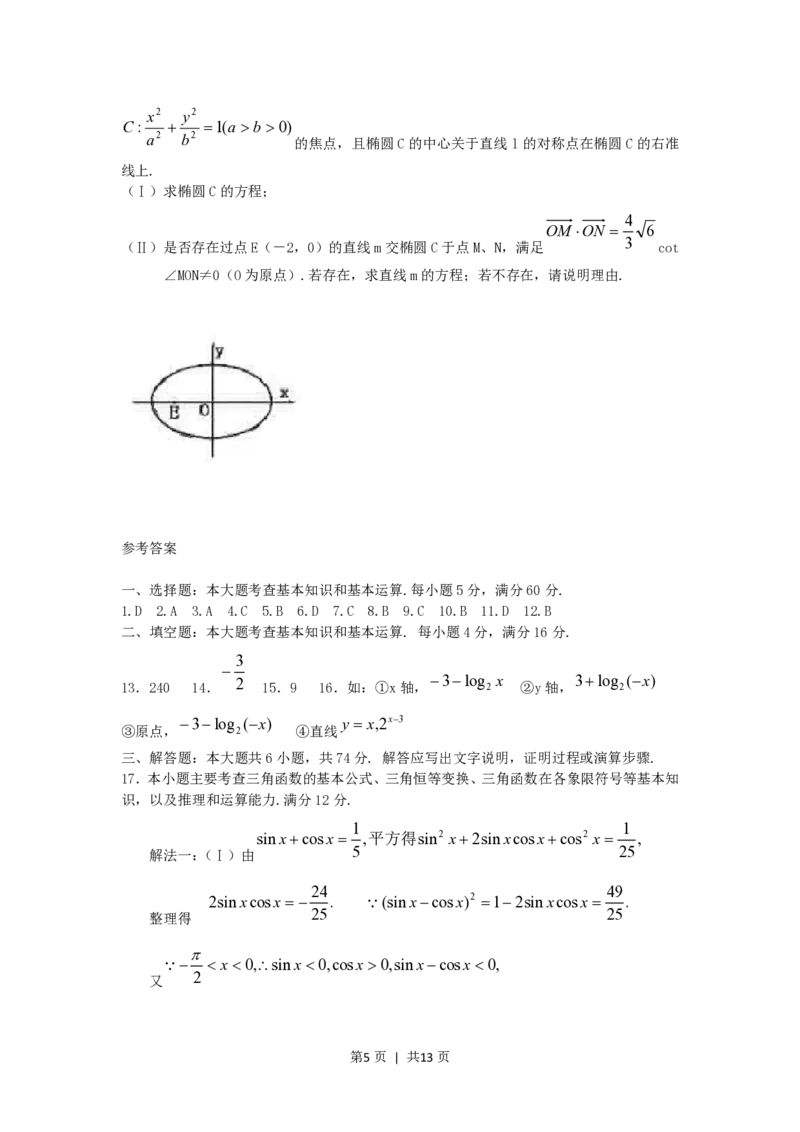21．（本小题满分12分） 如图，直二面角D—AB—E中，四边形ABCD是边长为2的正方形，AE=EB，F为CE上的点， 且BF⊥平面ACE. （Ⅰ）求证AE⊥平面BCE； （Ⅱ）求二面角B—AC—E的大小； （Ⅲ）求点D到平面ACE的距离. 22．（本小题满分14分） v (1, 3) 0,2 3 已 知 方 向 向 量 为 的 直 线 l 过 点 （ ） 和 椭 圆 第4页 | 共13页x2 y2 C:  1(a b 0) a2 b2 的焦点，且椭圆C的中心关于直线l的对称点在椭圆C的右准 线上. （Ⅰ）求椭圆C的方程； 4 OM ON  6 3 （Ⅱ）是否存在过点E（－2，0）的直线m交椭圆C于点M、N，满足 cot ∠MON≠0（O为原点）.若存在，求直线m的方程；若不存在，请说明理由. 参考答案 一、选择题：本大题考查基本知识和基本运算.每小题5分，满分60分. 1.D 2.A 3.A 4.C 5.B 6.D 7.C 8.B 9.C 10.B 11.D 12.B 二、填空题：本大题考查基本知识和基本运算. 每小题4分，满分16分. 3  2 3log x 3log (x) 13．240 14． 15．9 16．如：①x轴， 2 ②y轴， 2 3log (x) y  x,2x3 ③原点， 2 ④直线 三、解答题：本大题共6小题，共74分. 解答应写出文字说明，证明过程或演算步骤. 17．本小题主要考查三角函数的基本公式、三角恒等变换、三角函数在各象限符号等基本知 识，以及推理和运算能力.满分12分. 1 1 sinxcosx  ,平方得sin2 x2sinxcosxcos2 x  , 5 25 解法一：（Ⅰ）由 24 49 2sinxcosx   . (sinxcosx)2 12sinxcosx  .  25 25 整理得    x 0,sinx 0,cosx 0,sinxcosx 0,  2 又 第5页 | 共13页7 sinxcosx   . 5 故 24 1   sin2x2sin2 x 2sinx(cosxsinx) 2sinxcosx(cosxsinx) 25 5 24     . 1tanx sinx cosxsinx 7 175 1 （Ⅱ） cosx 5  1 sinxcosx  , ①  5 ②  sin2cos2 x 1. 解法二：（Ⅰ）联立方程 1 sinx  cosx, 5 25cos2 x5cosx120, 由①得 将其代入②，整理得  3 sinx   ,  3 4   5 cosx   或cosx  .    x 0, 5 5 2 4  cosx  .   5 7 sinxcosx   . 5 故 3 4 3 2( ) 2( )2 sin2x2sin2 x 2sinxcosx2sin2 x 5 5 5 24     . 1tanx sinx 3 175 1  cosx 5 1 4 5 （Ⅱ） 18．本小题主要考查概率的基本知识，运用数学知识解决问题的能力，以及推理和运算能力. 满分12分. 解：（Ⅰ）依题意，记“甲投一次命中”为事件A，“乙投一次命中”为事件B，则 1 2 1 3 P(A)  ,P(B)  ,P(A)  ,P(B)  . 2 5 2 5 ∵“甲、乙两人各投球一次，恰好命中一次”的事件为AB AB 1 3 1 2 1 P(AB AB)  P(AB)P(AB)      . 2 5 2 5 2 1 . 2 答：甲、乙两人在罚球线各投球一次，恰好命中一次的概率为 （Ⅱ）∵事件“甲、乙两人在罚球线各投球二次均不命中”的概率为 1 1 3 3 9 P      2 2 5 5 100 第6页 | 共13页∴甲、乙两人在罚球线各投球两次至少有一次命中的概率 9 91 P 1P 1  . 100 100 91 . 100 答：甲、乙两人在罚球线各投球二次，至少有一次命中的概率为 19．本小题主要考查等差数列，等比数列及不等式的基本知识，考查利用分类讨论思想分析 问题和解决问题的能力. 满分12分. 2a  a a ,即2a q2  a a q, a  0,2q2 q10. （Ⅰ）由题设 3 1 2 1 1 1  1 1 q 1或 . 2 n(n1) n2 3n q 1,则S  2n 1 . n 2 2 （Ⅱ）若 (n1)(n2) n 2时,S b  S  0. n n n1 2 S b . 当 故 n n 1 n(n1) 1 n2 9n q   ,则S  2n ( )  . 2 n 2 2 4 若 (n1)(n10) n 2时,S b  S   , n n n1 4 当 nN ,当2 n9时,S b ;当n 10时,S b ;当n11时,S b . 故对于  n n n n n n 20．本小题主要考查函数的单调性、导数的应用等知识，考查运用数学知识分析问题和解决 问题的能力. 满分12分. f(x) f(x)  x3 bx2 cx2, 解：（Ⅰ）由 的图象经过P（0，2），知d=2，所以 f (x) 3x2 2bxc. M(1, f(1)) 6x y7 0 由在 处的切线方程是 ，知 6 f(1)7 0,即f(1) 1, f (1) 6. 32bc 6, 2bc  3,  即  解得b c  3. 1bc21. bc 0, f(x)  x3 3x2 3x2. 故所求的解析式是 f (x) 3x2 6x3. 令3x2 6x30,即x2 2x10. （Ⅱ） x 1 2,x 1 2. x 1 2,或x 1 2时, f (x) 0; 解得 1 2 当 第7页 | 共13页1 2  x 1 2时, f (x)0. 当 f(x) x3 3x2 3x2在(,1 2) (1 2,1 2) 故 内是增函数，在 内是减函数， (1 2,) 在 内是增函数. 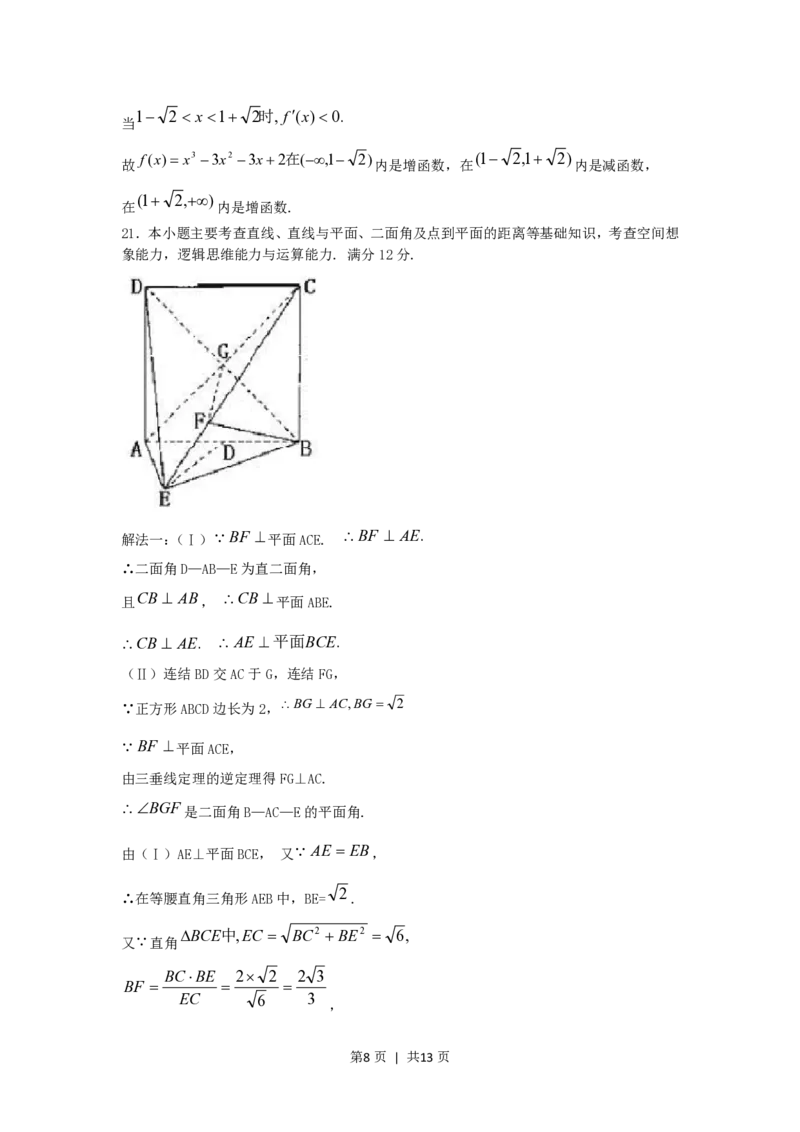21．本小题主要考查直线、直线与平面、二面角及点到平面的距离等基础知识，考查空间想 象能力，逻辑思维能力与运算能力. 满分12分. 解法一：（Ⅰ） BF 平面ACE. BF  AE. ∴二面角D—AB—E为直二面角， CB  AB CB  且 ， 平面ABE. CB  AE. AE 平面BCE. （Ⅱ）连结BD交AC于G，连结FG， BG AC,BG 2 ∵正方形ABCD边长为2，  BF 平面ACE， 由三垂线定理的逆定理得FG⊥AC. BGF 是二面角B—AC—E的平面角. 由（Ⅰ）AE⊥平面BCE， 又 AE  EB， 2 ∴在等腰直角三角形AEB中，BE= . BCE中,EC  BC2 BE2  6, 又直角 BCBE 2 2 2 3 BF    EC 6 3 ， 第8页 | 共13页2 3 BF 3 6 直角BFG中,sinBGF    . BG 2 3 6 arcsin . 3 ∴二面角B—AC—E等于 EO  AB （Ⅲ）过点E作 交AB于点O. OE=1. ∵二面角D—AB—E为直二面角，∴EO⊥平面ABCD. 1 1  S h  S EO. 设D到平面ACE的距离为h， V DACE V EACD , 3 ACE 3 ACD 1 1 ADDCEO 221 2 2 2 3 h    . 1 1 3 AEEC 2 6  AE 平面BCE， AE  EC. 2 2 2 3 . 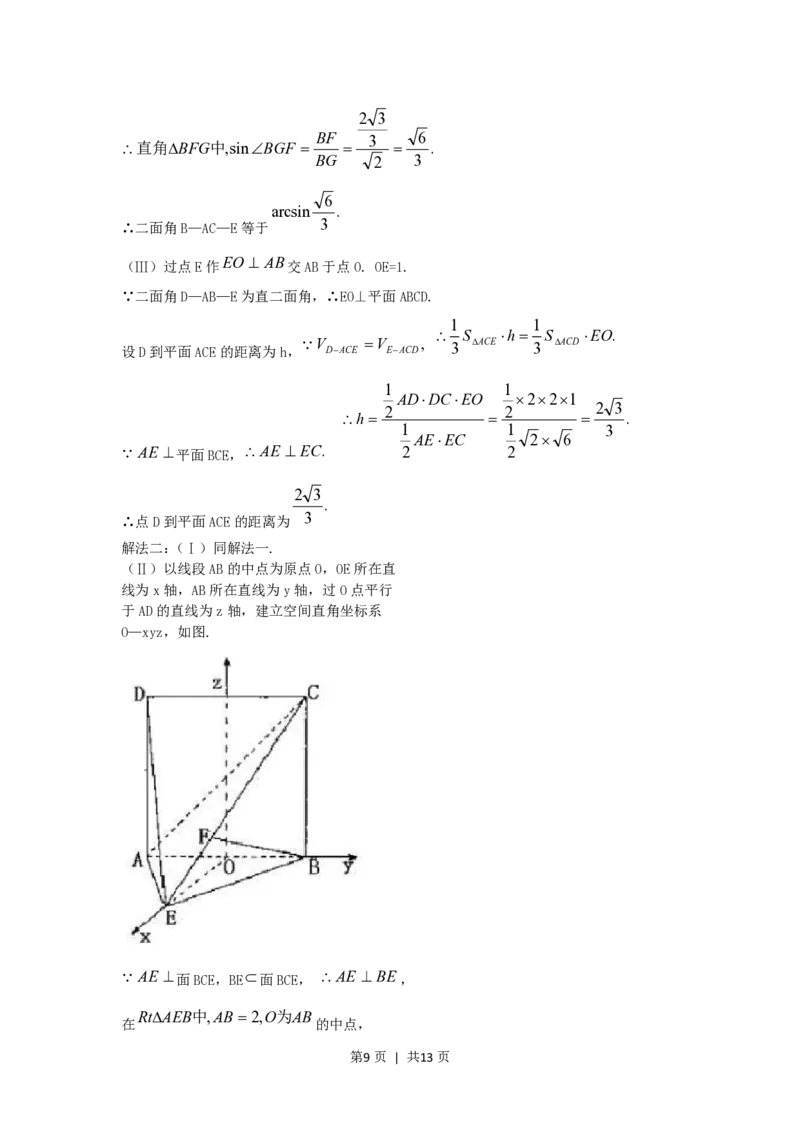3 ∴点D到平面ACE的距离为 解法二：（Ⅰ）同解法一. （Ⅱ）以线段AB的中点为原点O，OE所在直 线为x轴，AB所在直线为y轴，过O点平行 于AD的直线为z轴，建立空间直角坐标系 O—xyz，如图.  AE 面BCE，BE面BCE， AE  BE， RtAEB中,AB  2,O为AB 在 的中点， 第9页 | 共13页OE 1. A(0,1,0),E(1,0,0),C(0,1,2). AE (1,1,0),AC (0,2,2). n (x,y,z) 设平面AEC的一个法向量为 ，  AEn 0, x y 0, 即    ACn 0, 2y2z 0. 则 y  x,  z  x, 解得 x 1, n (1,1,1) 令 得 是平面AEC的一个法向量. m (1,0,0) 又平面BAC的一个法向量为 ， m,n 1 3 cos(m,n)    . |m||n| 3 3 3 arccos . 3 ∴二面角B—AC—E的大小为 AD (0,0,2) （III）∵AD//z轴，AD=2，∴ ， | ADn| 2 2 d | AD||cos AD,n    3. |n| 3 3 ∴点D到平面ACE的距离 22．本小题主要考查直线、椭圆及平面向量的基本知识，平面解析几何的基本方法和综合解 题能力.满分14分. l: y  3x3 3 （I）解法一：直线 ， ① 3 y   x l 3 过原点垂直 的直线方程为 ， ② 3 x  . 2 解①②得 l ∵椭圆中心O（0，0）关于直线 的对称点在椭圆C的右准线上， a2 3   2 3. c 2 l ∵直线 过椭圆焦点，∴该焦点坐标为（2，0）. 第10页 | 共13页x2 y2  1. c  2,a2 6,b2  2. 6 2 故椭圆C的方程为 ③ l: y  3x3 3 解法二：直线 . q p  3 2 3  2 2  q  3 1. 设原点关于直线 l 对称点为（p，q），则  p 解得p=3. l ∵椭圆中心O（0，0）关于直线 的对称点在椭圆C的右准线上， a2  3. c l ∵直线 过椭圆焦点，∴该焦点坐标为（2，0）. x2 y2  1. c  2,a2 6,b2  2. 6 2 故椭圆C的方程为 ③ x ,y x ,y （II）解法一：设M（ 1 1），N（ 2 2）. x m: y  k(x2) 当直线m不垂直 轴时，直线 代入③，整理得 (3k2 1)x2 12k2x12k2 6 0, 12k2 12k2 6 x  x   ,x x  , 1 2 3k2 1 1 2 3k2 1 12k2 12k2 6 2 6(1k2) |MN | 1k2 (x x )2 4x x  1k2 ( )2 4  , 1 2 1 2 3k2 1 3k2 1 3k2 1 |2k | d  1k2 点O到直线MN的距离 4 4 cosMON  OM ON  6cotMON, |OM ||ON |cosMON  6 0, 3 即 3 sinMON 4 2 4 |OM ||ON|sinMON  6,S  6.|MN|d  6, 3 OMN 3 3 4 4 6 |k | k2 1  6(3k2 1). 3 即 1 3 k2  ,k   . 3 3 整理得 第11页 | 共13页2 S  6 当直线m垂直x轴时，也满足 OMN 3 . 3 2 3 y  x , 3 3 故直线m的方程为 3 2 3 y   x , 3 3 x  2. 或 或 OM ON  0 经检验上述直线均满足 . 3 2 3 y  x , 3 3 所以所求直线方程为 3 2 3 y   x , 3 3 x  2. 或 或 x ,y x ,y 解法二：设M（ 1 1），N（ 2 2）. x m: y  k(x2) 当直线m不垂直 轴时，直线 代入③，整理得 12k2 x  x   , (3k2 1)x2 12k2x12k2 6 0, 1 2 3k2 1 ∵E（－2，0）是椭圆C的左焦点， ∴|MN|=|ME|+|NE| a2 a2 c 2 12k2 2 6(k2 1) e( x )e( x ) (x x )2a ( )2 6  . = c 1 c 2 a 1 2 6 3k2 1 3k2 1 以下与解法一相同. x ,y x ,y 解法三：设M（ 1 1），N（ 2 2）. m:x ty2 (t2 3)y2 4ty20. 设直线 ，代入③，整理得 4t 2 y  y  ,y y  , 1 2 t2 3 1 2 t2 3 4t 8 24t2 24 | y  y | (y  y )4y y  ( )2   . 1 2 1 2 1 2 t2 3 t2 3 (t2 3)2 4 4 cosMON  OM ON  6cotMON, |OM ||ON |cosMON  6 0, 3 即 3 sinMON 4 2 |OM ||ON|sinMON  6,S  6. 3 OMN 3 第12页 | 共13页24t2 24 1 . S  S S  |OE|| y  y | OMN OEM OEN 2 1 2 (t2 3)2 24t2 24 2 6 ∴ (t2 3)2 =3 ，整理得 t4 3t2. t   3, t 0. 解得 或 3 2 3 3 2 3 y  x , y   x , 3 3 3 3 x  2. 故直线m的方程为 或 或 OM ON  0. 经检验上述直线均满足 3 2 3 3 2 3 y  x , y   x , 3 3 3 3 x  2. 所以所求直线方程为 或 或 第13页 | 共13页