贵阳市2023年普通高中高三年级质量监测试卷数学答案(1)_2023年11月_0211月合集_2024届贵州省贵阳市普通高中高三上学期11月质量监测

贵阳市 2023 年普通高中高三年级质量监测试卷 数学参考答案与评分建议 题号 1 2 3 4 5 6 7 8 9 10 11 12 选项 A D B B C C B A AB BC ABC ACD 13. 160 1 14.a = − 2  5 7 15.x = (或x =− ,x = 等) 6 6 6 28 2 16. 3 1 17. 解：（1）∵A+B= C,A+B+C =， 2 2  ∴C = ,A+B= 3 3 2 由余弦定理得c2 =a2 +b2 −2abcos ，即c2 =a2 +b2 +ab ① 3 3c 5c ∵a+c=2b②，由①②得a = ,b= ， 7 7 a 3 2 3 3 3 3 由正弦定理得sinA= sinC = sin =  = . c 7 3 7 2 14 …………………………………………………5分 15 3 （2）∵ABC的面积为 ， 4 1 15 3 ∴ absinC = ， 2 4 1 3 5 3 15 3 即  c c = ， 2 7 7 2 4 ∴c=7， 数学参考答案与评分建议 第 1 页（共6页） {#{QQABRQKAggCIAAJAARhCAwVQCACQkBGACAoGAEAIIAAAgANABCA=}#}5 3 3 15 3 所以AB边上的高h =bsinA= 7 = . 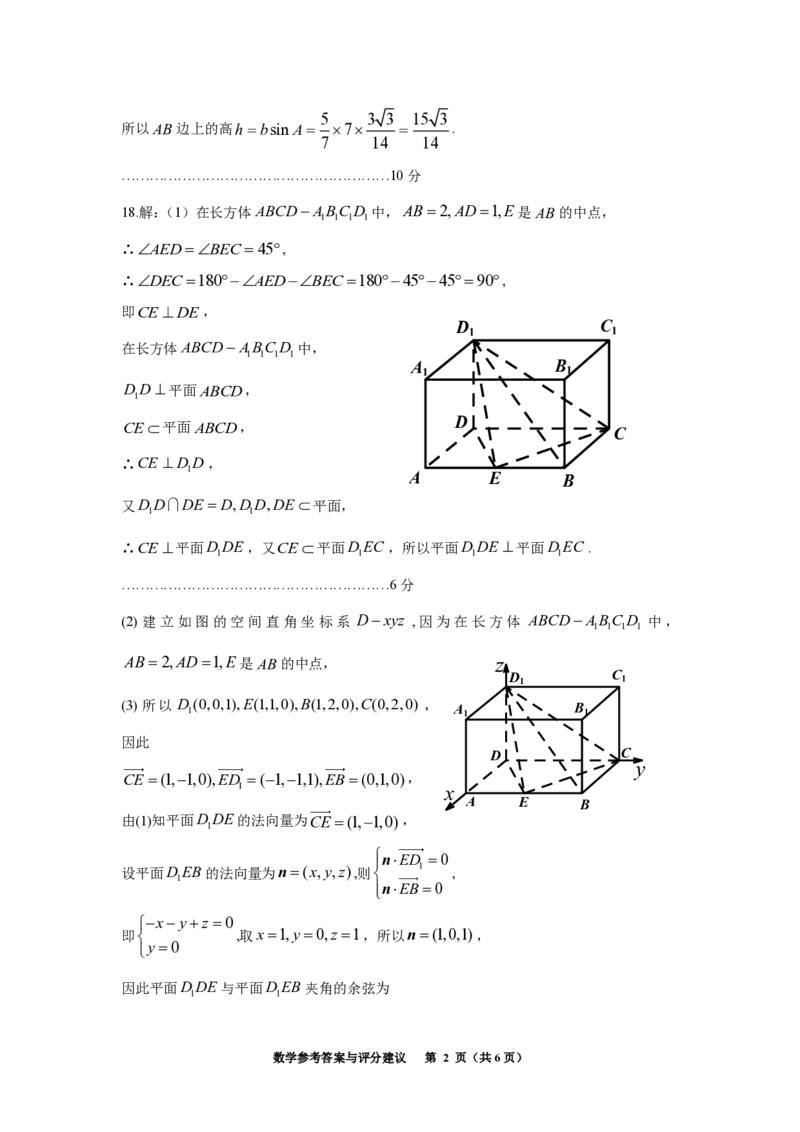7 14 14 …………………………………………………10分 18.解：（1）在长方体ABCD−ABC D 中，AB=2,AD=1,E是AB的中点， 1 1 1 1 ∴AED=BEC =45, ∴DEC=180−AED−BEC=180−45−45=90, 即CE⊥DE， D C 1 1 在长方体ABCD−ABC D 中， 1 1 1 1 A B 1 1 DD ⊥平面ABCD， 1 D CE平面ABCD， C ∴CE ⊥ DD， 1 A E B 又DD DE = D,DD,DE 平面， 1 1 ∴CE ⊥平面DDE，又CE平面DEC ，所以平面DDE ⊥平面DEC . 1 1 1 1 …………………………………………………6分 (2) 建立如图的空间直角坐标系 D−xyz ,因为在长方体 ABCD−ABC D 中， 1 1 1 1 AB=2,AD=1,E是AB的中点， z D 1 C 1 (3) 所以 D 1 (0,0,1),E(1,1,0),B(1,2,0),C(0,2,0) ， A 1 B 1 因此 D C y CE =(1,−1,0),ED =(−1,−1,1),EB=(0,1,0)， 1 x A E B 由(1)知平面DDE的法向量为CE =(1,−1,0)， 1  nED =0 设平面DEB的法向量为n=(x,y,z),则 1 , 1 nEB=0 −x− y+z =0 即 ,取x=1,y=0,z =1，所以n=(1,0,1)， y =0 因此平面DDE与平面DEB夹角的余弦为 1 1 数学参考答案与评分建议 第 2 页（共6页） {#{QQABRQKAggCIAAJAARhCAwVQCACQkBGACAoGAEAIIAAAgANABCA=}#}CEn 11+(−1)0+01 1 cos= = = . CE n 2 2 2 …………………………………………………12分 a (1−2n) 19. 解:（1）由题意得a =a 2n−1，S = 1 =a 2n −a ， n 1 n 1−2 1 1 a 2n −a +1 所以b = 1 1 =， n a 2n−1 1 即a 2n −a +1=a 2n−1对于所有nN*恒成立, 1 1 1 2a =a 因此 1 1 ，解得a =1,=2， −a +1=0 1  1 所以{a }的通项公式为a =12n−1 =2n−1. n n …………………………………………………6分 c n−1 （2）由（1）知c =log 2n−1 =n−1， n = ， n 2 a 2n−1 n 0 1 2 n−2 n−1 T = + + +...+ + ① n 20 21 22 2n−2 2n−1 1 0 1 2 n−2 n−1 T = + + +...+ + ② 2 n 21 22 23 2n−1 2n 1 1 [1−( )n−1] 1 1 1 1 n−1 2 2 n−1 n+1 ①−②得 T = + +...+ − = − =1− 2 n 21 22 2n−1 2n 1 2n 2n 1− 2 n+1 所以T =2− . n 2n−1 …………………………………………………12分 2 1 20.解：(1)设A = “从第i个盒子中取到红球”，则P(A)= ,P(A )= i 1 3 1 3 2 2 1 1 5 P(A )=P(AA )+P(AA )=P(A)P(A | A)+P(A)P(A | A) =  +  = ； 2 1 2 1 2 1 2 1 1 2 1 3 3 3 3 9 …………………………………………………4分 （2）∵P(A )=P(A A )+P(A A )=P(A )P(A | A )+P(A )P(A | A ) n n−1 n n−1 n n−1 n n−1 n−1 n n−1 2 1 1 1 = P(A ) +[1−P(A )] = P(A )+ n−1 3 n−1 3 3 n−1 3 数学参考答案与评分建议 第 3 页（共6页） {#{QQABRQKAggCIAAJAARhCAwVQCACQkBGACAoGAEAIIAAAgANABCA=}#}1 1 1 ∴P(A )− = [P(A )− ] n 2 3 n−1 2 1 1 2 1 1 1 所数列{P(A )− }是首项为P(A)− = − = ，公比为 的等比数列， n 2 1 2 3 2 6 3 1 1 1 1 1 1 因此P(A )− = ( )n−1，∴P(A )= + ( )n；（经验证n=1也成立） n 2 6 3 n 2 2 3 …………………………………………………8分 （3）X 的可能值为1,2， 1 1 1 1 1 1 P(X =1)= P(A )=1−P(A )= − ( )n−1,P(X =2)= P(A )= + ( )n−1, n−1 n−1 2 2 3 n−1 2 2 3 所以X 的分布列为 X 1 2 P 1 − 1 ( 1 )n−1 1 + 1 ( 1 )n−1 2 2 3 2 2 3 1 1 1 1 1 1 3 1 1 E(X)=1[ − ( )n−1]+2[ + ( )n−1]= + ( )n−1. 2 2 3 2 2 3 2 2 3 3 3 1 1 3 1 1 由于  + ( )n−1≤ + ( )1−1 =2， 2 2 2 3 2 2 3 3 所以  E(X)≤2. 2 …………………………………………………12分 21.解：（1）由题意得 A(−2,0),B(2,0) ,设 M(m,n),N(m,−n),(m0,m2) ，则 m2 +n2 =4， n n 直线PA的方程为y = (x+2)，直线PB的方程为y =− (x−2)， m+2 m−2 −n2 −n2 y2 = (x+2)(x−2)= (x2 −4)= x2 −4, m2 −4 −n2 所以轨迹E的方程为x2 − y2 =4(x2). …………………………………………………6分 （2）当定向直线l的倾斜角为90时，设l:x=t,(|t|≥2)， x=t 由 得C(t, t2 −4),D(t,− t2 −4)， x2 − y2 =4 数学参考答案与评分建议 第 4 页（共6页） {#{QQABRQKAggCIAAJAARhCAwVQCACQkBGACAoGAEAIIAAAgANABCA=}#}当AC ⊥ AD时，ACAD=0,(t+2)(t+2)− t2 −4 t2 −4 =0 ∴t =−2， 此时l:x=−2经过点A（A,C,D三点重合），不满足题意. 当定向直线l的倾斜角不为90时，假设存在定向直线l:y =kx+t ， y =kx+t 由 得(1−k2)x2 −2ktx−t2 −4=0， x2 − y2 =4 当1−k2 0,=4(t2 −4k2 +4)0时, 2kt −t2 −4 设C(x ,y ),D(x ,y )，则x +x = ,x x = 1 1 2 2 1 2 1−k2 1 2 1−k2 由AC ⊥ AD得,ACAD =0,即(x +2)(x +2)+(kx +t)(kx +t)=0， 1 2 1 2 因此(1+k2)xx +(2+kt)(x +x )+t2 +4=0， 1 2 1 2 −t2 −4 2kt (1+k2) +(2+kt) +t2 +4=0， 1−k2 1−k2 化简得k(t−2k)=0， ∴k =0或t =2k， 当k =0时,经验证,满足条件；当t =2k时,l: y =kx+2k =k(x+2) 过点A，不满足条件， 综上所述，当k =0即直线l 的一个方向向量为(1,0)时,AC ⊥ AD. …………………………………………………12分 22.解（1）由 f(x)=−xeax+1得 f(x)=−eax+1(ax+1),x(−,+), (i)当a=0时， f(x)=−e0，函数 f(x)在(−,+)上单调递减， 1 1 1 (ⅱ)当a0时，x=− , f(x)=0；x− , f(x)0；x− , f(x)0； a a a 1 1 函数 f(x)在(−,− )上单调递减,在(− ,+)上单调递增. a a 1 1 1 (ⅲ)当a0时，x=− , f(x)=0; x− , f(x)0；x− , f(x)0； a a a 1 1 函数 f(x)在(−,− )上单调递增,在(− ,+)上单调递减. a a …………………………………………………6分 数学参考答案与评分建议 第 5 页（共6页） {#{QQABRQKAggCIAAJAARhCAwVQCACQkBGACAoGAEAIIAAAgANABCA=}#}（2）当 a0,b0 时，函数 y = f(x) 的图像与函数 y =−be 的图像有两个交点 A(x ,y ),B(x ,y ). 1 1 2 2 (2)①当 a0,b0 时，函数 y = f(x) 的图像与函数 y =−be 的图像有两个交点 A(x ,y ),B(x ,y ), 1 1 2 2 即方程 f(x)=−eb有两个不相等的实数根x ,x ，也即曲线 f(x)=−xeax+1与直线y =−eb 1 2 1 1 有两个横坐标分别为x ,x 的交点.由（1）知,当a0时，f(x) = f(− )= ，且当x0 1 2 max a a 1 1 时， f(x)0， f(0)=0，所以0−eb ,∴− ab0. a e 1 x ②由①知当− ab0时， f(x )= f(x ),即−xeax 1 +1 =−x eax 2 +1，∴ 1 =ea(x 2 −x 1 ) ， e 1 2 1 2 x 2 x lnt tlnt 不妨设x  x 0，∴ 1 =t 1，∴t =ea(x 2 −tx 2 ),ax = ,ax = ， 1 2 x 2 1−t 1 1−t 2 1+t t−1 a(x +x )+2= (lnt−2 )， 1 2 1−t t+1 t−1 (t−1)2 令g(t)=lnt−2 ,(t 1),g(t)= 0， t+1 t(t+1)2 1+t 所以函数g(t)在(1,+)上单调递增,则g(t) g(1)=0，又t 1，∴ 0， 1−t 1+t t−1 因此a(x +x )+2= (lnt−2 )0,即a(x +x )−2. 1 2 1−t t+1 1 2 …………………………………………………12分 数学参考答案与评分建议 第 6 页（共6页） {#{QQABRQKAggCIAAJAARhCAwVQCACQkBGACAoGAEAIIAAAgANABCA=}#}