文档内容
2005 年湖南高考文科数学真题及答案
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择)题两部分,满分150分.考试用时120分钟
王新奎新疆屯敞
第Ⅰ卷(选择题)
一、选择题:本大题共10小,每小题5分,共50分.在每小题给出的四个选项中,只有一
项是符合题目要求的.
1.设全集U={-2,-1,0,1,2},A={-2,-1,0},B={0,1,2},则 =( )
A.{0} B.{-2,-1} C.{1,2} D.{0,1,2}
2.tan600°的值是( )
A. B. C. D.
3.函数f(x)= 的定义域是 (
)
A. -∞,0] B.[0,+∞ C.(-∞,0) D.(-∞,+∞)
4.如图,正方体ABCD-ABCD 的棱长为1,E是AB 的中点,则E到平面AB CD 的距离为
1 1 1 1 1 1 1 1
( )
D 1 C 1
A. B.
A B
1 E 1
C. D. D C
A B
5.已知数列 满足 ,则 = ( )
A.0 B. C. D.
6.设集合A={x| <0 ,B={x || x -1|<a ,若“a=1”是“ ”
的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分又不必要条件
7.设直线的方程是 ,从1,2,3,4,5这五个数中每次取两个不同的数作为
A、B的值,则所得不同直线的条数是 ( )
A.20 B.19 C.18 D.16
8.已知双曲线 - =1(a>0,b>0)的右焦点为F,右准线与一条渐近线交于点A,
第1页 | 共9页△OAF的面积为 (O为原点),则两条渐近线的夹角为 ( )
A.30º B.45º C.60º D.90º
9.P是△ABC所在平面上一点,若 ,则P是△ABC的( )
A.外心 B.内心 C.重心 D.垂心
10.某公司在甲、乙两地销售一种品牌车,利润(单位:万元)分别为 L=5.06x-0.15 x
1
2和L=2 x,其中x为销售量(单位:辆).若该公司在这两地共销售15辆车,则能获得的
2
最
大利润为( )
A.45.606 B.45.6 C.45.56 D.45.51
第Ⅱ卷(非选择题)
二、填空题:本大题共5小题,每小题4分(第15小题每空2分),共20分,把答案填在
答题卡中对应题号后的横线上.
11.设直线 和圆 相交于点A、B,则弦AB的垂直平分线
方程是
王新奎新疆屯敞
12.一工厂生产了某种产品16800件,它们来自甲、乙、丙3条生产线.为检查这批产品的
质量,决定采用分层抽样的方法进行抽样.已知从甲、乙、丙3条生产线抽取的个体数
组成一个等差数列,则乙生产线生产了 件产品
王新奎新疆屯敞
13.在 的展开式中,x 2项的系数是 .(用数字作
答)
14.设函数f(x)的图象关于点(1,2)对称,且存在反函数 ,f (4)=0,则
= .
15.已知平面 和直线,给出条件:① ;② ;③ ;④ ;⑤
.
(i)当满足条件 时,有 ;(ii)当满足条件 时,有
王新奎新疆屯敞
(填所选条件的序号)
三、解答题:本大题共6小题,共80分. 解答应写出文字说明,证明过程或演算步骤.
16.(本小题满分12分)
已知数列 为等差数列,且
(Ⅰ)求数列 的通项公式;
(Ⅱ)证明
第2页 | 共9页17.(本小题满分12分)
已知在△ABC中,sinA(sinB+cosB)-sinC=0,sinB+cos2C=0,求角A、B、C的
大小
王新奎新疆屯敞
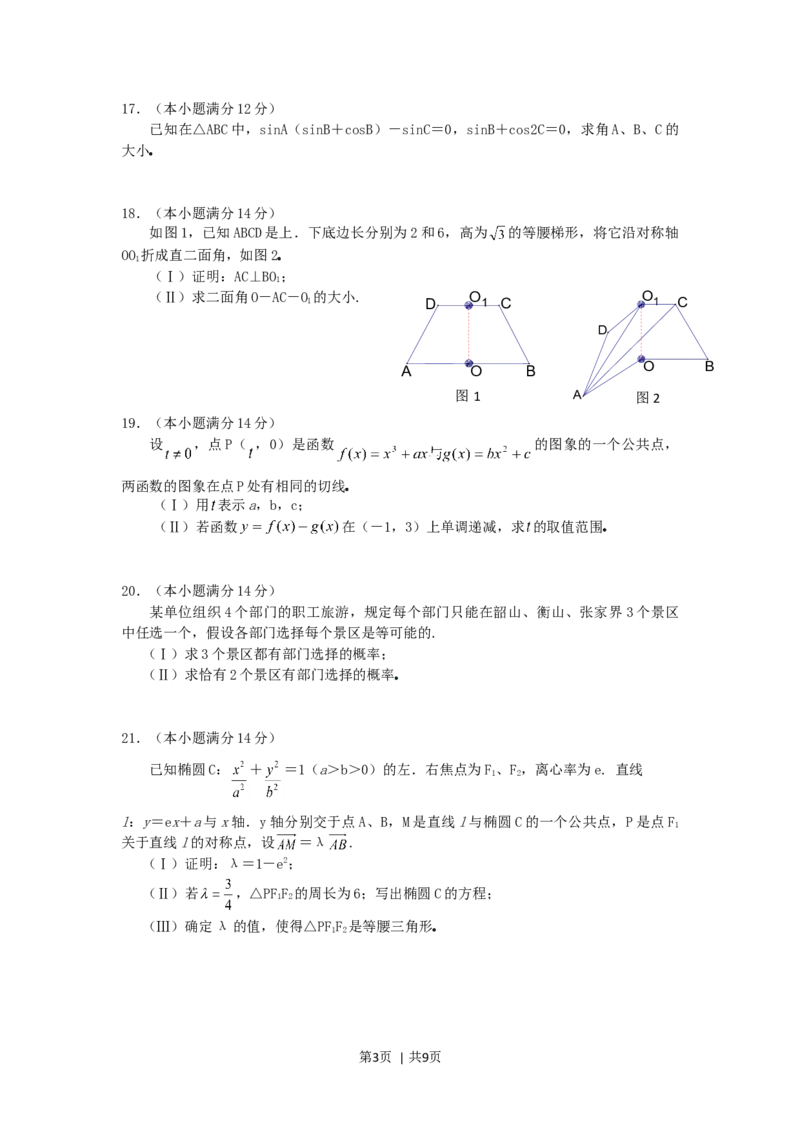
18.(本小题满分14分)
如图1,已知ABCD是上.下底边长分别为2和6,高为 的等腰梯形,将它沿对称轴
OO 折成直二面角,如图2
1 王新奎新疆屯敞
(Ⅰ)证明:AC⊥BO;
1
(Ⅱ)求二面角O-AC-O 的大小. O O
1 D 1 C 1 C
D
O B
A O B
图 1 A 图2
19.(本小题满分14分)
设 ,点P( ,0)是函数 的图象的一个公共点,
两函数的图象在点P处有相同的切线
王新奎新疆屯敞
(Ⅰ)用 表示a,b,c;
(Ⅱ)若函数 在(-1,3)上单调递减,求 的取值范围
王新奎新疆屯敞
20.(本小题满分14分)
某单位组织4个部门的职工旅游,规定每个部门只能在韶山、衡山、张家界3个景区
中任选一个,假设各部门选择每个景区是等可能的.
(Ⅰ)求3个景区都有部门选择的概率;
(Ⅱ)求恰有2个景区有部门选择的概率
王新奎新疆屯敞
21.(本小题满分14分)
已知椭圆C: + =1(a>b>0)的左.右焦点为F、F,离心率为e. 直线
1 2
l:y=ex+a与x轴.y轴分别交于点A、B,M是直线l与椭圆C的一个公共点,P是点F
1
关于直线l的对称点,设 =λ .
(Ⅰ)证明:λ=1-e2;
(Ⅱ)若 ,△PFF 的周长为6;写出椭圆C的方程;
1 2
(Ⅲ)确定λ的值,使得△PFF 是等腰三角形
1 2 王新奎新疆屯敞
第3页 | 共9页参考答案
一、选择题:1—5:CDABB 6—10: ACDDB
二、填空题:
11. 12.5600 13.35 14.-2 15.③⑤ ②⑤
三、解答题:
16.(I)解:设等差数列 的公差为d.
由 即d=1.
所以 即
(II)证明因为 ,
所以
17.解法一 由
得
所以
即
因为 所以 ,从而
由 知 从而 .
由
即
由此得 所以
解法二:由
由 、 ,所以
即
由 得
所以
即 因为 ,所以
由 从而 ,知B+2C= 不合要求.
第4页 | 共9页再由 ,得 所以
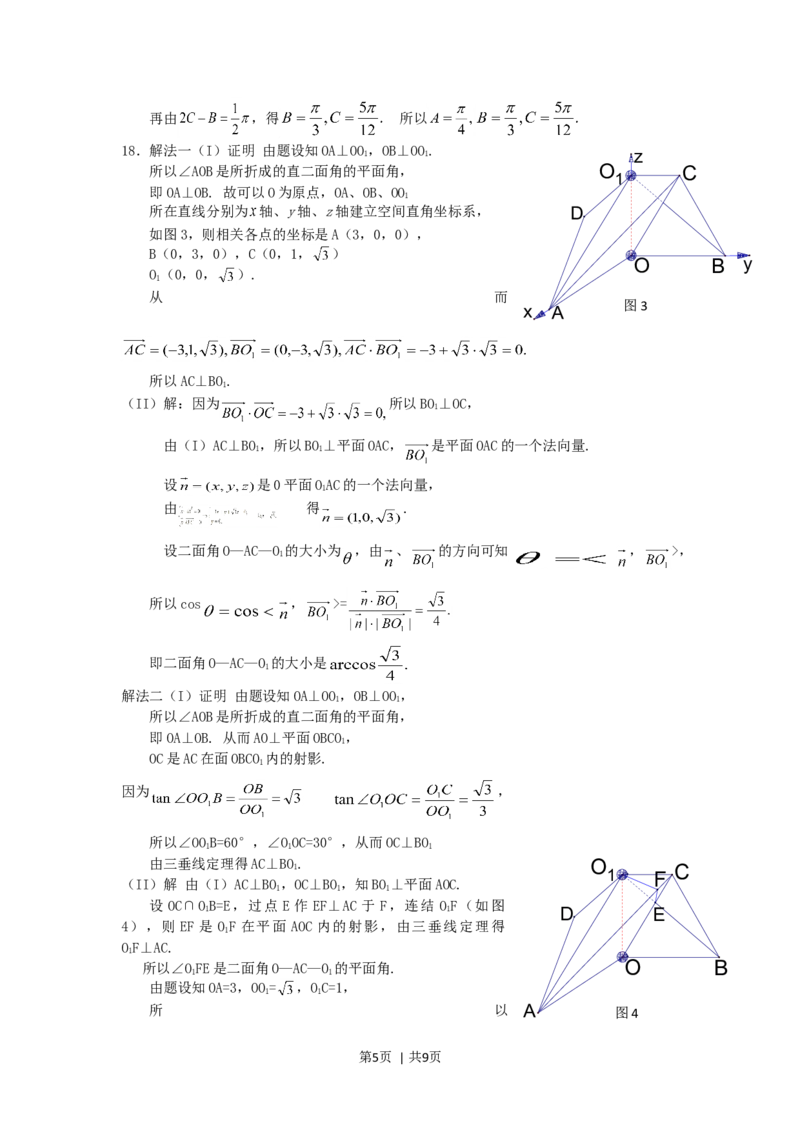
18.解法一(I)证明 由题设知OA⊥OO,OB⊥OO.
1 1 z
所以∠AOB是所折成的直二面角的平面角, O C
1
即OA⊥OB. 故可以O为原点,OA、OB、OO
1
所在直线分别为 轴、y轴、z轴建立空间直角坐标系, D
如图3,则相关各点的坐标是A(3,0,0),
B(0,3,0),C(0,1, )
O B y
O(0,0, ).
1
从 而
x A
图3
所以AC⊥BO.
1
(II)解:因为 所以BO⊥OC,
1
由(I)AC⊥BO,所以BO⊥平面OAC, 是平面OAC的一个法向量.
1 1
设 是0平面OAC的一个法向量,
1
由 得 .
设二面角O—AC—O 的大小为 ,由 、 的方向可知 , >,
1
所以cos , >=
即二面角O—AC—O 的大小是
1
解法二(I)证明 由题设知OA⊥OO,OB⊥OO,
1 1
所以∠AOB是所折成的直二面角的平面角,
即OA⊥OB. 从而AO⊥平面OBCO,
1
OC是AC在面OBCO 内的射影.
1
因为 ,
所以∠OOB=60°,∠OOC=30°,从而OC⊥BO
1 1 1
由三垂线定理得AC⊥BO. O
1 C
1 F
(II)解 由(I)AC⊥BO,OC⊥BO,知BO⊥平面AOC.
1 1 1
设 OC∩OB=E,过点 E 作 EF⊥AC 于 F,连结 OF(如图
1 1 D E
4),则 EF 是 OF 在平面 AOC 内的射影,由三垂线定理得
1
OF⊥AC.
1
所以∠OFE是二面角O—AC—O 的平面角. O B
1 1
由题设知OA=3,OO= ,OC=1,
1 1
所 以 A 图4
第5页 | 共9页,
从而 , 又OE=OO·sin30°= ,
1 1
所以 即二面角O—AC—O 的大小是
1
19.解:(I)因为函数 , 的图象都过点( ,0),所以 ,
即 .因为 所以 .
又因为 , 在点( ,0)处有相同的切线,所以
而
将 代入上式得 因此 故 , ,
(II)解法一 .
当 时,函数 单调递减.
由 ,若 ;若
由题意,函数 在(-1,3)上单调递减,则
所以
又当 时,函数 在(-1,3)上单调递减.
所以 的取值范围为
解法二:
因为函数 在(-1,3)上单调递减,且 是(-1,
3)上的抛物线,
所以 即 解得
所以 的取值范围为
20.解:某单位的4个部门选择3个景区可能出现的结果数为34.由于是任意选择,这些结
果出现的可能性都相等.
(I)3个景区都有部门选择可能出现的结果数为 (从4个部门中任选2个作为1组,
另外2个部门各作为1组,共3组,共有 种分法,每组选择不同的景区,共有
3!种选法),记“3个景区都有部门选择”为事件A,那么事件A 的概率为
1 1
第6页 | 共9页P(A)=
1
(II)解法一:分别记“恰有2个景区有部门选择”和“4个部门都选择同一个景区”为
事件A 和A,则事件A 的概率为P(A)= ,事件A 的概率为
2 3 3 3 2
P(A)=1-P(A)-P(A)=
2 1 3
解法二:恰有2个景区有部门选择可能的结果为 (先从3个景区任意选定
2个,共有 种选法,再让4个部门来选择这2个景区,分两种情况:第一种情况,
从4个部门中任取1个作为1组,另外3个部门作为1组,共2组,每组选择2个不同
的景区,共有 种不同选法.第二种情况,从4个部门中任选2个部门到1个景区
另 外 2 个 部 门 在 另 1 个 景 区 , 共 有 种 不 同 选 法 ) . 所 以 P ( A ) =
2
21.(Ⅰ)证法一:因为A、B分别是直线l: 与x轴、y轴的交点,
所以A、B的坐标分别是
王新奎新疆屯敞
所以点M的坐标是( ).
由
即 ,
证法二:因为A、B分别是直线l: 与x轴、y轴的交点,所以A、B的坐标
分别是 设M的坐标是
所以
第7页 | 共9页因为点M在椭圆上,所以
即
解得
(Ⅱ)当 时, ,所以
由△MFF的周长为6,得
1 2
所以
椭圆方程为
(Ⅲ)解法一:因为PF⊥l,所以∠PFF=90°+∠BAF 为钝角,要使△PFF 为等腰三
1 1 2 1 1 2
角形,必有|PF|=|FF|,即
1 1 2
设点F 到l的距离为d,由
1
得
所以
即当 △PFF为等腰三角形
1 2 王新奎新疆屯敞
解法二:因为PF⊥l,所以∠PFF=90°+∠BAF 为钝角,要使△PFF 为等腰三角形,
1 1 2 1 1 2
必有|PF|=|FF|,
1 1 2
设点P的坐标是 ,
则 ,
由|PF|=|FF|得
1 1 2
两边同时除以4a2,化简得
第8页 | 共9页从而
于是 . 即当 时,△PFF 为等腰三角形
1 2 王新奎新疆屯敞
第9页 | 共9页