文档内容
2006 年内蒙古高考理科数学真题及答案
一、选择题(共12小题,每小题5分,满分60分)
1.(5分)已知集合M={x|x<3},N={x|logx>1},则M∩N=( )
2
A.∅ B.{x|0<x<3} C.{x|1<x<3} D.{x|2<x<3}
2.(5分)函数y=sin2x•cos2x的最小正周期是( )
A.2π B.4π C. D.
3.(5分) =( )
A. B. C.i D.﹣i
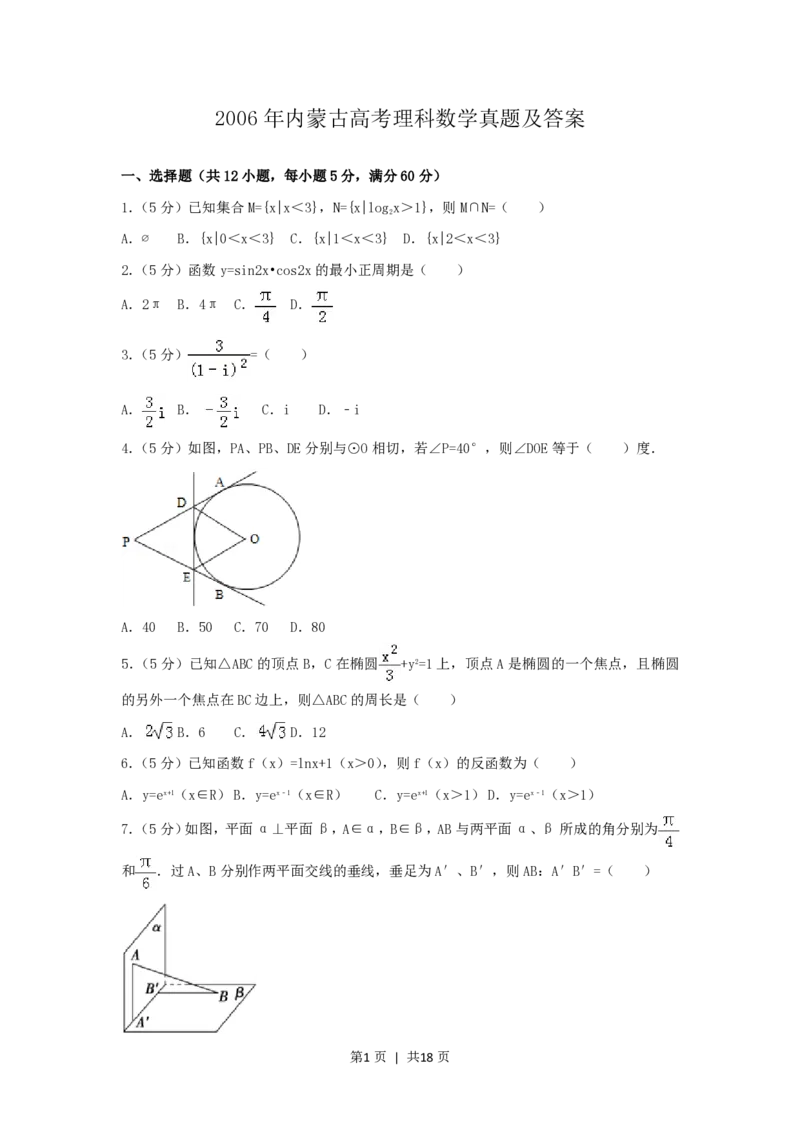
4.(5分)如图,PA、PB、DE分别与⊙O相切,若∠P=40°,则∠DOE等于( )度.
A.40 B.50 C.70 D.80
5.(5分)已知△ABC的顶点B,C在椭圆 +y2=1上,顶点A是椭圆的一个焦点,且椭圆
的另外一个焦点在BC边上,则△ABC的周长是( )
A. B.6 C. D.12
6.(5分)已知函数f(x)=lnx+1(x>0),则f(x)的反函数为( )
A.y=ex+1(x∈R)B.y=ex﹣1(x∈R) C.y=ex+1(x>1)D.y=ex﹣1(x>1)
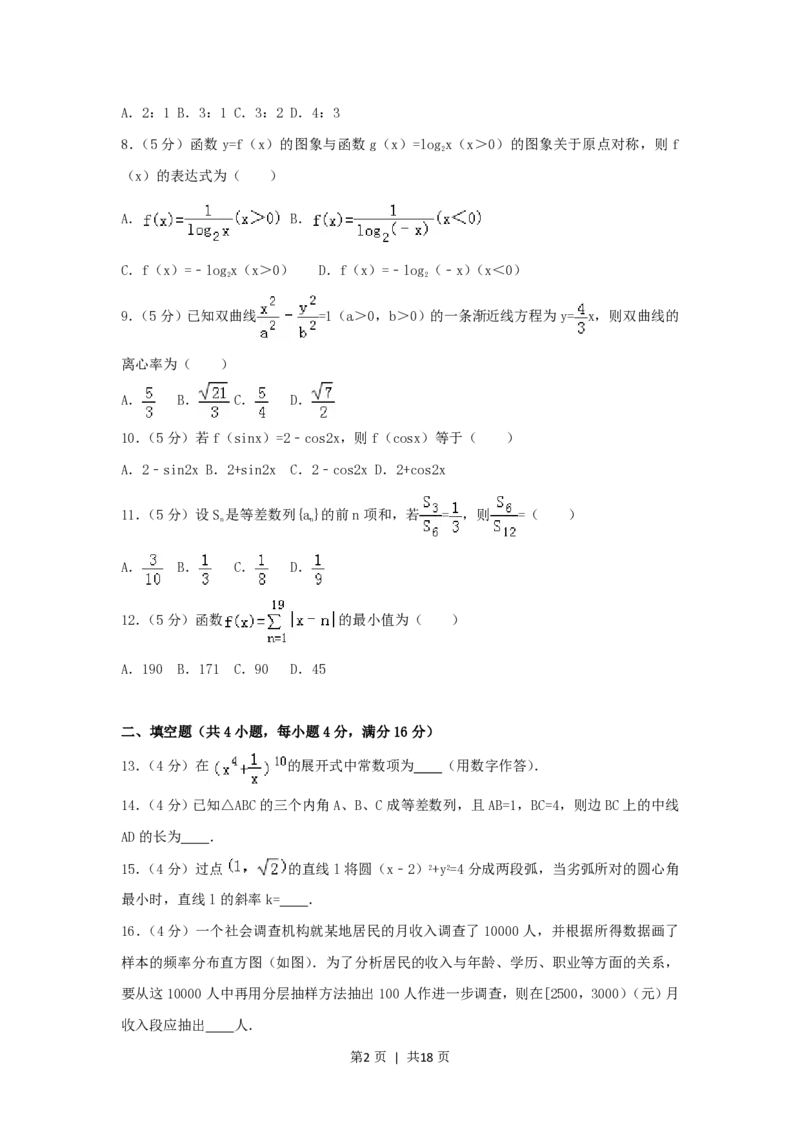
7.(5分)如图,平面α⊥平面β,A∈α,B∈β,AB与两平面α、β所成的角分别为
和 .过A、B分别作两平面交线的垂线,垂足为A′、B′,则AB:A′B′=( )
第1页 | 共18页A.2:1 B.3:1 C.3:2 D.4:3
8.(5分)函数y=f(x)的图象与函数g(x)=logx(x>0)的图象关于原点对称,则f
2
(x)的表达式为( )
A. B.
C.f(x)=﹣logx(x>0) D.f(x)=﹣log(﹣x)(x<0)
2 2
9.(5分)已知双曲线 =1(a>0,b>0)的一条渐近线方程为y= x,则双曲线的
离心率为( )
A. B. C. D.
10.(5分)若f(sinx)=2﹣cos2x,则f(cosx)等于( )
A.2﹣sin2x B.2+sin2x C.2﹣cos2x D.2+cos2x
11.(5分)设S 是等差数列{a}的前n项和,若 = ,则 =( )
n n
A. B. C. D.
12.(5分)函数 的最小值为( )
A.190 B.171 C.90 D.45
二、填空题(共4小题,每小题4分,满分16分)
13.(4分)在 的展开式中常数项为 (用数字作答).
14.(4分)已知△ABC的三个内角A、B、C成等差数列,且AB=1,BC=4,则边BC上的中线
AD的长为 .
15.(4分)过点 的直线l将圆(x﹣2)2+y2=4分成两段弧,当劣弧所对的圆心角
最小时,直线l的斜率k= .
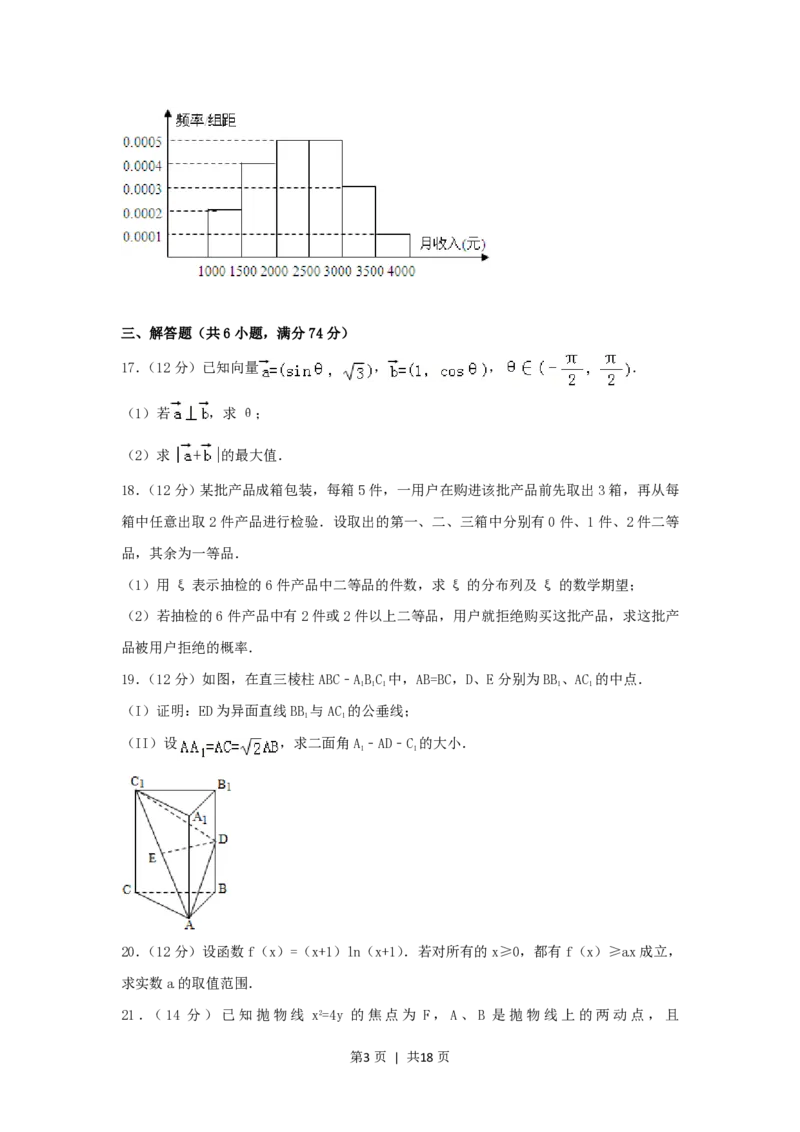
16.(4分)一个社会调查机构就某地居民的月收入调查了10000人,并根据所得数据画了
样本的频率分布直方图(如图).为了分析居民的收入与年龄、学历、职业等方面的关系,
要从这10000人中再用分层抽样方法抽出100人作进一步调查,则在[2500,3000)(元)月
收入段应抽出 人.
第2页 | 共18页三、解答题(共6小题,满分74分)
17.(12分)已知向量 , , .
(1)若 ,求θ;
(2)求 的最大值.
18.(12分)某批产品成箱包装,每箱5件,一用户在购进该批产品前先取出3箱,再从每
箱中任意出取2件产品进行检验.设取出的第一、二、三箱中分别有0件、1件、2件二等
品,其余为一等品.
(1)用ξ表示抽检的6件产品中二等品的件数,求ξ的分布列及ξ的数学期望;
(2)若抽检的6件产品中有2件或2件以上二等品,用户就拒绝购买这批产品,求这批产
品被用户拒绝的概率.
19.(12分)如图,在直三棱柱ABC﹣ABC 中,AB=BC,D、E分别为BB、AC 的中点.
1 1 1 1 1
(I)证明:ED为异面直线BB 与AC 的公垂线;
1 1
(II)设 ,求二面角A﹣AD﹣C 的大小.
1 1
20.(12分)设函数f(x)=(x+1)ln(x+1).若对所有的x≥0,都有f(x)≥ax成立,
求实数a的取值范围.
21.(14 分)已知抛物线 x2=4y 的焦点为 F,A、B 是抛物线上的两动点,且
第3页 | 共18页.过A、B两点分别作抛物线的切线,设其交点为M.
(Ⅰ)证明 为定值;
(Ⅱ)设△ABM的面积为S,写出S=f(λ)的表达式,并求S的最小值.
22.(12分)设数列{a}的前n项和为S,且方程x2﹣ax﹣a=0有一根为S﹣1,n=1,2,
n n n n n
3,….
(1)求a,a;
1 2
(2)猜想数列{S}的通项公式,并给出严格的证明.
n
2006年内蒙古高考理科数学真题参考答案
一、选择题(共12小题,每小题5分,满分60分)
1.(5分)已知集合M={x|x<3},N={x|logx>1},则M∩N=( )
2
A.∅ B.{x|0<x<3} C.{x|1<x<3} D.{x|2<x<3}
【分析】解出集合N,结合数轴求交集.
【解答】解:N={x|logx>1}={x|x>2},
2
用数轴表示可得答案D
故选D.
2.(5分)函数y=sin2x•cos2x的最小正周期是( )
A.2π B.4π C. D.
【分析】将函数化简为:y=Asin(ωx+φ)的形式即可得到答案.
【解答】解: 所以最小正周期为 ,
故选D
3.(5分) =( )
第4页 | 共18页A. B. C.i D.﹣i
【分析】化简复数的分母,再分子、分母同乘分母的共轭复数,化简即可.
【解答】解:
故选A.
4.(5分)如图,PA、PB、DE分别与⊙O相切,若∠P=40°,则∠DOE等于( )度.
A.40 B.50 C.70 D.80
【分析】连接OA、OB、OP,由切线的性质得∠AOB=140°,再由切线长定理求得∠DOE的度
数.
【解答】解:连接OA、OB、OP,
∵∠P=40°,
∴∠AOB=140°,
∵PA、PB、DE分别与⊙O相切,
∴∠AOD=∠POD,∠BOE=∠POE,
∴∠DOE= ∠AOB= ×140°=70°.
故选C.
5.(5分)已知△ABC的顶点B,C在椭圆 +y2=1上,顶点A是椭圆的一个焦点,且椭圆
第5页 | 共18页的另外一个焦点在BC边上,则△ABC的周长是( )
A. B.6 C. D.12
【分析】由椭圆的定义:椭圆上一点到两焦点的距离之和等于长轴长2a,可得△ABC的周
长.
【解答】解:由椭圆的定义:椭圆上一点到两焦点的距离之和等于长轴长2a,
可得△ABC的周长为4a= ,
故选C
6.(5分)已知函数f(x)=lnx+1(x>0),则f(x)的反函数为( )
A.y=ex+1(x∈R)B.y=ex﹣1(x∈R) C.y=ex+1(x>1)D.y=ex﹣1(x>1)
【分析】本题考查反函数的概念、求反函数的方法、指数式与对数式的互化,求函数的值域;
将y=lnx+1看做方程解出x,然后由原函数的值域确定反函数的定义域即可.
【解答】解:由y=lnx+1解得x=ey﹣1,即:y=ex﹣1
∵x>0,∴y∈R
所以函数f(x)=lnx+1(x>0)反函数为y=ex﹣1(x∈R)
故选B
7.(5分)如图,平面α⊥平面β,A∈α,B∈β,AB与两平面α、β所成的角分别为
和 .过A、B分别作两平面交线的垂线,垂足为A′、B′,则AB:A′B′=( )
A.2:1 B.3:1 C.3:2 D.4:3
【分析】设AB的长度为a用a表示出A'B'的长度,即可得到两线段的比值.
【解答】解:连接AB'和A'B,设AB=a,可得AB与平面α所成的角为 ,
在Rt△BAB'中有AB'= ,同理可得AB与平面β所成的角为 ,
第6页 | 共18页所以 ,因此在Rt△AA'B'中A'B'= ,
所以AB:A'B'= ,
故选A.
8.(5分)函数y=f(x)的图象与函数g(x)=logx(x>0)的图象关于原点对称,则f
2
(x)的表达式为( )
A. B.
C.f(x)=﹣logx(x>0) D.f(x)=﹣log(﹣x)(x<0)
2 2
【分析】先设函数f(x)上的点为(x,y),根据(x,y)关于原点的对称点为(﹣x,
﹣y)且函数y=f(x)的图象与函数g(x)=logx(x>0)的图象关于原点对称,得到x与
2
y的关系式,即得答案.
【解答】解:设(x,y)在函数f(x)的图象上
∵(x,y)关于原点的对称点为(﹣x,﹣y),
所以(﹣x,﹣y)在函数g(x)上
∴﹣y=log(﹣x)⇒f(x)=﹣log(﹣x)(x<0)
2 2
故选D.
9.(5分)已知双曲线 =1(a>0,b>0)的一条渐近线方程为y= x,则双曲线的
离心率为( )
A. B. C. D.
【分析】由题意设出双曲线的方程,得到它的一条渐近线方程y= x即y= x,由此可得b:
a=4:3,结合双曲线的平方关系可得c与a的比值,求出该双曲线的离心率.
【解答】解:∵双曲线的中心在原点,焦点在x轴上,
∴设双曲线的方程为 ,(a>0,b>0)
第7页 | 共18页由此可得双曲线的渐近线方程为y=± x,结合题意一条渐近线方程为y= x,
得 = ,设b=4t,a=3t,则c= =5t(t>0)
∴该双曲线的离心率是e= = .
故选A.
10.(5分)若f(sinx)=2﹣cos2x,则f(cosx)等于( )
A.2﹣sin2x B.2+sin2x C.2﹣cos2x D.2+cos2x
【分析】本题考查的知识点是函数解析式的求法,根据已知中f(sinx)=2﹣cos2x,结合
倍角公式对解析式进行凑配,不难得到函数f(x)的解析式,然后将cosx代入,并化简即
可得到答案.
【解答】解:∵f(sinx)=2﹣(1﹣2sin2x)=1+2sin2x,
∴f(x)=1+2x2,(﹣1≤x≤1)
∴f(cosx)=1+2cos2x=2+cos2x.
故选D
11.(5分)设S 是等差数列{a}的前n项和,若 = ,则 =( )
n n
A. B. C. D.
【分析】根据等差数列的前n项和公式,用a 和d分别表示出s 与s,代入 中,整
1 3 6
理得a=2d,再代入 中化简求值即可.
1
【解答】解:设等差数列{a}的首项为a,公差为d,
n 1
由等差数列的求和公式可得 且d≠0,
∴ ,
故选A.
第8页 | 共18页12.(5分)函数 的最小值为( )
A.190 B.171 C.90 D.45
【分析】利用绝对值的几何意义求解或者绝对值不等式的性质求解.
【解答】解法一:f(x)= =|x﹣1|+|x﹣2|+|x﹣3|+|x﹣19|表示数轴上一点到
1,2,3,…,19的距离之和,
可知x在1﹣19最中间时f(x)取最小值.即x=10时f(x)有最小值90,
故选C.
解法二:|x﹣1|+|x﹣19|≥18,当1≤x≤19时取等号;
|x﹣2|+|x﹣18|≥16,当2≤x≤18时取等号;
|x﹣3|+|x﹣17|≥14,当3≤x≤17时取等号;
…
|x﹣9|+|x﹣11|≥2,当9≤x≤11时取等号;
|x﹣10|≥0,当x=10时取等号;
将上述所有不等式累加得|x﹣1|+|x﹣2|+|x﹣3|+…+|x﹣19|≥18+16+14+…+2+0=90(当且
仅当x=10时取得最小值)
故选C.
二、填空题(共4小题,每小题4分,满分16分)
13.(4分)在 的展开式中常数项为 45 (用数字作答).
【分析】利用二项式的通项公式(让次数为0,求出r)就可求出答案.
【解答】解: 要求常数项,
即40﹣5r=0,
可得r=8代入通项公式可得T =C 8=C 2=45
r+1 10 10
故答案为:45.
14.(4分)已知△ABC的三个内角A、B、C成等差数列,且AB=1,BC=4,则边BC上的中线
第9页 | 共18页AD的长为 .
【分析】先根据三个内角A、B、C成等差数列和三角形内角和为π可求得B的值,进而利
用AD为边BC上的中线求得BD,最后在△ABD中利用余弦定理求得AD.
【解答】解:∵△ABC的三个内角A、B、C成等差数列
∴A+C=2B
∵A+B+C=π
∴
∵AD为边BC上的中线
∴BD=2,
由余弦定理定理可得
故答案为:
15.(4分)过点 的直线l将圆(x﹣2)2+y2=4分成两段弧,当劣弧所对的圆心角
最小时,直线l的斜率k= .
【分析】本题考查的是直线垂直时斜率之间的关系,及直线与圆的相关性质,要处理本题我
们先要画出满足条件的图形,数形结合容易得到符合题目中的条件的数理关系,由劣弧所对
的圆心角最小弦长最短,及过圆内一点最短的弦与过该点的直径垂直,易得到解题思路.
【解答】解:如图示,由图形可知:
点A 在圆(x﹣2)2+y2=4的内部,
圆心为O(2,0)要使得劣弧所对的圆心角最小,
只能是直线l⊥OA,
所以 .
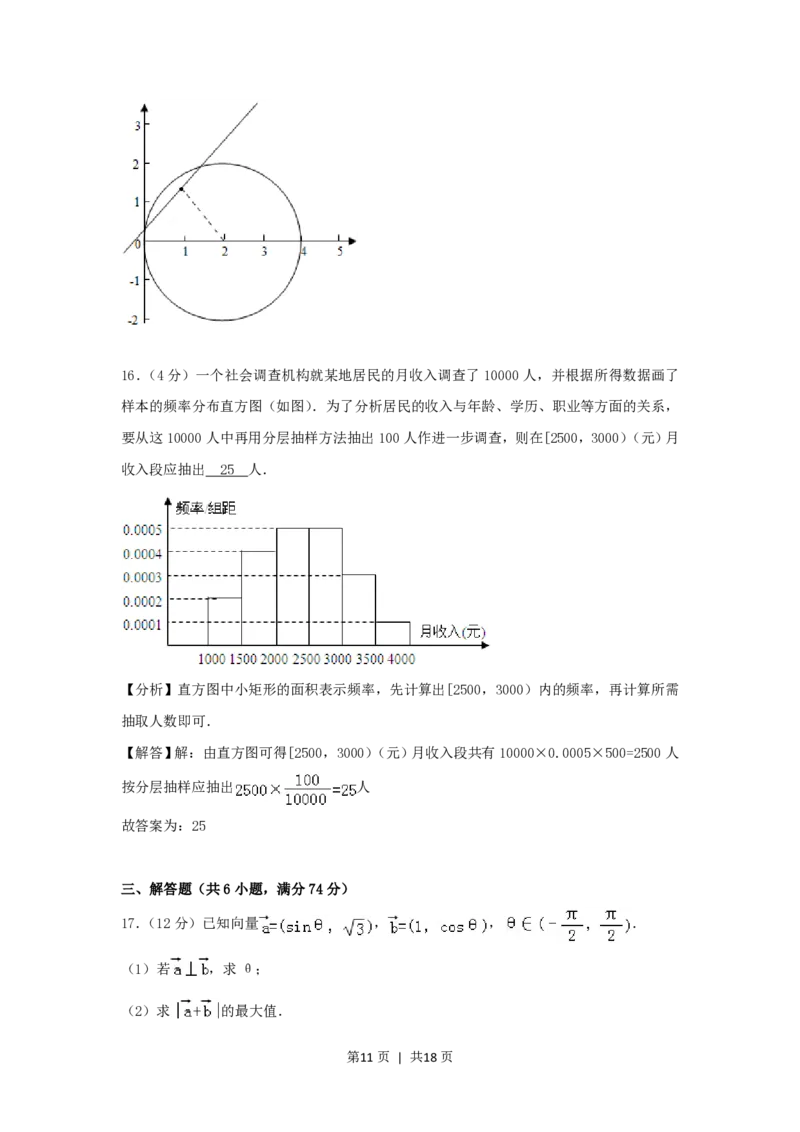
第10页 | 共18页16.(4分)一个社会调查机构就某地居民的月收入调查了10000人,并根据所得数据画了
样本的频率分布直方图(如图).为了分析居民的收入与年龄、学历、职业等方面的关系,
要从这10000人中再用分层抽样方法抽出100人作进一步调查,则在[2500,3000)(元)月
收入段应抽出 25 人.
【分析】直方图中小矩形的面积表示频率,先计算出[2500,3000)内的频率,再计算所需
抽取人数即可.
【解答】解:由直方图可得[2500,3000)(元)月收入段共有10000×0.0005×500=2500人
按分层抽样应抽出 人
故答案为:25
三、解答题(共6小题,满分74分)
17.(12分)已知向量 , , .
(1)若 ,求θ;
(2)求 的最大值.
第11页 | 共18页【分析】(1)利用向量垂直的充要条件列出方程,利用三角函数的商数关系求出正切,求出
角.
(2)利用向量模的平方等于向量的平方,利用三角函数的平方关系及公式
,化简 ,利用三角函数的有界性求出范
围.
【解答】解:(1)因为 ,所以
得
又 ,
所以θ=
(2)因为
=
所以当θ= 时, 的最大值为5+4=9
故 的最大值为3
18.(12分)某批产品成箱包装,每箱5件,一用户在购进该批产品前先取出3箱,再从每
箱中任意出取2件产品进行检验.设取出的第一、二、三箱中分别有0件、1件、2件二等
品,其余为一等品.
(1)用ξ表示抽检的6件产品中二等品的件数,求ξ的分布列及ξ的数学期望;
(2)若抽检的6件产品中有2件或2件以上二等品,用户就拒绝购买这批产品,求这批产
品被用户拒绝的概率.
【分析】(1)由取出的第一、二、三箱中分别有0件、1件、2件二等品可知变量ξ的取值,
结合变量对应的事件做出这四个事件发生的概率,写出分布列和期望.
(2)由上一问做出的分布列可以知道,P(ξ=2)= ,P(ξ=3)= ,这两个事件是互
斥的,根据互斥事件的概率公式得到结果.
【解答】解(1)由题意知抽检的6件产品中二等品的件数ξ=0,1,2,3
第12页 | 共18页=
= ,
∴ξ的分布列为
ξ 0 1 2 3
P
∴ξ的数学期望E(ξ)=
(2)∵P(ξ=2)= ,P(ξ=3)= ,这两个事件是互斥的
∴P(ξ≥2)=
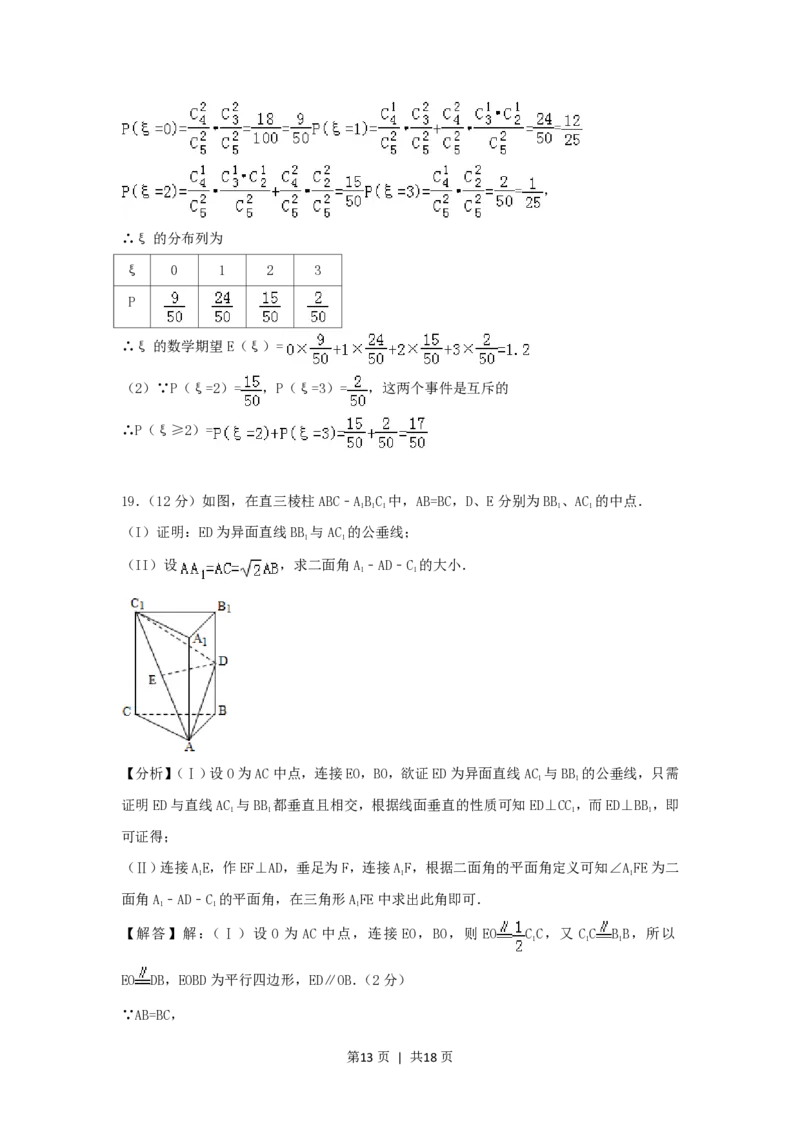
19.(12分)如图,在直三棱柱ABC﹣ABC 中,AB=BC,D、E分别为BB、AC 的中点.
1 1 1 1 1
(I)证明:ED为异面直线BB 与AC 的公垂线;
1 1
(II)设 ,求二面角A﹣AD﹣C 的大小.
1 1
【分析】(Ⅰ)设O为AC中点,连接EO,BO,欲证ED为异面直线AC 与BB 的公垂线,只需
1 1
证明ED与直线AC 与BB 都垂直且相交,根据线面垂直的性质可知ED⊥CC,而ED⊥BB,即
1 1 1 1
可证得;
(Ⅱ)连接AE,作EF⊥AD,垂足为F,连接AF,根据二面角的平面角定义可知∠AFE为二
1 1 1
面角A﹣AD﹣C 的平面角,在三角形AFE中求出此角即可.
1 1 1
【解答】解:(Ⅰ)设 O 为 AC 中点,连接 EO,BO,则 EO CC,又 CC BB,所以
1 1 1
EO DB,EOBD为平行四边形,ED∥OB.(2分)
∵AB=BC,
第13页 | 共18页∴BO⊥AC,
又平面ABC⊥平面ACCA,BOÌ面ABC,
1 1
故BO⊥平面ACCA,
1 1
∴ED⊥平面ACCA,ED⊥AC,ED⊥CC,
1 1 1 1
∴ED⊥BB,ED为异面直线AC 与BB 的公垂线.(6分)
1 1 1
(Ⅱ)连接AE,由AA=AC= AB可知,AACC 为正方形,
1 1 1 1
∴AE⊥AC,又由ED⊥平面ACCA 和EDÌ平面ADC 知平面
1 1 1 1 1
ADC⊥平面AACC,
1 1 1
∴AE⊥平面ADC.
1 1
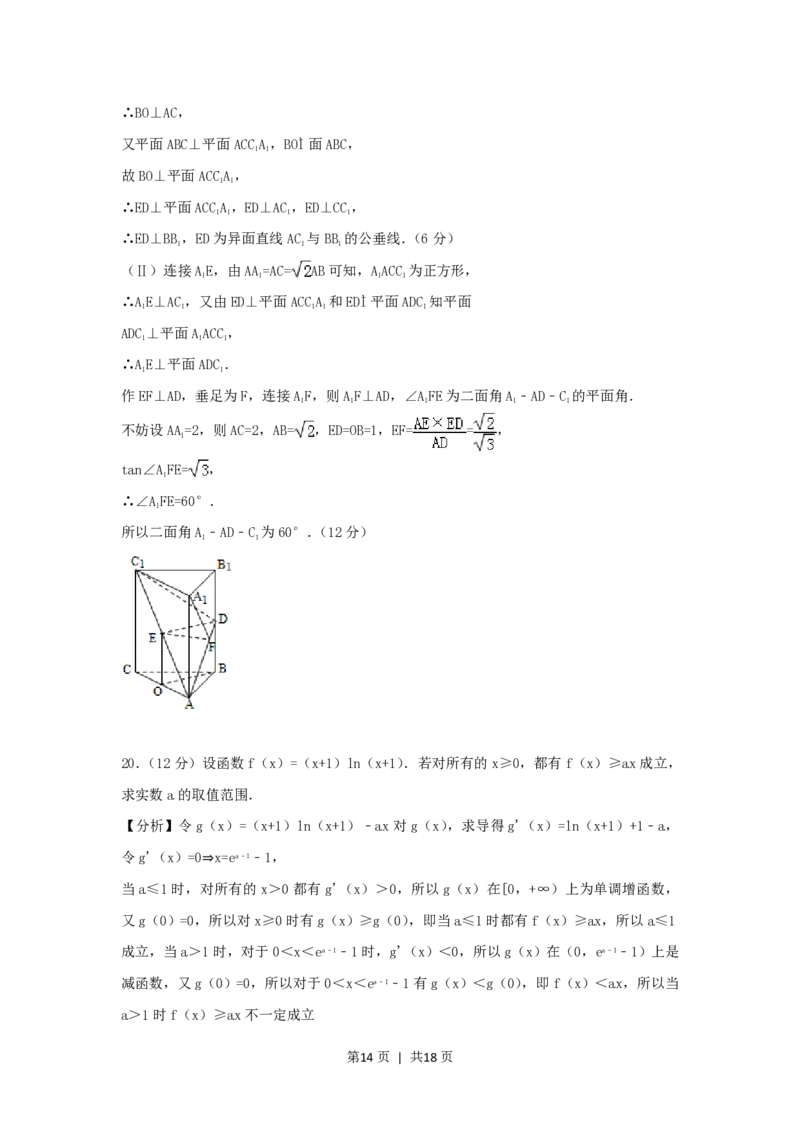
作EF⊥AD,垂足为F,连接AF,则AF⊥AD,∠AFE为二面角A﹣AD﹣C 的平面角.
1 1 1 1 1
不妨设AA=2,则AC=2,AB= ,ED=OB=1,EF= = ,
1
tan∠AFE= ,
1
∴∠AFE=60°.
1
所以二面角A﹣AD﹣C 为60°.(12分)
1 1
20.(12分)设函数f(x)=(x+1)ln(x+1).若对所有的x≥0,都有f(x)≥ax成立,
求实数a的取值范围.
【分析】令g(x)=(x+1)ln(x+1)﹣ax对g(x),求导得g'(x)=ln(x+1)+1﹣a,
令g'(x)=0⇒x=ea﹣1﹣1,
当a≤1时,对所有的x>0都有g'(x)>0,所以g(x)在[0,+∞)上为单调增函数,
又g(0)=0,所以对x≥0时有g(x)≥g(0),即当a≤1时都有f(x)≥ax,所以a≤1
成立,当a>1时,对于0<x<ea﹣1﹣1时,g'(x)<0,所以g(x)在(0,ea﹣1﹣1)上是
减函数,又g(0)=0,所以对于0<x<ea﹣1﹣1有g(x)<g(0),即f(x)<ax,所以当
a>1时f(x)≥ax不一定成立
第14页 | 共18页综上所述即可得出a的取值范围.
【解答】解法一:
令g(x)=(x+1)ln(x+1)﹣ax,
对函数g(x)求导数:g′(x)=ln(x+1)+1﹣a
令g′(x)=0,解得x=ea﹣1﹣1,
(i)当a≤1时,对所有x>0,g′(x)>0,所以g(x)在[0,+∞)上是增函数,
又g(0)=0,所以对x≥0,都有g(x)≥g(0),
即当a≤1时,对于所有x≥0,都有f(x)≥ax.
(ii)当a>1时,对于0<x<ea﹣1﹣1,g′(x)<0,所以g(x)在(0,ea﹣1﹣1)是减
函数,
又g(0)=0,所以对0<x<ea﹣1﹣1,都有g(x)<g(0),
即当a>1时,不是对所有的x≥0,都有f(x)≥ax成立.
综上,a的取值范围是(﹣∞,1].
解法二:
令g(x)=(x+1)ln(x+1)﹣ax,
于是不等式f(x)≥ax成立即为g(x)≥g(0)成立.
对函数g(x)求导数:g′(x)=ln(x+1)+1﹣a
令g′(x)=0,解得x=ea﹣1﹣1,
当x>ea﹣1﹣1时,g′(x)>0,g(x)为增函数,
当﹣1<x<ea﹣1﹣1,g′(x)<0,g(x)为减函数,
所以要对所有x≥0都有g(x)≥g(0)充要条件为ea﹣1﹣1≤0.
由此得a≤1,即a的取值范围是(﹣∞,1].
21.(14 分)已知抛物线 x2=4y 的焦点为 F,A、B 是抛物线上的两动点,且
.过A、B两点分别作抛物线的切线,设其交点为M.
(Ⅰ)证明 为定值;
(Ⅱ)设△ABM的面积为S,写出S=f(λ)的表达式,并求S的最小值.
【分析】(1)设A(x,y),B(x,y),M(x,y),根据抛物线方程可得焦点坐标和准线
1 1 2 2 o o
方程,设直线方程与抛物线方程联立消去y,根据判别式大于0求得x+x 和xx,根据曲线
1 2 1 2
第15页 | 共18页4y=x2上任意一点斜率为y′= ,可得切线AM和BM的方程,联立方程求得交点坐标,求得
和 ,进而可求得 • 的结果为0,进而判断出AB⊥FM.
(2)利用(1)的结论,根据x+x 的关系式求得k和λ的关系式,进而求得弦长AB,可
1 2
表示出△ABM面积.最后根据均值不等式求得S的范围,得到最小值.
【解答】解:(1)设A(x ,y ),B(x ,y ),M(x ,y ),焦点F(0,1),准线方程为
1 1 2 2 o o
y=﹣1,
显然AB斜率存在且过F(0,1)
设其直线方程为y=kx+1,联立4y=x2消去y得:x2﹣4kx﹣4=0,
判别式△=16(k2+1)>0.
x+x=4k,xx=﹣4
1 2 1 2
于是曲线4y=x2上任意一点斜率为y′= ,则易得切线AM,BM方程分别为y=( )x(x﹣x)
1 1
+y ,y=( )x (x﹣x )+y ,其中 4y=x2,4y=x2,联立方程易解得交点 M 坐标,
1 2 2 2 1 1 2 2
x= =2k,y= =﹣1,即M( ,﹣1)
o o
从而, =( ,﹣2), (x﹣x,y﹣y)
2 1 2 1
• = (x+x)(x﹣x)﹣2(y﹣y)= (x2﹣x2)﹣2[ (x2﹣x2)]=0,(定值)命
1 2 2 1 2 1 2 1 2 1
题得证.
这就说明AB⊥FM.
(Ⅱ)由(Ⅰ)知在△ABM中,FM⊥AB,因而S= |AB||FM|.
∵ ,
∴(﹣x,1﹣y)=λ(x,y﹣1),即 ,
1 1 2 2
而4y=x2,4y=x2,
1 1 2 2
则x2= ,x2=4λ,
2 1
|FM|= = = = .
因为|AF|、|BF|分别等于A、B到抛物线准线y=﹣1的距离,所以
第16页 | 共18页|AB|=|AF|+|BF|=y+y+2= +2=λ+ +2=( )2.
1 2
于是S= |AB||FM|= ( )3,
由 ≥2知S≥4,且当λ=1时,S取得最小值4.
22.(12分)设数列{a}的前n项和为S,且方程x2﹣ax﹣a=0有一根为S﹣1,n=1,2,
n n n n n
3,….
(1)求a,a;
1 2
(2)猜想数列{S}的通项公式,并给出严格的证明.
n
【分析】(1)验证当n=1时,x2﹣ax﹣a=0有一根为a 根据根的定义,可求得a,同理,
1 1 1 1
当n=2时,也可求得a;
2
(2)用数学归纳法证明数列问题时分为两个步骤,第一步,先证明当当n=1时,已知结论
成立,第二步,先假设n=k时结论成立,利用此假设结合题设条件证明当n=k+1时,结论也
成立即可.
【解答】解:(1)当n=1时,x2﹣ax﹣a=0有一根为S﹣1=a﹣1,
1 1 1 1
于是(a﹣1)2﹣a(a﹣1)﹣a=0,解得a= .
1 1 1 1 1
当n=2时,x2﹣ax﹣a=0有一根为S﹣1=a﹣ ,
2 2 2 2
于是(a﹣ )2﹣a(a﹣ )﹣a=0,
2 2 2 2
解得a= .
2
(2)由题设(S﹣1)2﹣a(S﹣1)﹣a=0,
n n n n
S2﹣2S+1﹣aS=0.
n n n n
当n≥2时,a=S﹣S ,
n n n﹣1
代入上式得S S﹣2S+1=0.①
n﹣1 n n
由(1)得S=a= ,S=a+a= + = .
1 1 2 1 2
由①可得S= .由此猜想S= ,n=1,2,3,.
3 n
下面用数学归纳法证明这个结论.
(i)n=1时已知结论成立.
第17页 | 共18页(ii)假设n=k时结论成立,即S= ,当n=k+1时,由①得S = ,即S = ,
k k+1 k+1
故n=k+1时结论也成立.
综上,由(i)、(ii)可知S= 对所有正整数n都成立.
n
第18页 | 共18页