河南省洛阳市第一高级中学2025-2026学年高二上学期1月月考数学试卷（含解析）_2024-2025高二（7-7月题库）_2026年1月高二_260114河南省洛阳市第一高级中学2025-2026学年高二上学期1月月考

洛阳一高 2024 级 1 月月考数学试卷 2026.1.7 一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项 是符合题目要求的． 1.已知直线 与 垂直，则实数 的值为 A. B. 或 C. D. 或 2.若等比数列 满足 ， ，则数列 的公比等于 A. 或 B. 或 C. D. 3.点 到直线 的距离的最大值为 A. B. C. D. 4.已知数列 满足 ， ，则 A. B. C. D. 5.方程 表示的曲线为 A.两个半圆 B.一个圆 C.半个圆 D.两个圆 6.在正方体 中， 为 的中点，则直线 与 所成的角为 A. B. C. D. 7.设点 ，若在圆 上存在点 ，使 ，则 的取值范围为A. B. C. D. 8.已知 ， 在 上，则 的面积 有最大值，但没有最小值 没有最大值，但有最小值 既有最大值，也有最小值 既没有最大值，也没有最小值 二、选择题：本题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题 目要求．全部选对的得6分，部分选对的得部分分，有选错的得0分． 9.已知实数 满足方程 ，则 A. 的最大值为 B. 的最小值为 C. 的最大值为 D. 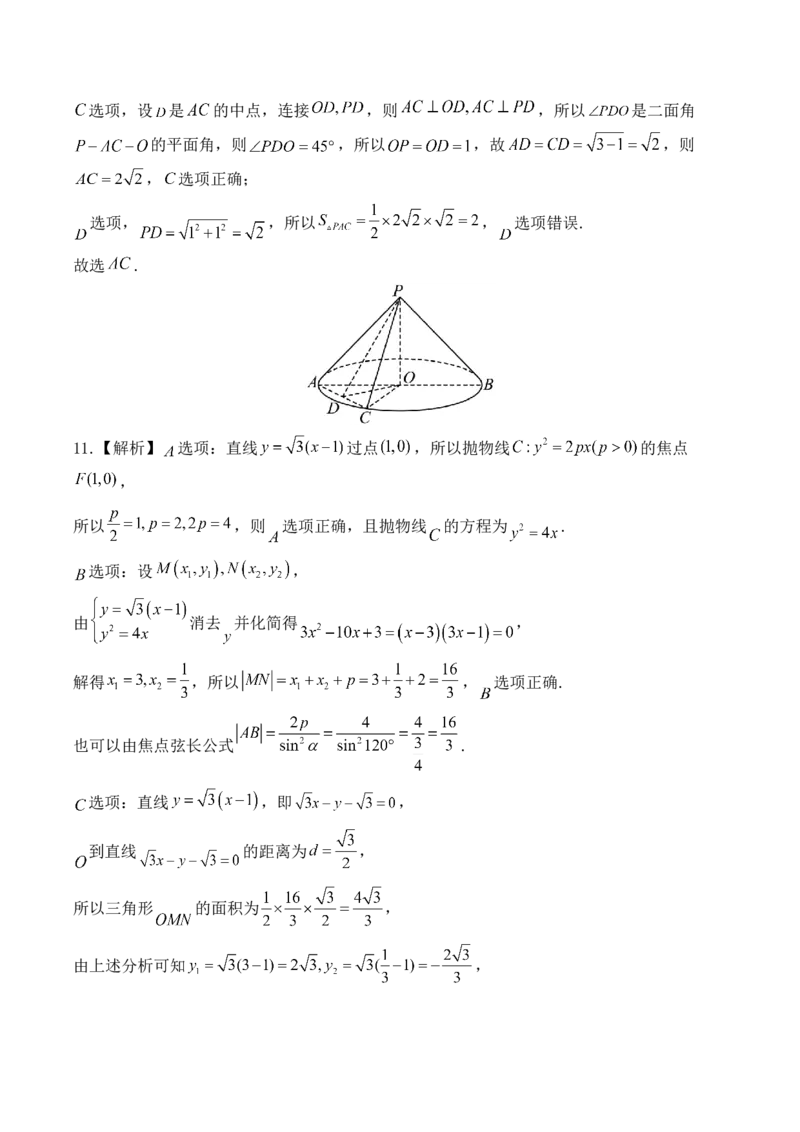的最小值为 10.已知圆锥的顶点为 ，底面圆心为 ， 为底面直径， ， ，点 在 底面圆周上，且二面角 为 ，则 该圆锥的体积为 该圆锥的侧面积为 的面积为 11.设 为坐标原点，直线 过抛物线 的焦点，且与 交于 两点， 为 的准线，则 为等腰三角形 以 为直径的圆与 相切 三、填空题：本题共3小题，每小题5分，共15分． 12.已知递增的等比数列 前 项和为 ，且 ，则数列 的前 10项和为__________.ABCABC 13.直三棱柱 1 1 1的各顶点都在同一球面上，若 ， ， 则此球的表面积等于___________. x2 y2  1 P(i 1,23, 14.设 F 是椭圆 7 6 的右焦点，且椭圆上至少有 21 个不同的点 i …)，使 |FP |,|FP |,|FP | 1 2 3 ，…，组成公差为d 的等差数列，则d 的取值范围为_________. 四、解答题：本题共5小题，共77分．解答应写出文字说明、证明过程或演算步骤． 15.(13分)设抛物线 ， 为坐标原点，点 ，过点 的直线 与 交于 两点． (1)证明： ； (2)证明： ． 16.(15分)记 为数列 的前 项和．已知 ． (1)证明： 是等差数列； (2)若 成等比数列，求 的最小值． 17.(15分)如图，在四棱锥 中，侧面 平面 ， 是边长为2的等边 三角形，底面 为直角梯形，其中 ．(1)求证： ． (2)线段 上是否存在一点 ，使得平面 与平面 夹角的余弦值为 ？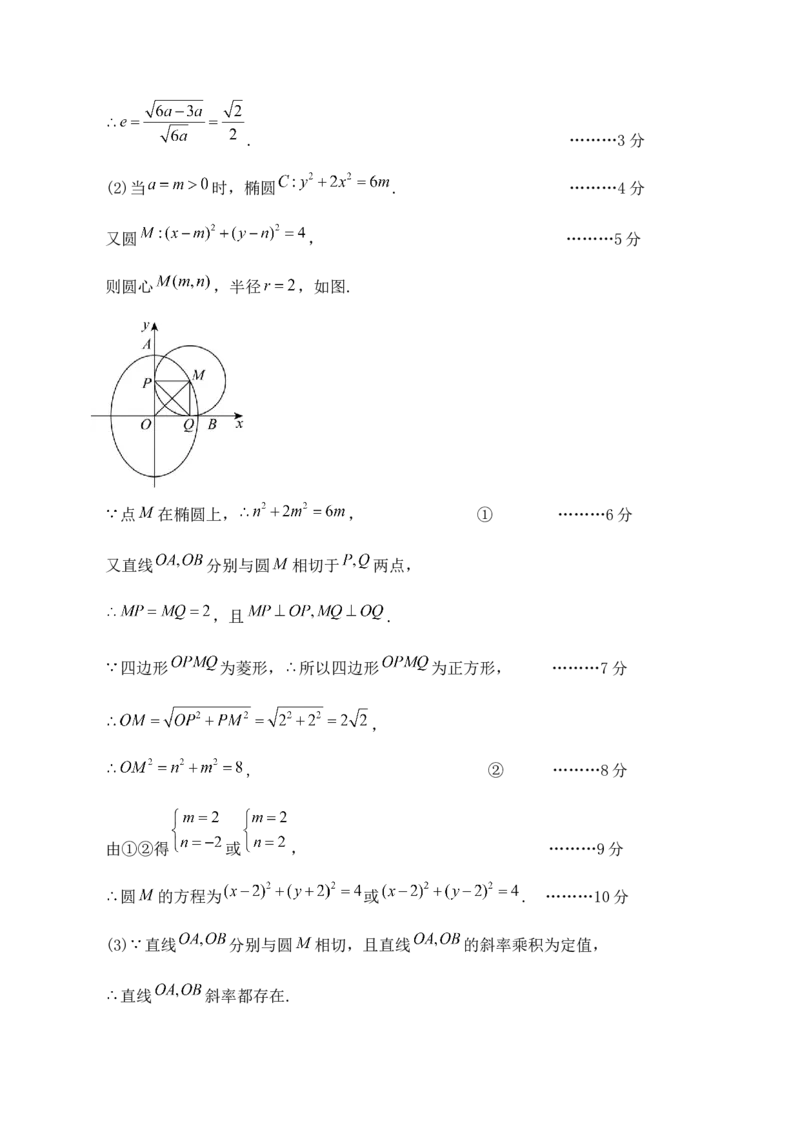若 存在，求出 的值；若不存在，请说明理由． 18.(17分)某牧场今年初牛的存栏数为1200，预计以后每年存栏数的增长率为8%，且在每年 c c c 年底卖出100头牛．设牧场从今年起每年年初的计划存栏数依次为 1， 2， 3，…． c c (1)写出一个递推公式，表示 n1与 n之间的关系； c k  r(c k) k,r (2)将(1)中的递推公式表示成 n1 n 的形式，其中 为常数； S c c c  c (3)求 10 1 2 3  10的值（精确到1）． ( ) 19.(17分)已知椭圆 ，圆 ，点 均在椭圆 上， 为坐标原点，直线 分别与圆 相切于 两点． (1)求椭圆的离心率； (2)当 ，四边形 为菱形时，求圆 的方程； (3)若直线 的斜率乘积为定值，求 的值．题号 1 2 3 4 5 6 7 8 9 10 11 答案 1 1 [ ,0) (0, ]  12. 13. 14. 10 10 1.【解析】 ，则 ，解得 或 . 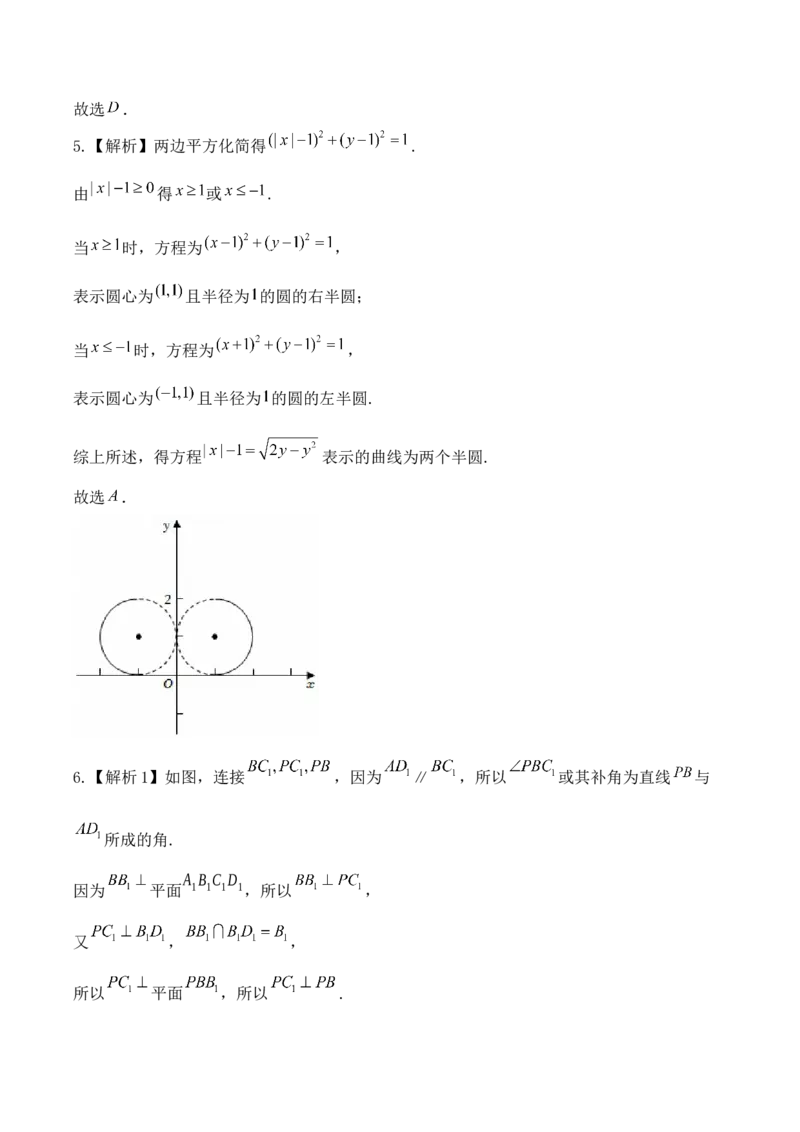故选 ． 2.【解析】因为等比数列 满足 ， ， 设公比为 ，可得 且 ，解得 ． 故选 ． 3.【解析】直线 表示经过点 ，且斜率为 的直线， 根据点到直线的距离的定义，可知 时，点 到直线 的距离等于 ，达到最大值． 故选 ． 4.【解析】因为 ， ， 所以 ，得 ； 由 ，得 ； 由 ，得 ； 由 ，得 ．故选 ． 5.【解析】两边平方化简得 . 由 得 或 . 当 时，方程为 ， 表示圆心为 且半径为 的圆的右半圆； 当 时，方程为 ， 表示圆心为 且半径为 的圆的左半圆. 综上所述，得方程 表示的曲线为两个半圆. 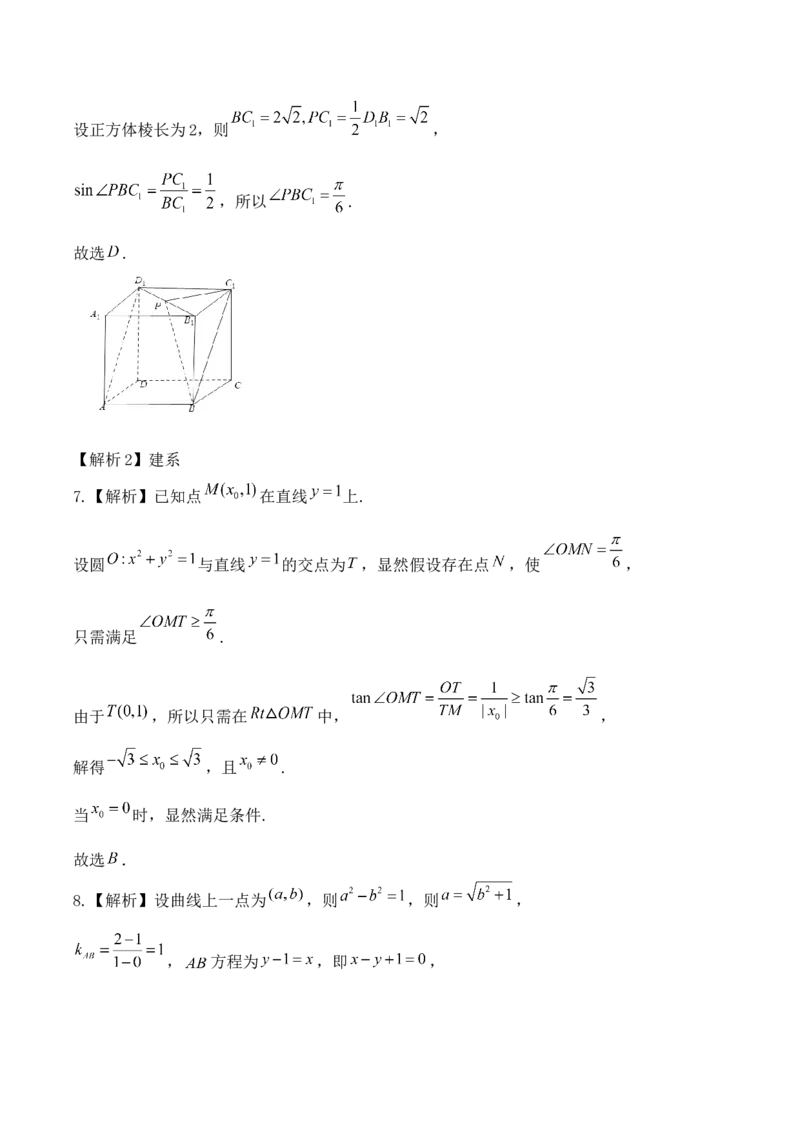故选 ． 6.【解析1】如图，连接 ，因为 ∥ ，所以 或其补角为直线 与 所成的角. A B C D 因为 平面 1 1 1 1，所以 ， 又 ， ， 所以 平面 ，所以 .设正方体棱长为2，则 ， ，所以 . 故选 . 【解析2】建系 7.【解析】已知点 在直线 上. 设圆 与直线 的交点为 ，显然假设存在点 ，使 ， 只需满足 . 由于 ，所以只需在 中， ， 解得 ，且 . 当 时，显然满足条件. 故选 ． 8.【解析】设曲线上一点为 ，则 ，则 ， ， 方程为 ，即 ，根据点到直线的距离公式， 到 的距离为 ， 设 ， 由于 ，显然 关于 单调递减， ，无最小值， 即 中， 边上的高有最大值，无最小值， 又 一定，故面积有最大值，无最小值. 故选 . 9.【解析】∵实数 满足方程 ，表示以 为圆心，半径等于 的圆． 过原点作圆的切线 ，由 ，求得 ，可得 的最大值为 ， 的最小值 为 ，故 正确． 令 ，直线与圆相切时，根据圆心到直线的距离 ，求得 ,则 的最大值为 ，故 错误． ∵ 表示圆上的点到原点的距离，它的最小值为圆心到原点的距离减去半径，故 的最小值为 ，故 错误. 故选 ． 10.【解析】依题意， ， ，所以 ， 选项，圆锥的体积为 ， 选项正确； 选项，圆锥的侧面积为 选项错误；选项，设 是 的中点，连接 ，则 ，所以 是二面角 的平面角，则 ，所以 ，故 ，则 ， 选项正确； 选项， ，所以 ， 选项错误. 故选 . 11.【解析】 选项：直线 过点 ，所以抛物线 的焦点 ， 所以 ，则 选项正确，且抛物线 的方程为 . 选项：设 ， 由 消去 并化简得 ， 解得 ，所以 ， 选项正确. 也可以由焦点弦长公式 . 选项：直线 ，即 ， 到直线 的距离为 ， 所以三角形 的面积为 ， 由上述分析可知 ，所以 ， 所以三角形 不是等腰三角形， 选项错误. 选项：设 的中点为 ， 到直线 的距离分别为 ， 因为 ， 即 到直线 的距离等于 的一半，所以以 为直径的圆与直线 相切， 选项正确. 故选 . 12.【解析】设递增等比数列 前n项和为 ,公比为 . 由 ，可得 ， 解得 ，或 (舍去)， 则 ， , 则数列 的前10项和为 . 故答案为 ． 13.【解析】由 ， 及余弦定理得 . 设 外接圆半径为 ，则由正弦定理得 . 设直棱柱的外接球半径为 ，则 ， . 故答案为 .14. 【 解 析 】 椭 圆 的 右 焦 点 为 ， 设 为 椭 圆 上 一 点 ， 易 得 ， 当 时， . 1 1 [ ,0) (0, ]  时， ，故d 的取值范围为 10 10 . 同理，当 15.【解析】(1)设 的方程为 ， ………1分 由 ，得 . ………2分 设 ，则 ， ………4分 , ………5分 ， ………6分 . ………7分 (2)由(1)得 ， ………9分 ∴ ， ………11分 ∴ ， ………12分∴ . ………13分 16.【解析】(1)证明：由已知有 ， ① ………1分 ， ② ………2分 ② ①可得 ， ………4分 整理得 ， ………6分 由等差数列定义得 为等差数列. ………7分 (2)由(1)可得 ， ， . 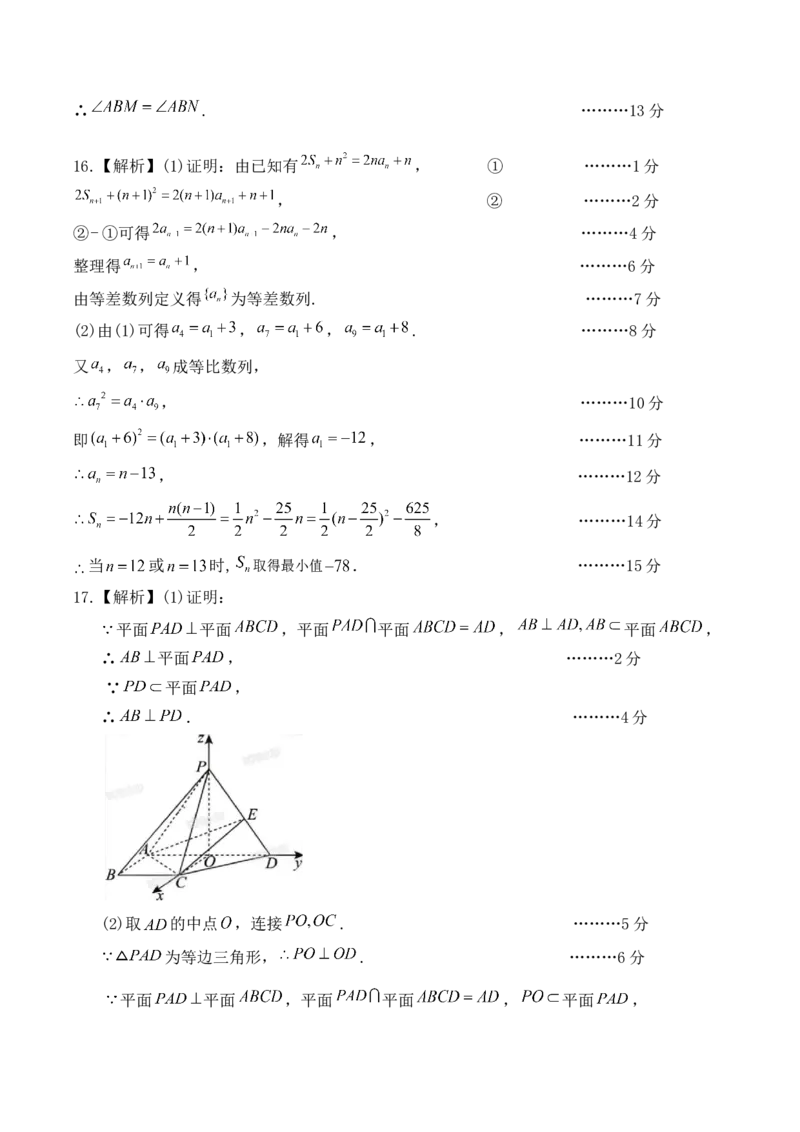………8分 又 ， ， 成等比数列， ， ………10分 即 ，解得 ， ………11分 ， ………12分 ， ………14分 当 或 时, 取得最小值 ． ………15分 17.【解析】(1)证明： 平面 平面 ，平面 平面 ， 平面 ， ∴ 平面 ， ………2分 ∵ 平面 ， ∴ ． ………4分 (2)取 的中点 ，连接 . ………5分 为等边三角形， . ………6分 平面 平面 ，平面 平面 ， 平面 ，平面 . ………7分 ， 四边形 是平行四边形， . ………8分 ， 两两垂直. ………9分 以 为坐标原点，直线 分别为 轴， 轴， 轴建立空间直角坐标系， 则 ， ， .…10分 令 ， ， . ………11分 设平面 的法向量为 ， 则 , 取 ，得 . ………12分 易知平面 的一个法向量为 ， ………13分 ， 化简得 , 解得 或 . ………14分又 ， ，即 ， 线段 上存在点 ，使得平面 与平面 夹角的余弦值为 , 此时 . ………15分 c 1200 18.【解析】(1)由题意，得 1 ，并且 c 1.08c 100 n1 n ． ① ………2分 c k  r(c k) (2)将 n1 n 化成 c  rc rk k． ② ………4分 n1 n r 1.08, 比较①②的系数，可得 ………6分 k rk  100. r 1.08, 解这个方程组，得 ………8分 k 1250. 所以(1)中的递推公式可以化为c 12501.08(c 1250)． ………10分 n1 n (3)由(2)可知，数列 c 1250 是以50为首项，1.08为公比的等比数列，…12分 n 则(c 1 1250)(c 2 1250)(c 3 1250)  (c 10 1250) ………14分 . ………16分 S c c c  c 125010724.311775.7 11776 所以 10 1 2 3  10 . ………17分 19．【解析】(1)由题可得 , ………1分 ，即椭圆 的长半轴长为 ，短半轴长为 ， ………2分. ………3分 (2)当 时，椭圆 . ………4分 又圆 ， ………5分 则圆心 ，半径 ，如图. 点 在椭圆上， ， ① ………6分 又直线 分别与圆 相切于 两点， ，且 . 四边形 为菱形， 所以四边形 为正方形， ………7分 ， , ② ………8分 由①②得 或 ， ………9分 圆 的方程为 或 . ………10分 (3) 直线 分别与圆 相切，且直线 的斜率乘积为定值， 直线 斜率都存在.设直线 的方程为 ，直线 的方程为 . ………11分 到直线 的距离都为2， ， ………12分 即 , ， 为方程 的两根， . ………13分 又点 在椭圆 上， ， . ………14分 直线 的斜率乘积为定值，设定值为 ， 则 对 恒成立， ………15分 即 对 恒成立， ,解得 , ………16分 的值为2．声明 ………17分：试题解析著作 权属所有，未经书面同意，不得复制发布日期：2025/12/22 20:00:34；用户：王伟琪； 邮箱：mkz18@xyh.com；学号：45336144