文档内容
高 2024 届高三第一学期期中考试
数学试题
(数学试题卷共6页,考试时间120分钟,满分150分)
注意事项:
1.答卷前,考生务必将自己的学校、姓名、考号填写在答题卡上.
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改
动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上.写在
本试卷上无效.
3.考试结束后,将本试卷和答题卡一并收回.
一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一
项是符合题目要求的.
1. 设 均为非空集合,且满足 ,则 ( )
A. B. C. D.
2. 已知命题 ,命题q:复数 为纯虚数,则命题 是 的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
3. 已知向量 , 的夹角为 ,且 ,则向量 在向量 上的投影向量为( )
A. B. C. D.
4. 《几何原本》卷 的几何代数法(以几何方法研究代数问题)成了后世西方数学家处理问题的重要依据.
通过这一原理,很多的代数的公理或定理都能够通过图形实现证明,也称之为无字证明.现有如图所示图
形,点 在半圆 上,点 在直径 上,且 ,设 , ,则该图形可以完成的
无字证明为( )
第 1 页 共 6 页A. B.
C. D.
5. 已知数列 均为等差数列,且 ,设数列 前 项的和为 ,
则 ( )
.
A 84 B. 540 C. 780 D. 920
6. 函数 的最大值为( )
A. 2 B. C. 0 D.
7. 为落实立德树人的根本任务,践行五育并举,某学校开设 三门劳动教育校本课程,现有甲、乙、
丙、丁、戊五位同学报名参加该校劳动教育校本课程的学习,每位同学仅报一门,每门至少有一位同学参
加,则不同的报名方法有( )
.
A 60种 B. 150种 C. 180种 D. 300种
8. 已知函数 ,若方程 有两个不相等的实数根,则实数 的取值范围是(
)
A. B. C. D.
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符
合题目要求,全部选对的得5分,部分选对的得2分,有选错的得0分.
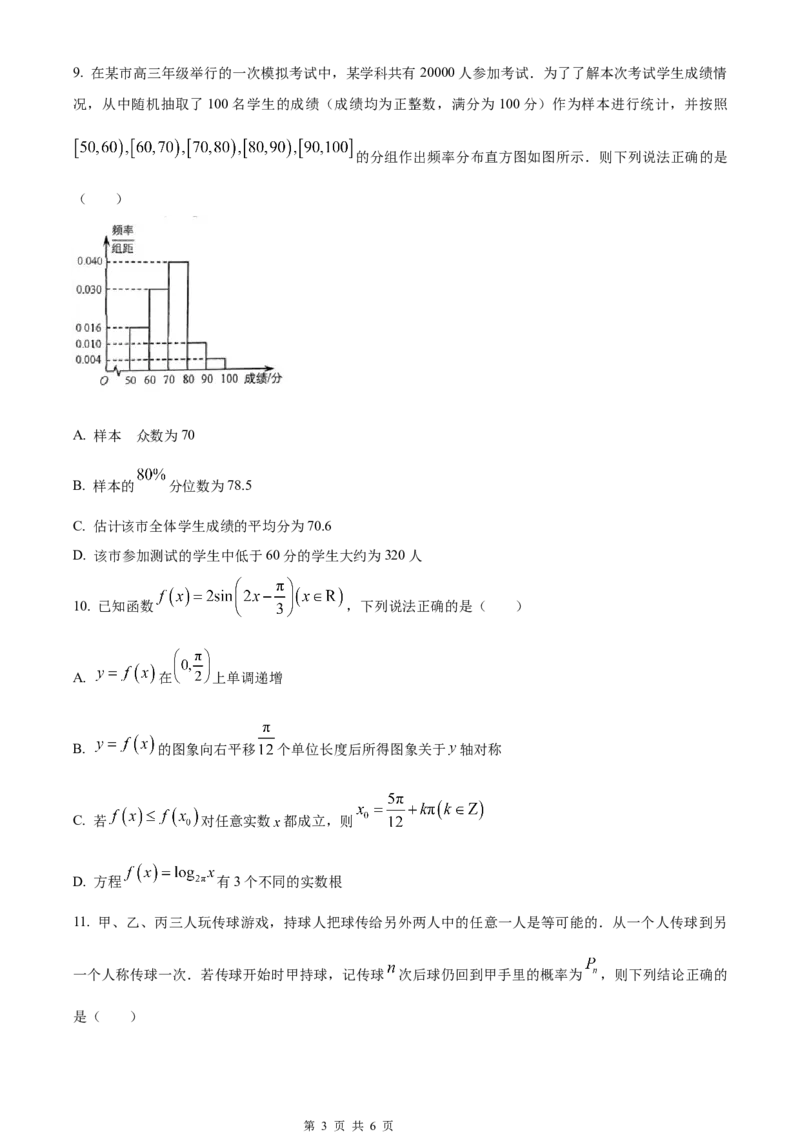
第 2 页 共 6 页9. 在某市高三年级举行的一次模拟考试中,某学科共有20000人参加考试.为了了解本次考试学生成绩情
况,从中随机抽取了100名学生的成绩(成绩均为正整数,满分为100分)作为样本进行统计,并按照
的分组作出频率分布直方图如图所示.则下列说法正确的是
( )
的
A. 样本 众数为70
B. 样本的 分位数为78.5
C. 估计该市全体学生成绩的平均分为70.6
D. 该市参加测试的学生中低于60分的学生大约为320人
10. 已知函数 ,下列说法正确的是( )
A. 在 上单调递增
B. 的图象向右平移 个单位长度后所得图象关于 轴对称
C. 若 对任意实数 都成立,则
D. 方程 有3个不同的实数根
11. 甲、乙、丙三人玩传球游戏,持球人把球传给另外两人中的任意一人是等可能的.从一个人传球到另
一个人称传球一次.若传球开始时甲持球,记传球 次后球仍回到甲手里的概率为 ,则下列结论正确的
是( )
第 3 页 共 6 页A. B. C. D.
12. 已知 ,则下列结论正确的是( )
A. B. C. D.
三、填空题:本大题共4小题,每小题5分,共20分.
13. 的展开式中, 的系数为__________(用数字作答).
14. 曲线 在 处的切线的倾斜角为 ,则 ______.
15. 定义:在数列 中, ,其中 为常数,则称数列 为“等比差”数列,已
知“等比差”数列 中, , ,则 ______.
16. 若 是定义在 上的函数,且 为奇函数, 为偶函数.则 在区间
上的最小值为______.
四、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.
17. 在 中,内角 的对边分别为 .
(1)求 ;
(2)若 ,点 在边 上,且 ,求 面积的最大值.
18. 2023年9月23日第19届亚运会在中国杭州举行,其中电子竞技第一次列为正式比赛项目.某中学对
该校男女学生 否是喜欢电子竞技进行了调查,随机调查了男女生人数各200人,得到如下数据:
男生 女生 合计
喜欢 120 100 220
第 4 页 共 6 页不喜欢 80 100 180
合计 200 200 400
的
(1)根据表中数据,采用小概率值 独立性检验,能否认为该校学生对电子竞技的喜欢情况与
性别有关?
(2)为弄清学生不喜欢电子竞技的原因,采用分层抽样的方法从调查的不喜欢电子竞技的学生中随机抽
取9人,再从这9人中抽取3人进行面对面交流,求“至少抽到一名男生”的概率;
(3)将频率视为概率,用样本估计总体,从该校全体学生中随机抽取10人,记其中对电子竞技喜欢的人
数为 ,求 的数学期望.
参考公式及数据: ,其中 .
0.15 0.10 0.05 0.025 0.01
2.072 2.706 3.841 5.024 6.635
19. 已知数列 的前 项和为 ,且 .
(1)求 的通项公式;
(2)设 ,若对任意 都有 成立,求实数 的取值范围.
20. 当前,新一轮科技革命和产业变革蓬勃兴起,以区块链为代表的新一代信息技术迅猛发展,现收集某
地近6年区块链企业总数量相关数据,如下表:
201 202
年份 2017 2019 2021 2022
8 0
编号 1 2 3 4 5 6
企业总数量 (单位:百
50 78 124 121 137 352
个)
(1)若用模型 拟合 与 的关系,根据提供的数据,求出 与 的经验回归方程;
(2)为了促进公司间的合作与发展,区块链联合总部决定进行一次信息化技术比赛,邀请甲、乙、丙三
第 5 页 共 6 页家区块链公司参赛.比赛规则如下:①每场比赛有两个公司参加,并决出胜负;②每场比赛获胜的公司与
未参加此场比赛的公司进行下一场的比赛;③在比赛中,若有一个公司首先获胜两场,则本次比赛结束,
该公司获得此次信息化比赛的“优胜公司”.已知在每场比赛中,甲胜乙的概率为 ,甲胜丙的概率为 ,
乙胜丙的概率为 ,若首场由甲乙比赛,求甲公司获得“优胜公司”的概率.
参考数据: ,其中,
参考公式:对于一组数据 ,其经验回归直线 的斜率和截距的最小二乘
估计分别为
21. 已知函数 .
(1)若 ,求 在 处的切线方程;
(2)若函数 在 上恰有一个极小值点,求实数 的取值范围;
(3)若对于任意 恒成立,求实数 的取值范围.
22. 已知函数 .
(1)若函数 是减函数,求 的取值范围;
(2)若 有两个零点 ,且 ,证明: .
第 6 页 共 6 页