2006年天津高考文科数学真题及答案_数学高考真题试卷_旧1990-2007·高考数学真题_1990-2007·高考数学真题·PDF_天津

2006 年天津高考文科数学真题及答案 本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共150分，考试用时120分 钟．第Ⅰ卷1至2页，第Ⅱ卷3至10页．考试结束后，将本试卷和答题卡一并交回． 祝各位考生考试顺利！ 第Ⅰ卷 注意事项： 1．答第Ⅰ卷前，考生务必将自己的姓名、准考证号、科目涂写在答题卡上，并在规定 位置粘贴考试用条形码． 2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑．如需改动，用橡 皮擦干净后，再选涂其他答案标号．答在试卷上的无效． 3．本卷共10小题，每小题5分，共50分． 参考公式： 如果事件A，B互斥，那么P(AB) P(A)P(B) 如果事件A，B相互独立，那么P(A· B) P(A·) P(B) 如果事件A在一次试验中发生的概率是P，那么n次独立重复试验中恰好发生k次的 概率P (k)CkPk(1P)nk n n 一、选择题：在每小题列出的四个选项中，只有一项是符合题目要求的． 1．已知集合Ax|3≤x≤1，B  x ≤2  ，则A B（ ）  Ａ．x|2≤x≤1 Ｂ．x|0≤x≤1 Ｃ．x|3≤x≤2 Ｄ．x|1≤x≤2 2．设a 是等差数列，a a a 9，a 9，则这个数列的前6项和等于（ ） n 1 3 5 6 Ａ．12 Ｂ．24 Ｃ．36 Ｄ．48 y≤x  3．设变量x，y满足约束条件x y≥2 ，则目标函数Z 2x y的最小值为（ ）  y≥3x6  Ａ．2 Ｂ．3 Ｃ．4 Ｄ．9 4．设Plog 3，Qlog 2，Rlog (log 2)，则（ ） 2 3 2 3 Ａ．RQ P Ｂ．P RQ Ｃ．Q R P Ｄ．R PQ  π π 5．设，   ， ，那么“”是“tantan”的（ ）  2 2 第1页 | 共12页Ａ．充分而不必要条件 Ｂ．必要而不充分条件 Ｃ．充分必要条件 Ｄ．既不充分也不必要条件 6．函数y  x2 11(x0)的反函数是（ ） Ａ．y  x2 2x(x0) Ｂ．y  x2 2x(x0) Ｃ．y  x2 2x(x2) Ｄ．y  x2 2x(x2) 7．若l为一条直线，，，为三个互不重合的平面，给出下面三个命题： ①，；②，∥；③l∥，l ． 其中正确的命题有（ ） Ａ．0个 Ｂ．1个 Ｃ．2个 Ｄ．3个 8．椭圆的中心为点E(1，0)，它的一个焦点为F(3，0)，相应于焦点F 的准线方程为 7 x ，则这个椭圆的方程是（ ） 2 2(x1)2 2y2 2(x1)2 2y2 Ａ．  1 Ｂ．  1 21 3 21 3 (x1)2 (x1)2 Ｃ．  y2 1 Ｄ．  y2 1 5 5 9．已知函数 f(x)asinxbcosx（a，b为常数，a0，xR）的图象关于直线 π 3π x 对称，则函数y  f( x)是（ ） 4 4 Ａ．偶函数且它的图象关于点(π，0)对称 3π  B．偶函数且它的图象关于点 ，0 对称  2  3π  Ｃ．奇函数且它的图象关于点 ，0 对称  2  Ｄ．奇函数且它的图象关于点(π，0)对称 10．如果函数 f(x)ax(ax 3a2 1)(a 0且a 1)在区间0，∞上是增函数，那么实数 a的取值范围是（ ）  2  3   3  Ａ． 0，  Ｂ． ，1  Ｃ． 1，3  Ｄ．  ，∞   3  3  2  第2页 | 共12页第Ⅱ卷 注意事项： 1．答卷前将密封线内的项目填写清楚． 2．用钢笔或圆珠笔直接答在试卷上． 3．本卷共12小题，共100分． 三 题号 二 总分 17 18 19 20 21 22 得分 得分 评卷人 二、填空题：本大题共6小题，每小题4分，共24分．把答案填在题中 横线上． 7  1  11． x 的二项展开式中x的系数是 （用数字作答）．    x       12．设向量a与b的夹角为，a(3，3)，2ba(1，1)，则cos ． 13．如图，在正三棱柱 ABCABC 中， AB1．若二面角 1 1 1 A C 1 1 B CABC 的大小为60，则点C 到直线AB的距离为 ． 1 1 1 A C 3 14．若半径为 1 的圆分别与 y轴的正半轴和射线 y  x(x≥0)相 3 B 切，则这个圆的方程为 ． 15．某公司一年购买某种货物400吨，每次都购买x吨，运费为4万元／次，一年的总存储 费用为4x万元，要使一年的总运费与总存储费用之和最小，则x 吨． 16．用数字0，1，2，3，4组成没有重复数字的五位数，则其中数字1，2相邻的偶数有 个（用数字作答）． 三、解答题：本大题共6小题，共76分．解答应写出文字说明，证明过程或演算步骤． 得分 评卷人 17．（本小题满分12分） 5 π π π 已知tancot ，  ， ．求cos2和sin(2 )的值． 2 4 2 4 得分 评卷人 18．（本小题满分12分） 第3页 | 共12页甲、乙两台机床相互没有影响地生产某种产品，甲机床产品的正品率是0.9，乙机床产品的 正品率是0.95． （Ⅰ）从甲机床生产的产品中任取3件，求其中恰有2件正品的概率（用数字作答）； （Ⅱ）从甲、乙两台机床生产的产品中各任取1件，求其中至少有1件正品的概率（用数字 作答）． 得分 评卷人 19．（本小题满分12分） 如图，在五面体ABCDEF 中，点O是矩形ABCD的对角线的交点，面CDE是等边三角 1 形，棱EF ∥ BC． 2 F E （Ⅰ）证明FO∥平面CDE； （Ⅱ）设BC  3CD，证明EO平面CDF ． A D O B C 得分 评卷人 20．（本小题满分12分） 1 π 已知函数 f(x)4x33x2cos ，其中xR，为参数，且0≤≤ ． 32 2 （Ⅰ）当cos0时，判断函数 f(x)是否有极值； （Ⅱ）要使函数 f(x)的极小值大于零，求参数的取值范围； （Ⅲ）若对（Ⅱ）中所求的取值范围内的任意参数，函数 f(x)在区间(2a1，a)内都是 增函数，求实数a的取值范围． 得分 评卷人 21．（本小题满分14分） x x 已知数列x 满足x  x 1，并且 n1  n （为非零参数，n2，3，4，… ）． n 1 2 x x n n1 （Ⅰ）若x，x，x 成等比数列，求参数的值； 1 3 5 （ Ⅱ ） 设 01， 常 数 kN且 k≥3． 证 明 第4页 | 共12页x x x k 1k  2k …  nk  (nN)． x x x 1k 1 2 n 得分 评卷人 22．（本小题满分14分） 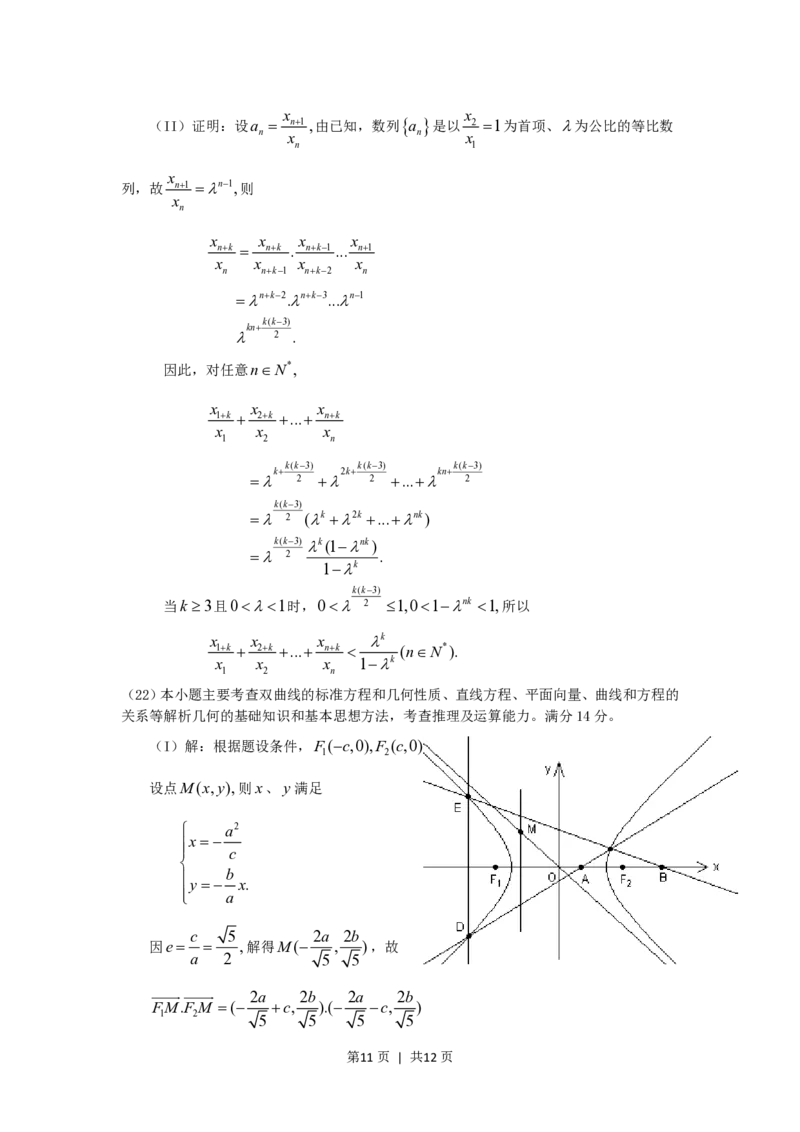y 如图， Ｅ 双曲线 l x2 y2 C  1(a0，b0)的 M B a2 b2 F 1 O A F 2 x 5 离心率为 ． F，F 分别为 2 1 2 D 左、右焦点，M 为左准线与渐   1 近线在第二象限内的交点，且FM· F M  ． 1 2 4 （Ⅰ）求双曲线的方程；  1  （Ⅱ）设A(m，0)和B  ，0  (0m1)是x轴上的两点，过点A作斜率不为0的直线l， m  使得l交双曲线于C，D两点，作直线BC交双曲线于另一点E．证明直线DE垂 2006年天津高考文科数学真题参考答案 一．选择题：本题考查基本知识和基本运算。每小题5分，满分50分。 （1）A （2）B （3）B （4）A （5）C （6）D （7）C （8）D （9）D （10）B 二．填空题：本题考查基本知识和基本运算。每小题4分，满分24分。 3 10 （11）35 （12） （13） 3 10 （14）(x1)2 (y 3)2 1 （15）20 （16）24 一．选择题：本题考查基本知识和基本运算。每小题5分，满分50分。 题号 1 2 3 4 5 6 7 8 9 10 答案 A B B A C D C D D B （1 ）已知集合A{x|3 x1},B{x| x 2}={x|2≤x≤2}， 则A B＝x|2 x1，选A.  第5页 | 共12页（2 ）a 是等差数列，a a a 3a 9,a 3,a 9. ∴ d 2,a 1，则这个数 n 1 3 5 3 3 6 1 6(a a ) 列的前6项和等于 1 6 24，选B. 2 y x  （3）设变量x、 y满足约束条件x y2 ,在坐标系中画出可行域△ABC，A(2，0)，  y3x6  B(1，1)，C(3，3)，则目标函数z 2x y的最小值为3，选B. （4）Plog 31,0Qlog 21,Rlog (log 2)0, 则RQ P，选A. 2 3 2 3     （5）在开区间( , )中，函数 y tanx为单调增函数，所以设,( , ),那么 2 2 2 2 ""是"tantan"的充分必要条件，选C. （6）由函数 y  x2 11(x0)解得x (y1)2 1 y2 2y(y>2)，所以原函 数的反函数是y  x2 2x(x2)，选D. （7）若l为一条直线，、、为三个互不重合的平面，下面三个命题： ① ,;不 正 确 ； ② ,∥;正 确 ； ③ l//,l .正确，所以正确的命题有2个，选C. （8）椭圆的中心为点E(1,0),它的一个焦点为F(3,0),∴ 半焦距c2，相应于焦点F 7 a2 5 的 准 线 方 程 为 x . ∴  ， a2 5,b2 1， 则 这 个 椭 圆 的 方 程 是 2 c 2 (x1)2  y2 1，选D. 5 （ 9 ） 已 知 函 数 f(x)asinxbcosx (a、 b为 常 数 ,a0,xR)， ∴  f(x) a2 b2 sin(x)的周期为 2π，若函数的图象关于直线 x 对称，不妨设 4  3 3  f(x)sin(x )，则函数 y  f( x)=sin( x )sin(x)sinx，所以 4 4 4 4 3 y  f( x)是奇函数且它的图象关于点(,0)对称，选D. 4 （10）函数yax(ax 3a2 1)(a0且a1)可以看作是关于ax的二次函数，若a>1，则 第6页 | 共12页3a2 1 y ax是增函数，原函数在区间[0,)上是增函数，则要求对称轴 ≤0，矛盾；若 2 0