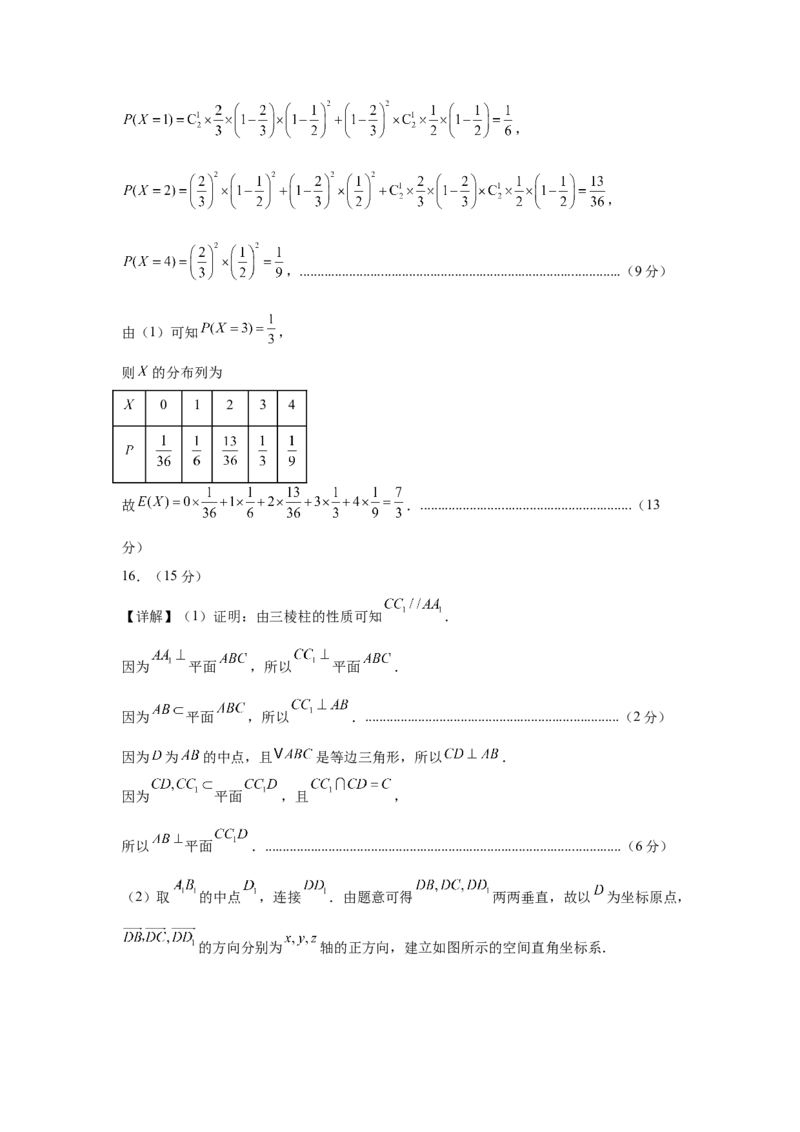文档内容
2025 年 1 月“八省联考”考前猜想卷 02
数学·参考答案与评分标准
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一
项是符合题目要求的。
1 2 3 4 5 6 7 8
C B A A A D B A
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合
题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9 10 11
ABD AC ABD
三、填空题:本题共3小题,每小题5分,共15分。
12.240或3840 13. 14.
四、解答题:本题共5小题,共77分。解答应写出文字说明、证明过程或演算步棸。
15.(13分)
【详解】(1)学生甲恰好答对3道题有以下两种情况:
第一种情况是学生甲答对 组的2道题和 组的1道题,
其概率 ;...........................................................................(2分)
第二种情况是学生甲答对 组的l道题和 组的2道题,
其概率 .
故学生甲恰好答对3道题的概率 ..............................................(5分)
(2)由题意可知 的所有可能取值为 .
,
学科网(北京)股份有限公司,
,
,...........................................................................................(9分)
由(1)可知 ,
则 的分布列为
0 1 2 3 4
故 .............................................................(13
分)
16.(15分)
【详解】(1)证明:由三棱柱的性质可知 .
因为 平面 ,所以 平面 .
因为 平面 ,所以 .........................................................................(2分)
因为 为 的中点,且 是等边三角形,所以 .
因为 平面 ,且 ,
所以 平面 ......................................................................................................(6分)
(2)取 的中点 ,连接 .由题意可得 两两垂直,故以 为坐标原点,
的方向分别为 轴的正方向,建立如图所示的空间直角坐标系.设 ,则 ,
故 ....................................(8
分)
设平面 的法向量为 ,
则 令 ,得 .
设平面 的法向量为 ,
则 令 ,得 .
设平面 与平面 所成的锐二面角为 ,
则 ,
即平面 与平面 所成锐二面角的余弦值为 .............................................(15
分)
17.(15分)
【详解】(1) , ,
学科网(北京)股份有限公司, ,
所以在点(1,f (1))处的切线方程为 ,
整理得: ;..........................................................................................(4分)
(2)函数 定义域为(0,+∞), ..........................(6分)
当 时,f'(x)≥0,此时 在(0,+∞)上单调递增;
当 时,令 ,得 ,
此时在 上f'(x)<0, 在 单调递减,
在 上f'(x)>0, 在 单调递增,
综上:
时, 的递增区间为(0,+∞),无递减区间;
时, 的递减区间为 ,递增区间为 ;..........................................(9分)
(3)由(2)可知,当 时, 才有两个不相等的实根,且 ,
则要证 ,即证 ,即证 ,
而 ,则 ,否则方程不成立),
所以即证 ,化简得 ,................................................................(11
分)
令 ,则 ,
当 时, ,所以 在(0,1)单调递减,
当 时, ,所以 在(1,+∞)单调递增,...........................................(13分)所以 ,而 ,所以 ,
所以 ,得证....................................................................................................(15分)
18.(17分)
【详解】(1)设动圆的半径为r,圆 的圆心 ,半径 ,
显然点 在圆 内,则 ,
于是 ,
因此动点M的轨迹C是以 , 为焦点,长轴长为4的椭圆,.................................(2分)
长半轴长 ,半焦距 ,则短半轴长 ,
所以轨迹C的方程为 .........................................................................................(4
分)
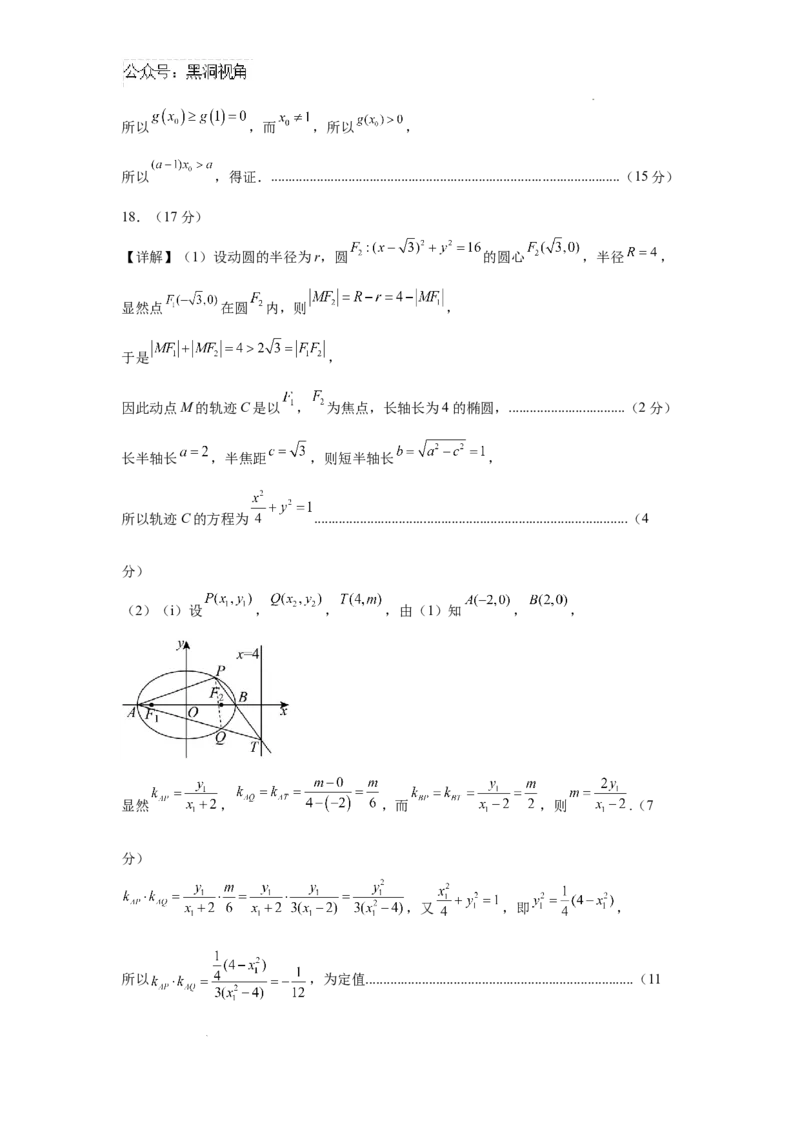
(2)(i)设 , , ,由(1)知 , ,
显然 , ,而 ,则 .(7
分)
,又 ,即 ,
所以 ,为定值............................................................................(11
学科网(北京)股份有限公司分)
(ii)由 消去x得 ,
,
由(i)得 ,又 ,......................................(14
分)
则
,解得 ,满足 ,
因此直线PQ的方程为 ,
所以直线PQ过定点 .................................................................................................(17分)
19.(17分)
【详解】(1)由 ,且 为“2数列”,得 ,即 ,...........(2
分)
则 ,
,
,
..............................................................(5分)
(2)设数列{b }的公比为 ,
n
由 ,得 ,....................................................................................(6分)即 ,
则 .
两式相减得 ,
即 .
因为 是首项为2的“ 数列”,所以 ,....................................................(8
分)
即 ,
所以 ,
即 对任意的 恒成立.
因为 , ,
则 ,即 ,
解得 , ..........................................................................................................(11
分)
又由 ,即 ,得 ,所以 .
检验可知 符合要求,故数列{b }的通项公式为 ...................................(12
n
分)
(3)因为 为“ 数列”,所以 ,
即 对任意的 恒成立,
因为 , ,所以 .
再结合 , , ,反复利用 ,
可得对任意的 , .
设函数 ,则 ......................................................................(15
分)
由 ,得 .
当 时,f'(x)<0,所以 在(1,+∞)上单调递减.
学科网(北京)股份有限公司所以当 时, ,即 .
又 ,所以 .
可得 , , , ,
累加可得 ,
即 ,即 ,
所以 ..............................................................................................................(17
分)