数学试题参考答案_2024-2025高三（6-6月题库）_2024年11月试卷_1126江西省萍乡实验学校2025届高三月考试卷(四)暨长郡十八校联考考前演练

萍乡实验学校2025届高三月考试卷（四）
大联考
暨长郡十八校联考考前演练
数学参考答案
一、选择题：本题共8小题，每小题5分，共40分。
题号 1 2 3 4 5 6 7 8
答案 C C D B B D C B
4．B【解析】由图可知，两个函数图象都在x轴上方，所以�′ � >0， f x 单调递增，所以实线为 f x 的
图象，虚线为�′ � 的图象， f 0 f01，对A，y f(x)10，y f(x)x单调递增，无最大值，A
exf(x) f(x) e0f(0) f(0)
错误；对B，y ，y|  0，由图可知，当x0时， f x fx0，当
f(x)2 x0 f(0)2
x0时， f x fx0，所以y
ex
在 ,0 上单调递减，在 0,+∞ 上单调递增，所以当x0时，函
f(x)
e0
数取得最小值y  1，B正确；对C，y f(x) f(x)  ex，由图可知 f x fx0，所以
min f(0)
fx f(x)
y f(x)ex在�上单调递增，无最大值，C错误；对D，y ，由图可知，当x0时，
ex
f(x)
f x fx0，当x0时， f x fx0，所以函数y 在 ,0 上单调递增，在 0,+∞ 上单调
ex
f(0)
递减，当x0时，函数取得最大值y  1，D错误.
max e0
1  1 
5．B【解析】因为4x2  y，即x2  y，因此F0, ，易知直线l是C的准线，则
4  16
PF  AP ，如图，又 PB  PB ，FPBAPB，所以△FPB≌△APB，得
2
BF 1
PFBPAB90，四边形ABFP为正方形，故△BFP的面积为  .
2 128
6．D【解析】因为对任意的x,x 0, ，且x x ，都有 x 2 fx 1 x 1 f x 2  0，即对任意两个不相等的正实数
1 2 1 2 x x
1 2
x 2 fx 1 x 1 fx 2  fx 1   fx 2  f x  fx 
x ,x ，不妨设0 x  x ，都有 xx x x ，所以有 1  2 ，所以函数
1 2 1 2 1 2  1 2 0 x x
x x x x 1 2
1 2 1 2
gx f x 是 0,+∞ 上的减函数，由 f x 的定义域为 0,+∞ ，则在 f x2 f  x24  中满足
x x2
  x20 ，解得x2，当�>2时， f x2 f  x24   f x2  f  x24  ，则gx2 g  x24  ，
x240
x2 x2 x24
所以0 x2 x24，解得x2，故不等式 f x2 f  x24  的解集为 2, ．
x2
7．C【解析】解法一（正难则反）：存在1i j4，i, jN*，使得 a a 1表示所取的4个数中总有相邻
i j
的数，直接求解较复杂，考虑正难则反的方法．假设a a a a ，若不存在1i j4，使得 a a 1，
1 2 3 4 i j
则1a a 1a 2a 37，所以符合条件的取法种数为C4 C4 175．
1 2 3 4 10 7
解法二（转化法）：若存在1i j4，i, jN*，使得 a a 1，则所取的4个数中至少有2个是连续正整数
i j
，若只有2个是连续正整数，问题转化为把6个相同的白球与4个相同的红球排成一行，要求只有2个红球相邻，
先把6个白球排成一行，再用插空法排红球，排法种数为C3C1C2 105．同理可得若只有3个是连续正整数，排
7 3 2
法种数为C2A2 42．若4个都是连续正整数，排法种数为7．若4个数中有2个是连续正整数，另外2个也是连续
7 2
正整数，但这4个数不是4个连续正整数，则排法种数为C2 21．所以符合条件的取法种数为10542721175.
7
数学参考答案（萍实版）-1
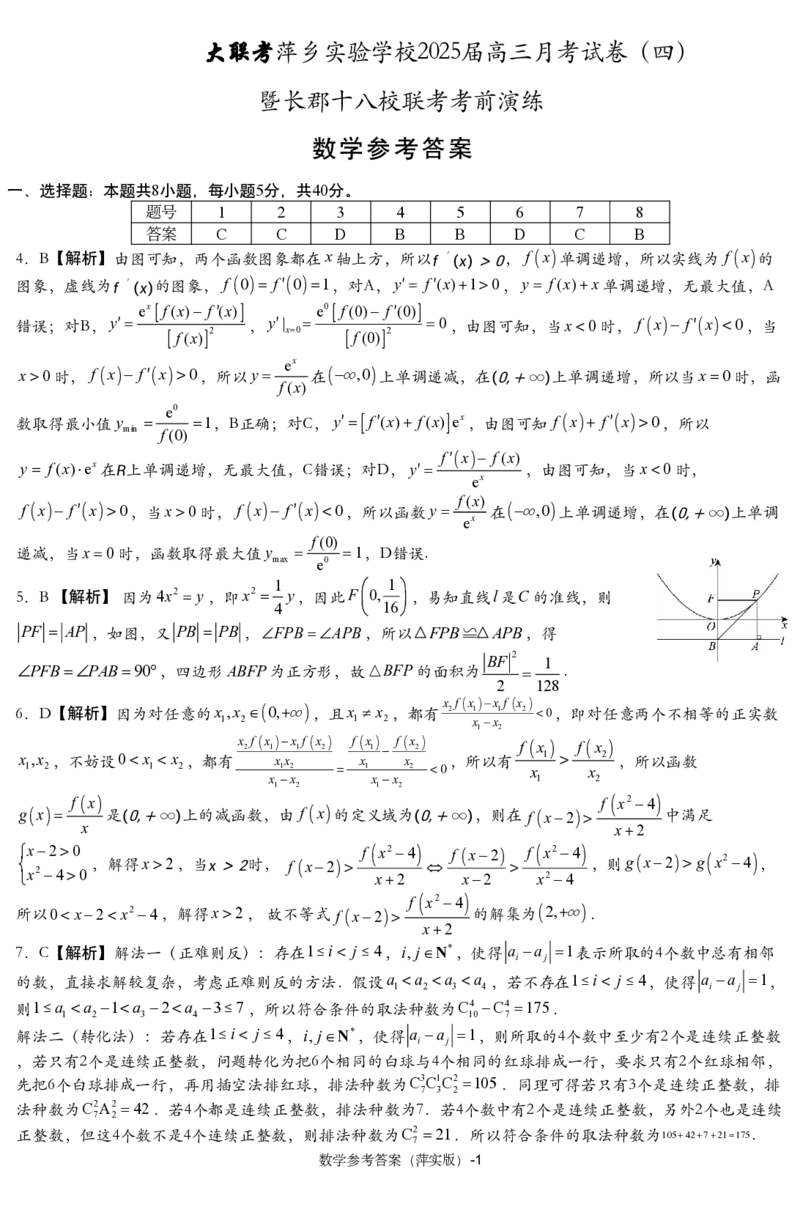
{#{QQABTYIEogiAAhAAAAhCAQFgCECQkhGCAYgGxEAMoAAASAFABCA=}#}8．B【解析】如图所示，取AB中点为F ，PFDEG，为方便计算，不妨设
2 3
PF CF 1，由PAPB AB AC BC ，可知PAPBABAC BC  ，又
3
2 2
D、E分别为所在棱靠近P端的三等分点，则FG PF  ，且ABPF，
3 3
ABCF、PF ∩CF F ，PF，CF 平面PCF，即AB平面PCF，又AB平面
ABC，则平面PCF 平面ABC，设肉馅球半径为r，CG x，由于H、I 、J分别
为所在棱中点，且沿平面HIJ 切开后，截面中均恰好不见肉馅，则P到CF的距离
d 1 2 4r  2  r
d 4r，sinPFC 4r ，S  1 4r  ，又S 1 x ，解得
PF △GFC 2 3 3 GFC  3  2
4
：x1，故cosPFC CF2FG2CG2 
1
9
1
 1 ，又cosPFC PF2CF2PC2  11PC2  1 ，解得PC  2 3 ，
2CFFG 21 2 3 2PFCF 211 3 3
3
2 2 2 2 4r 2 4 2
sinPFC ，所以：sinPFC  ，解得r  ，V  r3 ，由以上计算可知：PABC
3 3 1 6 球 3 81
2
为正三棱锥，故V  1 S d  1  1 ABAC sinBAC 4r  1  1  2 3  2 3  3 4 2  2 6 ，所以比值为 81   3 π.
粽 3 ABC 3 2 3 2 3 3 2 6 27 2 6 18
27
二、选择题：本题共3小题，每小题6分，共18分。
题号 9 10 11
答案 AD ABD ABC
 π  π
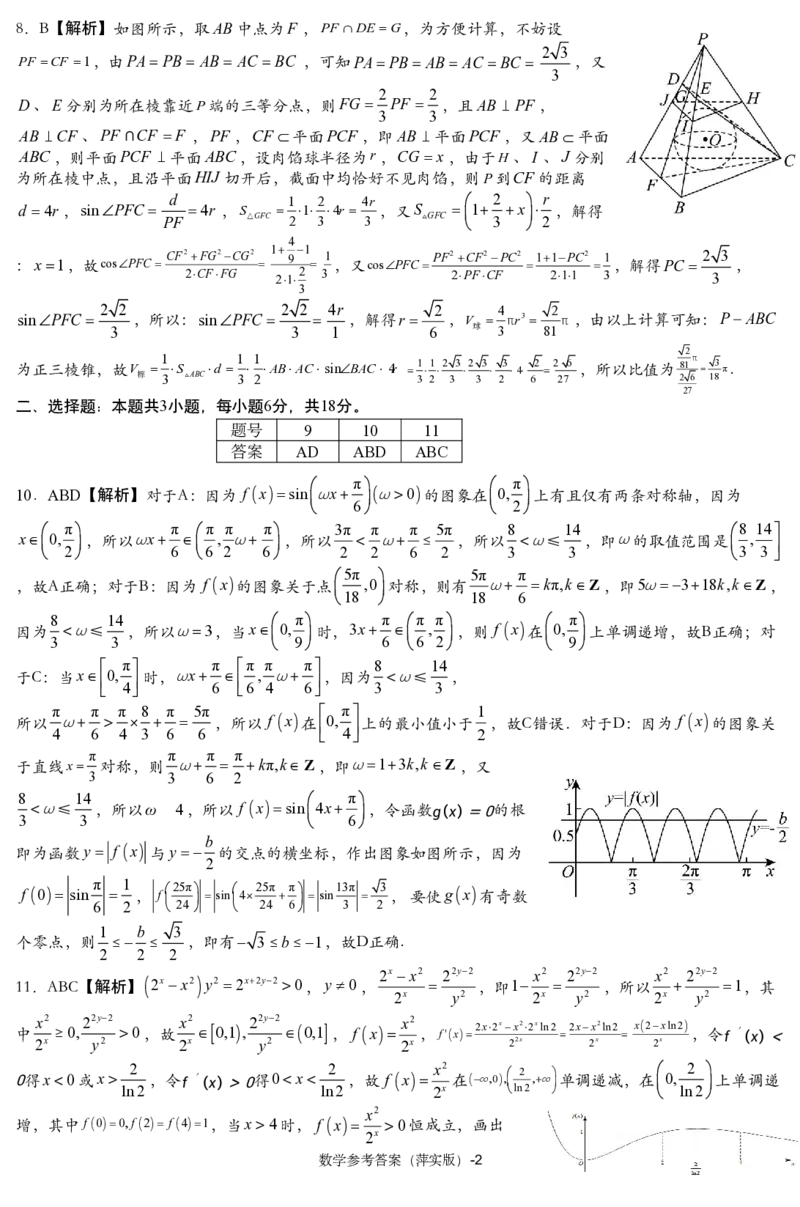
10 ABD【解析】对于A：因为 f xsinx  0的图象在0, 上有且仅有两条对称轴，因为
．  6  2
 π π π π π 3π π π 5π 8 14 8 14
x0, ，所以x  ,  ，所以    ，所以 ≤ ，即的取值范围是 ,

 2 6 6 2 6 2 2 6 2 3 3 3 3 
5π  5π π
，故A正确；对于B：因为 f x 的图象关于点 ,0对称，则有  kπ,kZ，即5318k,kZ，
18  18 6
因为 8 ≤ 14 ，所以3，当x  0, π 时，3x π    π , π ，则 f x 在  0, π 上单调递增，故B正确；对
3 3  9 6 6 2  9
 π π π π π 8 14
于C：当x  0,  时，x   ,  ，因为 ≤ ，
 4 6 6 4 6 3 3
π π π 8 π 5π  π 1
所以      ，所以 f x 在 0, 上的最小值小于 ，故C错误．对于D：因为 f x 的图象关
 
4 6 4 3 6 6  4 2
π π π π
于直线x 对称，则   kπ,kZ，即13k,kZ，又
3 3 6 2
8 14  π
≤ ，所以ω 4，所以 f xsin4x ，令函数� � =0的根
3 3  6
b
即为函数y f x 与y 的交点的横坐标，作出图象如图所示，因为
2
f 0 sin π  1 ， f   25π   sin  4 25π  π   sin 13π  3 ，要使gx 有奇数
6 2  24   24 6 3 2
1 b 3
个零点，则   ，即有 3b1，故D正确.
2 2 2
11．ABC【解析】  2x x2 y2 2x2y2 0，y0，
2x x2

22y2
，即1
x2

22y2
，所以
x2

22y2
1，其
2x y2 2x y2 2x y2
中 x2 0, 22y2 0，故 x2  0,1, 22y2 0,1  ， f x x2 ，fx 2x2xx22xln2  2xx2ln2  x2xln2 ，令�′� <
2x y2 2x y2 2x 22x 2x 2x
0得x0或x 2 ，令�′� >0得0 x 2 ，故 f x x2 在,0,   2 ,  单调递减，在  0, 2  上单调递
ln2 ln2 2x ln2   ln2
x2
增，其中f00,f2 f41，当x4时， f x 0恒成立，画出
2x
数学参考答案（萍实版）-2
{#{QQABTYIEogiAAhAAAAhCAQFgCECQkhGCAYgGxEAMoAAASAFABCA=}#}x2
fx 的图象，如下：
2x
故 f x
x2
 0,1的解集为  0,24, ，包含 4, ， 0,2，AB正确；令gy
22y2

4y1
，定义域为
2x y2 y2
4y1y2ln44y12y 4y1
,00, ，则gy  yln42，令gy0得
y4 y3
1 1 4y1  1 
y0或y ，令gy0得0 y ，故gy 在,0, ,单
ln2 ln2 y2 ln2 
 1 
调递增，在0,
上单调递减，且g1g21，gy0在 ,00,
恒
 ln2
成立，画出gy
4y1
的图象，如下：gy
4y1
0,1  的解集为 ,11,2 ，其中m0，故 1,2N
y2 y2
，C正确，D错误.
三、填空题：本题共3小题，每小题5分，共15分。
8
12 4 13 2 1 e 14 81
． ． 或 ．
四、解答题：本题共 5小题，共 77分。解答应写出文字说明、证明过程或演算步骤。
1
15 1 a2b sinA2sinB sinAcosB 2sinBcosB tanB
．（ ）由 及正弦定理可得 ，又 ， ， 2，
B0,π sinB 5 cosB 2 5 sin  B π sinBcos π cosBsin π  3 10 .
又 ， ， ，
5 5  4 4 4 10
2 b2 a2c22accosB
（ ）由余弦定理 ，
1 24 5a 12 5
a2 a236 a a4 5.
可得 ，解得 或
4 5 5
12 5 1 1 12 5 5 36
a ABC acsinB  6 
当 时， 的面积为 ；
5 2 2 5 5 5
1 1 5 36
a4 5 ABC acsinB 4 56 12. ABC 12.
当 时， 的面积为 2 2 5 综上可知， 的面积为 5 或
16 1 X 0,1,2,3
．（ ）解：由题知甲的总得分 的可能值为 ，
1,3,5,7 A4 24
不妨设甲四轮出的卡片上的数依次为 ，则乙四轮出的卡片共有 4 种情况，
1
X 0 2,4,6,8 PX 0
当 时，乙出的卡片上的数依次为 ，所以 24 ．
X 1 2,4,8,6 2,6,4,8 2,6,8,4 2,8,6,4 4,2,6,8
当 时，乙出的卡片上的数依次为 ； ； ； ； ；
11
4,6,2,8 4,6,8,2 4,8,6,2 6,4,2,8 6,4,8,2 8,4,6,2 PX 1
； ； ； ； ； ．所以 24．
X 2 2,8,4,6 4,2,8,6 4,8,2,6 6,2,4,8 6,2,8,4 6,8,2,4
当 时，乙出的卡片上的数依次为 ； ； ； ； ； ；
11
6,8,4,2 8,2,6,4 8,4,2,6 8,6,2,4 8,6,4,2 PX 2
； ； ； ； ．所以 24．
1
X 3 8,2,4,6 PX 3
当 时，乙出的卡片上的数依次为 ，所以 24．
X
因此甲的总得分 的分布列为
X 0 1 2 3
1 11 11 1
P
24 24 24 24
1 11 11 1 3
X EX0 1 2 3 
故甲的总得分 的数学期望为 24 24 24 24 2．
2 n Y PY 21PY 0PY 1
（ ）设 轮比赛后甲的总得分为 ，则 ．
n 1,3,5,7,···,2n1
不妨设甲 轮出的卡片上的数依次数 ，
n n!
则乙 轮出的卡片顺序有 种．
数学参考答案（萍实版）-3
{#{QQABTYIEogiAAhAAAAhCAQFgCECQkhGCAYgGxEAMoAAASAFABCA=}#}1
Y 0 2,4,6,8,···,2n PY 0
若 ，则乙出的卡片上的数依次为 ，所以 n!．
Y 1
若 ，即甲只有一张卡片上的数比乙的卡片上的数大，
n 1,3,5,7,···,2n1
不妨设甲 轮出的卡片上的数依次为 ，
n
乙 轮出的卡片上的数为：
 
B 2j1 jn,nN* b b b … b
中元素的一个排列： 1， 2， 3， ， n，
k  kN*,k n  b 2k1 b 2k1
故要满足题意，则存在唯一的 ，使得 k ，即 k ，
i  iN*,in  ik b 2i 2k1 2k 2
且对任意的 满足 ， i ．（提示：观察到 ， 均为 的倍数，接下来可以将研究
1,,2,3,···,n
对象转化到 的排列中进行研究，更容易理解）
b 2x k  kN*,k n  x k1 i  iN*,in  ik
令 n n，则问题转化为存在唯一的 ，使得 k ，且对任意的 满足 ，
x i b x x x … x
i ．（此处满足的条件是从上面的 k满足的条件转化而来，且 1， 2， 3， ， n的取值顺序不定）
k1 k2
易知 ，则 ．
ik1 x i 1ik1 x i x k
当 时， i ． 当 时， i ，且 k ，
1ik1 x i x x … x x a
设满足 ， i 的序列 1， 2， ， k1， k的个数为 k：
x k x x … x x 1,2,···,k2,k1
①当 k1 时， 1， 2， ， k2， k为 的一个排列，
1ik2 x i x x … x x a
故满足 ， i 的序列 1， 2， ， k2， k的个数为 k1；
x k1 x x … x x 1,2,···,k2,k
②当 k1 时， 1， 2， ， k2， k为 的一个排列，，
1ik2 x i x x … x x a
故满足 ， i 的序列 1， 2， ， k2， k的个数为 k1．
k k1 a 2a k3 a 2 a 2k1k2
（提示：注意 出现的位置与 等价） 综上， k k1 ，易得 2 ，故 k ，
x x … x x 1,2,···,k1,k 1ik1 x i x k
因为当且仅当序列 1， 2， ， k1， k为 时满足任意的 ， i ，且 k ，所以满
1ik1 x i x k x x … x x 2k11k2
足 ， i ，且 k 的序列 1， 2， ， k1， k的个数为 ．
k
k2,,n1,n
X 1
设第 轮甲卡片上的数比乙卡片上的数大， ，则根据以上推论可得满足 的情况有
n
 2k11    21222n1 n12nn1
（种）．
k2
2nn1 1 2nn1 2nn
PY 1 PY 21PY 0P Y 11  1
故 ．综上， ．
n! n! n! n!
2nn
Y 2 1
所以甲的总得分 不小于 的概率为 ．
n!
17 1 EABCD ABBC
．（ ）解法一：因为四棱锥 的底面为正方形，所以 ，
EAB60 AE2AB2
因为 ， ，
EAB BE2  AE2AB22AEABcosEAB2212221cos603
所以在 中，根据余弦定理得 ，
AE2 BE2AB2 ABBE
所以 ，所以 ，
BE∩BCB BE,BC BCE AB BCE
又 ， 平面 ，所以 平面 ．
        2    2   1
ABBE AB BAAE AB ABAE AB  AB  AE cos60 1 1 2  0
解法二：因为 2 ，
所以AB  BE ，所以 ABBE , 因为四棱锥 EABCD 的底面为正方形，所以 ABBC ，
BC∩BE B BE,BC BCE AB BCE
又 ， 平面 ，所以 平面 ．
2 EABCD D DA DC x y D
（ ）①在底面为正方形的四棱锥 中，以 为坐标原点， ， 分别为 ， 轴，过 且垂直于
ABCD z
平面 的直线为 轴建立如图所示的空间直角坐标系，
D0,0,0
� 1,0,0
B1,1,0 C0,1,0
则 ， ， ， ，
  
Ex,y,zz0 AB0,1,0 AE x1,y,z AD1,0,0
设 ，则 ， ， ，
   
ABAE  y AEAD1x
所以 ， ，
EAB60 EAD45
因为  ， ，
ABAE  AB  AE cosEAB12cos601 y1
所以 ，所以 ，
   
AEAD AE AD cosEAD 21cos45 2 1x 2 x1 2
因为 ，所以 ，解得 ，
数学参考答案（萍实版）-4
{#{QQABTYIEogiAAhAAAAhCAQFgCECQkhGCAYgGxEAMoAAASAFABCA=}#} A  E     2,1,z   A  E     2 2 12 z2 2
所以 ，则 ，

   
z  0 z1 AE   2,1,1 E 1 2,1,1
又 ，所以 ，所以 ， ，
AC FBCE EABCD
连接 ，因为三棱锥 的体积是四棱锥 体积的一半，
1 1
V  V  2V V V
所以 FBCE 2 EABCD 2 EABC EABC ABCE，
  
EF AB 0 AB BCE EF∥AB EF  AB1 EF 0,1,0 F  1 2,2,1  ,
又 ， 平面 ，所以 ，且 ，所以 ，

AEF
nx,y,z 
设平面 的法向量为 1 1 1 ，
 
 AEn 0  2x  y z 0   
则    E  F  n  0 ，得  y
1
0 1 1 1 ，取 x 1 1 ，则 n 1,0, 2 ，设点 C 到平面 AEF 的距离为 d ，
 
ACn
 1 3
AC 1,1,0 d     C AEF 3
因为 ，所以 n  2 3 ，即点 到平面 的距离为 ．
1202 2 3
  
AEF n 1,0, 2
由①知，平面 的一个法向量为 ，

BCF mx ,y ,z 
设平面 的法向量为 2 2 2 ，
   
BC 1,0,0 BF   2,1,1
易知 ， ，
   
 BCm0 x 0    nm  2 3
由    B  F  m  0 ，得   2 2x  y z 0，取 y 2 1 ，则 m0,1,1 ，所以 cosn,m n  m   3 2  3 ，
2 2 2
AEF BCF  sin 1cos2 1cos2n  ,m   1   3  2  6
设平面 与平面 所成二面角为 ， 则   ，
 3  3
6
AEF BCF
所以平面 与平面 所成二面角的正弦值为 ．
3
a 5 a 5 a 1
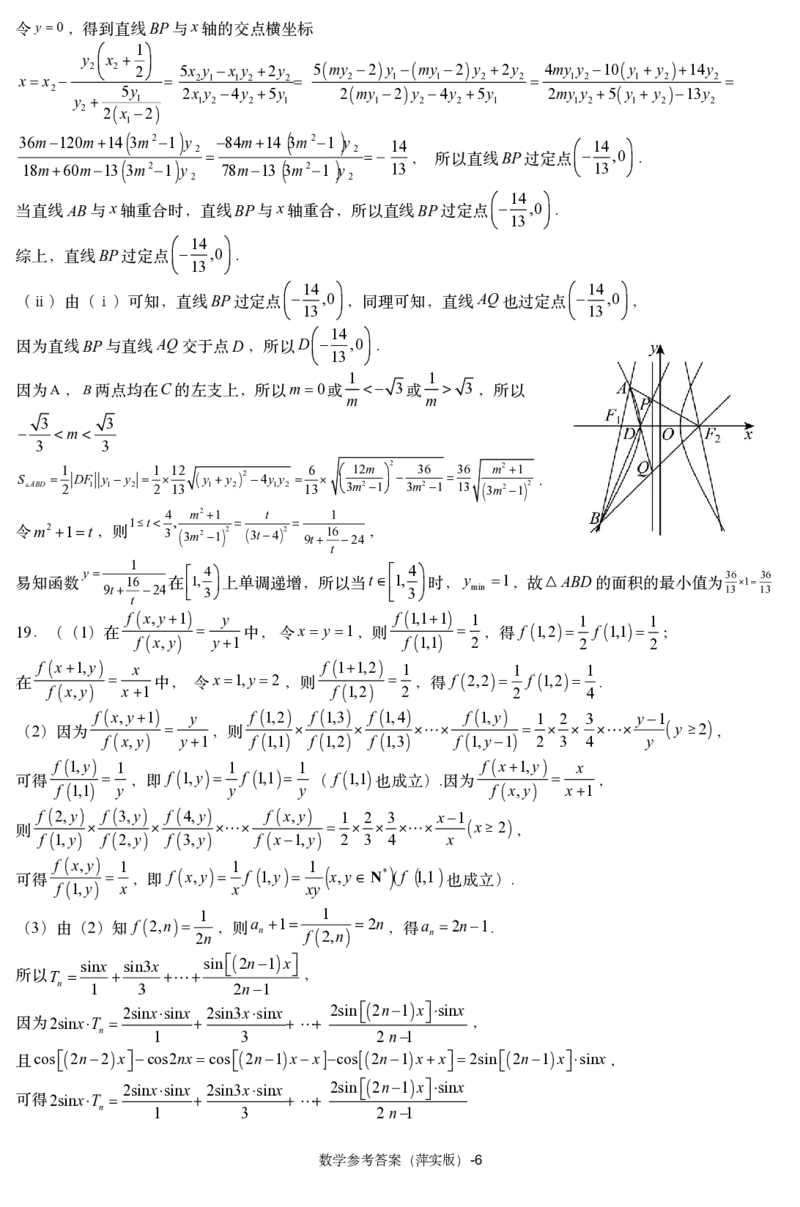
18 1 x  0 M l 2  
．（ ）因为 a2b2 ，且点 到直线 的距离为2，所以 a2b2 2，则 a2b2 2，所以
4 9
3a2 b2  1
，由题意可知a2 b2 ，
4 9 y2
3a2 b2  1 a2 1 b2 3 C x2 1
将 代入上式，得a2 3a2 ，解得 ，则 ，故双曲线 的标准方程为 3 ．
1
2 1 F 2,0,F 2,0,l:x
（ ）（ⅰ）由（ ）可知， 1 2 2．
AB x xmy2,Ax,y ,Bx ,y 
当直线 与 轴不重合时，设其方程为 1 1 2 2 ，
xmy2
  y2 x  3m21  y212my90
联立方程，得 x2 1，消去 ，化简整理得 ，
 3
 3m210
12m 9
 ,y y  ,y y 
则

Δ144m236  3m21 36  m21 0 1 2 3m21 1 2 3m21．
y
AF y 1 x2
易知直线 2的方程为 x 2 ，
1
x 2 AF x l x 2
当 1 时， 2 轴，与直线 平行，不相交，不符合题意，故 1 ，
1  1 5y 
令 x 2，得到点 P 的坐标为     2 , 2x 1  1 2    ，
 1  5y 
BP x   yy  y  1  xx 
所以直线 的方程为 2 2 2  2 2x
1
2  2 ．
数学参考答案（萍实版）-5
{#{QQABTYIEogiAAhAAAAhCAQFgCECQkhGCAYgGxEAMoAAASAFABCA=}#}y0 BP x
令 ，得到直线 与 轴的交点横坐标
 1
y 2   x 2  2   5x y x y 2y 5my 2y my 2y 2y 4my y 10y  y 14y
xx   2 1 1 2 2 2 1 1 2 2  1 2 1 2 2 
2 5y 2x y 4y 5y 2my 2y 4y 5y 2my y 5y  y 13y
y  1 1 2 2 1 1 2 2 1 1 2 1 2 2
2 2x 2
1
36m120m14  3m21  y 84m14  3m21  y 14  14 
18m60m13  3m21  y 2  78m13  3m21  y 2  13， 所以直线 BP 过定点    13 ,0 ．
2 2
 14 
AB x BP x BP  ,0
当直线 与 轴重合时，直线 与 轴重合，所以直线 过定点 13 ．
 14 
BP  ,0
综上，直线 过定点 13 ．
 14   14 
BP  ,0 AQ  ,0
（ⅱ）由（ⅰ）可知，直线 过定点 13 ，同理可知，直线 也过定点 13 ，
 14 
BP AQ D D ,0
因为直线 与直线 交于点 ，所以  13 ．
1 1
A B C m0  3  3
因为 ， 两点均在 的左支上，所以 或m 或m ，所以
3 3
 m
3 3
S  1 DF y y  1  12 y y 24yy  6    12m   2  36  36 m21
ABD 2 1 1 2 2 13 1 2 1 2 13 3m21 3m21 13  3m21 2 ．
4 m21 t 1
1t ,  
令 m21t ，则 3  3m21 2 3t42 9t 16 24，
t
1
易知函数 y 9t 16 24在    1, 4 3    上单调递增，所以当 t    1, 4 3    时， y min 1 ，故 △ABD 的面积的最小值为1 3 3 6 1 1 3 3 6
t
f x,y1 y f 1,11 1 1 1
19 1  x y1  f 1,2 f 1,1
．（（ ）在 f x,y y1中，令 ，则 f 1,1 2，得 2 2；
f x1,y x f 11,2 1 1 1
 x1,y2  f 2,2 f 1,2 .
在 f x,y x1中， 令 ，则 f 1,2 2 ，得 2 4
f x,y1 y f 1,2 f 1,3 f 1,4 f 1,y 1 2 3 y1
2         y 2
（ ）因为 f x,y y1，则 f 1,1 f 1,2 f 1,3 f 1,y1 2 3 4 y ，
f 1,y 1 1 1 f x1,y x
 f 1,y f 1,1 f 1,1 . 
可得 f 1,1 y ，即 y y （ 也成立）因为 f x,y x1，
f 2,y f 3,y f 4,y f x,y 1 2 3 x1
       x2
则 f 1,y f 2,y f 3,y f x1,y 2 3 4 x ，
f x,y  1 f x,y 1 f 1,y 1  x,y N* (f 1,1 .
可得 f 1,y x，即 x xy 也成立）
1 1
（ 3 ）由（ 2 ）知 f 2,n 2n ，则 a n 1 f 2,n 2n ，得 a n 2n1.
sinx sin3x
sin

2n1x

T   
所以 n 1 3 2n1 ，
2sinxsinx 2sin3xsinx 2sin  2n1x  sinx
2sinxT    
因为 n 1 3 2n1 ，
cos

2n2x

cos2nxcos

2n1xxcos2n1xx

2sin

2n1x

sinx
且 ，
2sinxsinx 2sin3xsinx 2sin  2n1x  sinx
2sinxT    
可得 n 1 3 2n1
数学参考答案（萍实版）-6
{#{QQABTYIEogiAAhAAAAhCAQFgCECQkhGCAYgGxEAMoAAASAFABCA=}#}cos2xcos4x cos4xcos6x cos  2n2x  cos2nx
1cos2x  
3 5 2n1
 1 1 1  1 1  cos2nx
11 cos2x  cos4x  cos  2n2x   .
 3 3 5 2n3 2n1 2n1
�∈ 0,π
2nx0,2nπ cos2x1,1,cos2nx1,1 
由 ，得 ，则 ，
 1 1 1  1 1  cos2 nx
则 2sinxT n 1  1 3   cos2x 3  5   cos4x  2n3  2n1   cos  2n2 x    2n1
 1 1 1  1 1  1
11      0 2sinxT 0 �∈ 0,π sinx0 T 0.
 3 3 5 2n3 2n1 2n1 ，即 n ，且 ，得 ，所以 n
数学参考答案（萍实版）-7
{#{QQABTYIEogiAAhAAAAhCAQFgCECQkhGCAYgGxEAMoAAASAFABCA=}#}