2006年湖南高考理科数学真题及答案_数学高考真题试卷_旧1990-2007·高考数学真题_1990-2007·高考数学真题·word_湖南

2006 年湖南高考理科数学真题及答案 一、选择题:本大题共10小题，每小题5分，共50分。在每个小题给出的四个选项中，只 有一项是符合题目要求的。 1. 函数 的定义域是 y  log x2 2 A． B． C． D． (3,) [3,) (4,) [4,) 1 2. 若数列{a }满足: a  , 且对任意正整数 m,n 都有a  a a , 则 n 1 3 mn m n lim(a a a )  1 2 n n 1 2 3 A． B． C． D．2 2 3 2 3. 过平行六面体 任意两条棱的中点作直线, 其中与平面 平 ABCD A BC D DBB D 1 1 1 1 1 1 行的直线共有 A．4条 B．6条 C．8条 D．12条 4. “ ”是“函数 在区间 上为增函数”的 a 1 f(x) | xa| [1,) A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 5. 已知 且关于 的方程 有实根, 则 与 的夹角 |a| 2|b| 0, x x2|a| xab  0 a b 的取值范围是    2  A．[0, ] B．[ ,] C．[ , ] D．[ ,] 6 3 3 3 6 6. 某外商计划在4个候选城市投资3个不同的项目, 且在同一个城市投资的项目不超过 2个, 则该外商不同的投资方案有 A． 16种 B．36种 C．42种 D．60种 7. 过双曲线 y2 的左顶点 作斜率为1的直线 , 若 与双曲线 的两条 M :x2  1 A l l M b2 渐近线分别相交于点 , 且 , 则双曲线 的离心率是 B,C | AB|| BC | M A． B． C． 10 D． 5 10 5 3 2 xa 8. 设函数 f(x)  , 集合M {x| f(x) 0},P {x| f (x) 0}, 若M  P, x1 则实数a的取值范围是 第1页 | 共15页A． B． C． D． (,1) (0,1) (1,) [1,) 9. 棱长为2的正四面体的四个顶点都在同一个球面上, 若过该球球心的一个截面如图 1, 图1 则图中三角形(正四面体的截面)的面积是 A． 2 B． 3 C． D． 2 3 2 2 10. 若圆 上至少有三个不同的点到直线 的 x2  y2 4x4y10  0 l:axby 0 距离为 ,则直线 的倾斜角的取值范围是 2 2 l    5    A． [ ， ] B．[ ， ] C．[ ， ] D．[0， ] 12 4 12 12 6 3 2 注意事项： 请用0.5毫米黑色的签字笔直接答在答题卡上。答在试题卷上无效。 二、填空题：本大题共5小题，每小题4分(第15小题每空2分)，共20分. 把答案 填在答题卡中对应题号后的横线上。 11. 若 的展开式中 的系数是 , 则实数 的值是__________. （ax1)5 x3 80 a x 1  12. 已知 x y10 则x2  y2的最小值是_____________.  2x y20  1 13. 曲线y  和y  x2在它们的交点处的两条切线与x轴所围成的三角形的面积是 x ___________.   14. 若 f(x)  asin(x )bsin(x )(ab  0)是偶函数, 则有序实数对(a,b)可以 4 4 是__________.(注: 写出你认为正确的一组数字即可) 15. 如图2, OM // AB, 点P在由射线OM , 线段OB及AB的延长线围成的区域内 (不含边界)运动, 且 ,则 的取值范围是__________; 当 OP  xOA yOB x 1 x   时, y 的取值范围是__________. 2 第2页 | 共15页P B M A O 图2 三、解答题：本大题共6小题，共80分，解答应写出文字说明，证明过程或演算步骤。 16. （本小题满分12分） 如图3, 是直角 斜边 上一点, . D ABC BC AB  AD,记CAD ,ABC  (Ⅰ)证明: ; (Ⅱ)若 ,求 的值. sincos20 AC  3DC  A B D C 图3 17. （本小题满分12分） 某安全生产监督部门对5家小型煤矿进行安全检查(简称安检), 若安检不合格, 则必须整 改. 若整改后经复查仍不合格, 则强制关闭. 设每家煤矿安检是否合格是相互独立的, 且 每家煤矿整改前合格的概率是0.5, 整改后安检合格的概率是0.8, 计算(结果精确到0.01); (Ⅰ) 恰好有两家煤矿必须整改的概率; (Ⅱ) 平均有多少家煤矿必须整改; (Ⅲ) 至少关闭一家煤矿的概率 . 18. （本小题满分14分） 如图4, 已知两个正四棱锥 的高分别为1和2, P ABCD与Q ABCD AB  4 (Ⅰ) 证明: ; (Ⅱ) 求异面直线 所成的角; PQ 平面ABCD AQ与PQ (Ⅲ) 求点 到平面 的距离. P QAD 第3页 | 共15页P D C A B Q 图4 19．（本小题满分14分） 已知函数 , 数列 满足: , f(x)  xsinx {a } 0 a 1 n 1,2,3, n 1 1 证明 (Ⅰ) 0 a  a 1 ; (Ⅱ) a  a3 . n1 n n1 6 n 20．（本小题满分14分） 对1个单位质量的含污物体进行清洗, 清洗前其清洁度(含污物体的清洁度定义为: 污物质量 为 , 要求清洗完后的清洁度为 . 有两种方案可供 1 ） 0.8 0.99 物体质量（含污物） 选择, 方案甲: 一次清洗; 方案乙: 分两次清洗. 该物体初次清洗后受残留水等因素 x0.8 影响, 其质量变为a(1 a 3). 设用x单位质量的水初次清洗后的清洁度是 x1 yac , 用 单位质量的水第二次清洗后的清洁度是 , (x  a1) y ya 其中 是该物体初次清洗后的清洁度. c (0.8c 0.99) (Ⅰ)分别求出方案甲以及c 0.95时方案乙的用水量, 并比较哪一种方案用水量较少; (Ⅱ)若采用方案乙, 当a为某固定值时, 如何安排初次与第二次清洗的用水量, 使总用 水量最小? 并讨论a取不同数值时对最少总用水量多少的影响. 21．（本小题满分14分） 已知椭圆 x2 y2 , 抛物线 , 且 的公共弦 C :  1 C :(ym)2  2px(p  0) C ,C 1 4 3 2 1 2 过椭圆 的右焦点 . AB C 1 第4页 | 共15页(Ⅰ) 当 , 求 的值, 并判断抛物线 的焦点是否在直线 上; AB  x轴时 m,p C AB 2 (Ⅱ) 是否存在 的值, 使抛物线 的焦点恰在直线 上? 若存在, 求出符合条 m,p C AB 2 件的m,p的值; 若不存在, 请说明理由 . 2006年湖南高考理科数学真题参考答案 1—10 DADAB DACCB 3 1 3 1. 2 2. 5 3. 4. (1,1) 15. (,0)，( , ) 4 2 2 1．函数 y  log x2 的定义域是 log x2≥0，解得x≥4，选D. 2 2 1 2 ． 数 列 {a }满 足 : a  , 且 对 任 意 正 整 数 m,n 都 有 a  a a n 1 3 mn m n 1 1 1 1 a a a a  ，a a a  a ，∴数列{a }是首项为 ，公比为 的等比数 2 11 1 1 9 n1 n 1 3 n n 3 3 a 1 列。 ，选A. lim(a a a )  1  n 1 2 n 1q 2 D 1 C 1 3．如图，过平行六面体 任意两条棱的中点作直 A ABCD A BC D 1 B1 1 1 1 1 D C 线, 其中与平面 平行的直线共有12条，选D. DBB D 1 1 A B 4．若“ ”，则函数 = 在区间 上为 a 1 f(x) | xa| |x1| [1,) 增函数；而若 在区间 上为增函数，则0≤a≤1，所以“ ”是 f(x) | xa| [1,) a 1 “函数 在区间 上为增函数”的充分不必要条件，选A. f(x) | xa| [1,)  5． 且关于 的方程 有实根，则 ，设 |a| 2|b| 0, x x2|a| xab  0 |a|2 4ab≥0 1   |a|2  ab 4 1  向量a,b的夹角为θ，cosθ=  ≤  ，∴θ∈[ ,]，选B. |a||b| 1  2 3 |a|2 2 6．某外商计划在4个候选城市投资3个不同的项目, 且在同一个城市投资的项目不超过2 个，则有两种情况，一是在两个城市分别投资1个项目、2个项目，此时有 种 C1A2 36 3 4 方案，二是在三个城市各投资1个项目，有 种方案，共计有60种方案，选D. A3 24 4 第5页 | 共15页7．过双曲线 y2 的左顶点 (1，0)作斜率为1的直线 ：y=x－1, 若 与双曲 M :x2  1 A l l b2 线 的两条渐近线 y2 分别相交于点 , 联立方程组代入消元 M x2  0 B(x ,y ),C(x ,y ) b2 1 1 2 2  2 x x  得 ，∴   1 2 1b2 ，x+x=2xx ，又 ,则B为AC (b2 1)x2 2x10  1 2 1 2 | AB|| BC | 1  x x   1 2 1b2  1 x  中点，2x=1+x，代入解得   1 4 ，∴ b=9，双曲线 的离心率e=c ，选A. 1 2  2 M  10 1 a  x   2 2 xa 8．设函数 f(x)  , 集合M {x| f(x)0}，若a>1时，M={x| 10，∴  P {x| f(x)0} f '(x) (x1)2 a>1时，P=R，a<1时，P=； 已知M  P,所以选C. 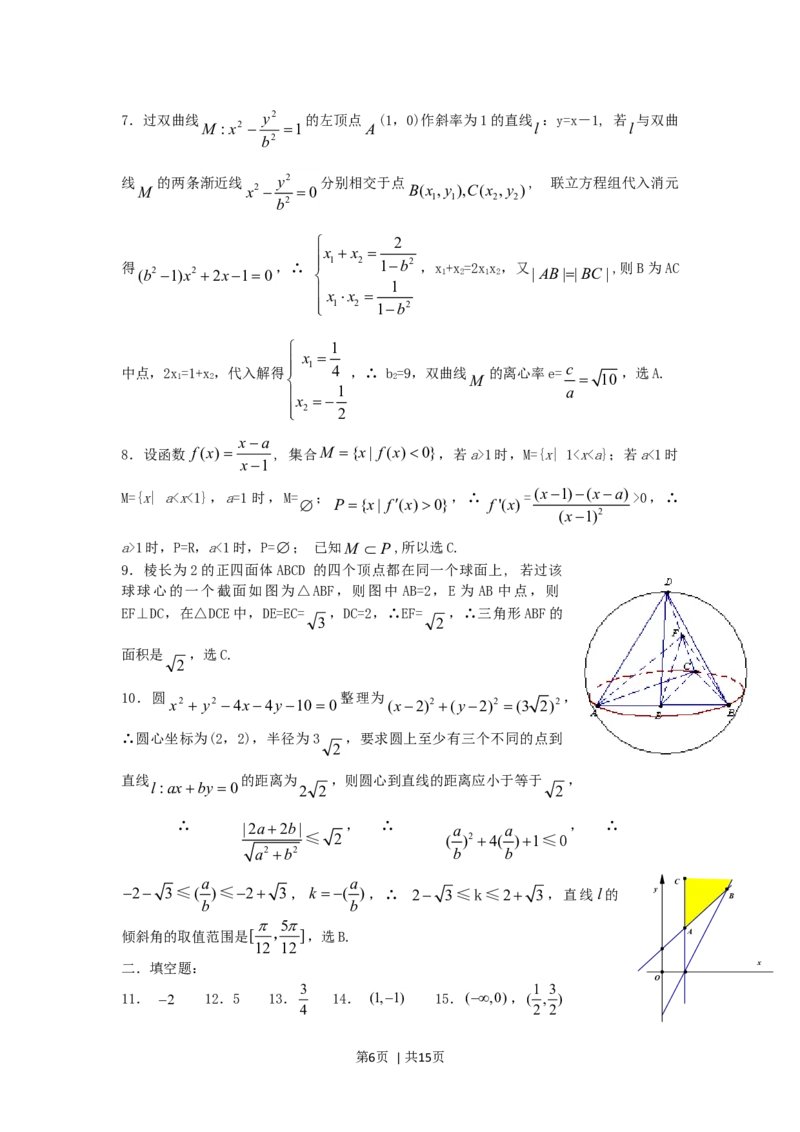9．棱长为2的正四面体ABCD 的四个顶点都在同一个球面上, 若过该 球球心的一个截面如图为△ABF，则图中 AB=2，E 为 AB 中点，则 EF⊥DC，在△DCE中，DE=EC= ，DC=2，∴EF= ，∴三角形ABF的 3 2 面积是 ，选C. 2 10．圆 整理为 ， x2  y2 4x4y10  0 (x2)2 (y2)2 (3 2)2 ∴圆心坐标为(2，2)，半径为3 ，要求圆上至少有三个不同的点到 2 直线 的距离为 ，则圆心到直线的距离应小于等于 ， l:axby 0 2 2 2 ∴ |2a2b| ， ∴ a a ， ∴ ≤ 2 ( )2 4( )1≤0 a2 b2 b b a a C 2 3≤( )≤2 3， k ( )，∴ 2 3≤k≤2 3，直线l的 y B b b  5 倾斜角的取值范围是[ ， ]，选B. 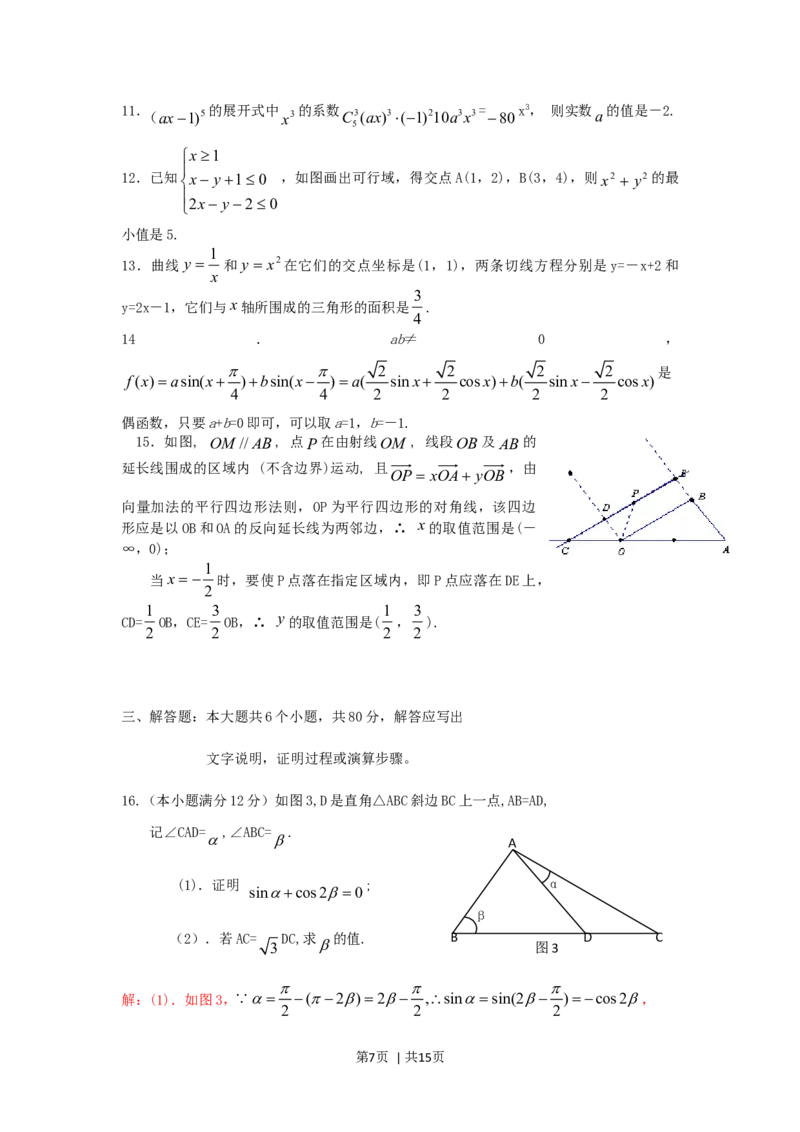A 12 12 二．填空题： x O 3 1 3 11． 2 12．5 13． 14． (1,1) 15．(,0)，( , ) 4 2 2 第6页 | 共15页11． 的展开式中 的系数 = x3， 则实数 的值是－2. （ax1)5 x3 C3(ax)3(1)210a3x3 80 a 5 x 1  12．已知 x y10 ，如图画出可行域，得交点A(1，2)，B(3，4)，则x2  y2的最  2x y20  小值是5. 1 13．曲线 y  和 y  x2在它们的交点坐标是(1，1)，两条切线方程分别是y=－x+2和 x 3 y=2x－1，它们与x轴所围成的三角形的面积是 . 4 14 ． ab≠ 0 ，   2 2 2 2 是 f(x)asin(x )bsin(x )a( sinx cosx)b( sinx cosx) 4 4 2 2 2 2 偶函数，只要a+b=0即可，可以取a=1，b=－1. 15．如图, OM // AB, 点P在由射线OM , 线段OB及AB的 延长线围成的区域内 (不含边界)运动, 且 ，由 OP  xOA yOB 向量加法的平行四边形法则，OP为平行四边形的对角线，该四边 形应是以OB和OA的反向延长线为两邻边，∴ x的取值范围是(－ ∞，0)； 1 当x   时，要使P点落在指定区域内，即P点应落在DE上， 2 1 3 1 3 y CD= OB，CE= OB，∴ 的取值范围是( ， ). 2 2 2 2 三、解答题：本大题共6个小题，共80分，解答应写出 文字说明，证明过程或演算步骤。 16.（本小题满分12分）如图3,D是直角△ABC斜边BC上一点,AB=AD, 记∠CAD= ,∠ABC= .   A (1)．证明 ; α sincos20 β （2）．若AC= DC,求 的值. B D C 3  图3    解：(1)．如图3， (2)2 ,sinsin(2 )cos2， 2 2 2 第7页 | 共15页即 ． sincos20 （2）．在ABC中，由正弦定理得 DC AC DC 3DC  ,  .sin 3sin sin sin() sin sin 由(1)得 ， sincos2 sin 3cos2 3(12sin2), 即 3 3 ． 2 3sin2sin 3 0.解得sin 或sin 2 3  3  0 ,sin , . 2 2 3 17.（本小题满分12分）某安全生产监督部门对5家小型煤矿进行安全检查(简称安检).若 安检不合格,则必须进行整改.若整改后经复查仍不合格,则强行关闭.设每家煤矿安检 是否合格是相互独立的,且每家煤矿整改前安检合格的概率是0.5, 整改后安检合格的 概率是0.8,计算(结果精确到0.01): (Ⅰ)恰好有两家煤矿必须整改的概率; (Ⅱ)平均有多少家煤矿必须整改; (Ⅲ)至少关闭一家煤矿的概率. 解：（Ⅰ）．每家煤矿必须整改的概率是1－0.5，且每家煤矿是否整改是相互独立的. 所以恰好有两家煤矿必须整改的概率是 5 P C2(10.5)20.53  0.31. 1 5 16 （Ⅱ）．由题设，必须整改的煤矿数 服从二项分布B(5,0.5).从而 的数学期望是   E ＝ ，即平均有2.50家煤矿必须整改.  50.52.5 (Ⅲ)．某煤矿被关闭，即该煤矿第一次安检不合格，整改后经复查仍不合格，所以该 煤矿被关闭的概率是P (10.5)(10.8)0.1，从而该煤矿不被关闭的概率是 2 0.9.由题意，每家煤矿是否被关闭是相互独立的，所以至少关闭一家煤矿的概率 是 P 10.95 0.41 3 18. （本小题满分14分）如图4,已知两个正四棱锥P-ABCD与Q-ABCD的高分别为1 和2,AB=4. (Ⅰ)证明PQ⊥平面ABCD; (Ⅱ)求异面直线AQ与PB所成的角; (Ⅲ)求点P到平面QAD的距离. 第8页 | 共15页P z P D C D C O A B B A x y Q Q 图 解法一： （Ⅰ）．连结AC、BD，设ACBDO.由P－ABCD与Q－ABCD 1 1 都是正四棱锥，所以PO⊥平面ABCD，QO⊥平面ABCD. 2 从而P、O、Q三点在一条直线上，所以PQ⊥平面ABCD. （ II）由题设知，ABCD是正方形，所以 AC BD．由（I），PQ平面 ABCD，故可以分别以直线CA、DB、QP为x轴， y轴，z轴建立空间直角坐标系 （如上4图），由题设条件，相关各点的坐标分别是 P(0,0,1)， Q(0,0,2)， B(0,2 42,0) 4   4    AQPB 3 所以 AQ(2 2,0,2) ,PB (0,2 2,1),于是cos AQ,PB    . AQ  PB 9 从而异面直线AQ与PB所成的角是 3 . arccos 9 (Ⅲ)．由（Ⅱ），点D的坐标是（0，－ ，0）， ， 2 2 AD(2 2,2 2,0)  ，设 是平面QAD的一个法向量， PQ(0,0,3) n(x,y,z) 由 nAQ0 得 2xz0 .   nAD0 xy0 取x=1，得 . 所以点P到平面QAD的距 n(1,1, 2)  P  PQn 3 2 离d    .. n 2 D C O 解法二： （Ⅰ）．取AD的中点M，连结PM，QM.因为P－ M B A ABCD与Q－ABCD 都是正四棱锥，所以AD⊥PM，AD⊥QM. 从 而AD⊥平面PQM. 又 PQ平面 PQM，所以 PQ⊥AD.同理 Q 第9页 | 共15页PQ⊥AB，所以PQ⊥平面ABCD. （Ⅱ）．连结AC、BD设ACBDO，由PQ⊥平面ABCD及正四棱锥的性质可知O在 PQ上，从而P、A、Q、C四点共面. 取OC的中点N，连结PN． PO 1 NO NO 1 PO NO 因为 ，所以 ，  ,    OQ 2 OA OC 2 OQ OA 从而AQ∥PＮ.∠BPＮ（或其补角）是异面直线AQ 与PB所成的角.连接BN， 因为 ． PB OB2OP2  (2 2)213 PN  ON2OP2  ( 2)21 3 BN  OB2ON2  (2 2)2( 2)2  10 PB2 PN2 BN2 9310 3 所以 ． cosBPN    2PBPN 23 3 9 从而异面直线AQ与PB所成的角是 3 ． arccos 9 (Ⅲ)．由（Ⅰ）知，AD⊥平面PＱM，所以平面PＱM⊥平面QAD. 过Ｐ作ＰＨ⊥ＱＭ 于Ｈ，则ＰＨ⊥平面QAD，所以ＰＨ的长为点P到平面QAD的距离． 1 连结OM，则OM  AB2OQ.所以MQP 45， 2 又ＰＱ＝ＰＯ＋ＱＯ＝３，于是 3 2 . PH  PQsin45  2 即点P到平面QAD的距离是3 2 . 2 19. （本小题满分14分）已知函数 , f(x) xsinx 数列{ }满足: a 0a 1,a  f(a ),n1,2,3,. n 1 n1 n 证明: （I）． ; 0a a 1 n1 n 1 （II）．a  a 3. n1 6 n 证明: （I）．先用数学归纳法证明 ，ｎ＝1,2,3,… 0a 1 n (i).当n=1时,由已知显然结论成立. 第10页 | 共15页(ii).假设当n=k时结论成立,即 .因为00成立.于是g(a )0,即sina a  a 3 0． n n n 6 n 1 故a  a 3． n1 6 n 20. （本小题满分14分）对1个单位质量的含污物体进行清洗,清洗前其清洁度(含污物体 污物质量 的清洁度定义为: )为0.8,要求洗完后的清洁度是0.99.有两 1 物体质量(含污物) 种方案可供选择,方案甲:一次清洗;方案乙:两次清洗.该物体初次清洗后受残留水等因 x0.8 素影响,其质量变为a(1≤a≤3).设用x单位质量的水初次清洗后的清洁度是 ( x1 yac ),用 质量的水第二次清洗后的清洁度是 ,其中 是 xa1 y c(0.8c0.99) ya 该物体初次清洗后的清洁度. (Ⅰ)分别求出方案甲以及c0.95时方案乙的用水量,并比较哪一种方案用水量较少; (Ⅱ)若采用方案乙,当a为某定值时,如何安排初次与第二次清洗的用水量,使总用水量最少? 并讨论a取不同数值时对最少总用水量多少的影响. x0.8 解：(Ⅰ)设方案甲与方案乙的用水量分别为x与z,由题设有 =0.99,解得x=19. x1 由c0.95得方案乙初次用水量为3, 第二次用水量y满足方程: 第11页 | 共15页y0.95a 解得y=4 ,故z=4 +3.即两种方案的用水量分别为19与4 +3. 0.99, a a a ya 因为当 ,故方案乙的用水量较少. 1a3时,xz 4(4a)0,即x z （II）设初次与第二次清洗的用水量分别为x与 y ，类似（I）得 5c4 x ，ya(99100c)（*） 5(1c) 5c4 1 于是x y +a(99100c)  100a(1c)a1 5(1c) 5(1c) 1 当a为定值时, x y2 100a(1c)a1a4 5a 1 , 5(1c) 1 当且仅当 时等号成立.此时 100a(1c) 5(1c) 1 1 c1 (不合题意, 舍去)或c1 (0.8,0.99), 10 5a 10 5a 1 将 代入（*）式得 c1 x2 5a 1a1,y 2 5a a. 10 5a 1 故 时总用水量最少, 此时第一次与第二次用水量分别为 c1 10 5a , 最少总用水量是 . 2 5a 1与2 5a a T(a)a4 5a 1 2 5 当 ,故T( )是增函数(也可以用二次函数的单 1a3时,T'(a) 10 a a 调性判断).这说明,随着a的值的最少总用水量, 最少总用水量最少总用水量. 21. （本小题满分14分）已知椭圆C: x2 y2 ,抛物线C: , 1  1 2 (ym)2 2px(p 0) 4 3 且C、C 的公共弦AB过椭圆C 的右焦点. 1 2 1 (Ⅰ)当AB⊥x轴时,求m、 p的值，并判断抛物线C 的焦点是否在直线AB上； 2 (Ⅱ)是否存在m、 p的值，使抛物线C 的焦点恰在直线AB上？若存在， 2 求出符合条件的m、 p的值；若不存在，请说明理由. 解：（Ⅰ）当AB⊥x轴时，点A、B关于x轴对称，所以m＝0，直线AB的方程为： 3 3 x =1，从而点A的坐标为（1， ）或（1，－ ）. 因为点A在抛物线上. 2 2 第12页 | 共15页9 9 9 所以 2p，即 p .此时C 2 的焦点坐标为（ ，0），该焦点不在直线AB上. 4 8 16 （II）解法一： 假设存在 、 的值使 的焦点恰在直线AB上，由（I）知直线AB m p C 2 的斜率存在，故可设直线AB的方程为yk(x1)． yk(x1) 由 消去 得 ………………① x2 y2 y (34k2)x28k2x4k2120   1  4 3 y 设A、B的坐标分别为（x,y）, （x,y）, 1 1 2 2 A 8k2 则x,x是方程①的两根，x＋x＝ . 1 2 1 2 34k2 O x (ym)2 2px 由  B y k(x1) 消去y得 . ………………② (kxkm)2 2px p 因为C的焦点F( ,m)在直线yk(x1)上， 2 2 p kp kp 所以mk( 1)，即mk  .代入②有(kx )2 2px. 2 2 2 即 k2p2 . …………………③ k2x2  p(k2 2)x 0 4 由于x,x也是方程③的两根，所以x＋x＝ p(k2 2) . 1 2 1 2 k2 从而 8k2 ＝ p(k2 2) . 解得 8k2 ……………………④ p 34k2 k2 (4k2 3)(k2 2) 又AB过C C的焦点，所以 1、、＼、、 2 p p 1 1 AB (x  )(x  ) x x  p(2 x )(2 x )， 1 2 2 2 1 2 2 1 2 2 则 3 12k2 4k2 12 …………………………………⑤ p4 (x x )4  . 2 1 2 4k2 3 4k2 3 8k2 4k2 12 由④、⑤式得 ，即 ．  k4 5k2 60 (4k2 3)(k2 2) 4k2 3 4 解得k2 6.于是k  6,p . 3 第13页 | 共15页2 2 因为C的焦点F( ,m)在直线y  6(x1)上，所以m 6( 1). 2 3 3 6 6  m 或m ． 3 3 6 6 4 由上知，满足条件的m、 p 存在，且m 或m ， p ． 3 3 3 解法二： 设A、B的坐标分别为 ， ． (x,y ) (x y ) 1 1 2 2 p 因为AB既过C的右焦点F(1,0)，又过C的焦点F( ,m)， 1 2 2 p p 1 1 所以 AB (x  )(x  )x x  p(2 x )(2 x ). 1 2 1 2 1 2 2 2 2 2 2 即x x  (4 p). ……① 1 2 3 y  y m0 2m k  2 1   由（Ⅰ）知x  x ,p 2，于是直线AB的斜率 x x p p2， …… 1 2 2 1 1 2 ② 2m 且直线AB的方程是 , y  (x1) p2 2m 4m(1 p) 所以 . ……③ y  y  (x x 2) 1 2 p2 1 2 3(p2) 又因为  3x 1 2 4y 1 2 12 ，所以 3(x 1 x 2 )4(y 1 y 2 ) y 2 y 1 0 . ……④ 3x 2 2 4y 2 2 12 x 2 x 1 3(p4)(p2)2 将①、②、③代入④得 ． ……………⑤ m2  16(1 p) (y m)2 2px x x 因为 1 1 ，所以y  y 2m2p 2 1 ． …………⑥   (y 2 m)2 2px 2 1 2 y 2  y 1 3p(p2)2 将②、③代入⑥得 ……………⑦ m2  . 1610p 3(p4)(p2)2 3p(p2)2 由⑤、⑦得 即  . 3p2 20p320 16(1 p) 1610p 4 4 2 解得 p 或p8(舍去)．将 p 代入⑤得m2  , 3 3 3 第14页 | 共15页6 6  m 或m ． 3 3 6 6 4 由上知，满足条件的m、 p 存在，且m 或m ， p 3 3 3 第15页 | 共15页