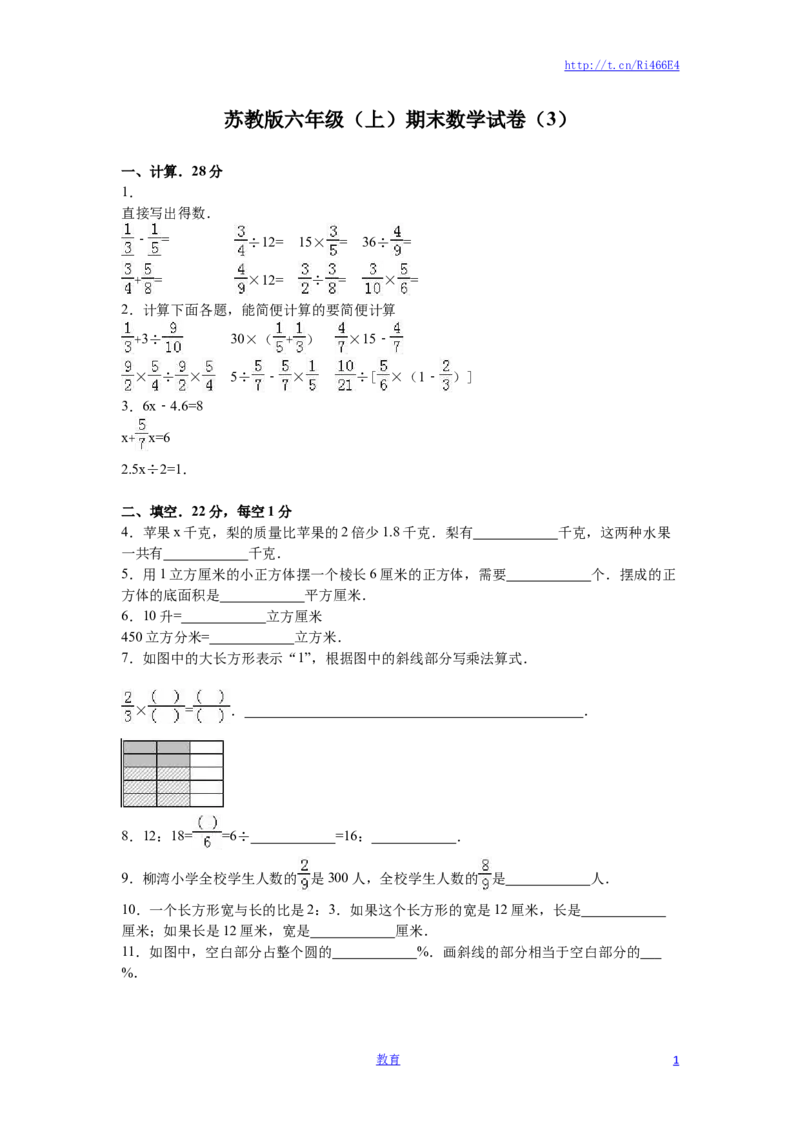文档内容
http://t.cn/Ri466E4
苏教版六年级(上)期末数学试卷(3)
一、计算.28分
1.
直接写出得数.
﹣ = ÷12= 15× = 36÷ =
+ = ×12= ÷ = × =
2.计算下面各题,能简便计算的要简便计算
+3÷ 30×( + ) ×15﹣
× ÷ × 5÷ ﹣ × ÷[ ×(1﹣ )]
3.6x﹣4.6=8
x+ x=6
2.5x÷2=1.
二、填空.22分,每空1分
4.苹果x千克,梨的质量比苹果的2倍少1.8千克.梨有 千克,这两种水果
一共有 千克.
5.用1立方厘米的小正方体摆一个棱长6厘米的正方体,需要 个.摆成的正
方体的底面积是 平方厘米.
6.10升= 立方厘米
450立方分米= 立方米.
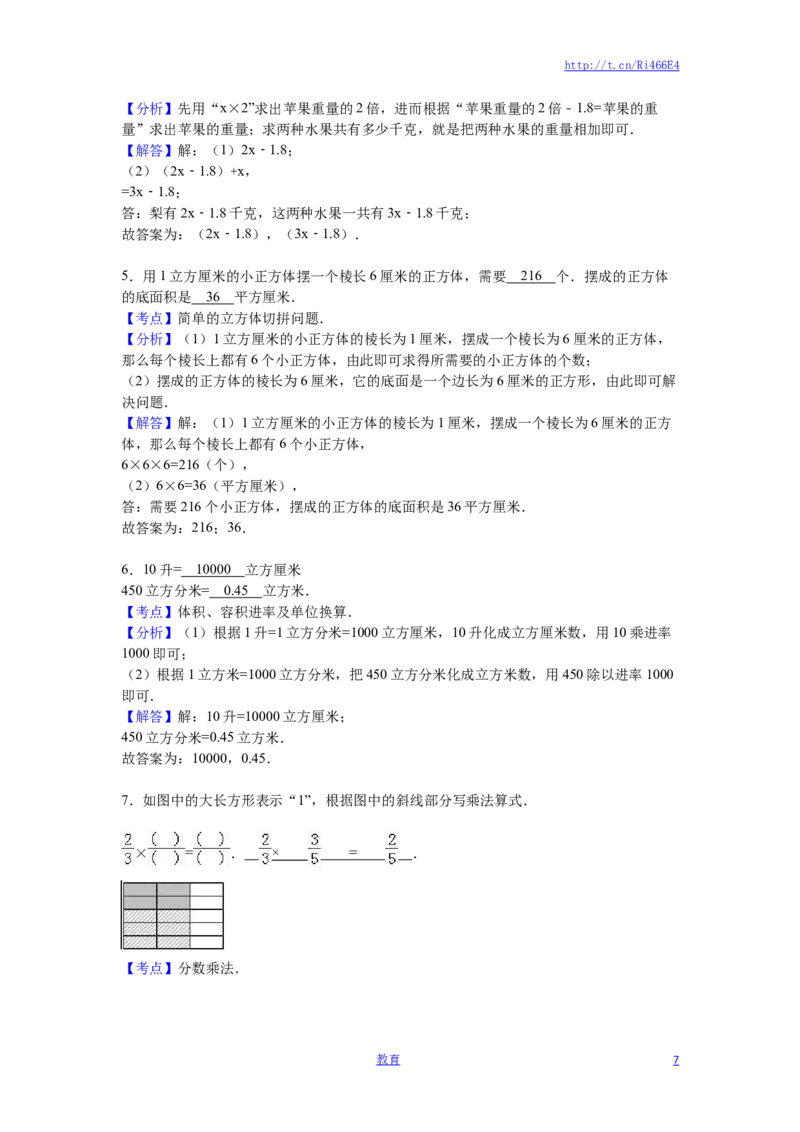
7.如图中的大长方形表示“1”,根据图中的斜线部分写乘法算式.
× = . .
8.12:18= =6÷ =16: .
9.柳湾小学全校学生人数的 是300人,全校学生人数的 是 人.
10.一个长方形宽与长的比是2:3.如果这个长方形的宽是12厘米,长是
厘米;如果长是12厘米,宽是 厘米.
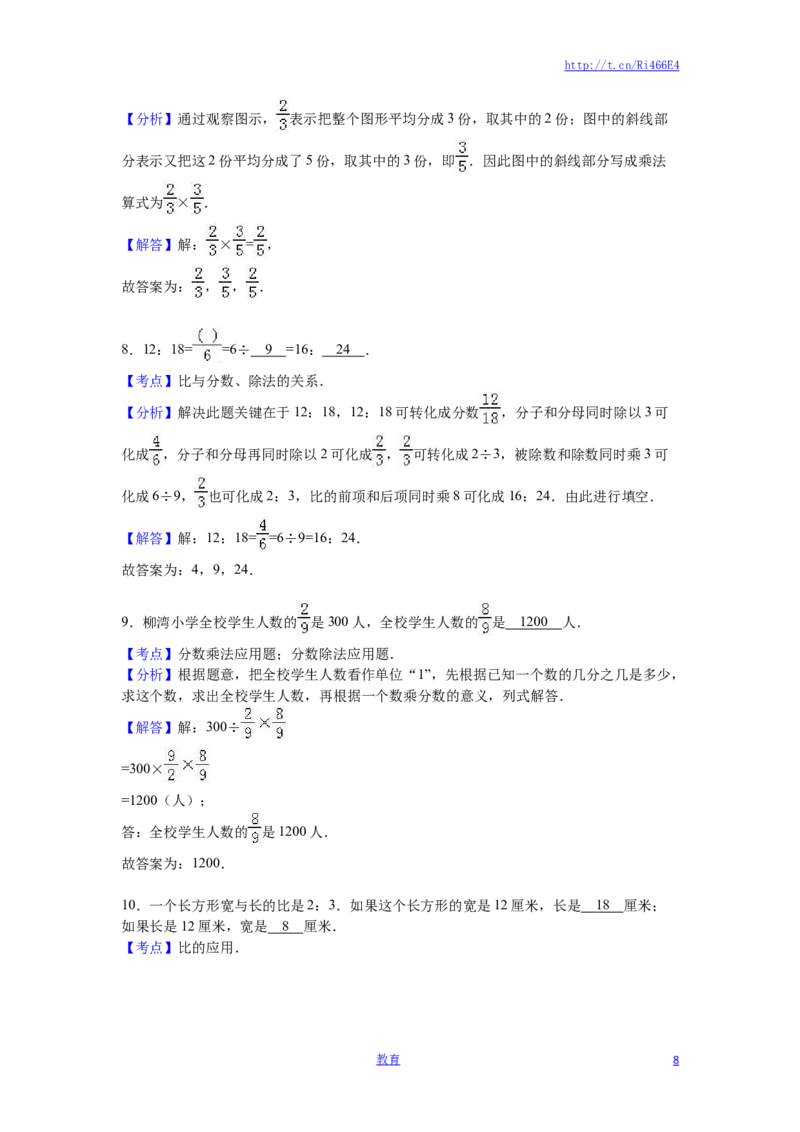
11.如图中,空白部分占整个圆的 %.画斜线的部分相当于空白部分的
%.
教育 1http://t.cn/Ri466E4
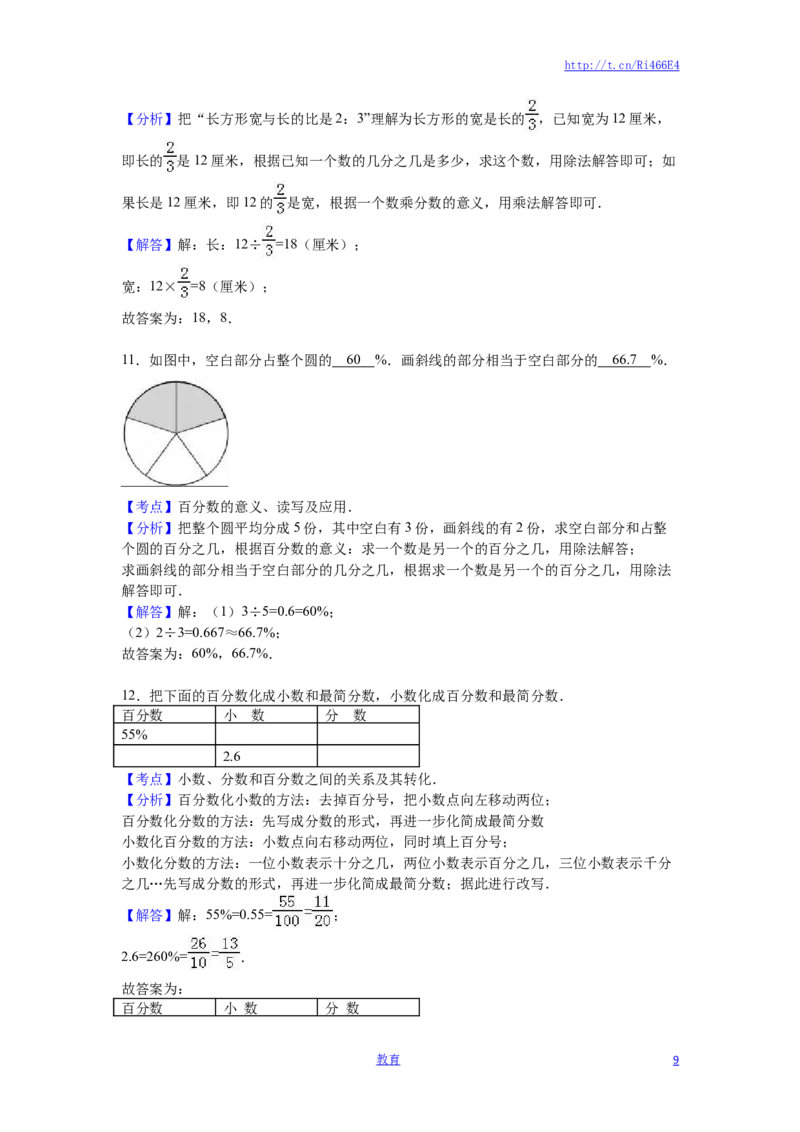
12.把下面的百分数化成小数和最简分数,小数化成百分数和最简分数.
百分数 小 数 分 数
55%
2.6
13.把1~9九张数字卡片打乱后反扣在桌上,从中任意抽出一张,用分数表示下面各种情
况出现的可能性有多大.
抽到5的可能性是 ;抽到偶数的可能性是 ;抽到比8小的数的
可能性是 .
三、选择合适的答案,8分,每题1分
14.红球有20个,蓝球的个数比红球多 .算式20× 求的是( )
A.蓝球有几个 B.蓝球比红球多几个
C.两种球一共有几个
15.用小棒搭一个长和宽都是4厘米,高7厘米的长方体模型,需要长4厘米的小棒(
)根.
A.4根 B.8根 C.12根
16.在一个装满水的正方体容器里,放入2块各是400立方厘米的铁块,使铁块完全浸没
在水中,容器里的水至少会溢出( )
A.200立方厘米 B.400立方厘米 C.800立方厘米
17.小民和小林进行投篮练习.小民的命中率是75%,小林的命中率是80%.谁投中的次
数多些?( )
A.小民多些□ B.小林多些□
C.可能小民多,也可能小林多□
18.纺织厂男职工人数是女职工人数的 ,女职工人数是全厂职工人数的几分之几?(
)
A. B. C.
19.三个连续的偶数中,最小的一个是a,最大的一个是几?( )
A.a+2 B.a+4 C.3a
20.用一根长100厘米的绳子围一个长方形,使长与宽的比是7:3.这个长方形的宽是(
)
A.35厘米 B.30厘米 C.15厘米
21.一杯盐水,水与盐的比是10:1.这杯盐水的含盐率大约是( )
A.9.09% B.10% C.11%
四、按照要求画图.9分
教育 2http://t.cn/Ri466E4
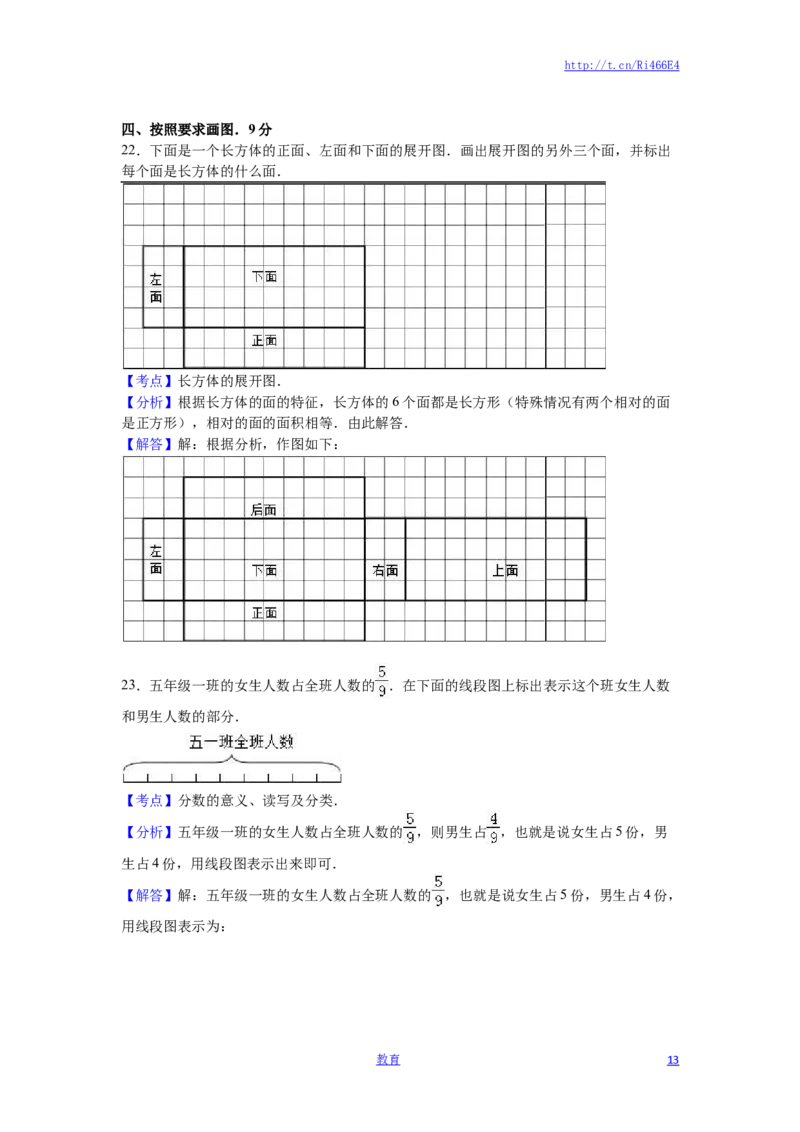
22.下面是一个长方体的正面、左面和下面的展开图.画出展开图的另外三个面,并标出
每个面是长方体的什么面.
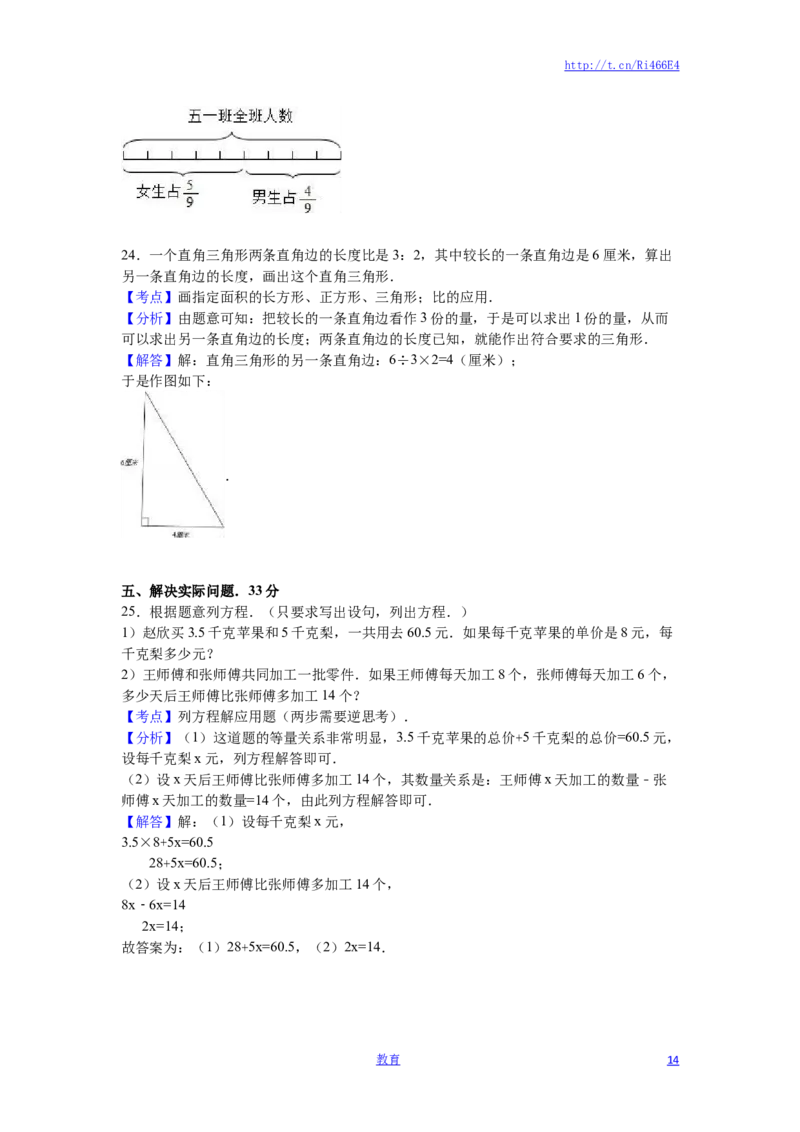
23.五年级一班的女生人数占全班人数的 .在下面的线段图上标出表示这个班女生人数
和男生人数的部分.
24.一个直角三角形两条直角边的长度比是3:2,其中较长的一条直角边是6厘米,算出
另一条直角边的长度,画出这个直角三角形.
五、解决实际问题.33分
25.根据题意列方程.(只要求写出设句,列出方程.)
1)赵欣买3.5千克苹果和5千克梨,一共用去60.5元.如果每千克苹果的单价是8元,每
千克梨多少元?
2)王师傅和张师傅共同加工一批零件.如果王师傅每天加工8个,张师傅每天加工6个,
多少天后王师傅比张师傅多加工14个?
26.一台拖拉机昨天上午耕地4800平方米,下午耕地的面积是上午的 .这台拖拉机昨天
一共耕地多少平方米?
27.李林有120张邮票,相当于陆红的 .陆红有多少张邮票?
28.东林小学一共有学生1600人.六年级有200人,其中女生98人.六年级学生占全校
学生数的百分之几?六年级男生人数占全年级学生数的百分之几?
29.一个长方体沙坑的长6米,宽4米,深0.8米.挖这个沙坑一共要挖出多少立方米的泥
土?如果要在沙坑的四周抹水泥,抹水泥的面积是多少平方米?
30.王老师买了8个网球和1个足球,正好用去360元.足球的单价是网球的4倍,足球
和网球的单价各是多少元?
教育 3http://t.cn/Ri466E4
苏教版六年级(上)期末数学试卷(3)
参考答案与试题解析
一、计算.28分
1.
直接写出得数.
﹣ = ÷12= 15× = 36÷ =
+ = ×12= ÷ = × =
【考点】分数的加法和减法.
【分析】按照分数四则计算的计算法则直接计算得出答案即可.
【解答】
解: ﹣ = ÷12= 15× =9 36÷ =81
+ = ×12= ÷ =4 × =
2.计算下面各题,能简便计算的要简便计算
+3÷ 30×( + ) ×15﹣
× ÷ × 5÷ ﹣ × ÷[ ×(1﹣ )]
【考点】整数、分数、小数、百分数四则混合运算.
【分析】① +3÷ ,先算除法,再算加法;
②30×( + ),运用乘法分配律简算;
③ ×15﹣ ,运用乘法分配律简算;
④ × ÷ × ,把除数转化为乘它的倒数,再运用乘法交换律和结合律简算;
⑤5÷ ﹣ × ,先算除法、乘法、再算减法;
⑥ ÷[ ×(1﹣ )],先算小括号里面的减法,再算中括号里面的乘法,最后算除法.
【解答】解:① +3÷
=
=
教育 4http://t.cn/Ri466E4
= ;
②30×( + )
=
=6+10
=16;
③ ×15﹣
=
=
=8;
④ × ÷ ×
=
=
= ;
⑤5÷ ﹣ ×
=
=7
= ;
⑥ ÷[ ×(1﹣ )]
= [ ]
=
教育 5http://t.cn/Ri466E4
=
= .
3.6x﹣4.6=8
x+ x=6
2.5x÷2=1.
【考点】方程的解和解方程.
【分析】(1)根据等式性质,两边同加上4.6,变成6x=12.6,两边再同除以6即可;
(2)先运用乘法分配律的逆运算,把原式变为(1+ )x=6,即 x=6,然后根据等式性
质,两边同除以 即可;
(3)根据等式性质,两边同乘2,变为2.5x=2,再同除以2.5即可.
【解答】解:(1)6x﹣4.6=8,
6x﹣4.6+4.6=8+4.6,
6x=12.6,
6x÷6=12.6÷6,
x=2.1;
(2)x+ x=6,
(1+ )x=6,
x=6,
x÷ =6÷ ,
x=6× ,
x= ;
(3)2.5x÷2=1,
2.5x÷2×2=1×2,
2.5x=2,
2.5x÷2.5=2÷2.5,
x=0.8.
二、填空.22分,每空1分
4.苹果x千克,梨的质量比苹果的2倍少1.8千克.梨有 ( 2x﹣1. 8 ) 千克,这两种水
果一共有 ( 3x﹣1. 8 ) 千克.
【考点】用字母表示数.
教育 6http://t.cn/Ri466E4
【分析】先用“x×2”求出苹果重量的2倍,进而根据“苹果重量的2倍﹣1.8=苹果的重
量”求出苹果的重量;求两种水果共有多少千克,就是把两种水果的重量相加即可.
【解答】解:(1)2x﹣1.8;
(2)(2x﹣1.8)+x,
=3x﹣1.8;
答:梨有2x﹣1.8千克,这两种水果一共有3x﹣1.8千克;
故答案为:(2x﹣1.8),(3x﹣1.8).
5.用1立方厘米的小正方体摆一个棱长6厘米的正方体,需要 21 6 个.摆成的正方体
的底面积是 3 6 平方厘米.
【考点】简单的立方体切拼问题.
【分析】(1)1立方厘米的小正方体的棱长为1厘米,摆成一个棱长为6厘米的正方体,
那么每个棱长上都有6个小正方体,由此即可求得所需要的小正方体的个数;
(2)摆成的正方体的棱长为6厘米,它的底面是一个边长为6厘米的正方形,由此即可解
决问题.
【解答】解:(1)1立方厘米的小正方体的棱长为1厘米,摆成一个棱长为6厘米的正方
体,那么每个棱长上都有6个小正方体,
6×6×6=216(个),
(2)6×6=36(平方厘米),
答:需要216个小正方体,摆成的正方体的底面积是36平方厘米.
故答案为:216;36.
6.10升= 1000 0 立方厘米
450立方分米= 0.4 5 立方米.
【考点】体积、容积进率及单位换算.
【分析】(1)根据1升=1立方分米=1000立方厘米,10升化成立方厘米数,用10乘进率
1000即可;
(2)根据1立方米=1000立方分米,把450立方分米化成立方米数,用450除以进率1000
即可.
【解答】解:10升=10000立方厘米;
450立方分米=0.45立方米.
故答案为:10000,0.45.
7.如图中的大长方形表示“1”,根据图中的斜线部分写乘法算式.
× = . × = .
【考点】分数乘法.
教育 7http://t.cn/Ri466E4
【分析】通过观察图示, 表示把整个图形平均分成3份,取其中的2份;图中的斜线部
分表示又把这2份平均分成了5份,取其中的3份,即 .因此图中的斜线部分写成乘法
算式为 × .
【解答】解: × = ,
故答案为: , , .
8.12:18= =6÷ 9 =16: 2 4 .
【考点】比与分数、除法的关系.
【分析】解决此题关键在于12:18,12:18可转化成分数 ,分子和分母同时除以3可
化成 ,分子和分母再同时除以2可化成 , 可转化成2÷3,被除数和除数同时乘3可
化成6÷9, 也可化成2:3,比的前项和后项同时乘8可化成16:24.由此进行填空.
【解答】解:12:18= =6÷9=16:24.
故答案为:4,9,24.
9.柳湾小学全校学生人数的 是300人,全校学生人数的 是 120 0 人.
【考点】分数乘法应用题;分数除法应用题.
【分析】根据题意,把全校学生人数看作单位“1”,先根据已知一个数的几分之几是多少,
求这个数,求出全校学生人数,再根据一个数乘分数的意义,列式解答.
【解答】解:300÷
=300×
=1200(人);
答:全校学生人数的 是1200人.
故答案为:1200.
10.一个长方形宽与长的比是2:3.如果这个长方形的宽是12厘米,长是 1 8 厘米;
如果长是12厘米,宽是 8 厘米.
【考点】比的应用.
教育 8http://t.cn/Ri466E4
【分析】把“长方形宽与长的比是2:3”理解为长方形的宽是长的 ,已知宽为12厘米,
即长的 是12厘米,根据已知一个数的几分之几是多少,求这个数,用除法解答即可;如
果长是12厘米,即12的 是宽,根据一个数乘分数的意义,用乘法解答即可.
【解答】解:长:12÷ =18(厘米);
宽:12× =8(厘米);
故答案为:18,8.
11.如图中,空白部分占整个圆的 6 0 %.画斜线的部分相当于空白部分的 66. 7 %.
【考点】百分数的意义、读写及应用.
【分析】把整个圆平均分成5份,其中空白有3份,画斜线的有2份,求空白部分和占整
个圆的百分之几,根据百分数的意义:求一个数是另一个的百分之几,用除法解答;
求画斜线的部分相当于空白部分的几分之几,根据求一个数是另一个的百分之几,用除法
解答即可.
【解答】解:(1)3÷5=0.6=60%;
(2)2÷3=0.667≈66.7%;
故答案为:60%,66.7%.
12.把下面的百分数化成小数和最简分数,小数化成百分数和最简分数.
百分数 小 数 分 数
55%
2.6
【考点】小数、分数和百分数之间的关系及其转化.
【分析】百分数化小数的方法:去掉百分号,把小数点向左移动两位;
百分数化分数的方法:先写成分数的形式,再进一步化简成最简分数
小数化百分数的方法:小数点向右移动两位,同时填上百分号;
小数化分数的方法:一位小数表示十分之几,两位小数表示百分之几,三位小数表示千分
之几…先写成分数的形式,再进一步化简成最简分数;据此进行改写.
【解答】解:55%=0.55= ;
2.6=260%= .
故答案为:
百分数 小 数 分 数
教育 9http://t.cn/Ri466E4
55% 0.55
260% 2.6
13.把1~9九张数字卡片打乱后反扣在桌上,从中任意抽出一张,用分数表示下面各种情
况出现的可能性有多大.
抽到5的可能性是 ;抽到偶数的可能性是 ;抽到比8小的数的可能性是
.
【考点】简单事件发生的可能性求解.
【分析】共有9个数字,其中5有1张,偶数有2,4,6,8共4张,比8小的数有1﹣7共
7张,根据可能性的求法:即求一个数是另一个数的几分之几,用除法分别进行解答即可.
【解答】解:抽到5的可能性是:1÷9= ;
抽到偶数的可能性是:4÷9= ;
抽到比8小的数的可能性是:7÷9= ;
故答案为: , , .
三、选择合适的答案,8分,每题1分
14.红球有20个,蓝球的个数比红球多 .算式20× 求的是( )
A.蓝球有几个 B.蓝球比红球多几个
C.两种球一共有几个
【考点】分数乘法应用题.
【分析】根据“蓝球的个数比红球多 ,”知道 的单位“1”是红球的个数,即蓝球的个
数比红球多的占红球的 ,用20× ,就是求的蓝球比红球多的个数.
【解答】解:根据算式20× ,知道是求20的 是多少,
而20是红球的个数, 是蓝球的个数比红球多的分率,
所以,20× 是求蓝球比红球多的个数;
故选:B.
15.用小棒搭一个长和宽都是4厘米,高7厘米的长方体模型,需要长4厘米的小棒(
)根.
A.4根 B.8根 C.12根
【考点】长方体的特征.
教育 10http://t.cn/Ri466E4
【分析】根据长方体的特征,长方体的12条棱,分为3组,每组互相平行的一组4条棱的
长度相等,已知搭成的长方体的长和宽都是4厘米,高7厘米,因此需要4厘米的小棒8
根,因此解答.
【解答】解:根据长方体的棱的特征,一般情况12条棱分为3组(即长、宽、高),每组
4条棱的长度相等,由于长方体的长和宽都是4厘米,因此需要4厘米的小棒8根.
答:需要长4厘米的小棒8根.
故选:B.
16.在一个装满水的正方体容器里,放入2块各是400立方厘米的铁块,使铁块完全浸没
在水中,容器里的水至少会溢出( )
A.200立方厘米 B.400立方厘米 C.800立方厘米
【考点】探索某些实物体积的测量方法.
【分析】因为石块完全浸没在水中,所以溢出的水的体积就等于2块石块的体积.
【解答】解:400×2=800(立方厘米),
故选:C.
17.小民和小林进行投篮练习.小民的命中率是75%,小林的命中率是80%.谁投中的次
数多些?( )
A.小民多些□ B.小林多些□
C.可能小民多,也可能小林多□
【考点】百分率应用题.
【分析】因为小民和小林投篮的次数不一定,所以不能确定谁投中的次数多.
【解答】解:假如他们共投了20次,根据小民的命中率,他应投中20×75%=13(次),
小林投中了20×80%=16(次),则小林的命中率高;
如果小民共投了20次,小林共投了10次,则小民投中了20×75%=13(次),小林投中了
10×80%=8(次),则小民投中的次数多些;
因此可能小民投中的次数多些,也可能小林投中的次数多些.
故选:C.
18.纺织厂男职工人数是女职工人数的 ,女职工人数是全厂职工人数的几分之几?(
)
A. B. C.
【考点】分数除法应用题.
【分析】纺织厂男职工人数是女职工人数的 ,是把女职工的人数看成单位“1”,男职工
的人数是 ,那么总人数就是女职工的(1+ ),再用女职工的人数1除以总人数,即可
求出女职工人数是全厂职工人数的几分之几.
【解答】解:1÷(1+ )
=1÷
教育 11http://t.cn/Ri466E4
=
答:女职工人数是全厂职工人数的 .
故选:C.
19.三个连续的偶数中,最小的一个是a,最大的一个是几?( )
A.a+2 B.a+4 C.3a
【考点】奇数与偶数的初步认识;用字母表示数.
【分析】本题是一个用字母表示数的题,由所给条件可知a是三个连续偶数中最小一个数,
根据连续偶数的意义和性质得:a后面的两个数可用字母表示为:a+2,a+2+2表示.
【解答】解:由所给条件可知a是三个连续偶数中最小一个数,根据连续偶数的意义和性
质得:a后面的两个数可用字母表示为:a+2,a+2+2表示;则这三个连续偶数是:a、
a+2、a+4,
三个偶数中最大为a+4.
故选:B.
20.用一根长100厘米的绳子围一个长方形,使长与宽的比是7:3.这个长方形的宽是(
)
A.35厘米 B.30厘米 C.15厘米
【考点】按比例分配应用题.
【分析】用长100厘米的绳子围成一个长方形,因为长方形的周长=(长+宽)×2,所以这
个长方形长与宽的和为100÷2=50(厘米),然后用按比例分配的方法列出算式解答即可.
【解答】解:100÷2× ,
=50× ,
=15(厘米);
答:这个长方形的宽是15厘米.
故选:C.
21.一杯盐水,水与盐的比是10:1.这杯盐水的含盐率大约是( )
A.9.09% B.10% C.11%
【考点】百分率应用题.
【分析】首先理解含盐率和盐水的概念,含盐率是指盐的质量占盐水质量的百分比,盐水
的质量等于盐的质量加上水的质量,由此列式为: ×100%,计算即可.
【解答】解: ×100%,
= ×100%,
≈9.09%;
答:这杯盐水的含盐率大约是9.09%.
故选:A.
教育 12http://t.cn/Ri466E4
四、按照要求画图.9分
22.下面是一个长方体的正面、左面和下面的展开图.画出展开图的另外三个面,并标出
每个面是长方体的什么面.
【考点】长方体的展开图.
【分析】根据长方体的面的特征,长方体的6个面都是长方形(特殊情况有两个相对的面
是正方形),相对的面的面积相等.由此解答.
【解答】解:根据分析,作图如下:
23.五年级一班的女生人数占全班人数的 .在下面的线段图上标出表示这个班女生人数
和男生人数的部分.
【考点】分数的意义、读写及分类.
【分析】五年级一班的女生人数占全班人数的 ,则男生占 ,也就是说女生占5份,男
生占4份,用线段图表示出来即可.
【解答】解:五年级一班的女生人数占全班人数的 ,也就是说女生占5份,男生占4份,
用线段图表示为:
教育 13http://t.cn/Ri466E4
24.一个直角三角形两条直角边的长度比是3:2,其中较长的一条直角边是6厘米,算出
另一条直角边的长度,画出这个直角三角形.
【考点】画指定面积的长方形、正方形、三角形;比的应用.
【分析】由题意可知:把较长的一条直角边看作3份的量,于是可以求出1份的量,从而
可以求出另一条直角边的长度;两条直角边的长度已知,就能作出符合要求的三角形.
【解答】解:直角三角形的另一条直角边:6÷3×2=4(厘米);
于是作图如下:
.
五、解决实际问题.33分
25.根据题意列方程.(只要求写出设句,列出方程.)
1)赵欣买3.5千克苹果和5千克梨,一共用去60.5元.如果每千克苹果的单价是8元,每
千克梨多少元?
2)王师傅和张师傅共同加工一批零件.如果王师傅每天加工8个,张师傅每天加工6个,
多少天后王师傅比张师傅多加工14个?
【考点】列方程解应用题(两步需要逆思考).
【分析】(1)这道题的等量关系非常明显,3.5千克苹果的总价+5千克梨的总价=60.5元,
设每千克梨x元,列方程解答即可.
(2)设x天后王师傅比张师傅多加工14个,其数量关系是:王师傅x天加工的数量﹣张
师傅x天加工的数量=14个,由此列方程解答即可.
【解答】解:(1)设每千克梨x元,
3.5×8+5x=60.5
28+5x=60.5;
(2)设x天后王师傅比张师傅多加工14个,
8x﹣6x=14
2x=14;
故答案为:(1)28+5x=60.5,(2)2x=14.
教育 14http://t.cn/Ri466E4
26.一台拖拉机昨天上午耕地4800平方米,下午耕地的面积是上午的 .这台拖拉机昨天
一共耕地多少平方米?
【考点】分数四则复合应用题.
【分析】下午耕地的面积是上午的 ,已知上午耕地4800平方米,所以下午耕地:4800×
=3840平方米,则昨天全天耕地:4800+3840=8640平方米.
【解答】解:4800+4800× ,
=4800+3840,
=8640(平方米).
答:这台拖拉机昨天一天共耕地8640平方米.
27.李林有120张邮票,相当于陆红的 .陆红有多少张邮票?
【考点】分数除法应用题.
【分析】把陆红的邮票张数看成单位“1”,它的 对应的数量是120张,求陆红的邮票的
张数用除法.
【解答】解:120 =160(张);
答:陆红有160张邮票.
28.东林小学一共有学生1600人.六年级有200人,其中女生98人.六年级学生占全校
学生数的百分之几?六年级男生人数占全年级学生数的百分之几?
【考点】百分数的实际应用.
【分析】要求六年级学生数占全校学生数的百分之几,用“六年级学生人数÷学校总人
数”,要求六年级男生人数占全年级学生数的百分之几,先用六年级的总人数减去女生人
数求出男生的人数,再用“六年级男生人数÷全年级总人数”解答即可.
【解答】解:200÷1600=12.5%;
(200-98)÷200
=102÷200
=51%
答:六年级学生占全校学生数的12.5%,六年级男生人数占全年级学生数的51%.
29.一个长方体沙坑的长6米,宽4米,深0.8米.挖这个沙坑一共要挖出多少立方米的泥
土?如果要在沙坑的四周抹水泥,抹水泥的面积是多少平方米?
【考点】长方体、正方体表面积与体积计算的应用.
【分析】求挖这个沙坑一共要挖出多少立方米的泥土,实际上是求长、宽、高分别为6米、
4米和0.8米的长方体的体积,代入长方体的体积公式即可求解;
求抹水泥的面积,就是求沙坑四周四个面的面积,将数据代入长方形面积公式即可求解.
【解答】解:挖出的沙的体积:6×4×0.8,
=24×0.8,
教育 15http://t.cn/Ri466E4
=19.2(立方米);
抹水泥的面积:6×0.8×2+4×0.8×2,
=9.6+6.4,
=16(平方米);
答:挖这个沙坑一共要挖出19.2立方米的泥土,抹水泥的面积16平方米.
30.王老师买了8个网球和1个足球,正好用去360元.足球的单价是网球的4倍,足球
和网球的单价各是多少元?
【考点】和倍问题.
【分析】根据题干买了8个网球和1个足球,正好用去360元,那么可以设网球的单价是x
元,则足球的单价就是4x元,由此即可列出方程解决问题
【解答】解:设网球的单价是x元,则足球的单价就是4x,根据题意可得方程:
8x+4x=360,
12x=360,
x=30,
30×4=120(元);
答:足球120元,网球30元.
教育 16http://t.cn/Ri466E4
2016年8月17日
教育 17