文档内容
http://t.cn/Ri466E4
江苏省泰州市姜堰市克强学校六年级(上)期中数学试卷
一、看清算式细心计算
1.直接写得数
1
0
× ×× ×
÷ ×
1
2 2
4
= =
= = = =
4
×
1
×
﹣
÷÷4 ÷
+ ×
=
= = =
= =
2.计算下面各题.
÷ ×2
× ×
﹣ ×
÷ × .
3.解方程.
3x+4=5.5
4x÷ =
x﹣5=16.
二、填空.(22分,每空1分)
4.
公
倾
时
=
=
平
分
方
米
4 1
0 5
0 4
毫0
教育 1http://t.cn/Ri466E4
千
升克
= =
升吨
.
5. 吨的 是15吨,18米的 是 米, 平方米是 平方米的
.
6.一个长方体纸箱,长5分米,宽3分米,高4分米,它所有的棱长的和是
分米,占地面积是 平方分米,做这样一个纸箱需要纸板 平方分
米,它的体积是 立方分米.
7.某个车间去年生产50万个零件,今年比去年增产 ,今年比去年多生产
万个零件,今年生产零件 万个.
8.看图写算式: ○ = .
9. : 的比值是 ,把4:0.8化成最简整数比是 :
.
10.一个长方体的长是20厘米、宽是10厘米,高是8厘米,从这块木头上切下一个最大
的正方体后,剩下部分的体积是 立方厘米.
11.食堂有煤 吨,如果每天烧这堆煤的 ,一共可以烧 天;如果每天烧
吨,一共可以烧 天.
12.元旦期间同学们布置教室,一根彩带长20米,第一次用去它的 ,第二次又用去 米,
还剩 米.
13.根据条件,把数量关系式补充完整.
(1)女生人数是男生的 . 的人数× = 的人数
(2)苹果比梨多 . 的个数× = 的个数.
三.判断.(5分,每题1分)
14.两个长方体体积相等,底面积一定相等. .(判断对错)
15.两个数只要乘积是1,就一定互为倒数. .
16.五个小正方体叠成一排,体积和表面积都是不变. .
17.A和B都是非零的自然数,如果 ,则A>B. .
18.甲绳长6米,乙绳比甲绳长 米,乙绳长8米. . (判断对错)
教育 2http://t.cn/Ri466E4
四.选择.(5分,每题1分)
19.修路队修一条路,第一天修了全长的 ,还剩 米,第一天修的与剩下的( )
A.一样长 B.第一天的长 C.剩下的长 D.无法确定
20.一台榨油机 小时榨油 吨,1小时可榨油 吨,榨油1吨需要
小时.
A. ÷ B. ÷ C. × D. × .
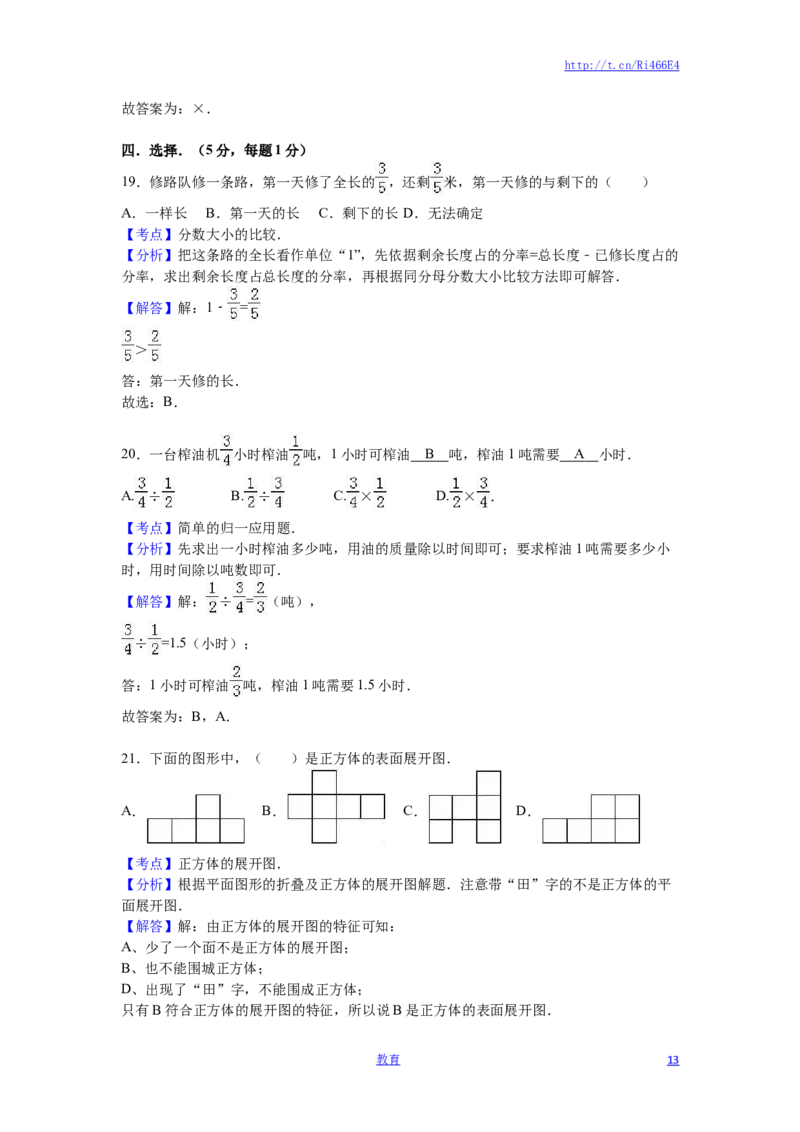
21.下面的图形中,( )是正方体的表面展开图.
A. B. C. D.
22.把长7厘米,宽5厘米,厚3厘米的长方体肥皂两块包装在一起,用( )平方厘
米包装纸最节省.
A.127 B.242 C.214 D.254
23.m是非0的自然数,下列算式中得数最大的是( )
A.m﹣ B.m÷ C.m× D.m+
五、明确要求动手操作
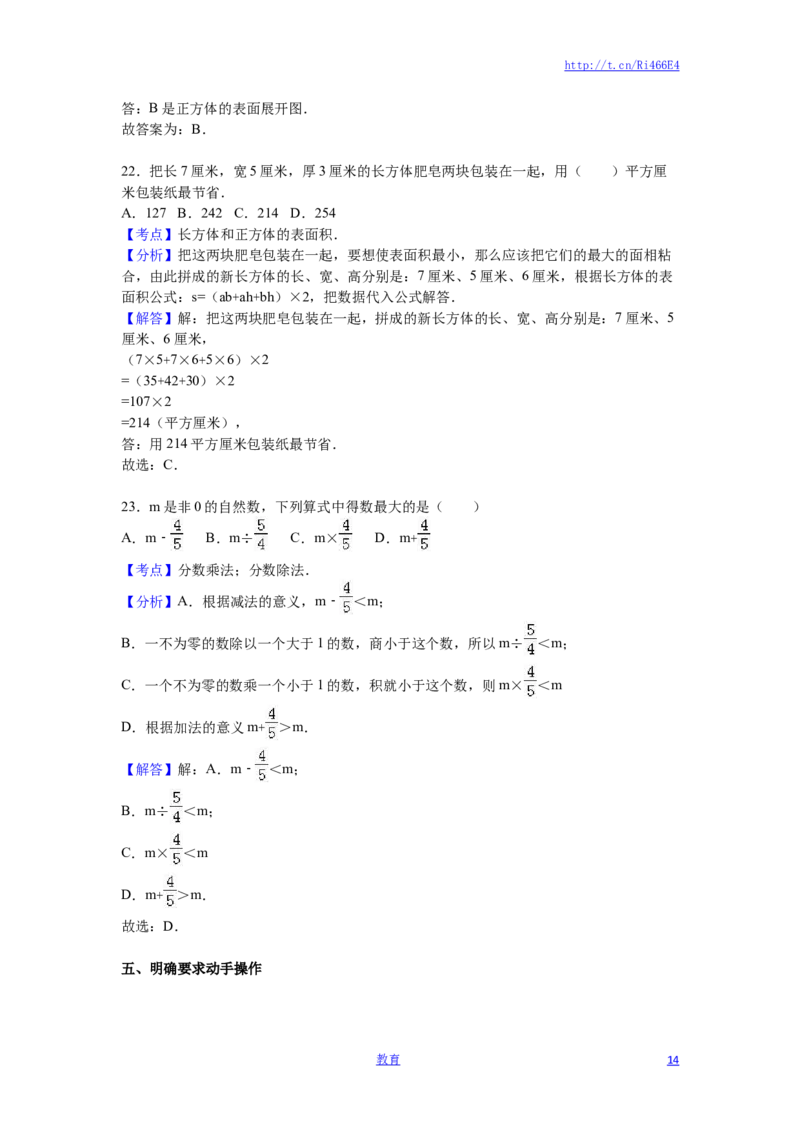
24.先在长方形中涂色表示它的 ,再画斜线表示 与 的乘积,最后完成下面的填空.
× =
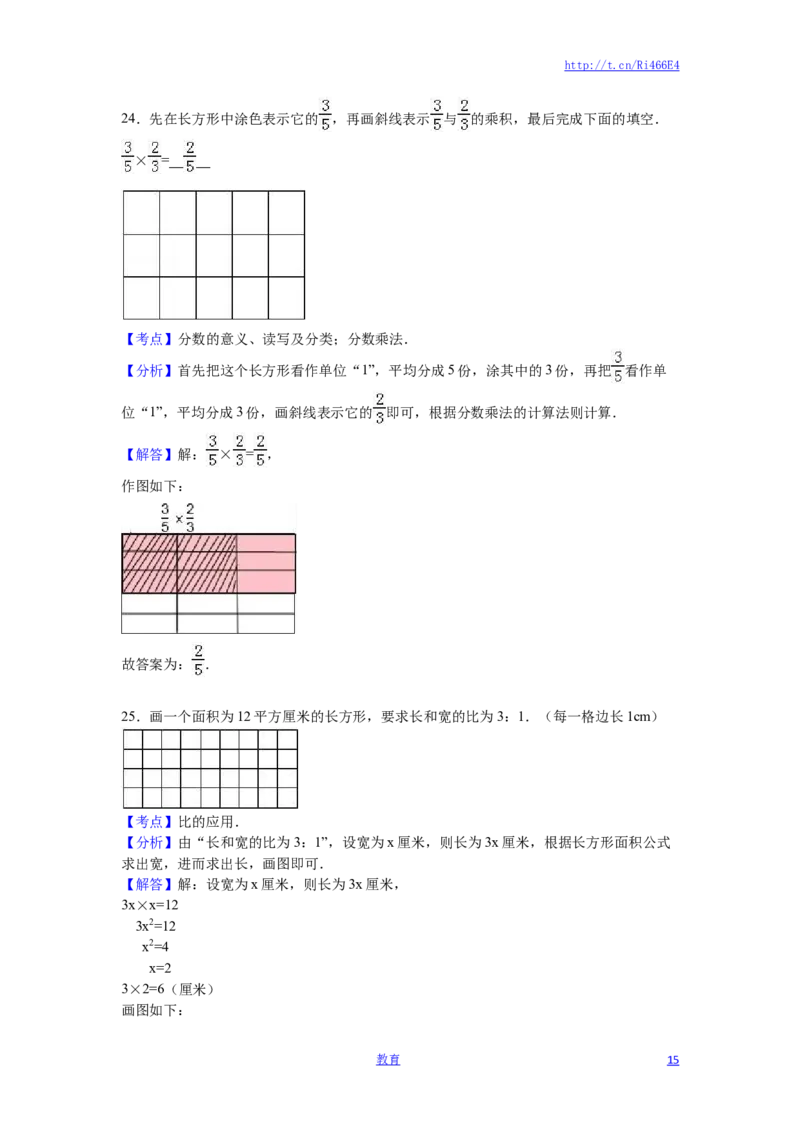
25.画一个面积为12平方厘米的长方形,要求长和宽的比为3:1.(每一格边长1cm)
六、联系实际,解决问题
26.某厂九月份用水28吨,十月份比九月份节约 ,十月份比九月份节约多少吨?
教育 3http://t.cn/Ri466E4
27.阳光书城购进故事书700本,相当于科技书的 .故事书比科技书少多少本?
28.一根电线长56米,第一次用去 ,第二次用去 米,现在比原来短了多少米?
29.配制一种混凝土所需的水泥、黄沙和石子的比是2:3:5,现在要配制80吨这样的混
凝土,需要石子多少吨?如果黄沙和水泥各有24吨,当黄沙全部用完时,水泥还剩多少吨?
30.一种车载铁皮油箱,长0.8米,宽0.6米,高0.5米.
(1)做这个油箱至少需要多少平方米的铁皮?
(2)如果每升油重0.75千克,这个油箱可装油多少千克?
31.压路机压一条长 千米的水渠,3台压路机 小时压完,平均每台压路机每小时挖多少
千米?
教育 4http://t.cn/Ri466E4
江苏省泰州市姜堰市克强学校六年级(上)期中数学试
卷
参考答案与试题解析
一、看清算式细心计算
1.直接写得数
×
÷2= ×14= 10× = ×2= × =
=
÷ ÷ ×4+ 1﹣ ÷ 4× ×
= = = = = =
【考点】分数乘法;分数除法.
【分析】根据分数加减乘除的运算方法口算即可,注意检查,注意计算 ×4+ 时,应用
乘法分配律.
【解答】解:
× = × =
÷2= ×14=4 10× =8 ×2=
÷ = ÷ = 1﹣ = ÷ =
×4+ =
4× × =
2
2.计算下面各题.
÷ ×2
× ×
﹣ ×
÷ × .
【考点】分数的四则混合运算.
【分析】(1)、(2)、(4)按照从左向右的顺序进行计算;
(3)先算乘法,再算减法.
【解答】解:(1) ÷ ×2
= ×2
教育 5http://t.cn/Ri466E4
= ;
(2) × ×
= ×
= ;
(3) ﹣ ×
= ﹣1
= ;
(4) ÷ ×
= ×
= .
3.解方程.
3x+4=5.5
4x÷ =
x﹣5=16.
【考点】方程的解和解方程.
【分析】(1)根据等式的性质,在方程两边同时减去4再同除以3求解;
(2)根据等式的性质,在方程两边同时乘上 再同除以4求解;
(3)根据等式的性质,在方程两边同时加上5再同乘上 求解.
【解答】解:(1)3x+4=5.5
3x+4﹣4=5.5﹣4
3x=1.5
3x÷3=1.5÷3
x=0.5;
(2)4x÷ =
教育 6http://t.cn/Ri466E4
4x÷ × = ×
4x=
4x÷4= ÷4
x= ;
(3) x﹣5=16
x﹣5+5=16+5
x=21
x× =21×
x=28.
二、填空.(22分,每空1分)
4.
时= 4 5 分 公倾= 600 0 平方米
400毫升= 0. 4 升 1540千克= 1.5 4 吨.
【考点】时、分、秒及其关系、单位换算与计算;质量的单位换算;面积单位间的进率及
单位换算;体积、容积进率及单位换算.
【分析】把 时换算为分钟,用 乘进率60;
把 公顷换算为平方米,用 乘进率10000;
把400毫升换算为升,用400除以进率1000;
把1540千克换算为吨,用1540除以进率1000.
【解答】
解: 时=45分 公倾=6000平方米
400毫升=0.4升 1540千克=1.54吨
故答案为:45,6000,0.4,1.54.
5. 2 0 吨的 是15吨,18米的 是 1 5 米, 平方米是 平方米的 .
【考点】分数除法;分数乘法.
【分析】(1)把所求的重量看作单位“1”,根据分数除法的意义,用15除以它占所求的
重量的分率,求出多少吨的 是15吨即可.
教育 7http://t.cn/Ri466E4
(2)把18米看作单位“1”,根据分数乘法的意义,用18乘以 ,求出18米的 是多少米
即可.
(3)把 平方米看作单位“1”,用 除以 ,求出 平方米是 平方米的几分之几即可.
【解答】解:(1)15÷ =20(吨)
答:20吨的 是15吨.
(2)18× =15(米)
答:18米的 是15米.
(3) ÷ =
答: 平方米是 平方米的 .
故答案为:20、15、 .
6.一个长方体纸箱,长5分米,宽3分米,高4分米,它所有的棱长的和是 4 8 分米,
占地面积是 1 5 平方分米,做这样一个纸箱需要纸板 9 4 平方分米,它的体积是 6 0
立方分米.
【考点】长方体、正方体表面积与体积计算的应用.
【分析】我们运用(1)长宽高的和乘以4就是长方体纸箱棱长的和.(2)运用长乘以宽
就是底面积.(3)运用(长×宽+长×高+宽×高)×2就是做这样一个纸箱需要纸板的面
积.(4)运用“长×宽×高=体积”进行计算即可.
【解答】解:(1)(5+3+4)×4,
=12×4,
=48(分米);
答:它所有的棱长的和是48分米.
(2)5×3=15(平方分米);
答:占地面积是15平方分米.
(3)(5×3+5×4+3×4)×2,
=(15+20+12)×2,
=94(平方分米);
(4)5×3×4,
=15×4,
=60(立方分米);
答:它的体积是60立方分米.
教育 8http://t.cn/Ri466E4
7.某个车间去年生产50万个零件,今年比去年增产 ,今年比去年多生产 5 万个零
件,今年生产零件 5 5 万个.
【考点】分数四则复合应用题.
【分析】已知去年生产50万个零件,今年比去年增产 ,要求今年比去年多生产多少万
个零件,把50万个看作单位“1”,也就是增产了50万个的 ,列式为50× ,计算即
可;
要求今年生产零件多少万个,用去年生产的零件个数加上今年比去年多生产的零件个数即
可.
【解答】解:(1)50× =5(万个);
(2)50+5=55(万个);
答:今年比去年多生产5万个零件,今年生产零件55万个.
故答案为:5,55.
8.看图写算式: ○ = .
【考点】分数乘法.
【分析】根据图,可以看作成一张纸,把这张纸平均分成了12份,取了其中的8份,也就
是 ,;又把 张纸平均分成8份,取了其中的6份,也就是取了 张纸的 ,即
× ,然后再进行计算即可.
【解答】解:根据题意可得:
× = .
故答案为: , , .
9. : 的比值是 ,把4:0.8化成最简整数比是 5 : 1 .
【考点】求比值和化简比.
【分析】(1)用比的前项除以后项,即可求出比值;
(2)根据比的基本性质解答,即把比的前项和后项同乘一个数或除以一个数(0除外)比
值不变.
【解答】解:(1) : ,
教育 9http://t.cn/Ri466E4
= ÷ ,
= ×3,
= ;
(2)4:0.8=(4×10):(0.8×10),
=40:8,
=(40÷8):(8÷8),
=5:1;
故答案为: ,5:1.
10.一个长方体的长是20厘米、宽是10厘米,高是8厘米,从这块木头上切下一个最大
的正方体后,剩下部分的体积是 108 8 立方厘米.
【考点】长方体和正方体的体积;正方体的特征.
【分析】先求出原来长方体的体积,再求出切下的最大正方体的体积,最大正方体应以高
为棱长(因为高最短),再求出得数.
【解答】解:长方体的体积:20×10×8=1600(立方厘米),
最大正方体的体积:8×8×8=512(立方厘米),
剩下部分的体积:1600﹣512=1088(立方厘米);
答:剩下部分的体积是1088立方厘米.
故答案为:1088.
11.食堂有煤 吨,如果每天烧这堆煤的 ,一共可以烧 8 天;如果每天烧 吨,一共
可以烧 3 天.
【考点】分数除法应用题.
【分析】把煤的总重量看作单位“1”,如果每天烧这堆煤的 ,求一共可以烧多少天,用
1除以 即可;
求如果每天烧 吨,一共可以烧多少天,用 除以 即可.
【解答】解:1÷ =8(天)
÷ =3(天)
答:如果每天烧这堆煤的 ,一共可以烧 8天;如果每天烧 吨,一共可以烧 3天.
故答案为:8,3.
教育 10http://t.cn/Ri466E4
12.元旦期间同学们布置教室,一根彩带长20米,第一次用去它的 ,第二次又用去 米,
还剩 9 米.
【考点】分数四则复合应用题.
【分析】第一次用去20米的 ,第二次用去 米,从20米里减去两次用的米数就是剩下
的米数.
【解答】解:20﹣20× ﹣ ,
=20﹣10﹣ ,
=9 (米);
答:还剩9 米.
故答案为:9 .
13.根据条件,把数量关系式补充完整.
(1)女生人数是男生的 . 男生 的人数× = 女生 的人数
(2)苹果比梨多 . 梨 的个数× = 苹果比梨多 的个数.
【考点】分数乘法应用题.
【分析】(1)把男生人数看作单位“1”,则女生人数的分率为男生人数的 ,则男生人数
× =女生的人数;
(2)把梨的个数看作单位“1”,则苹果比梨多 ,即:梨的个数× =苹果比梨多的个数.
【解答】解:(1)女生人数是男生的 . 男生的人数× =女生的人数;
(2)苹果比梨多 . 梨的个数× =苹果比梨多的个数.
故答案为:男生,女生;梨,苹果比梨多.
三.判断.(5分,每题1分)
14.两个长方体体积相等,底面积一定相等. 错误 .(判断对错)
【考点】长方体和正方体的体积.
【分析】根据长方体的体积计算方法可知,长方体的体积是由它的底面积和高两个条件决
定的,两个长方体的体积相等,如果它们的高不相等,那么它们的底面积也就不相等,由
此判断即可.
【解答】解:由于长方体的体积是由它的底面积和高两个条件决定的,
教育 11http://t.cn/Ri466E4
所以两个长方体体积相等,底面积不一定相等;
所以原题说法是错误的.
故答案为:错误.
15.两个数只要乘积是1,就一定互为倒数. √ .
【考点】倒数的认识.
【分析】根据倒数的意义:乘积是1的两个数互为倒数.判断两个数是不是互为倒数,就
是看这个数数的乘积是不是1.据此解答.
【解答】解:根据倒数的意义,两个数只要乘积是1,就一定互为倒数.此说法正确.
故答案为:√.
16.五个小正方体叠成一排,体积和表面积都是不变. × .
【考点】简单的立方体切拼问题.
【分析】把五个一样的正方体叠成一排拼成一个长方体后,所占的空间没变,所以体积不
变,但是表面积变了,减少了相叠连的8个面的面积.
【解答】解:把五个一样的正方体叠成一排拼成一个长方体后,体积不变但是表面积变了.
故判断为:×.
17.A和B都是非零的自然数,如果 ,则A>B. √ .
【考点】分数大小的比较;比例的意义和基本性质.
【分析】先令 =1,分别求出A、B的值,在比较其大小即可.
【解答】解:令 =1,
则令A× =1,A=8,
B× =1,B=7,
又因8>7,
所以A>B,
故答案为:√.
18.甲绳长6米,乙绳比甲绳长 米,乙绳长8米. × . (判断对错)
【考点】分数的加法和减法.
【分析】根据加法的意义,用6米加上 米解答即可.
【解答】解:6+ =6 (米);
答:乙绳长6 米.
所以甲绳长6米,乙绳比甲绳长 米,乙绳长8米. 说法错误;
教育 12http://t.cn/Ri466E4
故答案为:×.
四.选择.(5分,每题1分)
19.修路队修一条路,第一天修了全长的 ,还剩 米,第一天修的与剩下的( )
A.一样长 B.第一天的长 C.剩下的长 D.无法确定
【考点】分数大小的比较.
【分析】把这条路的全长看作单位“1”,先依据剩余长度占的分率=总长度﹣已修长度占的
分率,求出剩余长度占总长度的分率,再根据同分母分数大小比较方法即可解答.
【解答】解:1﹣ =
>
答:第一天修的长.
故选:B.
20.一台榨油机 小时榨油 吨,1小时可榨油 B 吨,榨油1吨需要 A 小时.
A. ÷ B. ÷ C. × D. × .
【考点】简单的归一应用题.
【分析】先求出一小时榨油多少吨,用油的质量除以时间即可;要求榨油1吨需要多少小
时,用时间除以吨数即可.
【解答】解: ÷ = (吨),
÷ =1.5(小时);
答:1小时可榨油 吨,榨油1吨需要1.5小时.
故答案为:B,A.
21.下面的图形中,( )是正方体的表面展开图.
A. B. C. D.
【考点】正方体的展开图.
【分析】根据平面图形的折叠及正方体的展开图解题.注意带“田”字的不是正方体的平
面展开图.
【解答】解:由正方体的展开图的特征可知:
A、少了一个面不是正方体的展开图;
B、也不能围城正方体;
D、出现了“田”字,不能围成正方体;
只有B符合正方体的展开图的特征,所以说B是正方体的表面展开图.
教育 13http://t.cn/Ri466E4
答:B是正方体的表面展开图.
故答案为:B.
22.把长7厘米,宽5厘米,厚3厘米的长方体肥皂两块包装在一起,用( )平方厘
米包装纸最节省.
A.127 B.242 C.214 D.254
【考点】长方体和正方体的表面积.
【分析】把这两块肥皂包装在一起,要想使表面积最小,那么应该把它们的最大的面相粘
合,由此拼成的新长方体的长、宽、高分别是:7厘米、5厘米、6厘米,根据长方体的表
面积公式:s=(ab+ah+bh)×2,把数据代入公式解答.
【解答】解:把这两块肥皂包装在一起,拼成的新长方体的长、宽、高分别是:7厘米、5
厘米、6厘米,
(7×5+7×6+5×6)×2
=(35+42+30)×2
=107×2
=214(平方厘米),
答:用214平方厘米包装纸最节省.
故选:C.
23.m是非0的自然数,下列算式中得数最大的是( )
A.m﹣ B.m÷ C.m× D.m+
【考点】分数乘法;分数除法.
【分析】A.根据减法的意义,m﹣ <m;
B.一不为零的数除以一个大于1的数,商小于这个数,所以m÷ <m;
C.一个不为零的数乘一个小于1的数,积就小于这个数,则m× <m
D.根据加法的意义m+ >m.
【解答】解:A.m﹣ <m;
B.m÷ <m;
C.m× <m
D.m+ >m.
故选:D.
五、明确要求动手操作
教育 14http://t.cn/Ri466E4
24.先在长方形中涂色表示它的 ,再画斜线表示 与 的乘积,最后完成下面的填空.
× =
【考点】分数的意义、读写及分类;分数乘法.
【分析】首先把这个长方形看作单位“1”,平均分成5份,涂其中的3份,再把 看作单
位“1”,平均分成3份,画斜线表示它的 即可,根据分数乘法的计算法则计算.
【解答】解: × = ,
作图如下:
故答案为: .
25.画一个面积为12平方厘米的长方形,要求长和宽的比为3:1.(每一格边长1cm)
【考点】比的应用.
【分析】由“长和宽的比为3:1”,设宽为x厘米,则长为3x厘米,根据长方形面积公式
求出宽,进而求出长,画图即可.
【解答】解:设宽为x厘米,则长为3x厘米,
3x×x=12
3x2=12
x2=4
x=2
3×2=6(厘米)
画图如下:
教育 15http://t.cn/Ri466E4
六、联系实际,解决问题
26.某厂九月份用水28吨,十月份比九月份节约 ,十月份比九月份节约多少吨?
【考点】分数乘法应用题.
【分析】根据“十月份比九月份节约 ”,是把九月份用水28吨看作单位“1”,求十月份
比九月份节约的吨数,就是求28的 是多少,根据分数乘法的意义,列式为28× .
【解答】解;十月份比九月份节约的吨数:
28× =4(吨).
答:十月份比九月份节约4吨.
27.阳光书城购进故事书700本,相当于科技书的 .故事书比科技书少多少本?
【考点】分数除法应用题.
【分析】把故事书的本数看作单位“1”(未知),根据已知一个数的几分之几是多少,求
这个数,用除法求出科技书的本数,然后减去科技书的本数即可.
【解答】解:700÷ ﹣700
=840﹣700
=140(本)
答:故事书比科技书少140本.
28.一根电线长56米,第一次用去 ,第二次用去 米,现在比原来短了多少米?
【考点】分数四则复合应用题.
【分析】一根电线长56米,第一次用去 ,根据分数乘法的意义,第一次用去了56× 米,
又第二次用去 米,所以两次共用了了56× + 米,用去的米数即得现在比原来短了多少
米.
【解答】解:56× +
=14+
=14 (米)
教育 16http://t.cn/Ri466E4
答:现在比原来短了14 米.
29.配制一种混凝土所需的水泥、黄沙和石子的比是2:3:5,现在要配制80吨这样的混
凝土,需要石子多少吨?如果黄沙和水泥各有24吨,当黄沙全部用完时,水泥还剩多少吨?
【考点】比的应用.
【分析】(1)混凝土水泥、黄沙、石子的配合比是2:3:5,先求出总份数,再求出石子
占总份数的几分之几,运用乘法的意义,即可求出需要石子多少吨;
(2)因为黄沙和水泥各有24吨,又因为黄沙24吨,配合比又是3,即毎份是24÷3=8
(吨).进一步解决问题.
【解答】解:(1)2+3+5=10,
80× =40(吨)
答:需要石子40吨.
(2)每份:24÷3=8(吨),
水泥剩下:24﹣8×2
=24﹣26
=8(吨)
答:水泥还剩8吨.
30.一种车载铁皮油箱,长0.8米,宽0.6米,高0.5米.
(1)做这个油箱至少需要多少平方米的铁皮?
(2)如果每升油重0.75千克,这个油箱可装油多少千克?
【考点】长方体、正方体表面积与体积计算的应用.
【分析】(1)运用(长×宽+长×高+宽×高)×2就是做这样一个油箱的面积.(2)运
用“长×宽×高=体积”进行计算求出体积,再把体积转化成容积单位,进一步求出重量.
【解答】解:(1)(0.8×0.6+0.8×0.5+0.6×0.5)×2,
=(0.48+0.4+0.3)×2,
=1.18×2,
=2.36(平方米);
答:做这个油箱至少需要2.36平方米的铁皮.
(2)0.8×0.6×0.5,
=0.8×(0.6×0.5),
=0.8×0.3,
=0.24(立方米);
0.24立方米=240立方分米,
240立方分米=240升,
0.75×240=180(千克);
答:这个油箱可装油180千克.
31.压路机压一条长 千米的水渠,3台压路机 小时压完,平均每台压路机每小时挖多少
千米?
教育 17http://t.cn/Ri466E4
【考点】分数除法应用题.
【分析】此题可先求3台压路机1小时挖的长度,再求平均每台压路机每小时挖的长度,
列式为 ÷ ÷3,解决问题.
【解答】解: ÷ ÷3
= ×
= (千米)
答:平均每台压路机每小时挖 千米.
教育 18http://t.cn/Ri466E4
2016年8月25日
教育 19