文档内容
2020年云南省中考数学试卷
一、填空题(本大题共6小题,每小题3分,共18分)
1.(3分)中国是最早采用正负数表示相反意义的量的国家.某仓库运进面粉 7吨,记为
+7吨,那么运出面粉8吨应记为 吨.
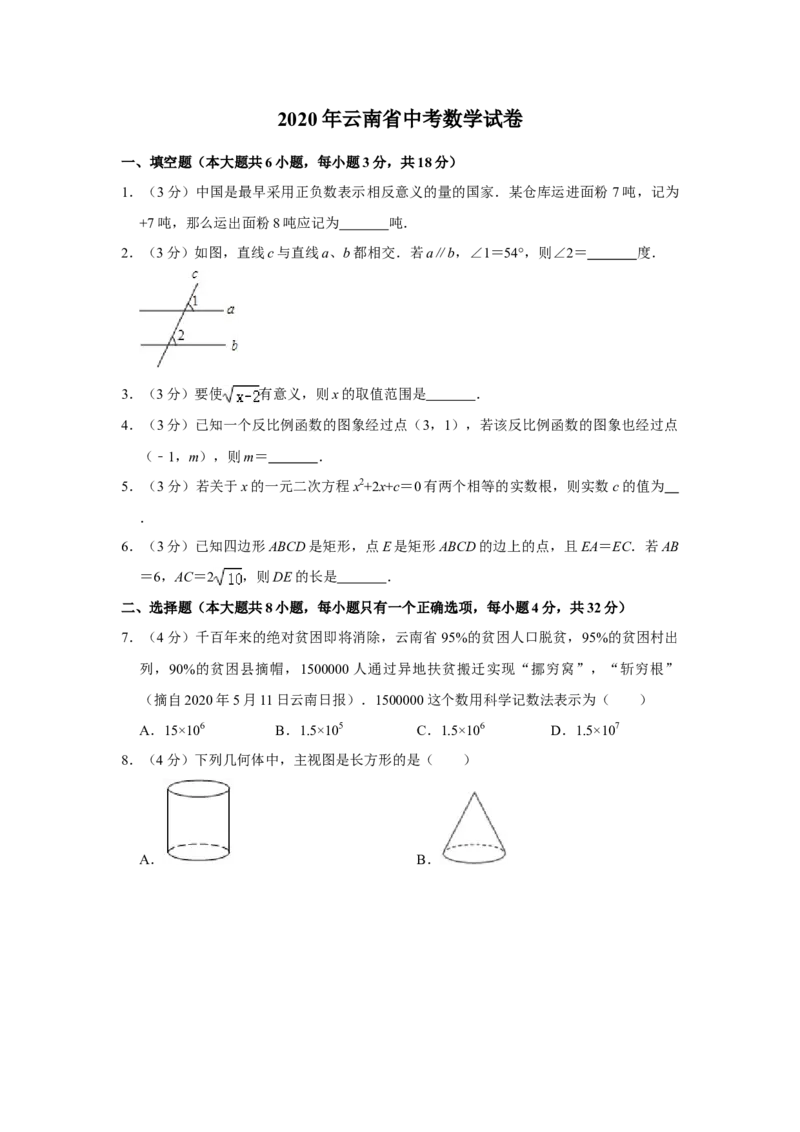
2.(3分)如图,直线c与直线a、b都相交.若a∥b,∠1=54°,则∠2= 度.
3.(3分)要使 有意义,则x的取值范围是 .
4.(3分)已知一个反比例函数的图象经过点(3,1),若该反比例函数的图象也经过点
(﹣1,m),则m= .
5.(3分)若关于x的一元二次方程x2+2x+c=0有两个相等的实数根,则实数c的值为
.
6.(3分)已知四边形ABCD是矩形,点E是矩形ABCD的边上的点,且EA=EC.若AB
=6,AC=2 ,则DE的长是 .
二、选择题(本大题共8小题,每小题只有一个正确选项,每小题4分,共32分)
7.(4分)千百年来的绝对贫困即将消除,云南省 95%的贫困人口脱贫,95%的贫困村出
列,90%的贫困县摘帽,1500000人通过异地扶贫搬迁实现“挪穷窝”,“斩穷根”
(摘自2020年5月11日云南日报).1500000这个数用科学记数法表示为( )
A.15×106 B.1.5×105 C.1.5×106 D.1.5×107
8.(4分)下列几何体中,主视图是长方形的是( )
A. B.C. D.
9.(4分)下列运算正确的是( )
A. =±2 B.( )﹣1=﹣2
C.(﹣3a)3=﹣9a3 D.a6÷a3=a3 (a≠0)
10.(4分)下列说法正确的是( )
A.为了解三名学生的视力情况,采用抽样调查
B.任意画一个三角形,其内角和是360°是必然事件
C.甲、乙两名射击运动员10次射击成绩(单位:环)的平均数分别为 、 ,方
差分别为s甲 2、s乙 2,若 = ,s甲 2=0.4,s乙 2=2,则甲的成绩比乙的稳定
D.一个抽奖活动中,中奖概率为 ,表示抽奖20次就有1次中奖
11.(4分)如图,平行四边形ABCD的对角线AC,BD相交于点O,E是CD的中点.则
△DEO与△BCD的面积的比等于( )
A. B. C. D.
12.(4分)按一定规律排列的单项式:a,﹣2a,4a,﹣8a,16a,﹣32a,…,第n个单
项式是( )
A.(﹣2)n﹣1a B.(﹣2)na C.2n﹣1a D.2na
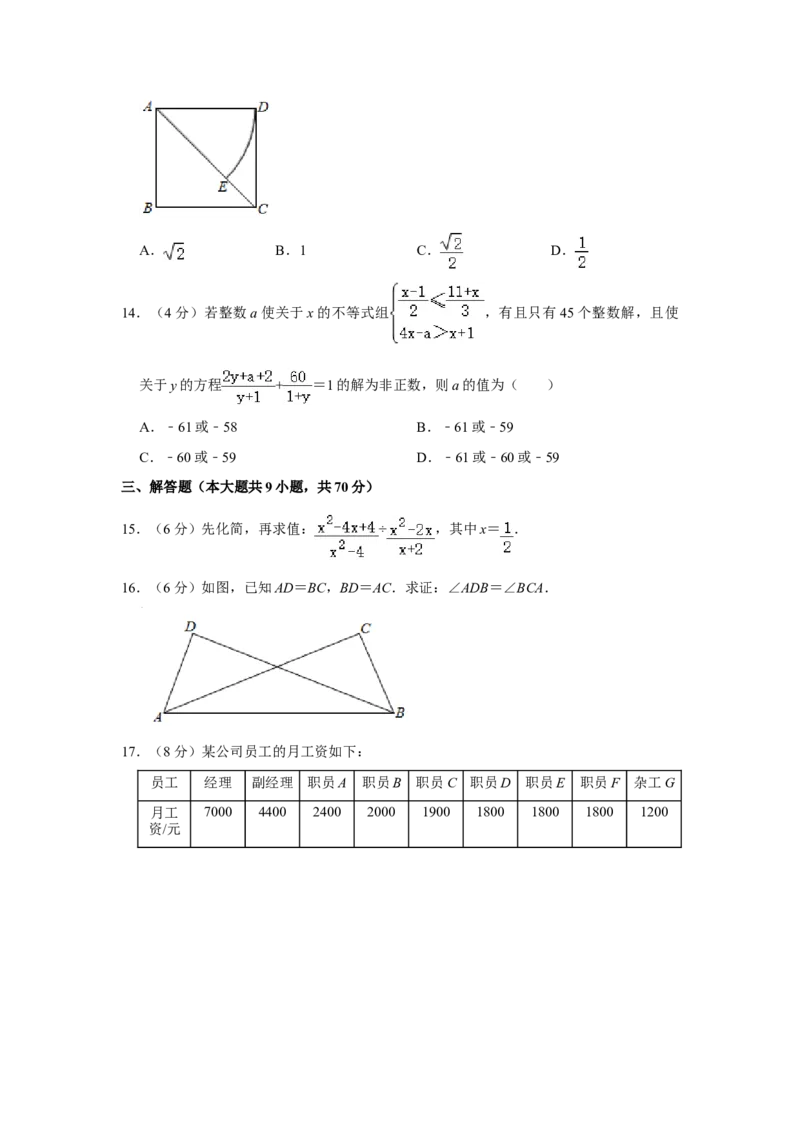
13.(4分)如图,正方形ABCD的边长为4,以点A为圆心,AD为半径,画圆弧DE得
到扇形DAE(阴影部分,点E在对角线AC上).若扇形DAE正好是一个圆锥的侧面展
开图,则该圆锥的底面圆的半径是( )A. B.1 C. D.
14.(4分)若整数a使关于x的不等式组 ,有且只有45个整数解,且使
关于y的方程 + =1的解为非正数,则a的值为( )
A.﹣61或﹣58 B.﹣61或﹣59
C.﹣60或﹣59 D.﹣61或﹣60或﹣59
三、解答题(本大题共9小题,共70分)
15.(6分)先化简,再求值: ÷ ,其中x= .
16.(6分)如图,已知AD=BC,BD=AC.求证:∠ADB=∠BCA.
17.(8分)某公司员工的月工资如下:
员工 经理 副经理 职员A 职员B 职员C 职员D 职员E 职员F 杂工G
月工 7000 4400 2400 2000 1900 1800 1800 1800 1200
资/元经理、职员C、职员D从不同的角度描述了该公司员工的收入情况.
设该公司员工的月工资数据(见上述表格)的平均数、中位数、众数分别为k、m、n,
请根据上述信息完成下列问题:
(1)k= ,m= ,n= ;
(2)上月一个员工辞职了,从本月开始,停发该员工工资,若本月该公司剩下的 8名
员工的月工资不变,但这8名员工的月工资数据(单位:元)的平均数比原9名员工的
月工资数据(见上述表格)的平均数减小了.你认为辞职的那名员工可能是 .
18.(6分)某地响应“把绿水青山变成金山银山,用绿色杠杆撬动经济转型”发展理念,
开展“美化绿色城市”活动,绿化升级改造了总面积为360万平方米的区域.实际施工
中,由于采用了新技术,实际平均每年绿化升级改造的面积是原计划平均每年绿化升级
改造的面积的2倍,所以比原计划提前4年完成了上述绿化升级改造任务.实际平均每
年绿化升级改造的面积是多少万平方米?
19.(7分)甲、乙两个家庭来到以“生态资源,绿色旅游”为产业的美丽云南,各自随
机选择到大理、丽江、西双版纳三个城市中的一个城市旅游.假设这两个家庭选择到哪
个城市旅游不受任何因素影响,上述三个城市中的每一个被选到的可能性相同,甲、乙
两个家庭选择到上述三个城市中的同一个城市旅游的概率为P.
(1)直接写出甲家庭选择到大理旅游的概率;
(2)用列表法或树状图法(树状图也称树形图)中的一种方法,求P的值.
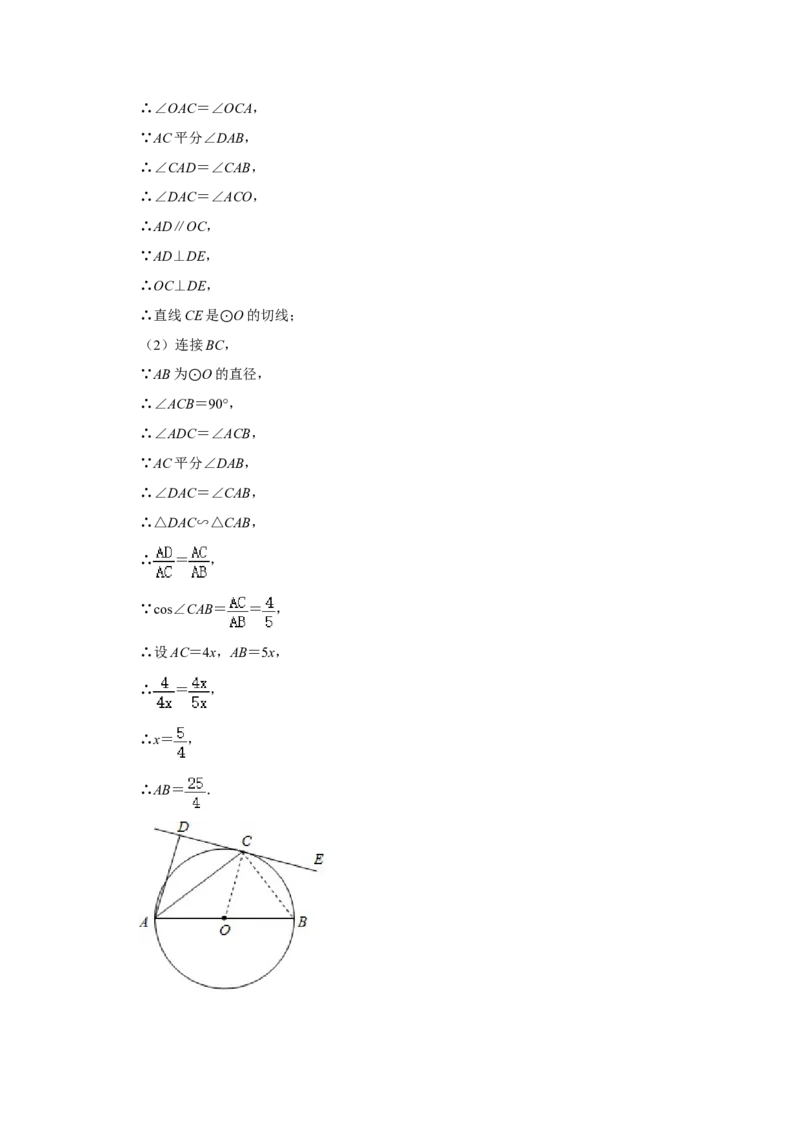
20.(8分)如图,AB为 O的直径,C为 O上一点,AD⊥CE,垂足为D,AC平分
⊙ ⊙∠DAB.
(1)求证:CE是 O的切线;
(2)若AD=4,co ⊙ s∠CAB= ,求AB的长.
21.(8分)众志成城抗疫情,全国人民在行动.某公司决定安排大、小货车共20辆,运
送260吨物资到A地和B地,支援当地抗击疫情.每辆大货车装15吨物资,每辆小货
车装10吨物资,这20辆货车恰好装完这批物资.已知这两种货车的运费如下表:
目的地 A地(元/辆) B地(元/辆)
车型
大货车 900 1000
小货车 500 700
现安排上述装好物资的20辆货车(每辆大货车装15吨物资,每辆小货车装10吨物资)
中的10辆前往A地,其余前往B地,设前往A地的大货车有x辆,这20辆货车的总运
费为y元.
(1)这20辆货车中,大货车、小货车各有多少辆?
(2)求y与x的函数解析式,并直接写出x的取值范围;
(3)若运往A地的物资不少于140吨,求总运费y的最小值.
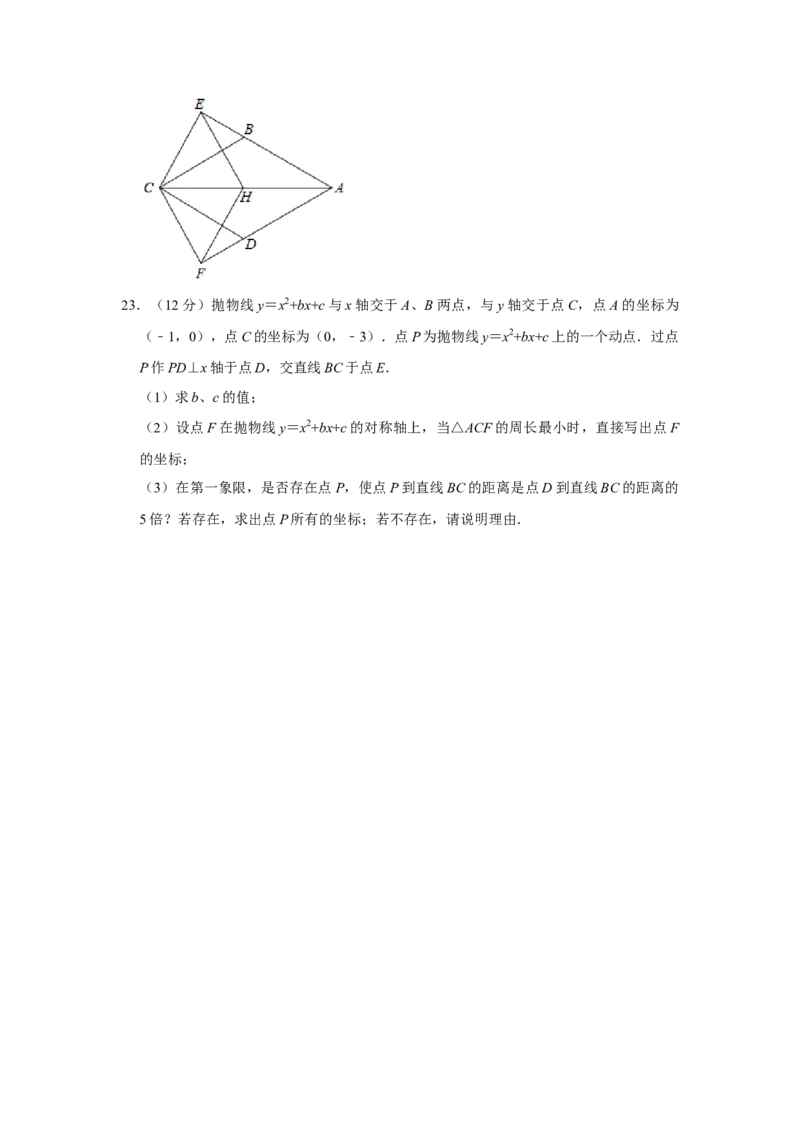
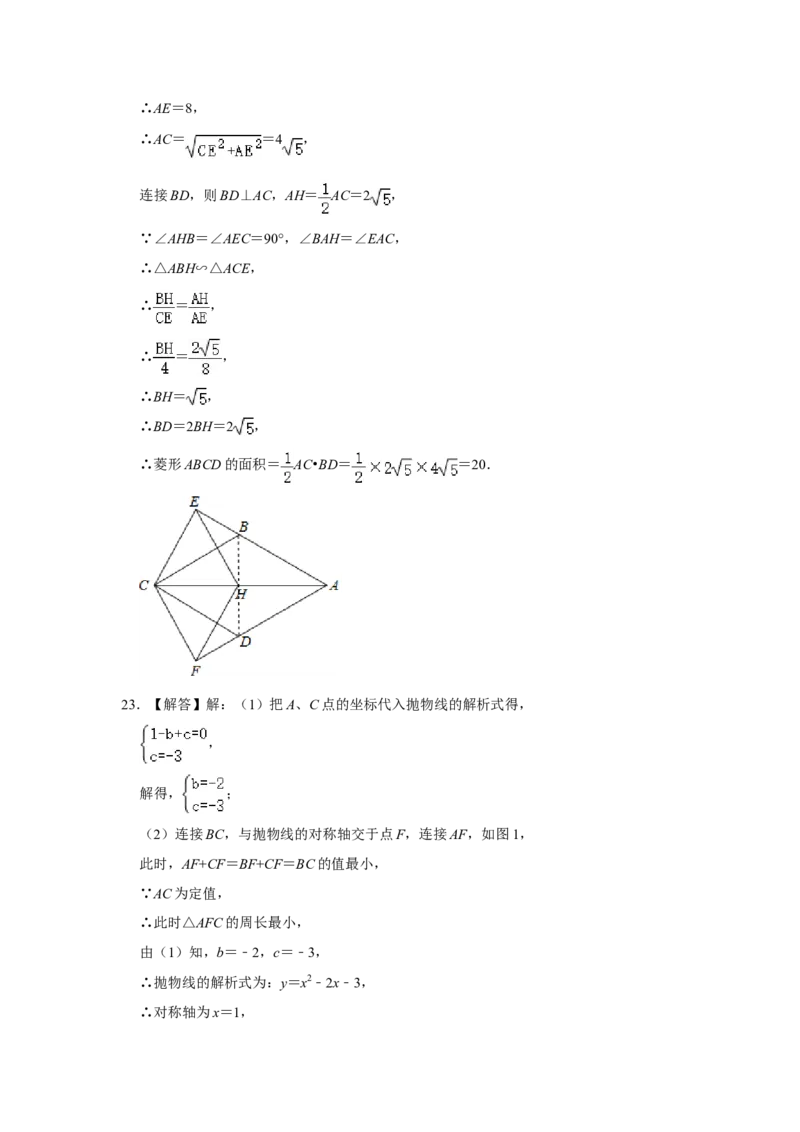
22.(9分)如图,四边形ABCD是菱形,点H为对角线AC的中点,点E在AB的延长线
上,CE⊥AB,重足为E,点F在AD的延长线上,CF⊥AD,重足为F,
(1)若∠BAD=60°,求证:四边形CEHF是菱形;
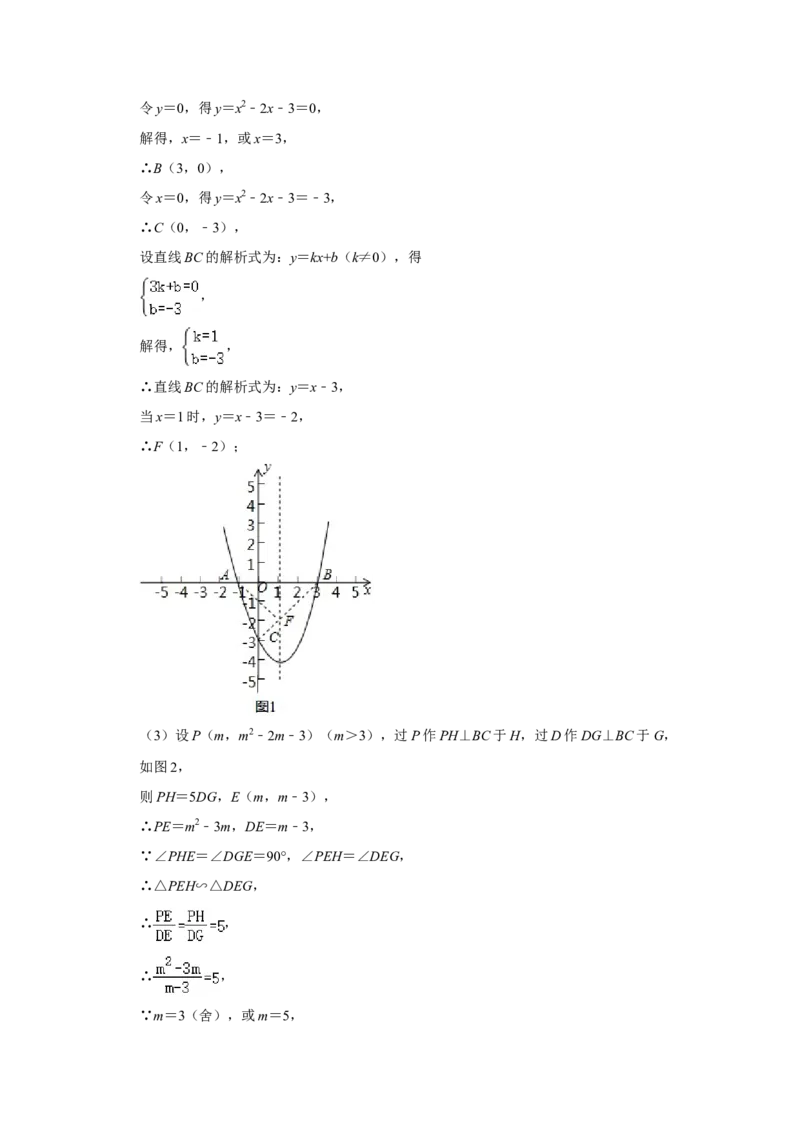
(2)若CE=4,△ACE的面积为16,求菱形ABCD的面积.23.(12分)抛物线y=x2+bx+c与x轴交于A、B两点,与y轴交于点C,点A的坐标为
(﹣1,0),点C的坐标为(0,﹣3).点P为抛物线y=x2+bx+c上的一个动点.过点
P作PD⊥x轴于点D,交直线BC于点E.
(1)求b、c的值;
(2)设点F在抛物线y=x2+bx+c的对称轴上,当△ACF的周长最小时,直接写出点F
的坐标;
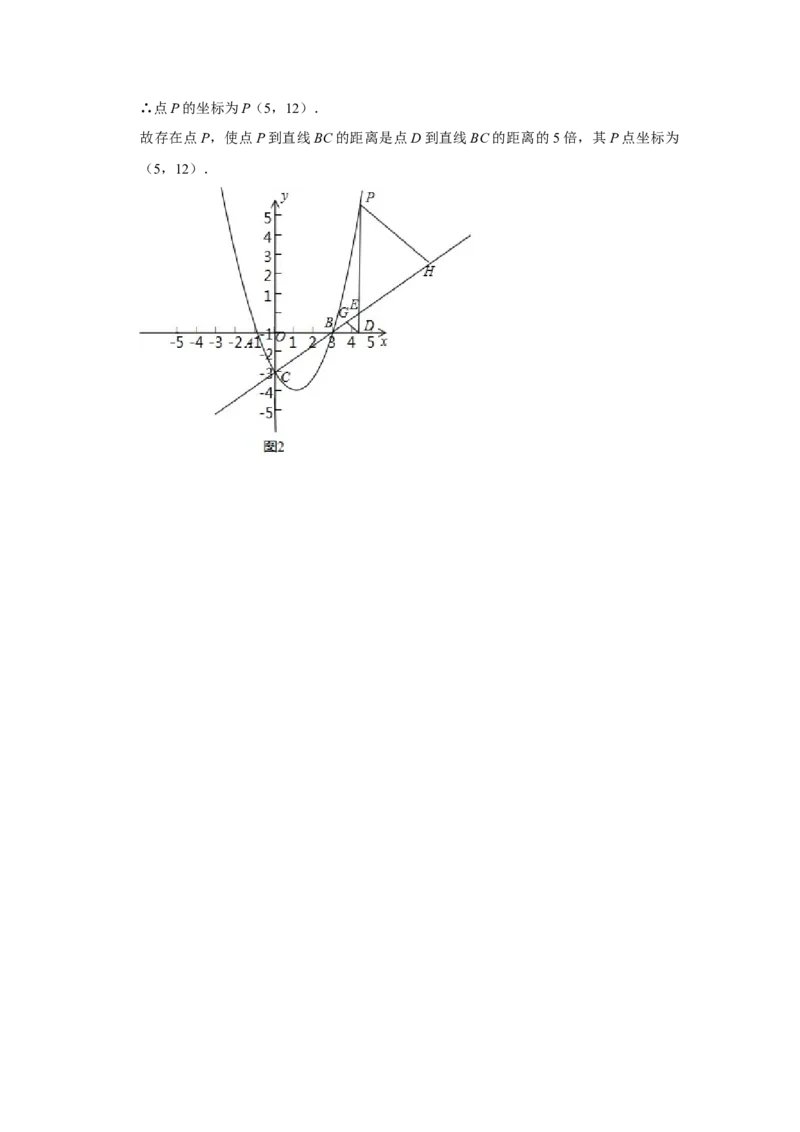
(3)在第一象限,是否存在点P,使点P到直线BC的距离是点D到直线BC的距离的
5倍?若存在,求出点P所有的坐标;若不存在,请说明理由.2020年云南省中考数学试卷
参考答案与试题解析
一、填空题(本大题共6小题,每小题3分,共18分)
1.【解答】解:因为题目运进记为正,那么运出记为负.
所以运出面粉8吨应记为﹣8吨.
故答案为:﹣8.
2.【解答】解:∵a∥b,∠1=54°,
∴∠2=∠1=54°.
故答案为:54.
3.【解答】解:∵ 有意义,
∴x﹣2≥0,
∴x≥2.
故答案为x≥2.
4.【解答】解:设反比例函数的表达式为y= ,
∵反比例函数的图象经过点(3,1)和(﹣1,m),
∴k=3×1=﹣m,
解得m=﹣3,
故答案为:﹣3.
5.【解答】解:∵关于x的一元二次方程x2+2x+c=0有两个相等的实数根,
∴△=b2﹣4ac=22﹣4c=0,
解得c=1.
故答案为1.
6.【解答】解:如图,
∵四边形ABCD是矩形,∴CD=AB=6,AD=BC,∠ABC=∠ADC=90°,
∴BC= = =2,
∴AD=2,
当点E在CD上时,
∵AE2=DE2+AD2=EC2,
∴(6﹣DE)2=DE2+4,
∴DE= ;
当点E在AB上时,
∵CE2=BE2+BC2=EA2,
∴AE2=(6﹣AE)2+4,
∴AE= ,
∴DE= = = ,
综上所述:DE= 或 ,
故答案为: 或 .
二、选择题(本大题共8小题,每小题只有一个正确选项,每小题4分,共32分)
7.【解答】解:1500000=1.5×106,
故选:C.
8.【解答】解:圆柱体的主视图是长方形,圆锥的主视图是等腰三角形,球的主视图是圆
形,四面体的主视图是三角形,
故选:A.
9.【解答】解:A. ,选项错误;
B.原式=2,选项错误;
C.原式=﹣27a3,选项错误;
D.原式=a6﹣3=a3,选项正确.
故选:D.
10.【解答】解:了解三名学生的视力情况,由于总体数量较少,且容易操作,因此宜采
取普查,因此选项A不符合题意;任意画一个三角形,其内角和是360°是比可能事件,因此选项B不符合题意;
根据平均数和方差的意义可得选项C符合题意;
一个抽奖活动中,中奖概率为 ,表示中奖的可能性为 ,不代表抽奖20次就有1
次中奖,因此选项D不符合题意;
故选:C.
11.【解答】解:∵平行四边形ABCD的对角线AC,BD相交于点O,
∴点O为线段BD的中点.
又∵点E是CD的中点,
∴线段OE为△DBC的中位线,
∴OE∥BC,OE= BC,
∴△DOE∽△DBC,
∴ =( )2= .
故选:B.
12.【解答】解:∵a=(﹣2)1﹣1a,
﹣2a=(﹣2)2﹣1a,
4a=(﹣2)3﹣1a,
﹣8a=(﹣2)4﹣1a,
16a=(﹣2)5﹣1a,
﹣32a=(﹣2)6﹣1a,
…
由上规律可知,第n个单项式为:(﹣2)n﹣1a.
故选:A.
13.【解答】解:设圆椎的底面圆的半径为r,
根据题意可知:
AD=AE=4,∠DAE=45°,
∴2 r= ,
π
解得r= .答:该圆锥的底面圆的半径是 .
故选:D.
14.【解答】解:解不等式组,得
<x≤25,
∵不等式组有且只有45个整数解,
∴﹣20≤ <﹣19,
解得﹣61≤a<﹣58,
因为关于y的方程 + =1的解为:
y=﹣a﹣61,y≤0,
∴﹣a﹣61≤0,
解得a≥﹣61,
∵y+1≠0,∴y≠﹣1,
∴a≠﹣60
则a的值为:﹣61或﹣59.
故选:B.
三、解答题(本大题共9小题,共70分)
15.【解答】解:原式= ÷
= •
= ,
当x= 时,原式=2.
16.【解答】证明:在△ADB和△BCA中,
,
∴△ADB≌△BCA(SSS),
∴∠ADB=∠BCA.17.【解答】解:(1)平均数 k=(7000+4400+2400+2000+1900+1800×3+1200)÷9=
2700,
9个数据从大到小排列后,第5个数据是1900,所以中位数m=1900,
1800出现了三次,次数最多,所以众数n=1800.
故答案为:2700,1900,1800;
(2)由题意可知,辞职的那名员工工资高于2700元,所以辞职的那名员工可能是经理
或副经理.
故答案为:经理或副经理.
18.【解答】解:设原计划每年绿化升级改造的面积是 x万平方米,则实际每年绿化升级
改造的面积是2x万平方米,根据题意,得:
﹣ =4,
解得:x=45,
经检验,x=45是原分式方程的解,
则2x=2×45=90.
答:实际平均每年绿化升级改造的面积是90万平方米.
19.【解答】解:(1)甲家庭选择到大理旅游的概率为 ;
(2)记到大理、丽江、西双版纳三个城市旅游分别为A、B、C,
列表得:
A B C
A (A,A) (A,B) (A,C)
B (B,A) (B,B) (B,C)
C (C,A) (C,B) (C,C)
由表格可知,共有9种等可能性结果,其中甲、乙两个家庭选择到上述三个城市中的同
一个城市旅游的有3种结果,
所以甲、乙两个家庭选择到上述三个城市中的同一个城市旅游的概率P= = .
20.【解答】(1)证明:连接OC.
∵OA=OC,∴∠OAC=∠OCA,
∵AC平分∠DAB,
∴∠CAD=∠CAB,
∴∠DAC=∠ACO,
∴AD∥OC,
∵AD⊥DE,
∴OC⊥DE,
∴直线CE是 O的切线;
(2)连接BC⊙,
∵AB为 O的直径,
∴∠ACB⊙=90°,
∴∠ADC=∠ACB,
∵AC平分∠DAB,
∴∠DAC=∠CAB,
∴△DAC∽△CAB,
∴ = ,
∵cos∠CAB= = ,
∴设AC=4x,AB=5x,
∴ = ,
∴x= ,
∴AB= .21.【解答】解:(1)设大货车、小货车各有x与y辆,
由题意可知: ,
解得: ,
答:大货车、小货车各有12与8辆
(2)设到A地的大货车有x辆,
则到A地的小货车有(10﹣x)辆,
到B地的大货车有(12﹣x)辆,
到B地的小货车有(x﹣2)辆,
∴y=900x+500(10﹣x)+1000(12﹣x)+700(x﹣2)
=100x+15600,
其中2<x<10.
(3)运往A地的物资共有[15x+10(10﹣x)]吨,
15x+10(10﹣x)≥140,
解得:x≥8,
∴8≤x<10,
当x=8时,
y有最小值,此时y=100×8+15600=16400元,
答:总运费最小值为16400元.
22.【解答】解:(1)∵四边形ABCD是菱形,∠BAD=60°,
∴∠ABC=∠ADC=120°,
∵CE⊥AB,CF⊥AD,
∴CE=CF,
∵H为对角线AC的中点,
∴EH=FH= AC,
∵∠CAE=30°,
∵CE= AC,
∴CE=EH=CF=FH,
∴四边形CEHF是菱形;
(2)∵CE⊥AB,CE=4,△ACE的面积为16,∴AE=8,
∴AC= =4 ,
连接BD,则BD⊥AC,AH= AC=2 ,
∵∠AHB=∠AEC=90°,∠BAH=∠EAC,
∴△ABH∽△ACE,
∴ = ,
∴ = ,
∴BH= ,
∴BD=2BH=2 ,
∴菱形ABCD的面积= AC•BD= =20.
23.【解答】解:(1)把A、C点的坐标代入抛物线的解析式得,
,
解得, ;
(2)连接BC,与抛物线的对称轴交于点F,连接AF,如图1,
此时,AF+CF=BF+CF=BC的值最小,
∵AC为定值,
∴此时△AFC的周长最小,
由(1)知,b=﹣2,c=﹣3,
∴抛物线的解析式为:y=x2﹣2x﹣3,
∴对称轴为x=1,令y=0,得y=x2﹣2x﹣3=0,
解得,x=﹣1,或x=3,
∴B(3,0),
令x=0,得y=x2﹣2x﹣3=﹣3,
∴C(0,﹣3),
设直线BC的解析式为:y=kx+b(k≠0),得
,
解得, ,
∴直线BC的解析式为:y=x﹣3,
当x=1时,y=x﹣3=﹣2,
∴F(1,﹣2);
(3)设P(m,m2﹣2m﹣3)(m>3),过P作PH⊥BC于H,过D作DG⊥BC于G,
如图2,
则PH=5DG,E(m,m﹣3),
∴PE=m2﹣3m,DE=m﹣3,
∵∠PHE=∠DGE=90°,∠PEH=∠DEG,
∴△PEH∽△DEG,
∴ ,
∴ ,
∵m=3(舍),或m=5,∴点P的坐标为P(5,12).
故存在点P,使点P到直线BC的距离是点D到直线BC的距离的5倍,其P点坐标为
(5,12).