文档内容
2020年北京市高级中等学校招生考试
数学试卷
一、选择题(本题共16分,每小题2分)第1-8题均有四个选项,符合题意的选项只有一个.
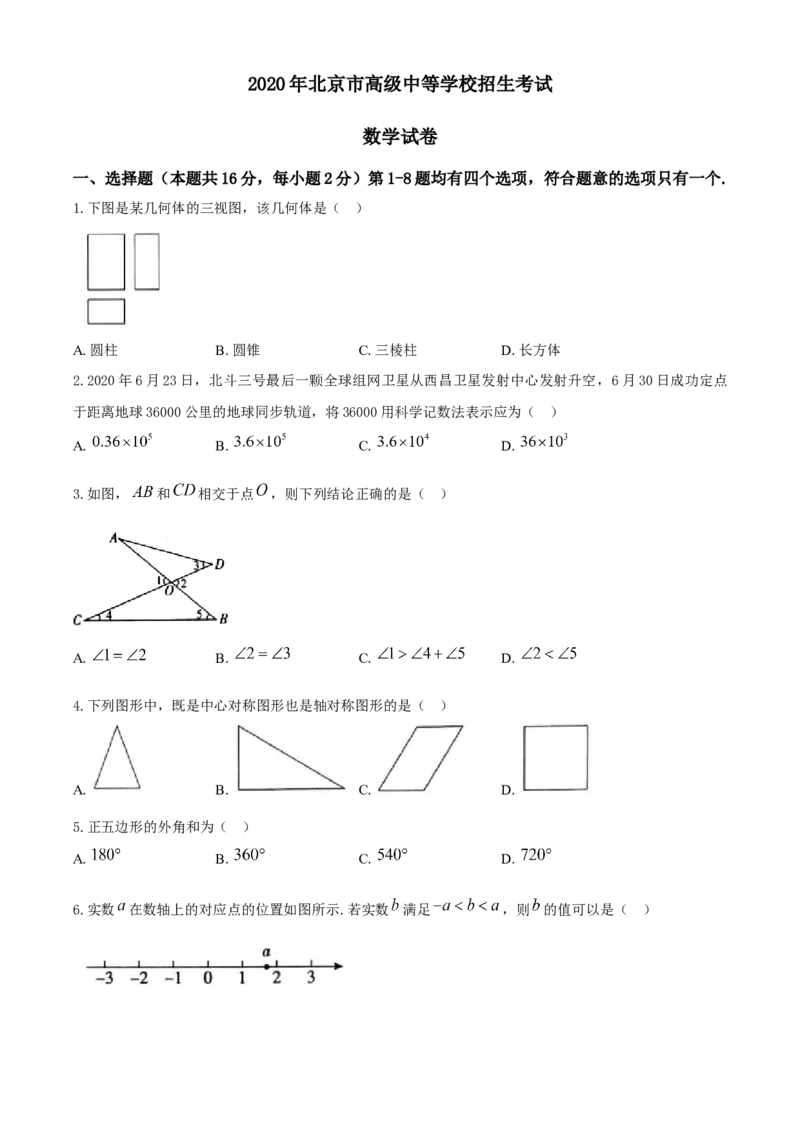
1.下图是某几何体的三视图,该几何体是( )
A.圆柱 B.圆锥 C.三棱柱 D.长方体
2.2020年6月23日,北斗三号最后一颗全球组网卫星从西昌卫星发射中心发射升空,6月30日成功定点
于距离地球36000公里的地球同步轨道,将36000用科学记数法表示应为( )
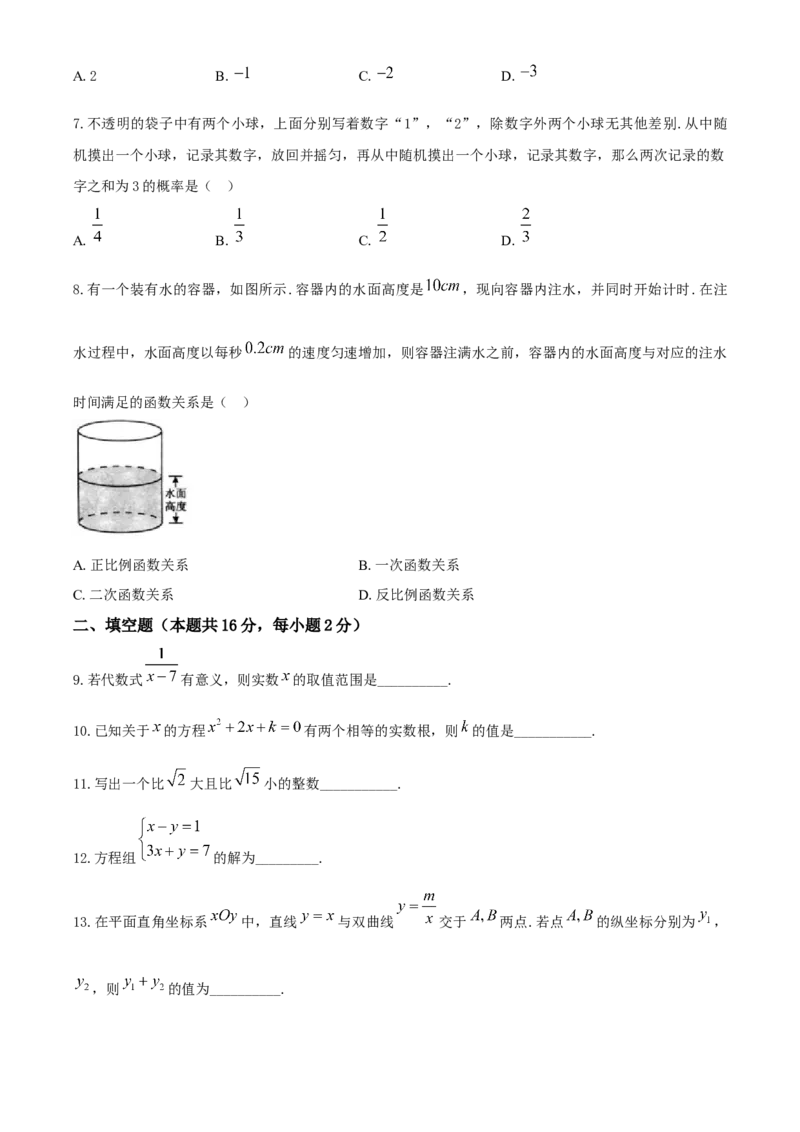
A. B. C. D.
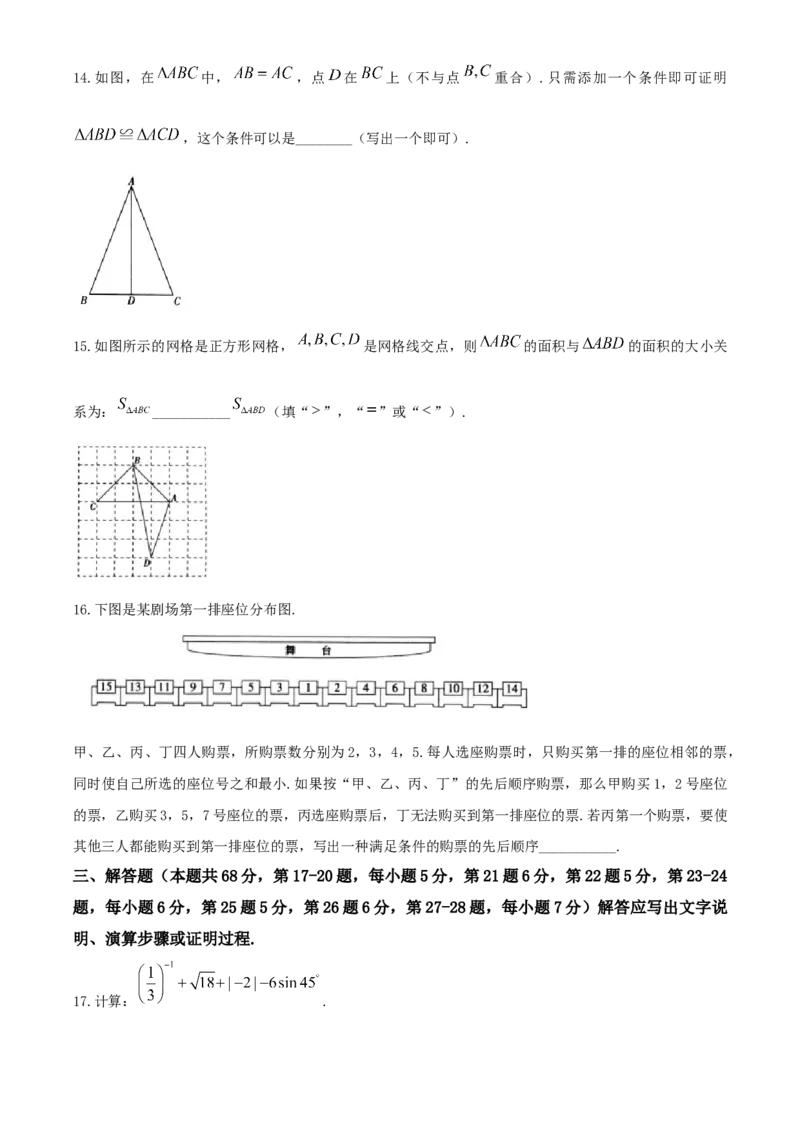
3.如图, 和 相交于点 ,则下列结论正确的是( )
A. B. C. D.
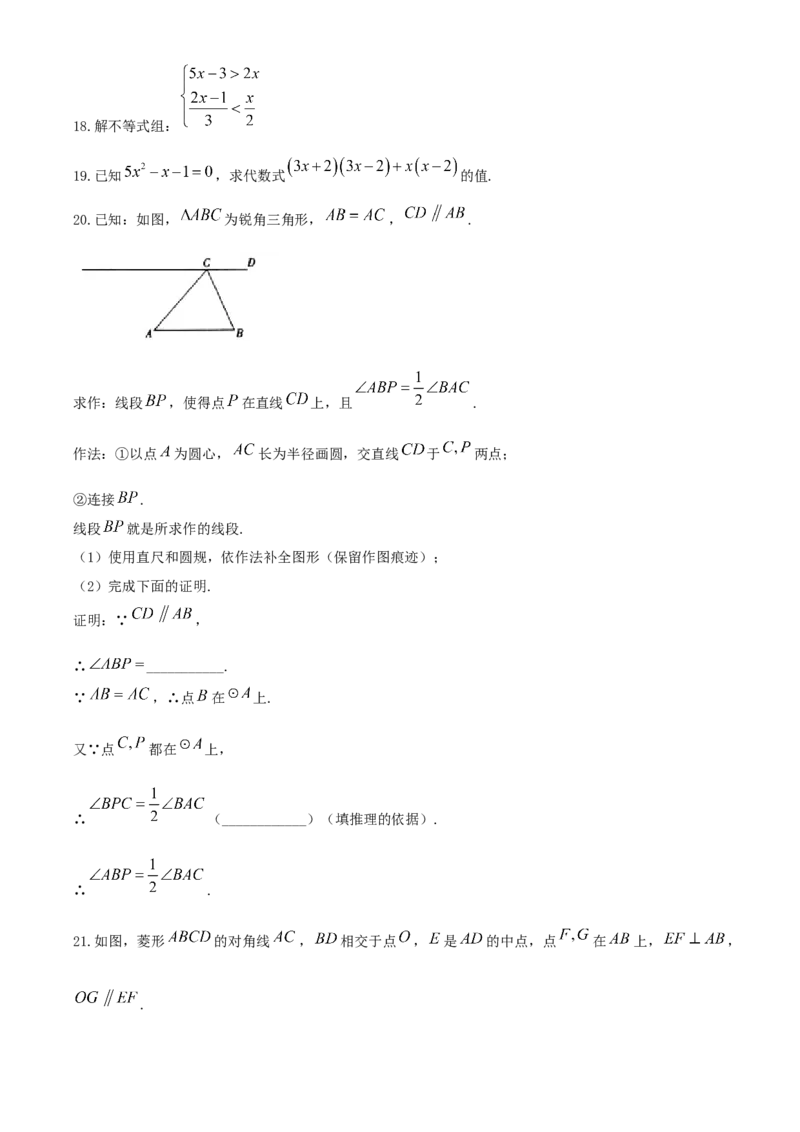
4.下列图形中,既是中心对称图形也是轴对称图形的是( )
A. B. C. D.
5.正五边形的外角和为( )
A. B. C. D.
6.实数 在数轴上的对应点的位置如图所示.若实数 满足 ,则 的值可以是( )A.2 B. C. D.
7.不透明的袋子中有两个小球,上面分别写着数字“1”,“2”,除数字外两个小球无其他差别.从中随
机摸出一个小球,记录其数字,放回并摇匀,再从中随机摸出一个小球,记录其数字,那么两次记录的数
字之和为3的概率是( )
A. B. C. D.
8.有一个装有水的容器,如图所示.容器内的水面高度是 ,现向容器内注水,并同时开始计时.在注
水过程中,水面高度以每秒 的速度匀速增加,则容器注满水之前,容器内的水面高度与对应的注水
时间满足的函数关系是( )
A.正比例函数关系 B.一次函数关系
C.二次函数关系 D.反比例函数关系
二、填空题(本题共16分,每小题2分)
9.若代数式 有意义,则实数 的取值范围是__________.
10.已知关于 的方程 有两个相等的实数根,则 的值是___________.
11.写出一个比 大且比 小的整数___________.
12.方程组 的解为_________.
13.在平面直角坐标系 中,直线 与双曲线 交于 两点.若点 的纵坐标分别为 ,
,则 的值为__________.14.如图,在 中, ,点 在 上(不与点 重合).只需添加一个条件即可证明
,这个条件可以是________(写出一个即可).
15.如图所示的网格是正方形网格, 是网格线交点,则 的面积与 的面积的大小关
系为: ___________ (填“ ”,“ ”或“ ”).
16.下图是某剧场第一排座位分布图.
甲、乙、丙、丁四人购票,所购票数分别为2,3,4,5.每人选座购票时,只购买第一排的座位相邻的票,
同时使自己所选的座位号之和最小.如果按“甲、乙、丙、丁”的先后顺序购票,那么甲购买1,2号座位
的票,乙购买3,5,7号座位的票,丙选座购票后,丁无法购买到第一排座位的票.若丙第一个购票,要使
其他三人都能购买到第一排座位的票,写出一种满足条件的购票的先后顺序___________.
三、解答题(本题共68分,第17-20题,每小题5分,第21题6分,第22题5分,第23-24
题,每小题6分,第25题5分,第26题6分,第27-28题,每小题7分)解答应写出文字说
明、演算步骤或证明过程.
17.计算: .18.解不等式组:
19.已知 ,求代数式 的值.
20.已知:如图, 为锐角三角形, , .
求作:线段 ,使得点 在直线 上,且 .
作法:①以点 为圆心, 长为半径画圆,交直线 于 两点;
②连接 .
线段 就是所求作的线段.
(1)使用直尺和圆规,依作法补全图形(保留作图痕迹);
(2)完成下面的证明.
证明:∵ ,
∴ ___________.
∵ ,∴点 在 上.
又∵点 都在 上,
∴ (____________)(填推理的依据).
∴ .
21.如图,菱形 的对角线 , 相交于点 , 是 的中点,点 在 上, ,
.(1)求证:四边形 是矩形;
(2)若 , ,求 和 的长.
22.在平面直角坐标系 中,一次函数 的图象由函数 的图象平移得到,且经过
点 .
(1)求这个一次函数的解析式;
(2)当 时,对于 的每一个值,函数 的值大于一次函数 的值,直接写出
的取值范围.
23.如图, 为 的直径, 为 延长线上一点, 是 的切线, 为切点, 于点
,交 于点 .
(1)求证: ;
(2)若 , ,求 的长.
24.小云在学习过程中遇到一个函数 .
下面是小云对其探究的过程,请补充完整:
(1)当 时,对于函数 ,即 ,当 时, 随 的增大而_______,且 ;
对于函数 ,当 时, 随 的增大而__________,且 ;
结合上述分析,进一步探究发现,对于函数 ,当 时, 随 的增大而__________.
(2)当 时,
对于函数 ,当 时, 与 的几组对应值如下表:
0 1 2 3 …
0 1 …
结合上表,进一步探究发现,当 时, 随 的增大而增大.在平面直角坐标系 中,画出当
时的函数 的图象.
(3)过点 作平行于 轴的直线 ,结合(1)(2)的分析,解决问题:若直线 与函数
的图象有两个交点,则 的最大值是____________.
25.小云统计了自己所住小区5月1日至30日的厨余垃圾分出量(单位:千克),相关信息如下:
.小云所住小区5月1日至30日的厨余垃圾分出量统计图:.小云所住小区5月1日至30日分时段的厨余垃圾分出量的平均数如下:
时段 1日至10日 11日至20日 21日至30日
平均数 100 170 250
(1)该小区5月1日至30日的厨余垃圾分出量的平均数约为___________(结果取整数);
(2)已知该小区4月的厨余垃圾分出量的平均数为60,则该小区5月1日至30日的厨余垃圾分出量的平
均数约为4月的__________倍(结果保留小数点后一位);
(3)记该小区5月1日至10日的厨余垃圾分出量的方差为 ,5月11日至20日的厨余垃圾分出量的方
差为 ,5月21日至30日的厨余垃圾分出量的方差为 .直接写出 , , 的大小关系.
26.在平面直角坐标系 中, , 为抛物线 上任意两点,其
中 .
(1)若抛物线的对称轴为 ,当 , 为何值时, ;
(2)设抛物线的对称轴为 .若对于 ,都有 ,求 的取值范围.
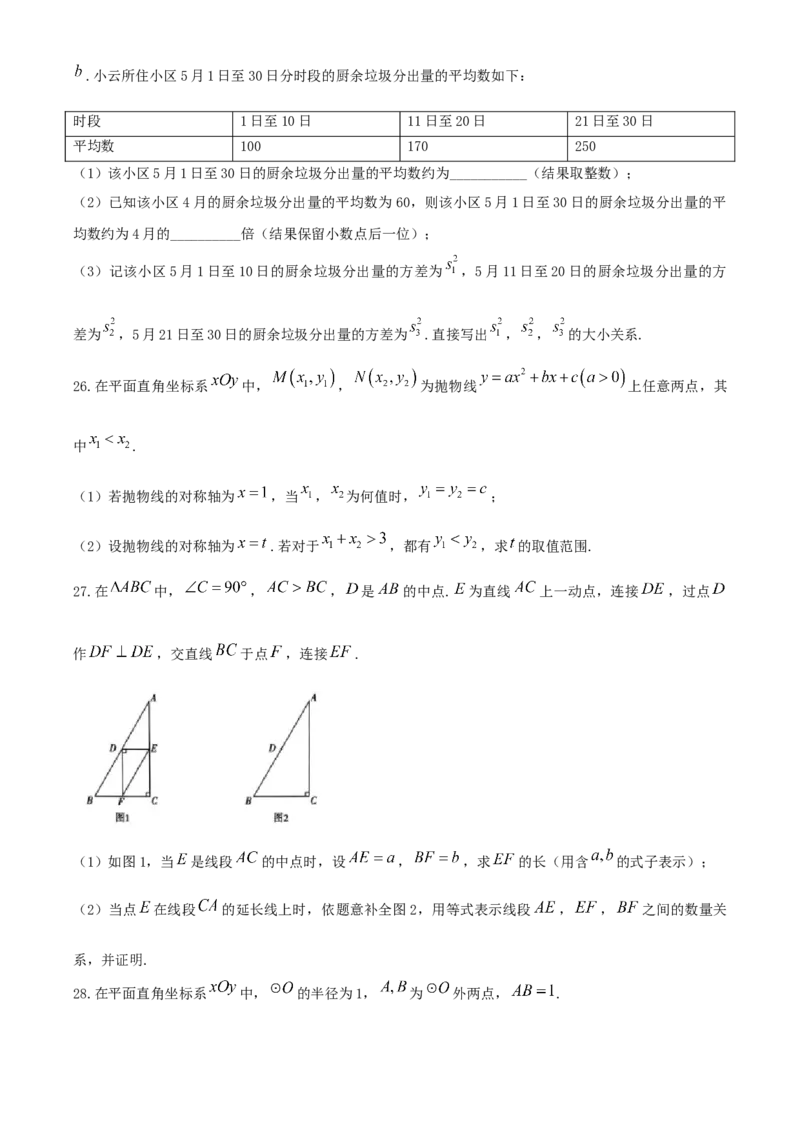
27.在 中, , , 是 的中点. 为直线 上一动点,连接 ,过点
作 ,交直线 于点 ,连接 .
(1)如图1,当 是线段 的中点时,设 , ,求 的长(用含 的式子表示);
(2)当点 在线段 的延长线上时,依题意补全图2,用等式表示线段 , , 之间的数量关
系,并证明.
28.在平面直角坐标系 中, 的半径为1, 为 外两点, .给出如下定义:平移线段 ,得到 的弦 ( , 分别为点 的对应点),线段 长度
的最小值称为线段 到 的“平移距离”.
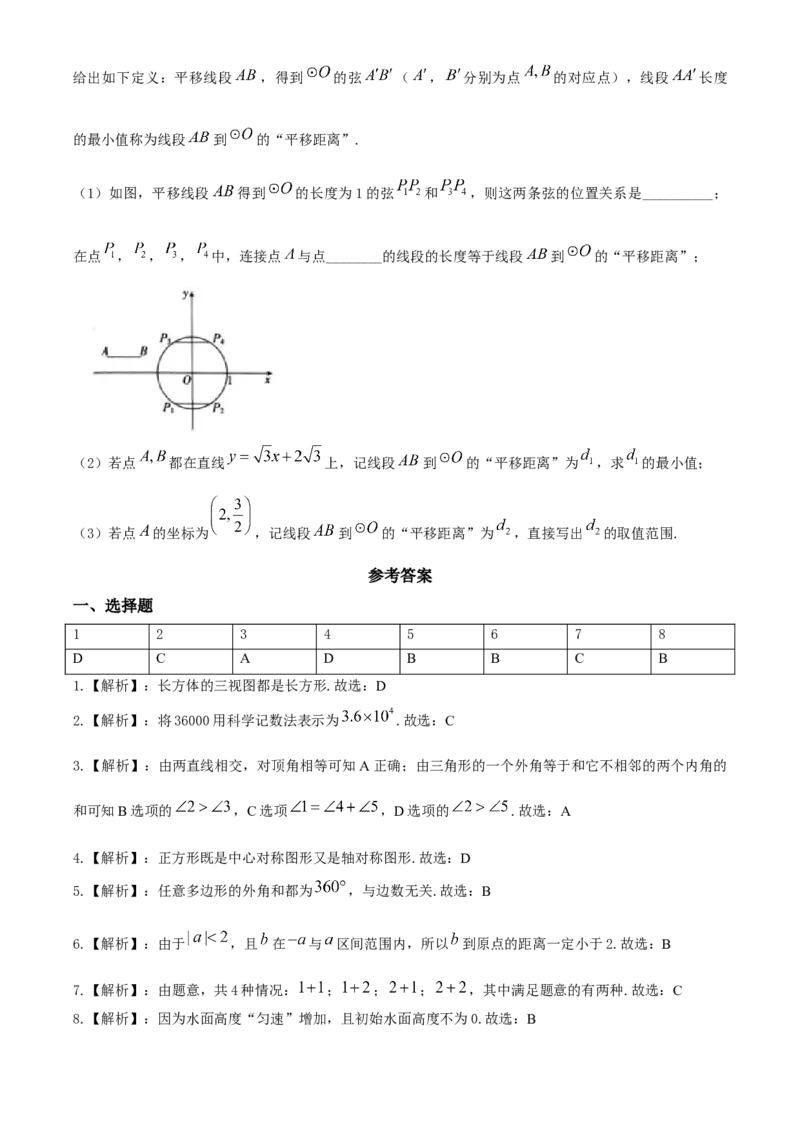
(1)如图,平移线段 得到 的长度为1的弦 和 ,则这两条弦的位置关系是__________;
在点 , , , 中,连接点 与点________的线段的长度等于线段 到 的“平移距离”;
(2)若点 都在直线 上,记线段 到 的“平移距离”为 ,求 的最小值;
(3)若点 的坐标为 ,记线段 到 的“平移距离”为 ,直接写出 的取值范围.
参考答案
一、选择题
1 2 3 4 5 6 7 8
D C A D B B C B
1.【解析】:长方体的三视图都是长方形.故选:D
2.【解析】:将36000用科学记数法表示为 .故选:C
3.【解析】:由两直线相交,对顶角相等可知A正确;由三角形的一个外角等于和它不相邻的两个内角的
和可知B选项的 ,C选项 ,D选项的 .故选:A
4.【解析】:正方形既是中心对称图形又是轴对称图形.故选:D
5.【解析】:任意多边形的外角和都为 ,与边数无关.故选:B
6.【解析】:由于 ,且 在 与 区间范围内,所以 到原点的距离一定小于2.故选:B
7.【解析】:由题意,共4种情况: ; ; ; ,其中满足题意的有两种.故选:C
8.【解析】:因为水面高度“匀速”增加,且初始水面高度不为0.故选:B二、填空题
9. 10.1 11.3 12. 13.0
14. 为 中点 15. 16.丙,丁,甲,乙
9.【解析】:分母不能为0.
10.【解析】:由题意: .所以 .
11.【解析】:答案不唯一,2或3都对
12.【解析】:略.
13.【解析】:根据一次函数 与反比例函数交点关于原点对称,所以 .
14.【解析】:答案不唯一:因为 为 中点,所以 , , .
所以 .
15.【解析】:由网格可求 , .所以面积相等.
16.【解析】:答案不唯一;丙先选择:1,2,3,4.丁选:5,7,9,11,13.甲选:6,8.乙选:10,
12,14.所以顺序为丙,丁,甲,乙.
三、解答题
17.【解析】:解:原式
18.【解析】:解:解①式得: ,解②式得:
∴此不等式组的解集为
19.【解析】:解:原式
∵ ∴ ∴
∴原式
20.【解析】:
(1)如图所示(2) ;在同圆或等圆中同弧所对的圆周角等于它所对圆心角的一半.
21【解析】:
(1)∵四边形 为菱形∴点 为 中点
∵点 为 中点∴ 为 的中位线
∴ ∵
∴四边形 为平行四边形
∵
∴平行四边形 为矩形
(2)∵点 为 中点,
∴ ∵ ,
∴在 中,
∵四边形 为菱形
∴ ∴
∵四边形 为矩形∴
∴
22.【解析】(1)∵一次函数 且由 平移得到
∴将点 代入 可得
∴一次函数的解析式为
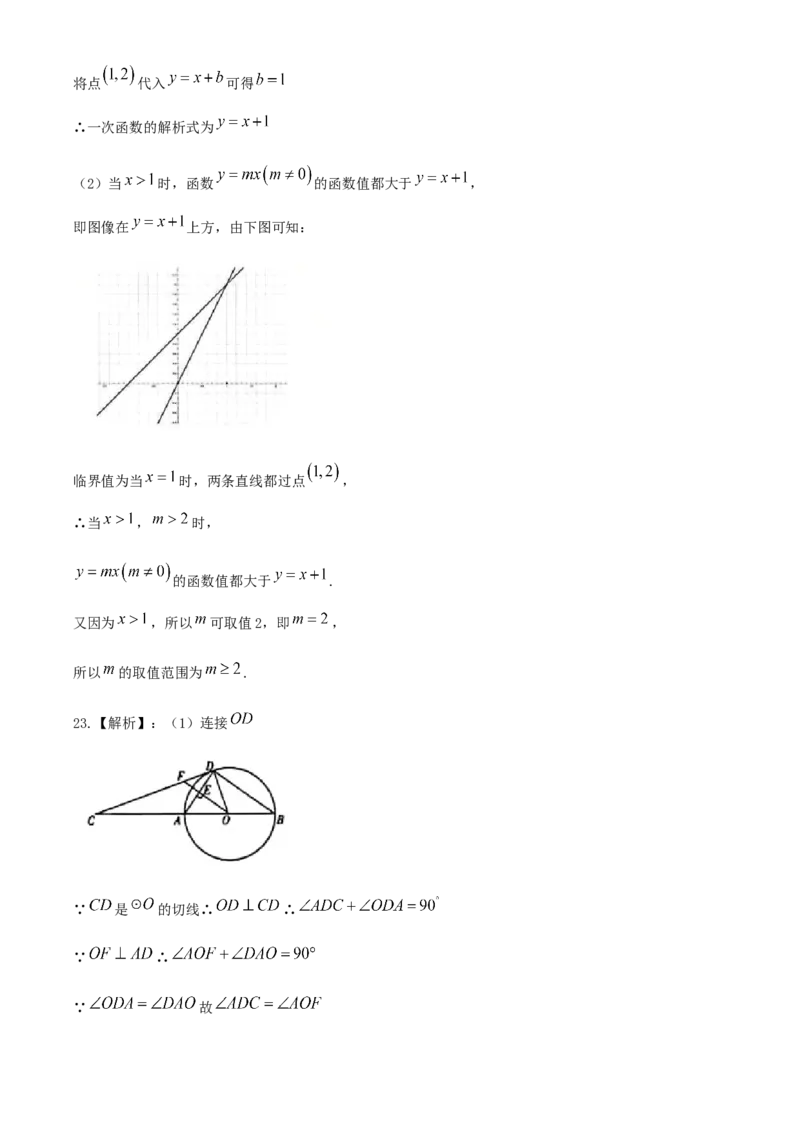
(2)当 时,函数 的函数值都大于 ,
即图像在 上方,由下图可知:
临界值为当 时,两条直线都过点 ,
∴当 , 时,
的函数值都大于 .
又因为 ,所以 可取值2,即 ,
所以 的取值范围为 .
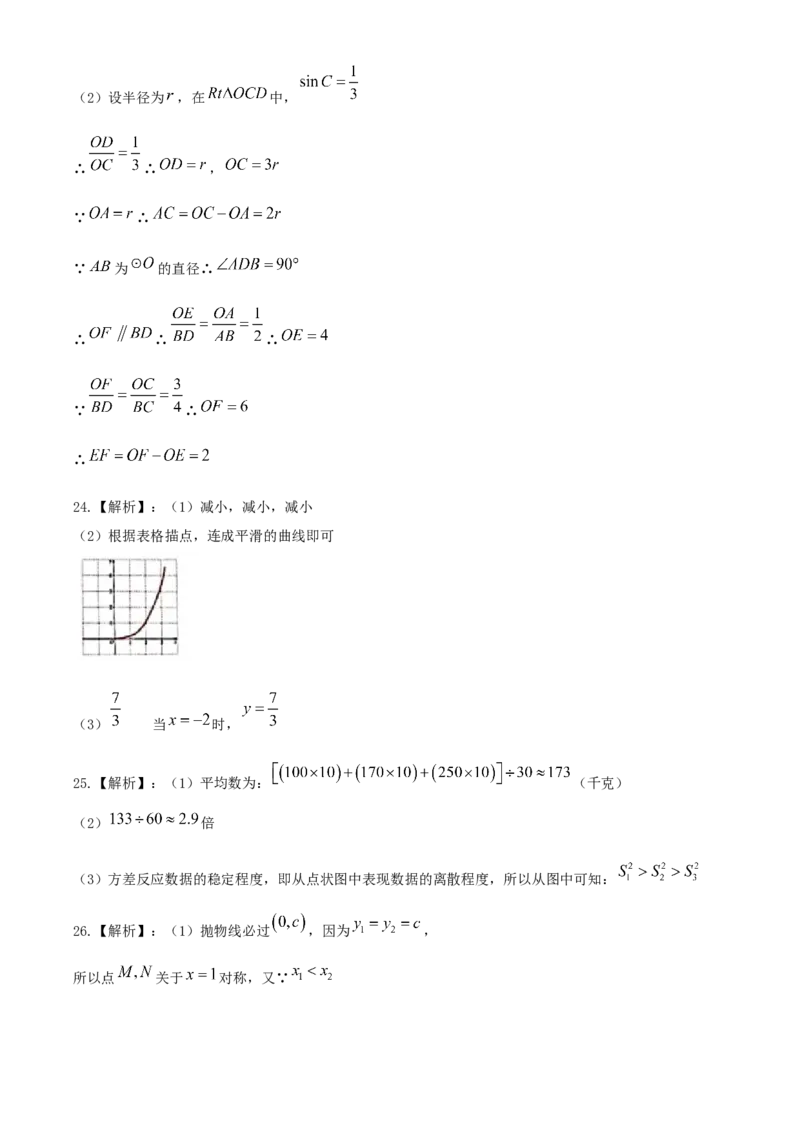
23.【解析】:(1)连接
∵ 是 的切线∴ ∴
∵ ∴
∵ 故(2)设半径为 ,在 中,
∴ ∴ ,
∵ ∴
∵ 为 的直径∴
∴ ∴ ∴
∵ ∴
∴
24.【解析】:(1)减小,减小,减小
(2)根据表格描点,连成平滑的曲线即可
(3) 当 时,
25.【解析】:(1)平均数为: (千克)
(2) 倍
(3)方差反应数据的稳定程度,即从点状图中表现数据的离散程度,所以从图中可知:
26.【解析】:(1)抛物线必过 ,因为 ,
所以点 关于 对称,又∵∴ ,
(2)情况1:当 , 恒成立
情况2:当 , , 恒不成立
情况3:当 , ,要 ,必有 ,
∴ ,∴
27.【解析】:(1)∵ 是 的中点, 是线段 的中点
∴ 为 的中位线∴
∵ ∴
∵ ∴
∴四边形 为矩形.
∴ ,∴ ,∴
∴
(2)过点 作 的平行线交 延长线于点 ,连接
∵ ∴ ,
∵ 是 的中点∴ ∴
∴ ,
∵ ∴ 是线段 的垂直平分线
∴∵ , ∴ ,
在 中,
∴
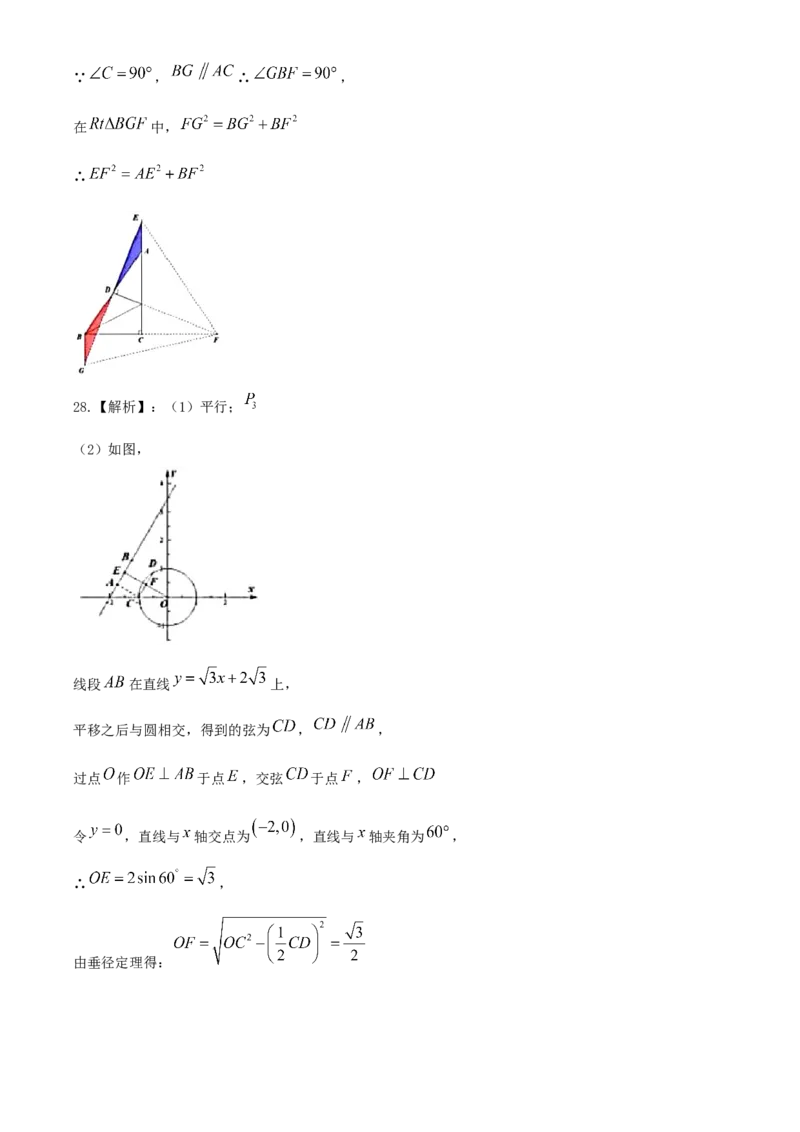
28.【解析】:(1)平行;
(2)如图,
线段 在直线 上,
平移之后与圆相交,得到的弦为 , ,
过点 作 于点 ,交弦 于点 ,
令 ,直线与 轴交点为 ,直线与 轴夹角为 ,
∴ ,
由垂径定理得:∴
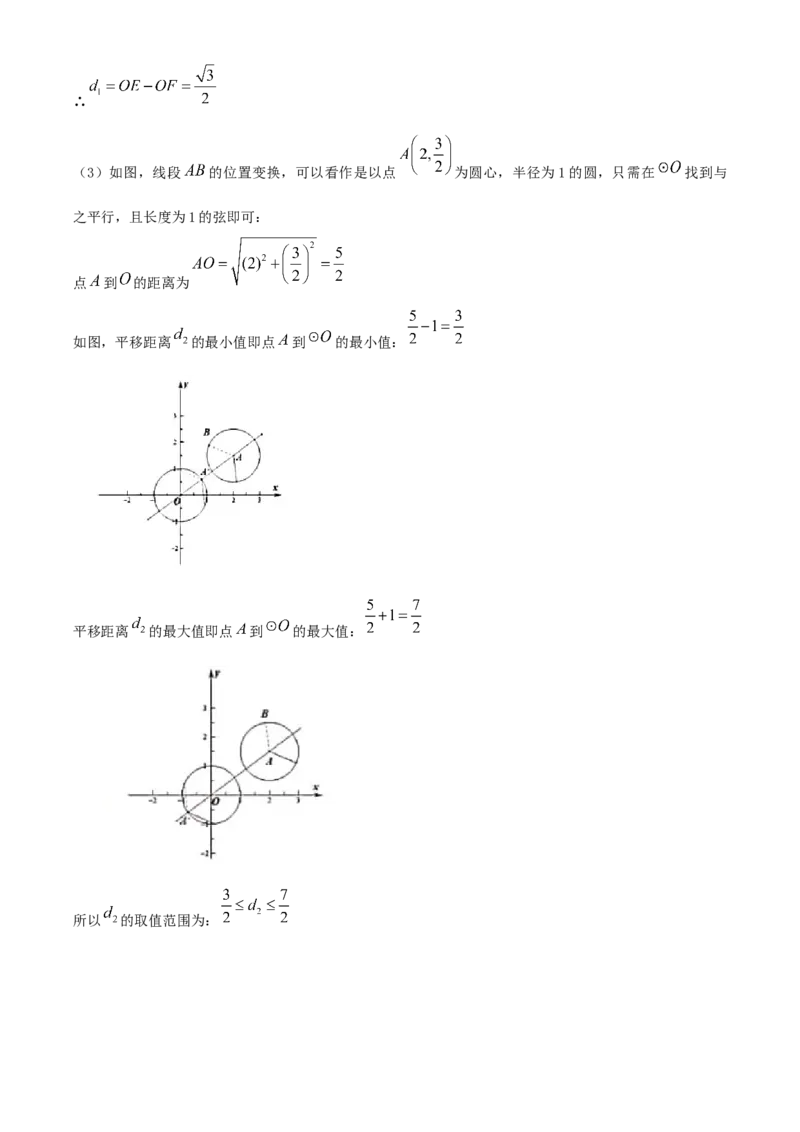
(3)如图,线段 的位置变换,可以看作是以点 为圆心,半径为1的圆,只需在 找到与
之平行,且长度为1的弦即可:
点 到 的距离为
如图,平移距离 的最小值即点 到 的最小值:
平移距离 的最大值即点 到 的最大值:
所以 的取值范围为: