文档内容
2020年山东省菏泽市中考数学试卷
一、选择题(本大题共8个小题,每小题3分,共24分,在每小题给出的四个选项中,只有一
个选项是正确的,请把正确选项的序号涂在答题卡的相应位置.)
1.(3分)下列各数中,绝对值最小的数是( )
A.﹣5 B. C.﹣1 D.
2.(3分)函数y= 的自变量x的取值范围是( )
A.x≠5 B.x>2且x≠5 C.x≥2 D.x≥2且x≠5
3.(3分)在平面直角坐标系中,将点P(﹣3,2)向右平移3个单位得到点P',则点P'关于x轴
的对称点的坐标为( )
A.(0,﹣2) B.(0,2) C.(﹣6,2) D.(﹣6,﹣2)
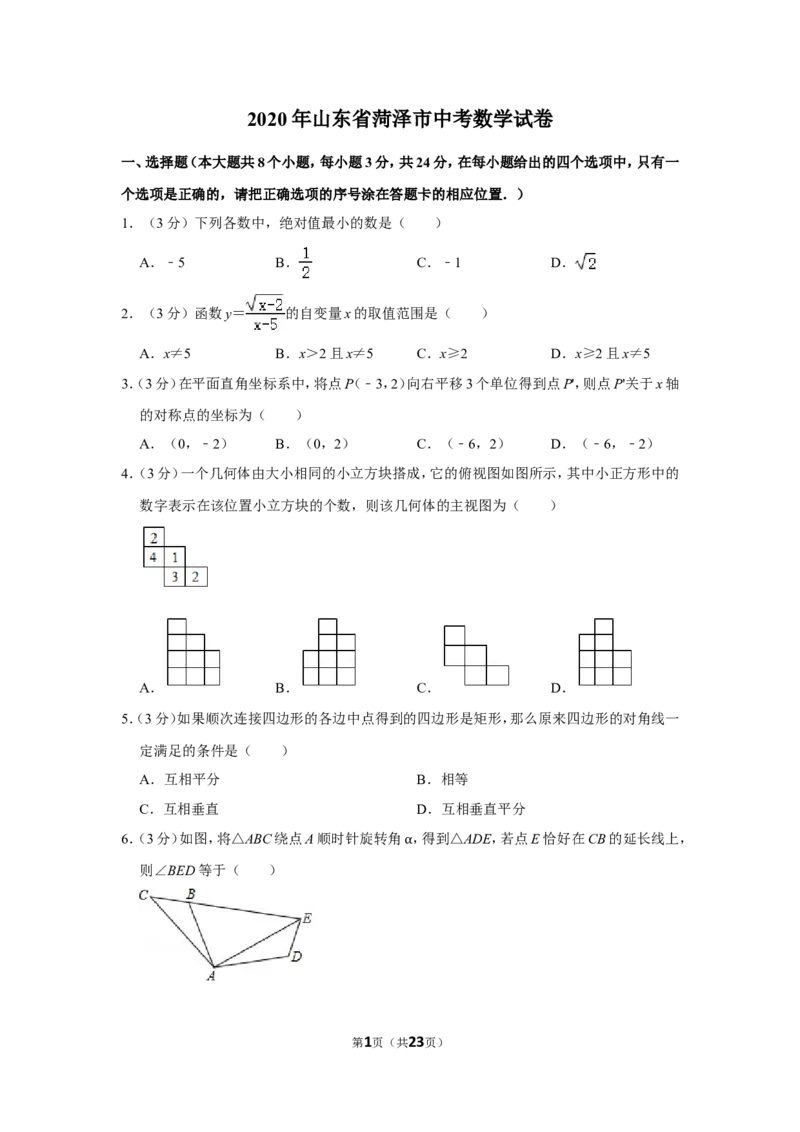
4.(3分)一个几何体由大小相同的小立方块搭成,它的俯视图如图所示,其中小正方形中的
数字表示在该位置小立方块的个数,则该几何体的主视图为( )
A. B. C. D.
5.(3分)如果顺次连接四边形的各边中点得到的四边形是矩形,那么原来四边形的对角线一
定满足的条件是( )
A.互相平分 B.相等
C.互相垂直 D.互相垂直平分
6.(3分)如图,将△ABC绕点A顺时针旋转角 ,得到△ADE,若点E恰好在CB的延长线上,
则∠BED等于( ) α
第1页(共23页)A. B. C. D.180°﹣
α α α
7.(3分)等腰三角形的一边长是3,另两边的长是关于x的方程x2﹣4x+k=0的两个根,则k
的值为( )
A.3 B.4 C.3或4 D.7
8.(3分)一次函数y=acx+b与二次函数y=ax2+bx+c在同一平面直角坐标系中的图象可能
是( )
A. B.
C. D.
二、填空题(本大题共6个小题,每小题3分,共18分,只要求把最后结果填写在答题卡的相
应区域内.)
9.(3分)计算( ﹣4)( +4)的结果是 .
10.(3分)方程 的解是 .
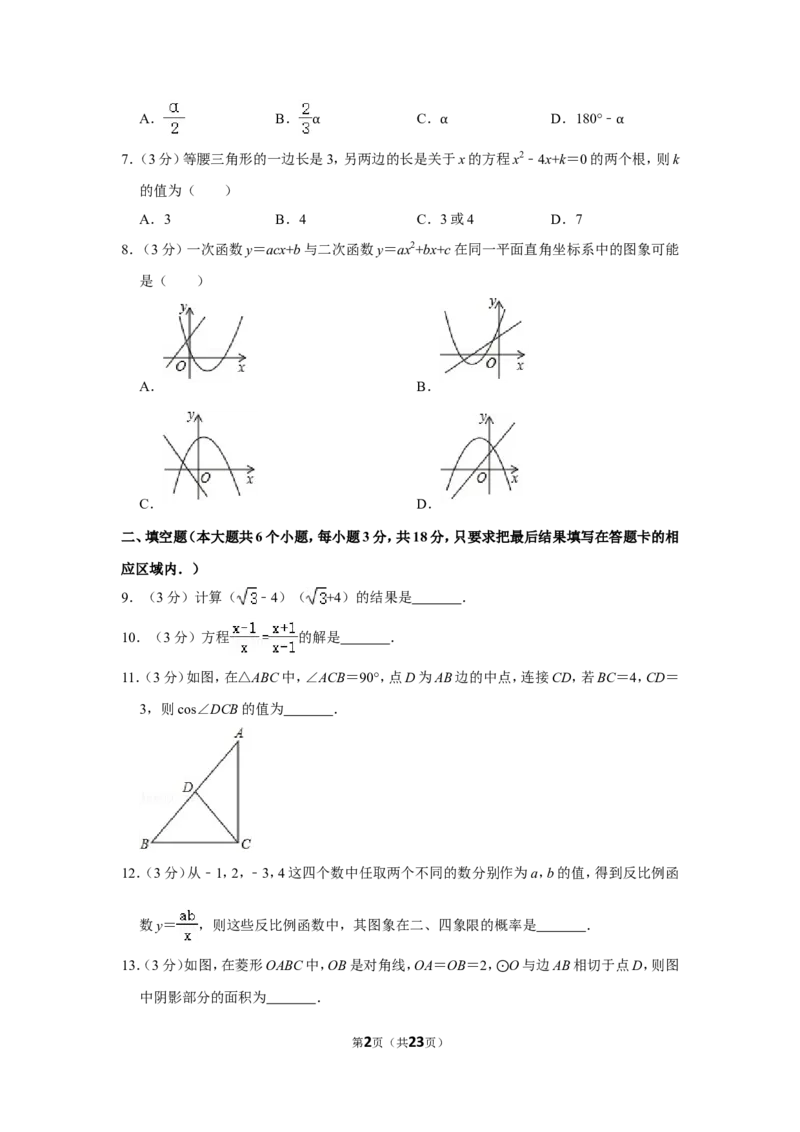
11.(3分)如图,在△ABC中,∠ACB=90°,点D为AB边的中点,连接CD,若BC=4,CD=
3,则cos∠DCB的值为 .
12.(3分)从﹣1,2,﹣3,4这四个数中任取两个不同的数分别作为a,b的值,得到反比例函
数y= ,则这些反比例函数中,其图象在二、四象限的概率是 .
13.(3分)如图,在菱形OABC中,OB是对角线,OA=OB=2, O与边AB相切于点D,则图
中阴影部分的面积为 . ⊙
第2页(共23页)14.(3分)如图,矩形ABCD中,AB=5,AD=12,点P在对角线BD上,且BP=BA,连接AP
并延长,交DC的延长线于点Q,连接BQ,则BQ的长为 .
三、解答题(本题共78分,把解答或证明过程写在答题卡的相应区域内.)
15.计算:2﹣1+| ﹣3|+2 sin45°﹣(﹣2)2020•( )2020.
16.先化简,再求值:(2a﹣ )÷ ,其中a满足a2+2a﹣3=0.
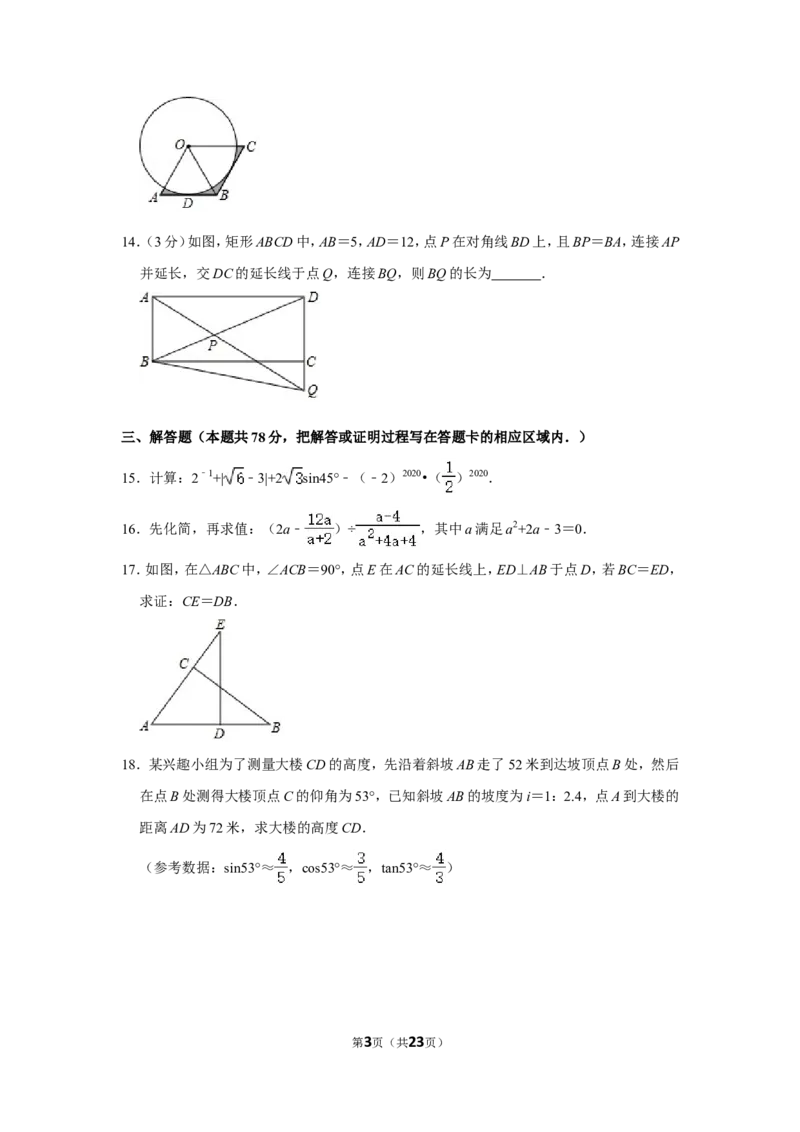
17.如图,在△ABC中,∠ACB=90°,点E在AC的延长线上,ED⊥AB于点D,若BC=ED,
求证:CE=DB.
18.某兴趣小组为了测量大楼CD的高度,先沿着斜坡AB走了52米到达坡顶点B处,然后
在点B处测得大楼顶点C的仰角为53°,已知斜坡AB的坡度为i=1:2.4,点A到大楼的
距离AD为72米,求大楼的高度CD.
(参考数据:sin53°≈ ,cos53°≈ ,tan53°≈ )
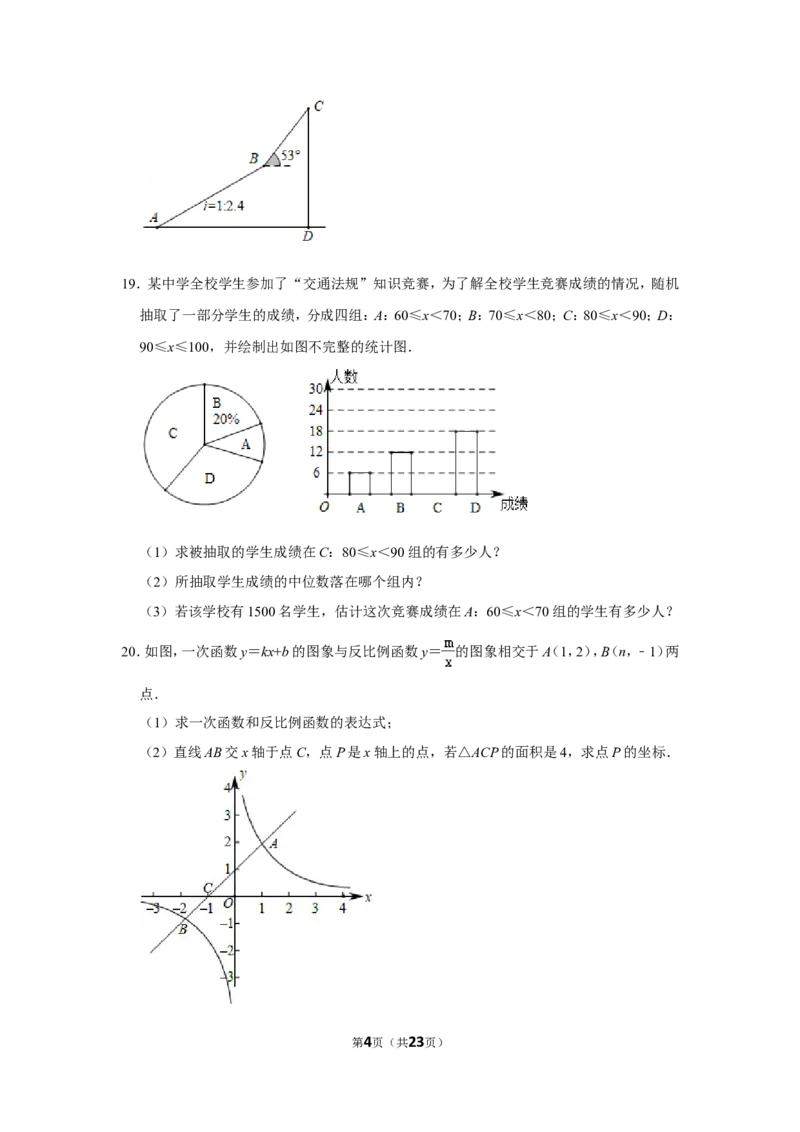
第3页(共23页)19.某中学全校学生参加了“交通法规”知识竞赛,为了解全校学生竞赛成绩的情况,随机
抽取了一部分学生的成绩,分成四组:A:60≤x<70;B:70≤x<80;C:80≤x<90;D:
90≤x≤100,并绘制出如图不完整的统计图.
(1)求被抽取的学生成绩在C:80≤x<90组的有多少人?
(2)所抽取学生成绩的中位数落在哪个组内?
(3)若该学校有1500名学生,估计这次竞赛成绩在A:60≤x<70组的学生有多少人?
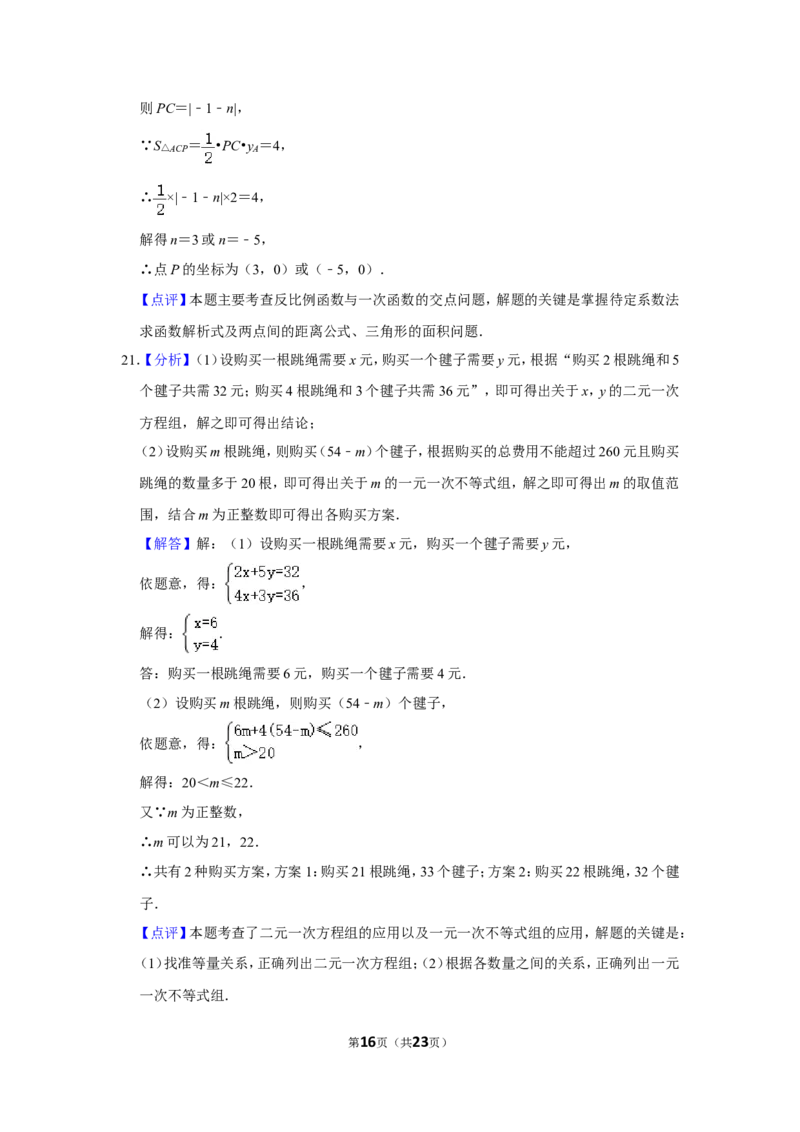
20.如图,一次函数y=kx+b的图象与反比例函数y= 的图象相交于A(1,2),B(n,﹣1)两
点.
(1)求一次函数和反比例函数的表达式;
(2)直线AB交x轴于点C,点P是x轴上的点,若△ACP的面积是4,求点P的坐标.
第4页(共23页)21.今年史上最长的寒假结束后,学生复学,某学校为了增强学生体质,鼓励学生在不聚集的
情况下加强体育锻炼,决定让各班购买跳绳和毽子作为活动器材.已知购买2根跳绳和5
个毽子共需32元;购买4根跳绳和3个毽子共需36元.
(1)求购买一根跳绳和一个毽子分别需要多少元?
(2)某班需要购买跳绳和毽子的总数量是54,且购买的总费用不能超过260元;若要求购
买跳绳的数量多于20根,通过计算说明共有哪几种购买跳绳的方案.
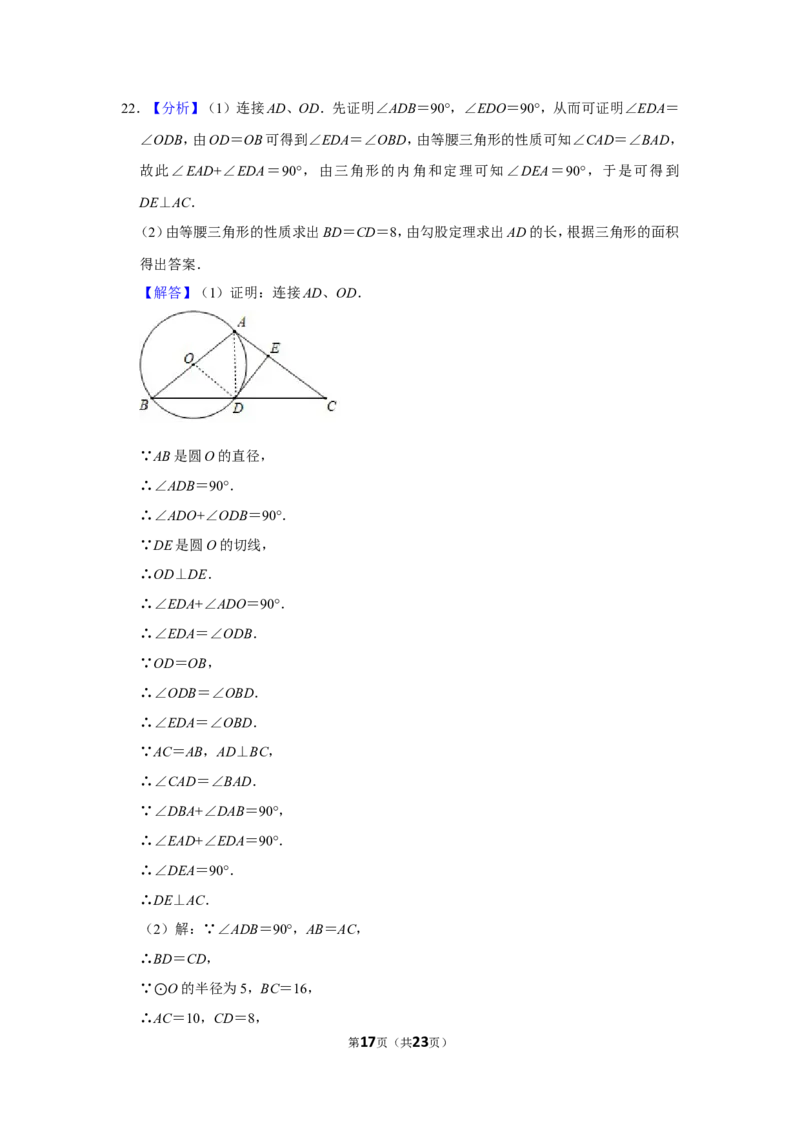
22.如图,在△ABC中,AB=AC,以AB为直径的 O与BC相交于点D,过点D作 O的切
线交AC于点E. ⊙ ⊙
(1)求证:DE⊥AC;
(2)若 O的半径为5,BC=16,求DE的长.
⊙
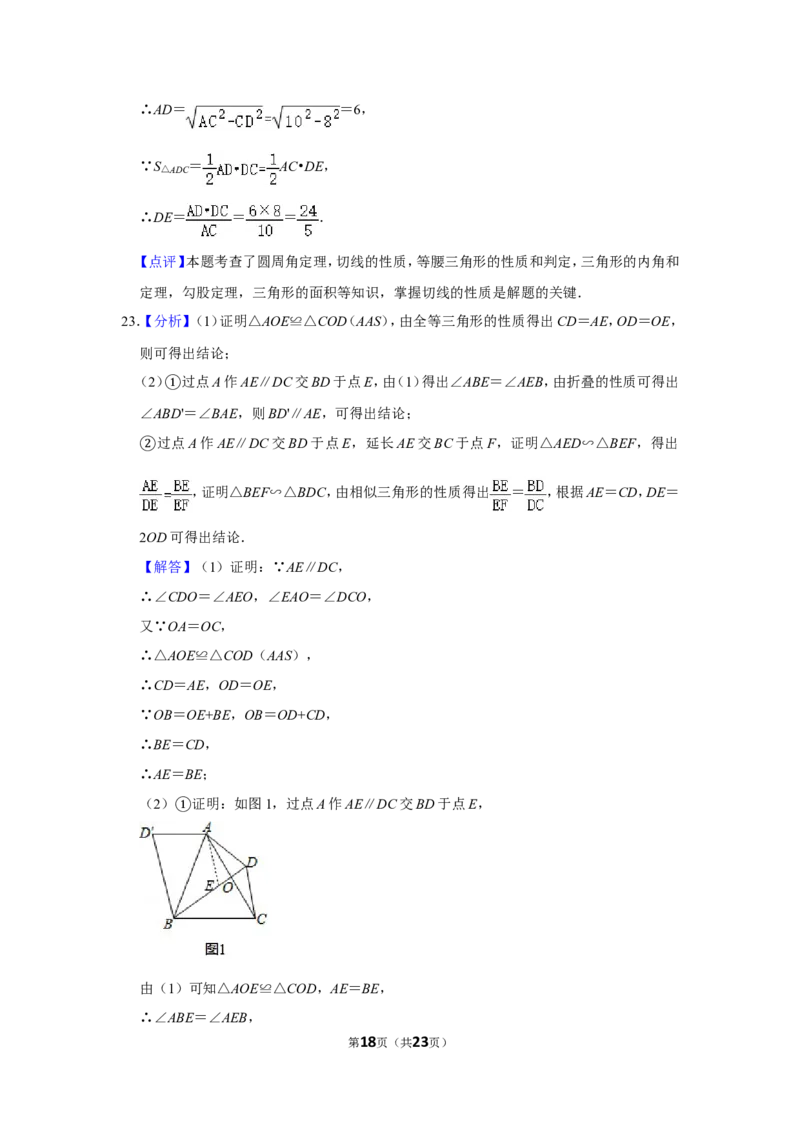
23.如图1,四边形ABCD的对角线AC,BD相交于点O,OA=OC,OB=OD+CD.
(1)过点A作AE∥DC交BD于点E,求证:AE=BE;
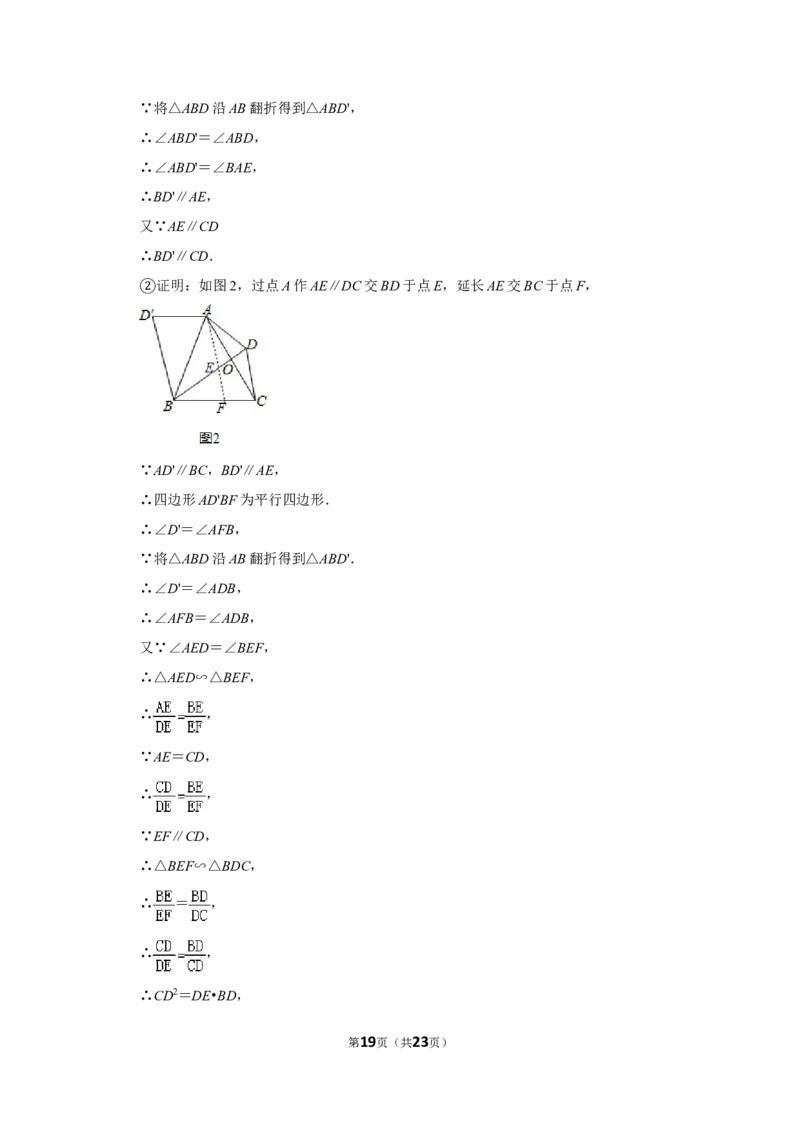
(2)如图2,将△ABD沿AB翻折得到△ABD'.
求证:BD'∥CD;
①若AD'∥BC,求证:CD2=2OD•BD.
②
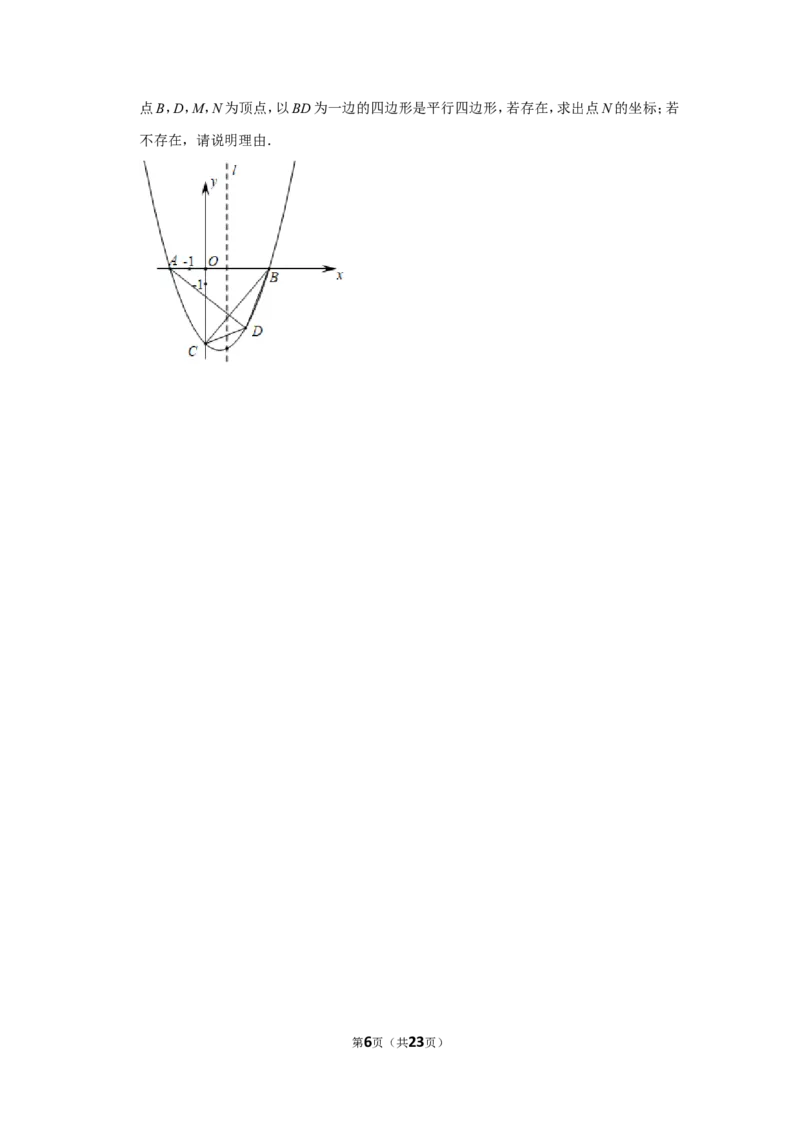
24.如图,抛物线y=ax2+bx﹣6与x轴相交于A,B两点,与y轴相交于点C,OA=2,OB=4,
直线l是抛物线的对称轴,在直线l右侧的抛物线上有一动点D,连接AD,BD,BC,CD.
(1)求抛物线的函数表达式;
(2)若点D在x轴的下方,当△BCD的面积是 时,求△ABD的面积;
(3)在(2)的条件下,点M是x轴上一点,点N是抛物线上一动点,是否存在点N,使得以
第5页(共23页)点B,D,M,N为顶点,以BD为一边的四边形是平行四边形,若存在,求出点N的坐标;若
不存在,请说明理由.
第6页(共23页)2020年山东省菏泽市中考数学试卷
参考答案与试题解析
一、选择题(本大题共8个小题,每小题3分,共24分,在每小题给出的四个选项中,只有一
个选项是正确的,请把正确选项的序号涂在答题卡的相应位置.)
1.【分析】根据绝对值的意义,计算出各选项的绝对值,然后再比较大小即可.
【解答】解:∵|﹣5|=5,| |= ,|﹣1|=1,| |= ,
∴绝对值最小的数是 .
故选:B.
【点评】本题考查的是实数的大小比较,熟知绝对值的性质是解答此题的关键.
2.【分析】根据被开方数大于等于0,分母不等于0列式计算即可得解.
【解答】解:由题意得x﹣2≥0且x﹣5≠0,
解得x≥2且x≠5.
故选:D.
【点评】本题考查的知识点为:分式有意义,分母不为0;二次根式的被开方数是非负数.
3.【分析】先根据向右平移3个单位,横坐标加3,纵坐标不变,求出点P'的坐标,再根据关于
x轴对称,横坐标不变,纵坐标相反解答.
【解答】解:∵将点P(﹣3,2)向右平移3个单位得到点P',
∴点P'的坐标是(0,2),
∴点P'关于x轴的对称点的坐标是(0,﹣2).
故选:A.
【点评】本题考查了坐标与图形变化﹣平移,以及关于x轴、y轴对称点的坐标的关系,熟
练掌握并灵活运用是解题的关键.
4.【分析】从正面看,注意“长对正,宽相等、高平齐”,根据所放置的小立方体的个数画出
图形即可.
【解答】解:从正面看所得到的图形为 .
故选:A.
第7页(共23页)【点评】考查几何体的三视图的画法,从正面看的图形是主视图,从左面看到的图形是左
视图,从上面看到的图形是俯视图.
5.【分析】由于顺次连接四边各边中点得到的四边形是平行四边形,有对应边与原对角线平
行,由矩形的性质可知,应为对角线互相垂直的四边形.
【解答】解:由矩形的性质知,矩形的四角为直角,即每组邻边互相垂直,故原四边形的对
角线应互相垂直.
故选:C.
【点评】此题主要考查了矩形的判定定理(有一个角为直角的平行四边形为矩形),难度不
大.
6.【分析】证明∠ABE+∠ADE=180°,推出∠BAD+∠BED=180°即可解决问题.
【解答】解:∵∠ABC=∠ADE,∠ABC+∠ABE=180°,
∴∠ABE+∠ADE=180°,
∴∠BAD+∠BED=180°,
∵∠BAD= ,
∴∠BED=α180°﹣ .
故选:D. α
【点评】本题考查旋转的性质,解题的关键是理解题意,灵活运用所学知识解决问题,属于
中考常考题型.
7.【分析】当3为腰长时,将x=3代入原一元二次方程可求出k的值,将k值代入原方程可求
出方程的解,利用较小两边之和大于第三边可得出k=3符合题意;当3为底边长时,利用
等腰三角形的性质可得出根的判别式△=0,解之可得出k值,将k值代入原方程可求出
方程的解,利用较小两边之和大于第三边可得出k=4符合题意.
【解答】解:当3为腰长时,将x=3代入x2﹣4x+k=0,得:32﹣4×3+k=0,
解得:k=3,
当k=3时,原方程为x2﹣4x+3=0,
解得:x =1,x =3,
1 2
∵1+3=4,4>3,
∴k=3符合题意;
当3为底边长时,关于x的方程x2﹣4x+k=0有两个相等的实数根,
∴△=(﹣4)2﹣4×1×k=0,
解得:k=4,
第8页(共23页)当k=4时,原方程为x2﹣4x+4=0,
解得:x =x =2,
1 2
∵2+2=4,4>3,
∴k=4符合题意.
∴k的值为3或4.
故选:C.
【点评】本题考查了根的判别式、一元二次方程的解、等腰三角形的性质、三角形三边关系
以及根与系数的关系,分3为腰长及3为底边长两种情况,求出k值是解题的关键.
8.【分析】先由二次函数y=ax2+bx+c的图象得到字母系数的正负,再与一次函数y=acx+b
的图象相比较看是否一致.
【解答】解:A、由抛物线可知,a>0,b<0,c>0,则ac>0,由直线可知,ac>0,b>0,故本
选项错误;
B、由抛物线可知,a>0,b>0,c>0,则ac>0,由直线可知,ac>0,b>0,故本选项正确;
C、由抛物线可知,a<0,b>0,c>0,则ac<0,由直线可知,ac<0,b<0,故本选项错误;
D、由抛物线可知,a<0,b<0,c>0,则ac<0,由直线可知,ac>0,b>0,故本选项错误.
故选:B.
【点评】本题考查二次函数和一次函数的图象,解题的关键是明确一次函数和二次函数性
质.
二、填空题(本大题共6个小题,每小题3分,共18分,只要求把最后结果填写在答题卡的相
应区域内.)
9.【分析】直接利用二次根式的混合运算法则计算得出答案.
【解答】解:原式=( )2﹣42
=3﹣16
=﹣13.
故答案为:﹣13.
【点评】此题主要考查了二次根式的混合运算,正确运用乘法公式是解题关键.
10.【分析】分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得
到分式方程的解.
【解答】解:方程 = ,
去分母得:(x﹣1)2=x(x+1),
第9页(共23页)整理得:x2﹣2x+1=x2+x,
解得:x= ,
经检验x= 是分式方程的解.
故答案为:x= .
【点评】此题考查了解分式方程,利用了转化的思想,解分式方程注意要检验.
11.【分析】过点D作DE⊥BC,由平行线平分线段定理可得E是BC的中点,再根据三角函数
的意义,可求出答案.
【解答】解:过点D作DE⊥BC,垂足为E,
∵∠ACB=90°,DE⊥BC,
∴DE∥AC,
又∵点D为AB边的中点,
∴BE=EC= BC=2,
在Rt△DCE中,cos∠DCB= = ,
故答案为: .
【点评】考查直角三角形的边角关系,理解直角三角形的边角关系是得出正确答案的前提,
作高构造直角三角形是常用的方法.
12.【分析】首先根据题意画出树状图,然后由树状图求得所有等可能的结果,然后利用概率
公式求解即可求得答案.
【解答】解:画树状图得:
第10页(共23页)则共有12种等可能的结果,
∵反比例函数y= 中,图象在二、四象限,
∴ab<0,
∴有8种符合条件的结果,
∴P(图象在二、四象限)= = ,
故答案为: .
【点评】本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不
遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以
上完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.
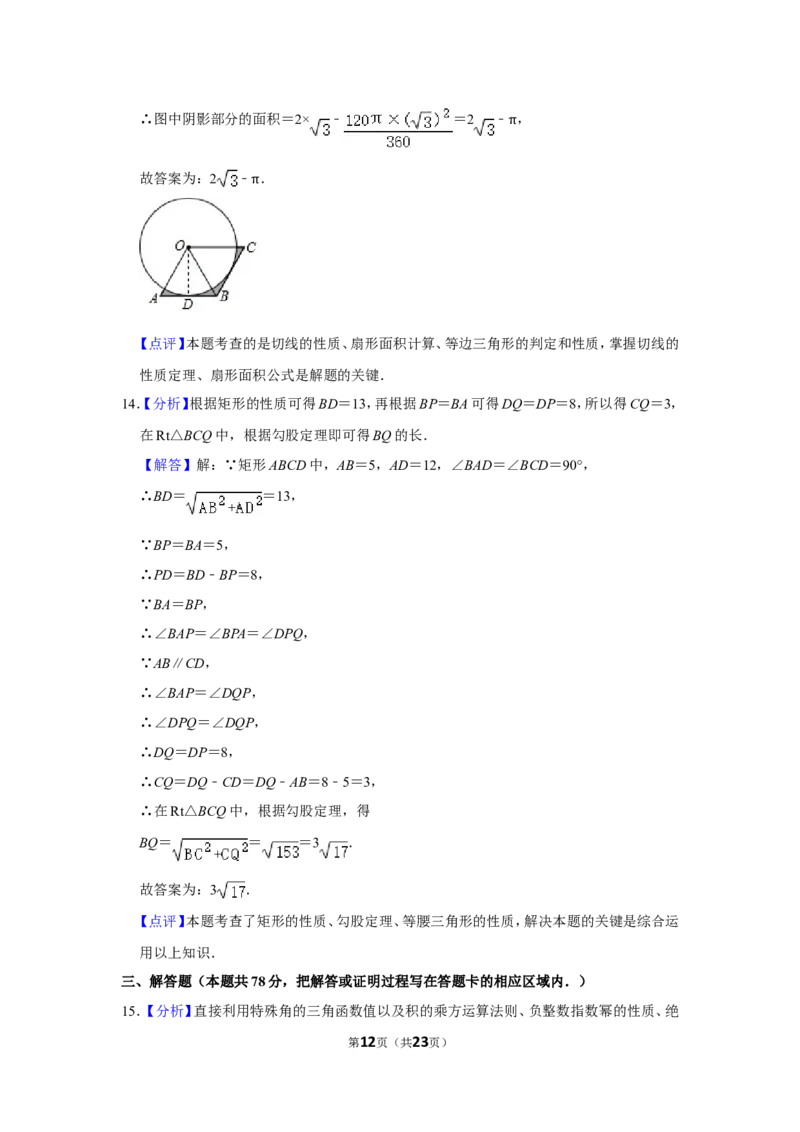
13.【分析】连接OD,根据菱形的性质得到OA=AB,得到△OAB为等边三角形,根据切线的
性质得到OD⊥AB,根据余弦的定义求出OD,根据菱形面积公式、扇形面积公式计算,得
到答案.
【解答】解:连接OD,
∵四边形OABC为菱形,
∴OA=AB,
∵OA=OB,
∴OA=OB=AB,
∴△OAB为等边三角形,
∴∠A=∠AOB=60°,
∵AB是 O的切线,
∴OD⊥⊙AB,
∴OD=OA•sinA= ,
同理可知,△OBC为等边三角形,
∴∠BOC=60°,
第11页(共23页)∴图中阴影部分的面积=2× ﹣ =2 ﹣ ,
π
故答案为:2 ﹣ .
π
【点评】本题考查的是切线的性质、扇形面积计算、等边三角形的判定和性质,掌握切线的
性质定理、扇形面积公式是解题的关键.
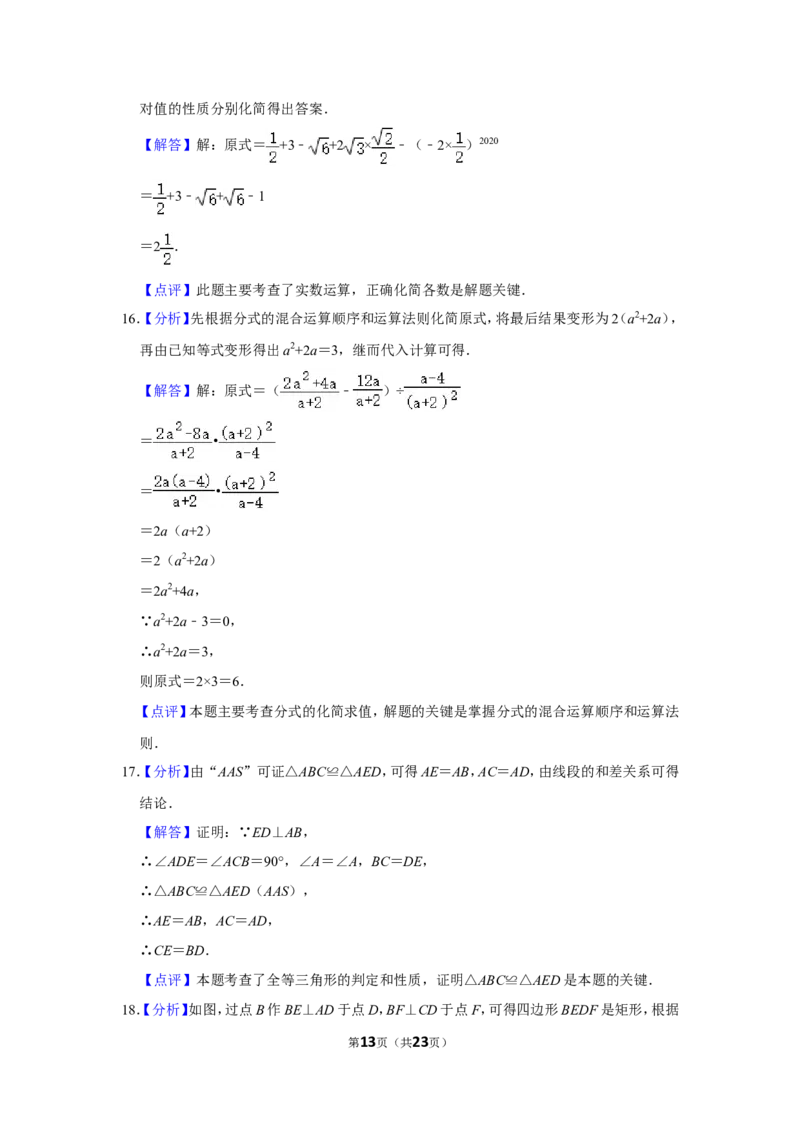
14.【分析】根据矩形的性质可得BD=13,再根据BP=BA可得DQ=DP=8,所以得CQ=3,
在Rt△BCQ中,根据勾股定理即可得BQ的长.
【解答】解:∵矩形ABCD中,AB=5,AD=12,∠BAD=∠BCD=90°,
∴BD= =13,
∵BP=BA=5,
∴PD=BD﹣BP=8,
∵BA=BP,
∴∠BAP=∠BPA=∠DPQ,
∵AB∥CD,
∴∠BAP=∠DQP,
∴∠DPQ=∠DQP,
∴DQ=DP=8,
∴CQ=DQ﹣CD=DQ﹣AB=8﹣5=3,
∴在Rt△BCQ中,根据勾股定理,得
BQ= = =3 .
故答案为:3 .
【点评】本题考查了矩形的性质、勾股定理、等腰三角形的性质,解决本题的关键是综合运
用以上知识.
三、解答题(本题共78分,把解答或证明过程写在答题卡的相应区域内.)
15.【分析】直接利用特殊角的三角函数值以及积的乘方运算法则、负整数指数幂的性质、绝
第12页(共23页)对值的性质分别化简得出答案.
【解答】解:原式= +3﹣ +2 × ﹣(﹣2× )2020
= +3﹣ + ﹣1
=2 .
【点评】此题主要考查了实数运算,正确化简各数是解题关键.
16.【分析】先根据分式的混合运算顺序和运算法则化简原式,将最后结果变形为2(a2+2a),
再由已知等式变形得出a2+2a=3,继而代入计算可得.
【解答】解:原式=( ﹣ )÷
= •
= •
=2a(a+2)
=2(a2+2a)
=2a2+4a,
∵a2+2a﹣3=0,
∴a2+2a=3,
则原式=2×3=6.
【点评】本题主要考查分式的化简求值,解题的关键是掌握分式的混合运算顺序和运算法
则.
17.【分析】由“AAS”可证△ABC≌△AED,可得AE=AB,AC=AD,由线段的和差关系可得
结论.
【解答】证明:∵ED⊥AB,
∴∠ADE=∠ACB=90°,∠A=∠A,BC=DE,
∴△ABC≌△AED(AAS),
∴AE=AB,AC=AD,
∴CE=BD.
【点评】本题考查了全等三角形的判定和性质,证明△ABC≌△AED是本题的关键.
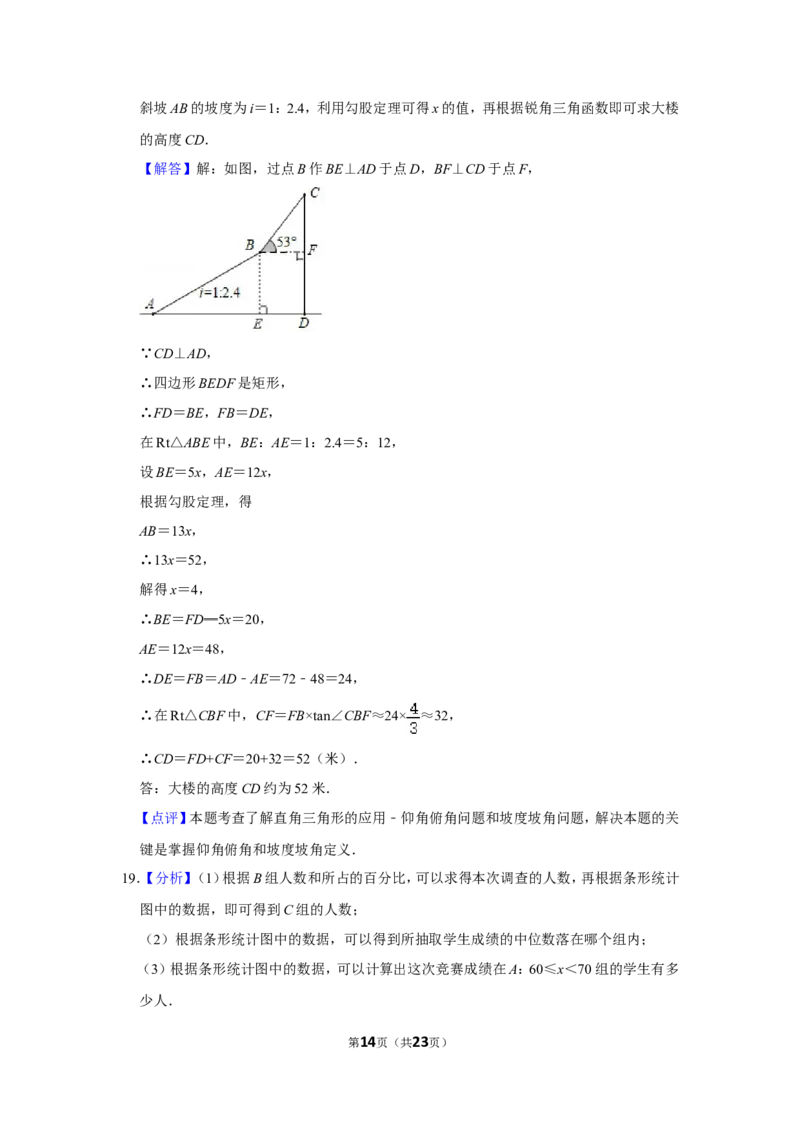
18.【分析】如图,过点B作BE⊥AD于点D,BF⊥CD于点F,可得四边形BEDF是矩形,根据
第13页(共23页)斜坡AB的坡度为i=1:2.4,利用勾股定理可得x的值,再根据锐角三角函数即可求大楼
的高度CD.
【解答】解:如图,过点B作BE⊥AD于点D,BF⊥CD于点F,
∵CD⊥AD,
∴四边形BEDF是矩形,
∴FD=BE,FB=DE,
在Rt△ABE中,BE:AE=1:2.4=5:12,
设BE=5x,AE=12x,
根据勾股定理,得
AB=13x,
∴13x=52,
解得x=4,
∴BE=FD═5x=20,
AE=12x=48,
∴DE=FB=AD﹣AE=72﹣48=24,
∴在Rt△CBF中,CF=FB×tan∠CBF≈24× ≈32,
∴CD=FD+CF=20+32=52(米).
答:大楼的高度CD约为52米.
【点评】本题考查了解直角三角形的应用﹣仰角俯角问题和坡度坡角问题,解决本题的关
键是掌握仰角俯角和坡度坡角定义.
19.【分析】(1)根据B组人数和所占的百分比,可以求得本次调查的人数,再根据条形统计
图中的数据,即可得到C组的人数;
(2)根据条形统计图中的数据,可以得到所抽取学生成绩的中位数落在哪个组内;
(3)根据条形统计图中的数据,可以计算出这次竞赛成绩在A:60≤x<70组的学生有多
少人.
第14页(共23页)【解答】解:(1)本次抽取的学生有:12÷20%=60(人),
C组学生有:60﹣6﹣12﹣18=24(人),
即被抽取的学生成绩在C:80≤x<90组的有24人;
(2)所抽取学生成绩的中位数落在C:80≤x<90这一组内;
(3)1500× =150(人),
答:这次竞赛成绩在A:60≤x<70组的学生有150人.
【点评】本题考查条形统计图、扇形统计图、用样本估计总体、中位数,解答本题的关键是
明确题意,利用数形结合的思想解答.
20.【分析】(1)先根据点A坐标求出反比例函数解析式,再求出点B的坐标,继而根据点A、
B坐标可得直线解析式;
(2)先根据直线解析式求出点C的坐标,再设P(n,0),知PC=|﹣1﹣n|,根据S△ACP =
•PC•y =4求出n的值即可得出答案.
A
【解答】解:(1)将点A(1,2)代入y= ,得:m=2,
∴y= ,
当y=﹣1时,x=﹣2,
∴B(﹣2,﹣1),
将A(1,2)、B(﹣2,﹣1)代入y=kx+b,
得: ,
解得 ,
∴y=x+1;
∴一次函数解析式为y=x+1,反比例函数解析式为y= ;
(2)在y=x+1中,当y=0时,x+1=0,
解得x=﹣1,
∴C(﹣1,0),
设P(n,0),
第15页(共23页)则PC=|﹣1﹣n|,
∵S△ACP = •PC•y
A
=4,
∴ ×|﹣1﹣n|×2=4,
解得n=3或n=﹣5,
∴点P的坐标为(3,0)或(﹣5,0).
【点评】本题主要考查反比例函数与一次函数的交点问题,解题的关键是掌握待定系数法
求函数解析式及两点间的距离公式、三角形的面积问题.
21.【分析】(1)设购买一根跳绳需要x元,购买一个毽子需要y元,根据“购买2根跳绳和5
个毽子共需32元;购买4根跳绳和3个毽子共需36元”,即可得出关于x,y的二元一次
方程组,解之即可得出结论;
(2)设购买m根跳绳,则购买(54﹣m)个毽子,根据购买的总费用不能超过260元且购买
跳绳的数量多于20根,即可得出关于m的一元一次不等式组,解之即可得出m的取值范
围,结合m为正整数即可得出各购买方案.
【解答】解:(1)设购买一根跳绳需要x元,购买一个毽子需要y元,
依题意,得: ,
解得: .
答:购买一根跳绳需要6元,购买一个毽子需要4元.
(2)设购买m根跳绳,则购买(54﹣m)个毽子,
依题意,得: ,
解得:20<m≤22.
又∵m为正整数,
∴m可以为21,22.
∴共有2种购买方案,方案1:购买21根跳绳,33个毽子;方案2:购买22根跳绳,32个毽
子.
【点评】本题考查了二元一次方程组的应用以及一元一次不等式组的应用,解题的关键是:
(1)找准等量关系,正确列出二元一次方程组;(2)根据各数量之间的关系,正确列出一元
一次不等式组.
第16页(共23页)22.【分析】(1)连接AD、OD.先证明∠ADB=90°,∠EDO=90°,从而可证明∠EDA=
∠ODB,由OD=OB可得到∠EDA=∠OBD,由等腰三角形的性质可知∠CAD=∠BAD,
故此∠EAD+∠EDA=90°,由三角形的内角和定理可知∠DEA=90°,于是可得到
DE⊥AC.
(2)由等腰三角形的性质求出BD=CD=8,由勾股定理求出AD的长,根据三角形的面积
得出答案.
【解答】(1)证明:连接AD、OD.
∵AB是圆O的直径,
∴∠ADB=90°.
∴∠ADO+∠ODB=90°.
∵DE是圆O的切线,
∴OD⊥DE.
∴∠EDA+∠ADO=90°.
∴∠EDA=∠ODB.
∵OD=OB,
∴∠ODB=∠OBD.
∴∠EDA=∠OBD.
∵AC=AB,AD⊥BC,
∴∠CAD=∠BAD.
∵∠DBA+∠DAB=90°,
∴∠EAD+∠EDA=90°.
∴∠DEA=90°.
∴DE⊥AC.
(2)解:∵∠ADB=90°,AB=AC,
∴BD=CD,
∵ O的半径为5,BC=16,
∴⊙AC=10,CD=8,
第17页(共23页)∴AD= =6,
∵S△ADC = AC•DE,
∴DE= = = .
【点评】本题考查了圆周角定理,切线的性质,等腰三角形的性质和判定,三角形的内角和
定理,勾股定理,三角形的面积等知识,掌握切线的性质是解题的关键.
23.【分析】(1)证明△AOE≌△COD(AAS),由全等三角形的性质得出CD=AE,OD=OE,
则可得出结论;
(2) 过点A作AE∥DC交BD于点E,由(1)得出∠ABE=∠AEB,由折叠的性质可得出
∠AB①D'=∠BAE,则BD'∥AE,可得出结论;
过点A作AE∥DC交BD于点E,延长AE交BC于点F,证明△AED∽△BEF,得出
②
,证明△BEF∽△BDC,由相似三角形的性质得出 = ,根据AE=CD,DE=
2OD可得出结论.
【解答】(1)证明:∵AE∥DC,
∴∠CDO=∠AEO,∠EAO=∠DCO,
又∵OA=OC,
∴△AOE≌△COD(AAS),
∴CD=AE,OD=OE,
∵OB=OE+BE,OB=OD+CD,
∴BE=CD,
∴AE=BE;
(2) 证明:如图1,过点A作AE∥DC交BD于点E,
①
由(1)可知△AOE≌△COD,AE=BE,
∴∠ABE=∠AEB,
第18页(共23页)∵将△ABD沿AB翻折得到△ABD',
∴∠ABD'=∠ABD,
∴∠ABD'=∠BAE,
∴BD'∥AE,
又∵AE∥CD
∴BD'∥CD.
证明:如图2,过点A作AE∥DC交BD于点E,延长AE交BC于点F,
②
∵AD'∥BC,BD'∥AE,
∴四边形AD'BF为平行四边形.
∴∠D'=∠AFB,
∵将△ABD沿AB翻折得到△ABD'.
∴∠D'=∠ADB,
∴∠AFB=∠ADB,
又∵∠AED=∠BEF,
∴△AED∽△BEF,
∴ ,
∵AE=CD,
∴ ,
∵EF∥CD,
∴△BEF∽△BDC,
∴ = ,
∴ ,
∴CD2=DE•BD,
第19页(共23页)∵△AOE≌△COD,
∴OD=OE,
∴DE=2OD,
∴CD2=2OD•BD.
【点评】本题是相似形综合题,考查了翻折的性质,全等三角形的判定与性质,相似三角形
的判定与性质,平行线的判定与性质,等腰三角形的判定与性质,熟练掌握相似三角形的
判定与性质是解题的关键.
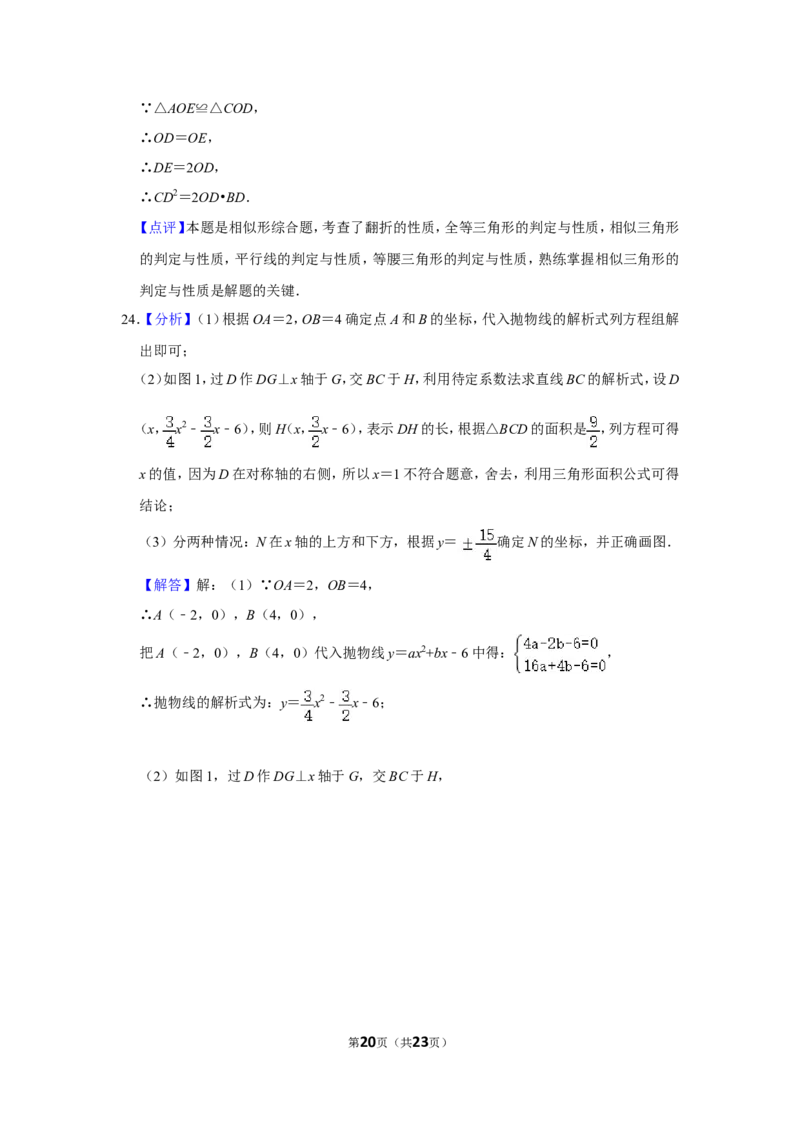
24.【分析】(1)根据OA=2,OB=4确定点A和B的坐标,代入抛物线的解析式列方程组解
出即可;
(2)如图1,过D作DG⊥x轴于G,交BC于H,利用待定系数法求直线BC的解析式,设D
(x, x2﹣ x﹣6),则H(x, x﹣6),表示DH的长,根据△BCD的面积是 ,列方程可得
x的值,因为D在对称轴的右侧,所以x=1不符合题意,舍去,利用三角形面积公式可得
结论;
(3)分两种情况:N在x轴的上方和下方,根据y= 确定N的坐标,并正确画图.
【解答】解:(1)∵OA=2,OB=4,
∴A(﹣2,0),B(4,0),
把A(﹣2,0),B(4,0)代入抛物线y=ax2+bx﹣6中得: ,
∴抛物线的解析式为:y= x2﹣ x﹣6;
(2)如图1,过D作DG⊥x轴于G,交BC于H,
第20页(共23页)当x=0时,y=﹣6,
∴C(0,﹣6),
设BC的解析式为:y=kx+b,
则 ,解得: ,
∴BC的解析式为:y= x﹣6,
设D(x, x2﹣ x﹣6),则H(x, x﹣6),
∴DH= x﹣6﹣( x2﹣ x﹣6)=﹣ ,
∵△BCD的面积是 ,
∴ ,
∴ ,
解得:x=1或3,
∵点D在直线l右侧的抛物线上,
∴D(3,﹣ ),
∴△ABD的面积= = = ;
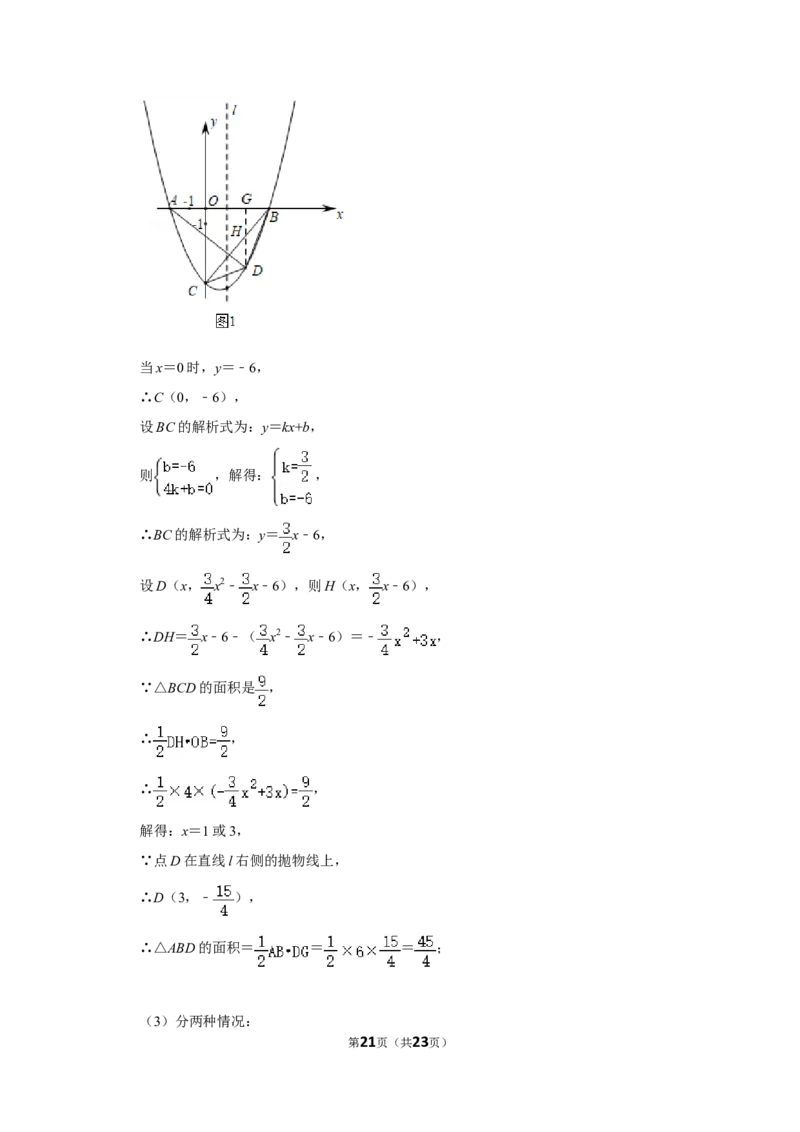
(3)分两种情况:
第21页(共23页)如图2,N在x轴的上方时,四边形MNBD是平行四边形,
①
∵B(4,0),D(3,﹣ ),且M在x轴上,
∴N的纵坐标为 ,
当y= 时,即 x2﹣ x﹣6= ,
解得:x=1+ 或1﹣ ,
∴N(1﹣ , )或(1+ , );
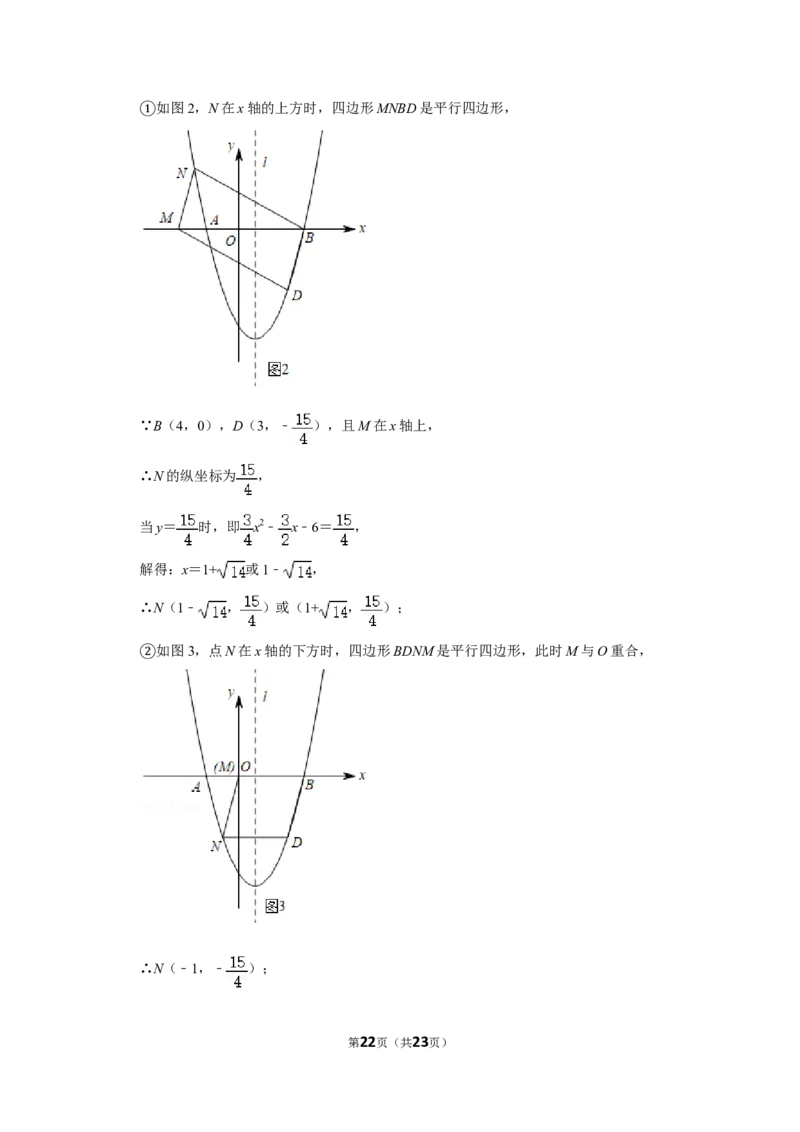
如图3,点N在x轴的下方时,四边形BDNM是平行四边形,此时M与O重合,
②
∴N(﹣1,﹣ );
第22页(共23页)综上,点N的坐标为:(1﹣ , )或(1+ , )或(﹣1,﹣ ).
【点评】此题主要考查二次函数的综合问题,会求函数与坐标轴的交点,会利用待定系数
法求函数解析式,会利用数形结合的思想解决平行四边形的问题,并结合方程思想解决问
题.
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布
日期:2020/8/12 15:51:02;用户:18366185883;邮箱:18366185883;学号:22597006
第23页(共23页)