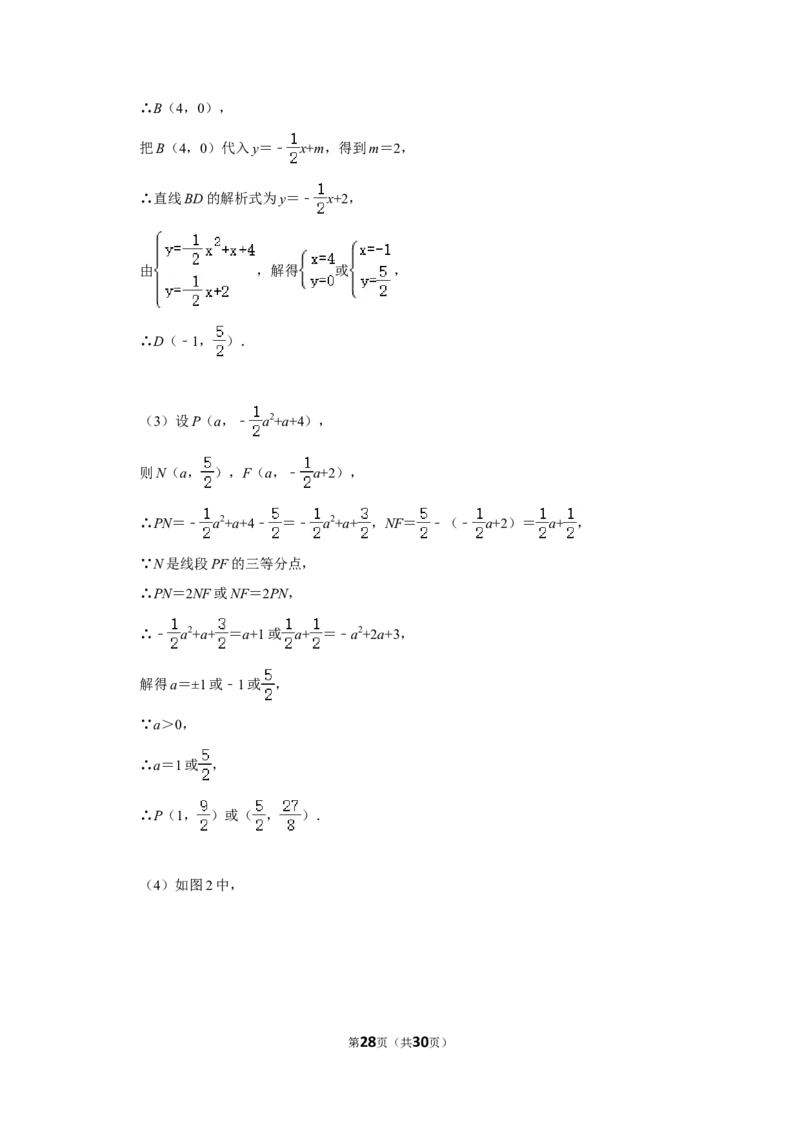文档内容
2020年辽宁省丹东市中考数学试卷
一、选择题(下列各题的备选答案中,只有一个是正确的.每小题3分,共24分)
1.(3分)﹣5的绝对值等于( )
A.﹣5 B.5 C.﹣ D.
2.(3分)下面计算正确的是( )
A.a3•a3=2a3 B.2a2+a2=3a4
C.a9÷a3=a3 D.(﹣3a2)3=﹣27a6
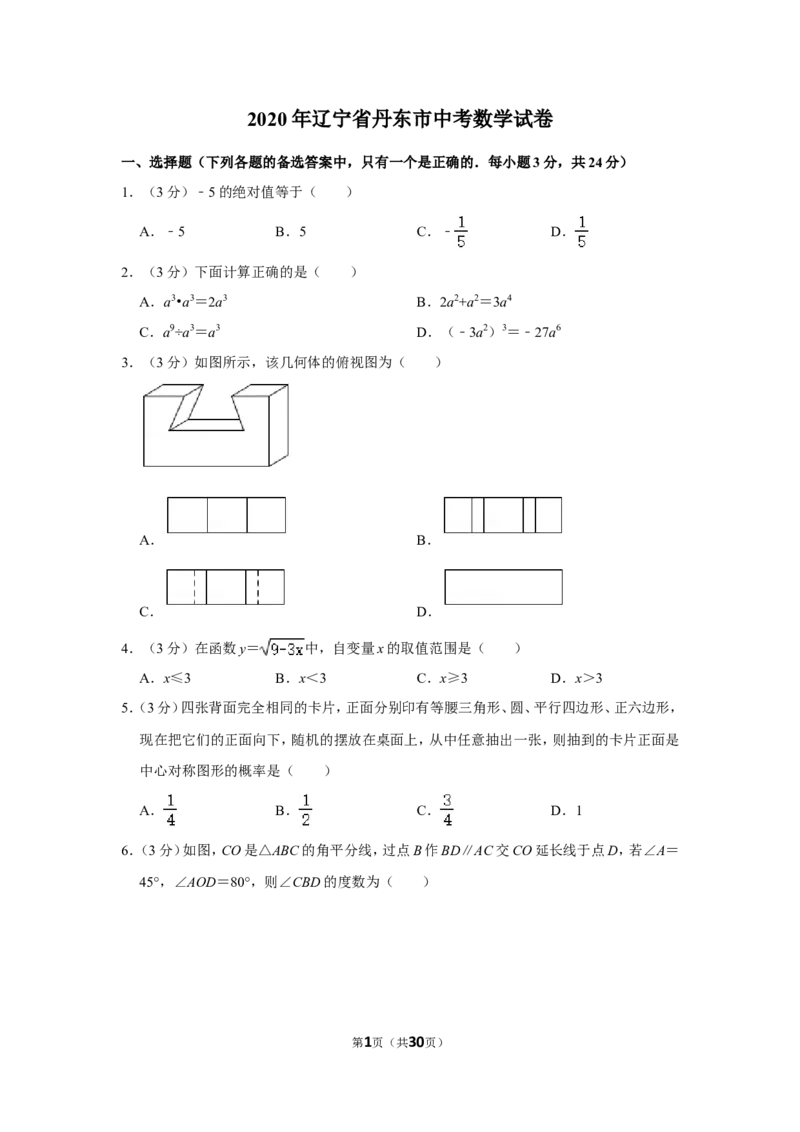
3.(3分)如图所示,该几何体的俯视图为( )
A. B.
C. D.
4.(3分)在函数y= 中,自变量x的取值范围是( )
A.x≤3 B.x<3 C.x≥3 D.x>3
5.(3分)四张背面完全相同的卡片,正面分别印有等腰三角形、圆、平行四边形、正六边形,
现在把它们的正面向下,随机的摆放在桌面上,从中任意抽出一张,则抽到的卡片正面是
中心对称图形的概率是( )
A. B. C. D.1
6.(3分)如图,CO是△ABC的角平分线,过点B作BD∥AC交CO延长线于点D,若∠A=
45°,∠AOD=80°,则∠CBD的度数为( )
第1页(共30页)A.100° B.110° C.125° D.135°
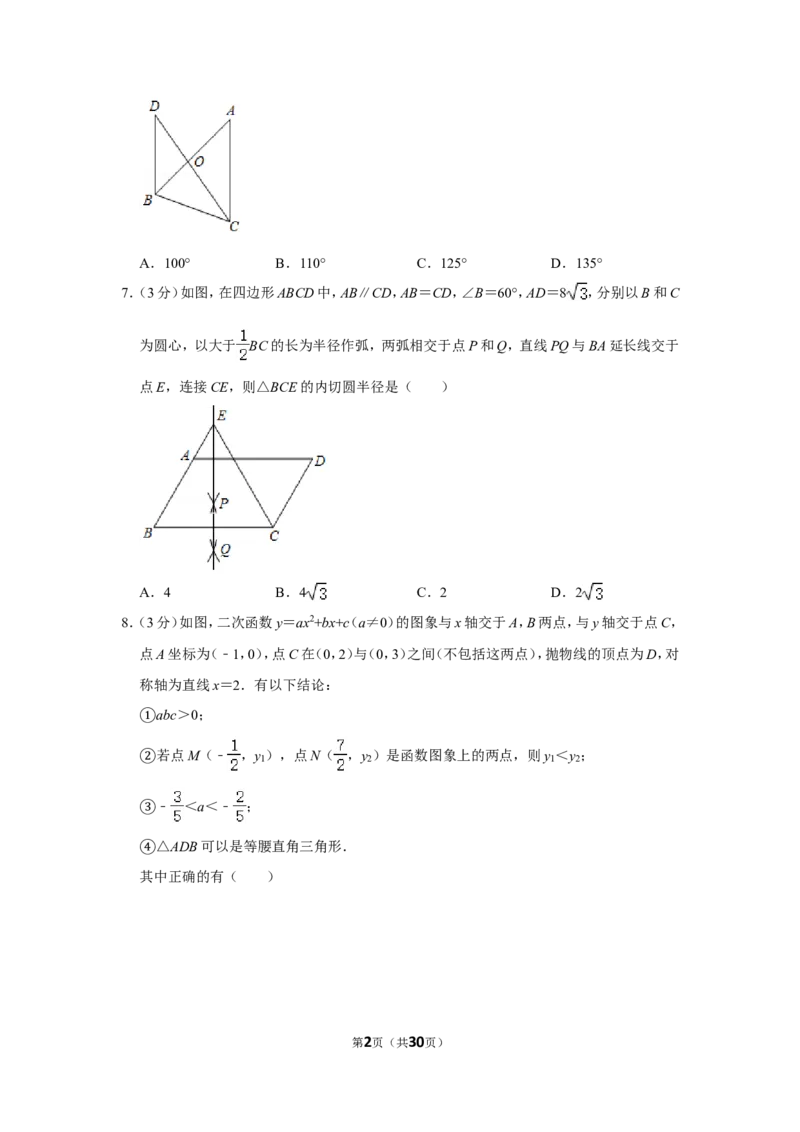
7.(3分)如图,在四边形ABCD中,AB∥CD,AB=CD,∠B=60°,AD=8 ,分别以B和C
为圆心,以大于 BC的长为半径作弧,两弧相交于点P和Q,直线PQ与BA延长线交于
点E,连接CE,则△BCE的内切圆半径是( )
A.4 B.4 C.2 D.2
8.(3分)如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,
点A坐标为(﹣1,0),点C在(0,2)与(0,3)之间(不包括这两点),抛物线的顶点为D,对
称轴为直线x=2.有以下结论:
abc>0;
①
若点M(﹣ ,y ),点N( ,y )是函数图象上的两点,则y <y ;
1 2 1 2
②
﹣ <a<﹣ ;
③
△ADB可以是等腰直角三角形.
④其中正确的有( )
第2页(共30页)A.1个 B.2个 C.3个 D.4个
二、填空题(每小题3分,共24分)
9.(3分)据有关报道,2020年某市斥资约5800000元改造老旧小区,数据5800000用科学记
数法表示为 .
10.(3分)因式分解:mn3﹣4mn= .
11.(3分)一次函数y=﹣2x+b,且b>0,则它的图象不经过第 象限.
12.(3分)甲、乙两人进行飞镖比赛,每人投5次,所得平均环数相等,其中甲所得环数的方
差为5,乙所得环数如下:2,3,5,7,8,那么成绩较稳定的是 (填“甲”或“乙”).
13.(3分)关于x的方程(m+1)x2+3x﹣1=0有两个实数根,则m的取值范围是 .
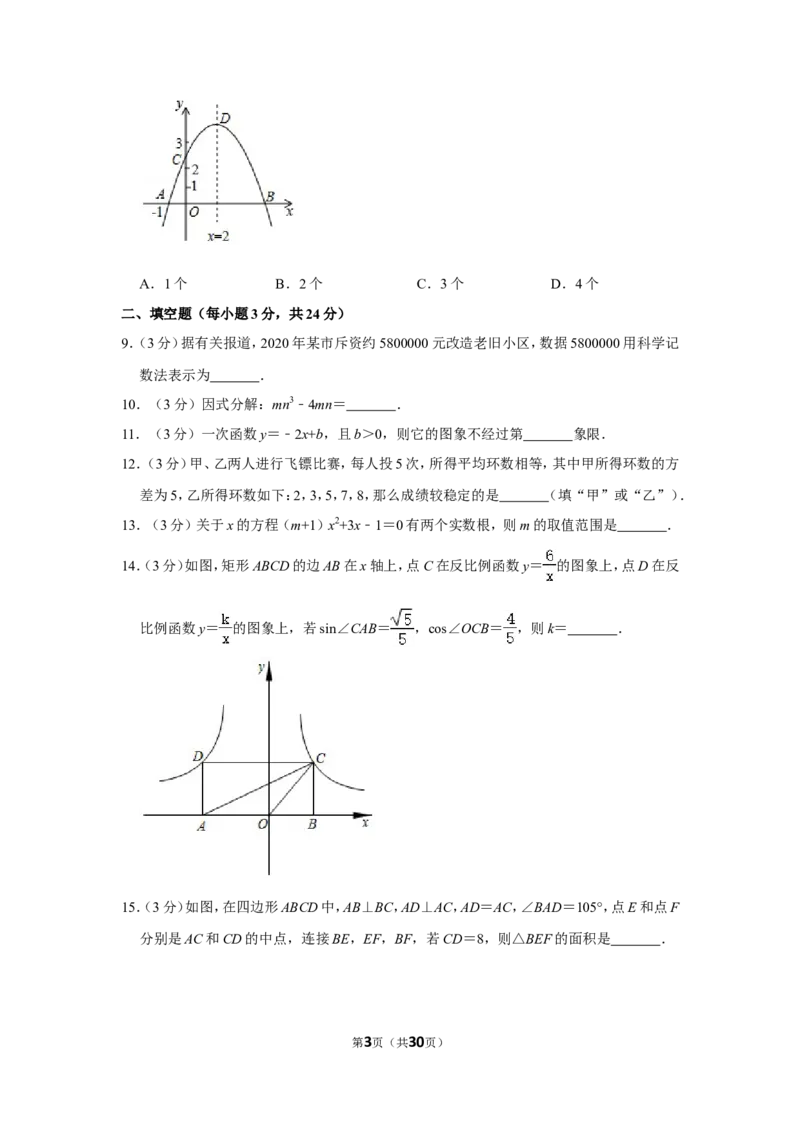
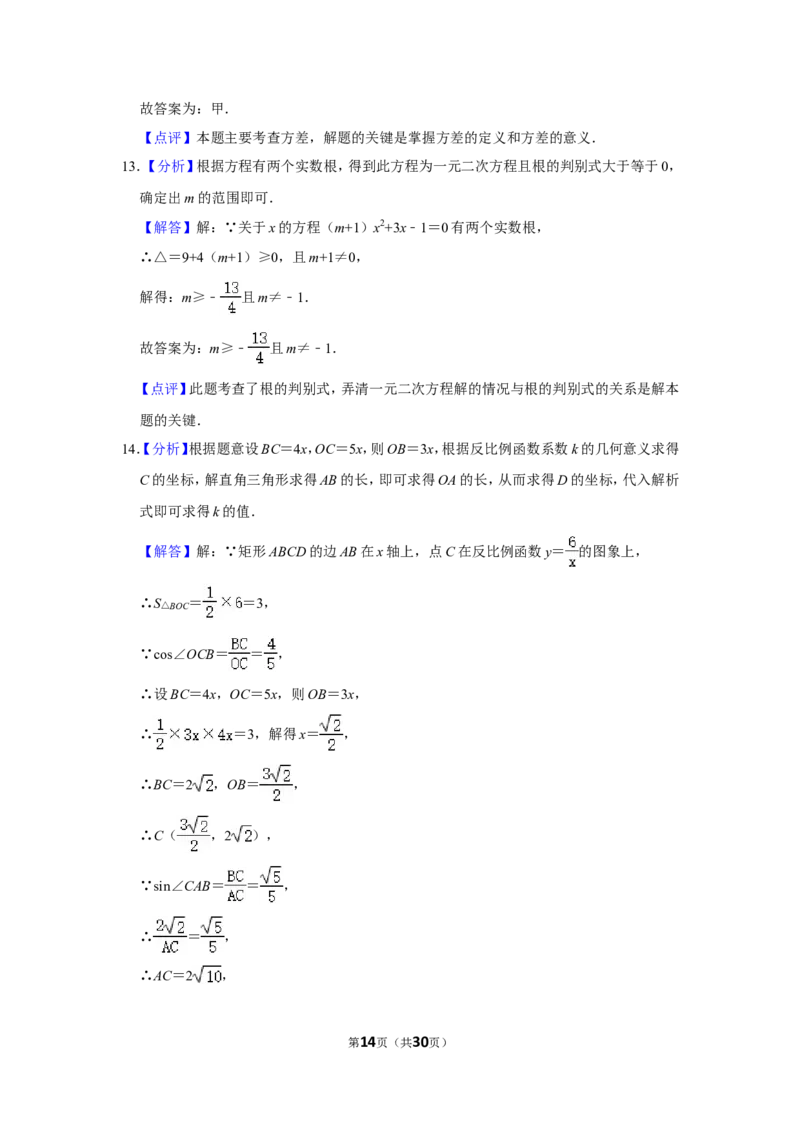
14.(3分)如图,矩形ABCD的边AB在x轴上,点C在反比例函数y= 的图象上,点D在反
比例函数y= 的图象上,若sin∠CAB= ,cos∠OCB= ,则k= .
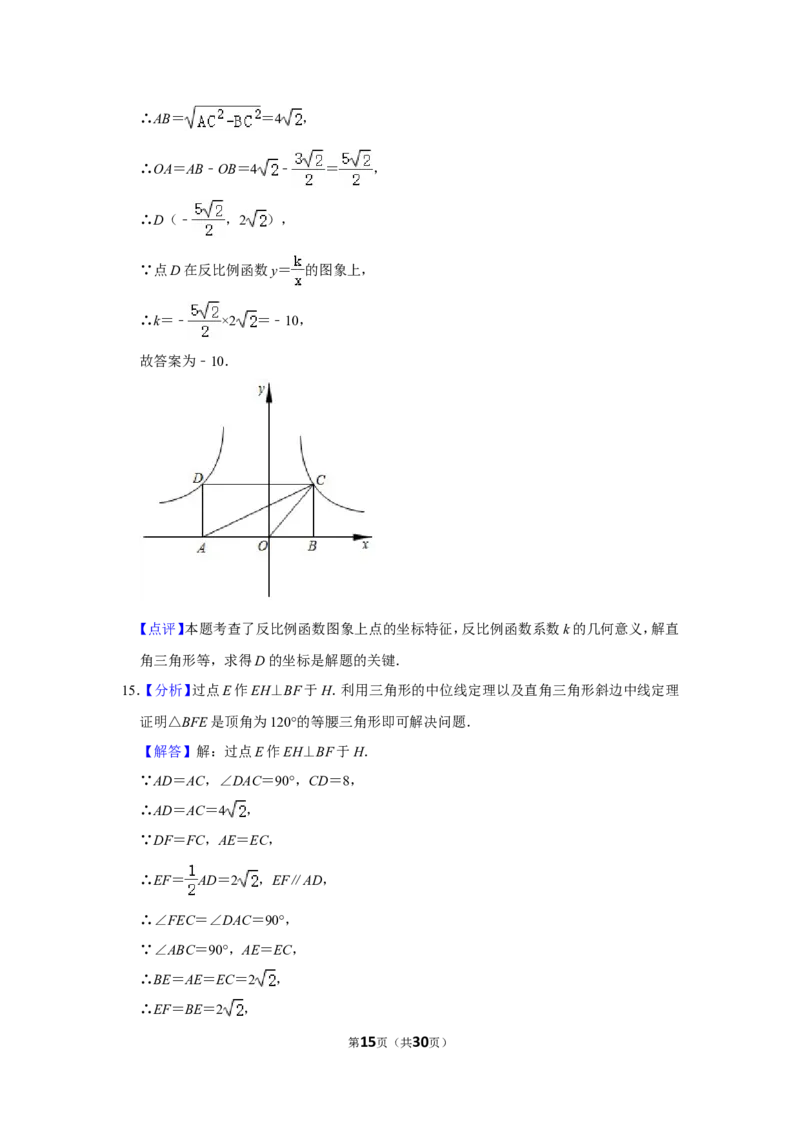
15.(3分)如图,在四边形ABCD中,AB⊥BC,AD⊥AC,AD=AC,∠BAD=105°,点E和点F
分别是AC和CD的中点,连接BE,EF,BF,若CD=8,则△BEF的面积是 .
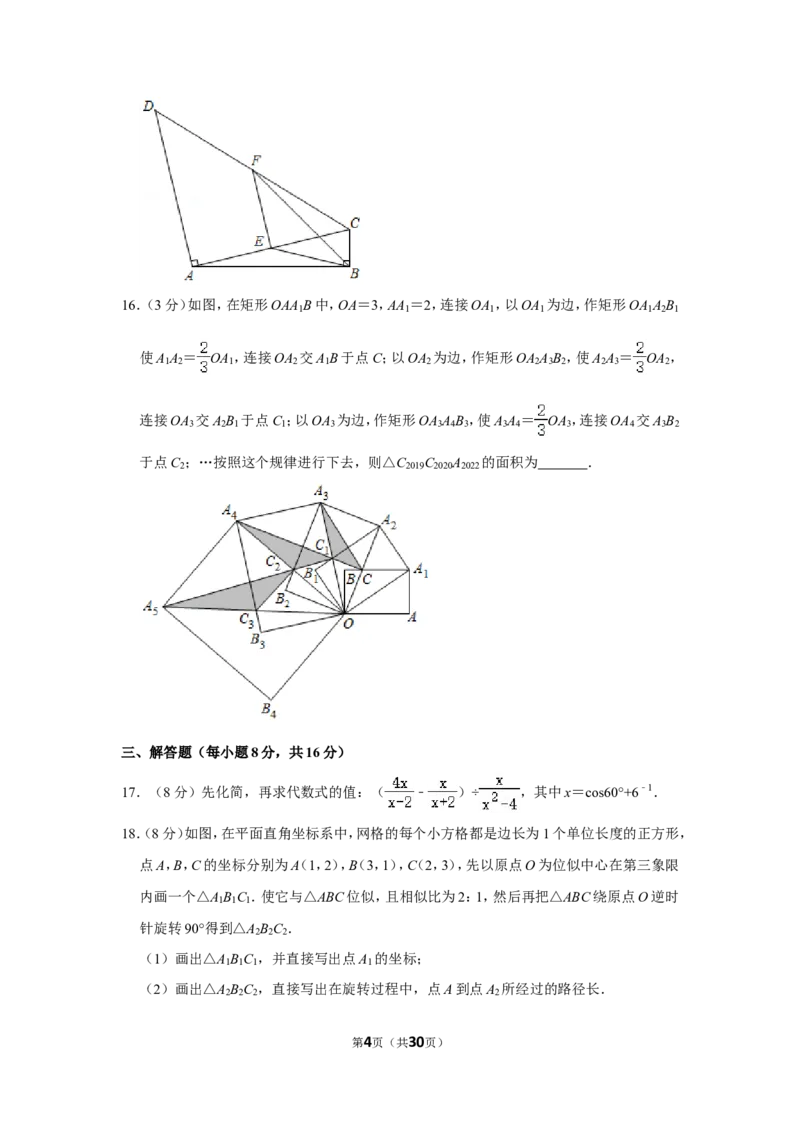
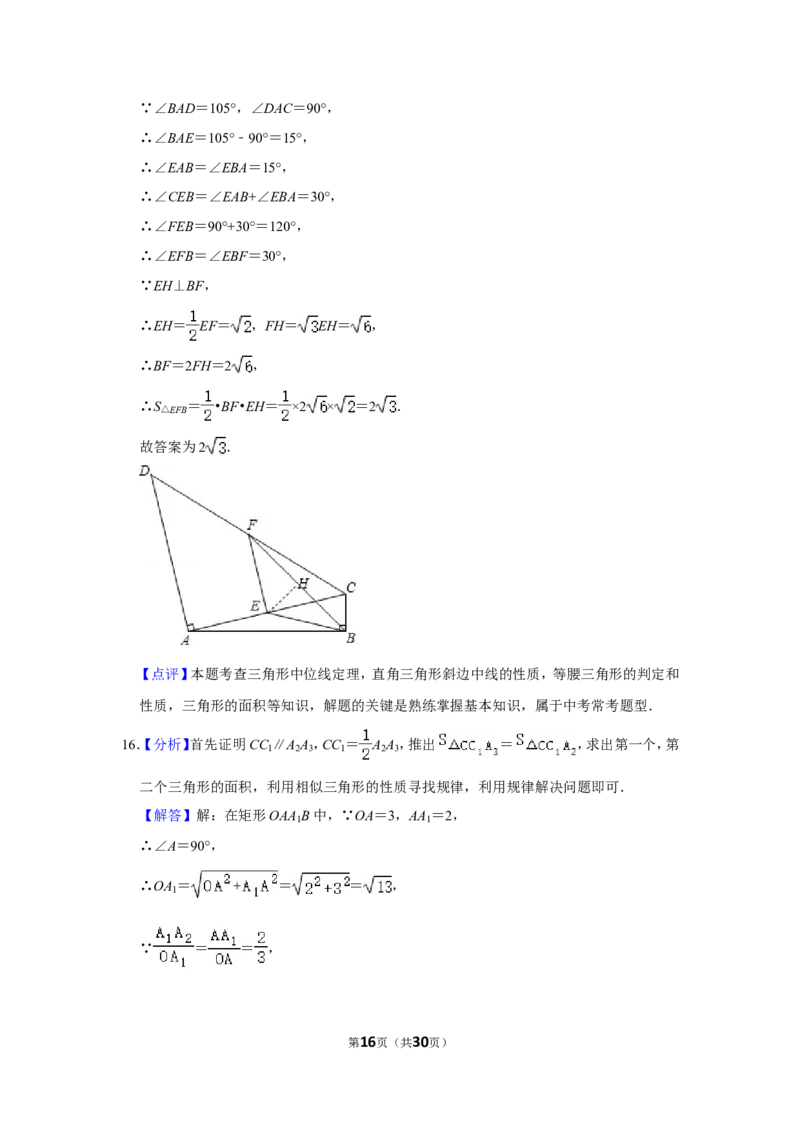
第3页(共30页)16.(3分)如图,在矩形OAA B中,OA=3,AA =2,连接OA ,以OA 为边,作矩形OA A B
1 1 1 1 1 2 1
使A A = OA ,连接OA 交A B于点C;以OA 为边,作矩形OA A B ,使A A = OA ,
1 2 1 2 1 2 2 3 2 2 3 2
连接OA 交A B 于点C ;以OA 为边,作矩形OA A B ,使A A = OA ,连接OA 交A B
3 2 1 1 3 3 4 3 3 4 3 4 3 2
于点C ;…按照这个规律进行下去,则△C C A 的面积为 .
2 2019 2020 2022
三、解答题(每小题8分,共16分)
17.(8分)先化简,再求代数式的值:( ﹣ )÷ ,其中x=cos60°+6﹣1.
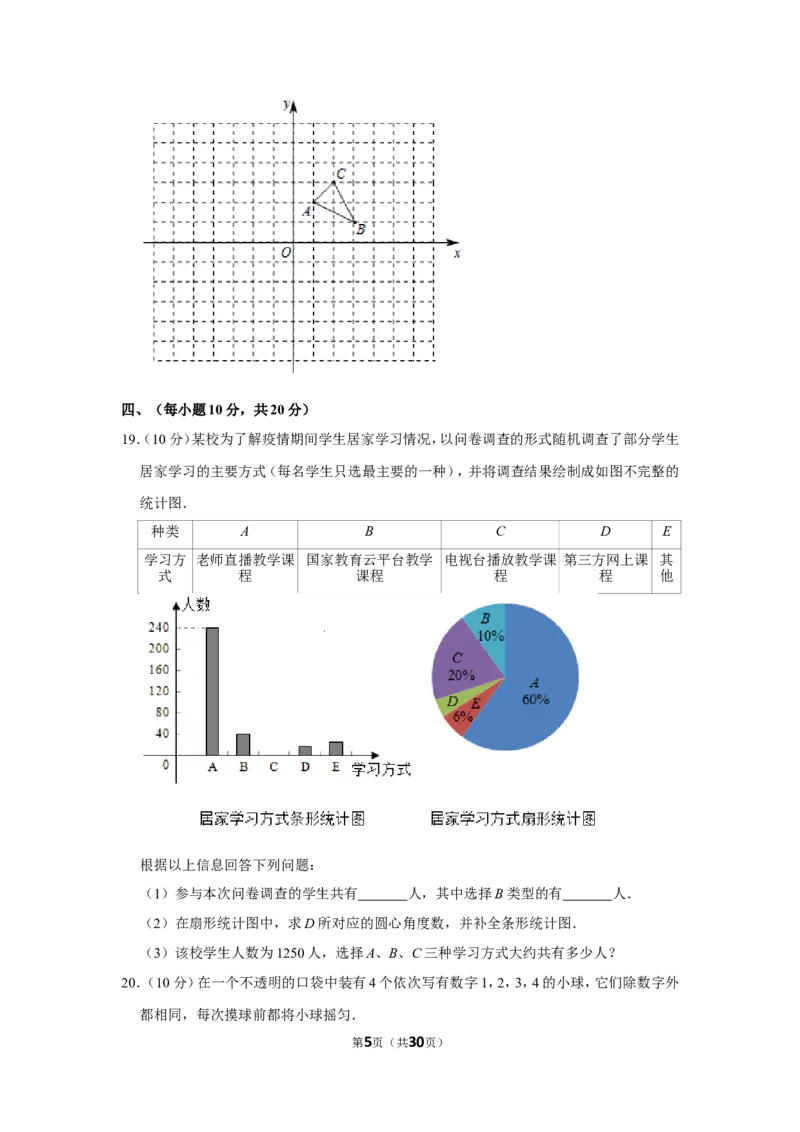
18.(8分)如图,在平面直角坐标系中,网格的每个小方格都是边长为1个单位长度的正方形,
点A,B,C的坐标分别为A(1,2),B(3,1),C(2,3),先以原点O为位似中心在第三象限
内画一个△A B C .使它与△ABC位似,且相似比为2:1,然后再把△ABC绕原点O逆时
1 1 1
针旋转90°得到△A B C .
2 2 2
(1)画出△A B C ,并直接写出点A 的坐标;
1 1 1 1
(2)画出△A B C ,直接写出在旋转过程中,点A到点A 所经过的路径长.
2 2 2 2
第4页(共30页)四、(每小题10分,共20分)
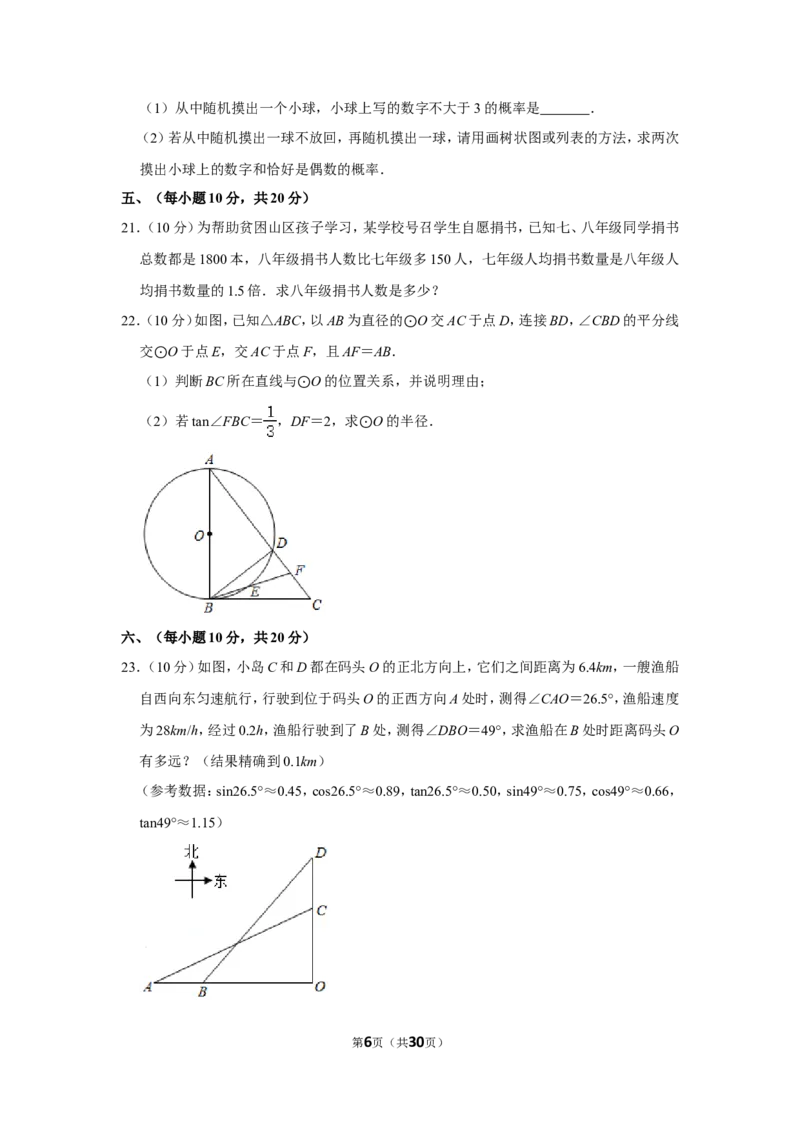
19.(10分)某校为了解疫情期间学生居家学习情况,以问卷调查的形式随机调查了部分学生
居家学习的主要方式(每名学生只选最主要的一种),并将调查结果绘制成如图不完整的
统计图.
种类 A B C D E
学习方 老师直播教学课 国家教育云平台教学 电视台播放教学课 第三方网上课 其
式 程 课程 程 程 他
根据以上信息回答下列问题:
(1)参与本次问卷调查的学生共有 人,其中选择B类型的有 人.
(2)在扇形统计图中,求D所对应的圆心角度数,并补全条形统计图.
(3)该校学生人数为1250人,选择A、B、C三种学习方式大约共有多少人?
20.(10分)在一个不透明的口袋中装有4个依次写有数字1,2,3,4的小球,它们除数字外
都相同,每次摸球前都将小球摇匀.
第5页(共30页)(1)从中随机摸出一个小球,小球上写的数字不大于3的概率是 .
(2)若从中随机摸出一球不放回,再随机摸出一球,请用画树状图或列表的方法,求两次
摸出小球上的数字和恰好是偶数的概率.
五、(每小题10分,共20分)
21.(10分)为帮助贫困山区孩子学习,某学校号召学生自愿捐书,已知七、八年级同学捐书
总数都是1800本,八年级捐书人数比七年级多150人,七年级人均捐书数量是八年级人
均捐书数量的1.5倍.求八年级捐书人数是多少?
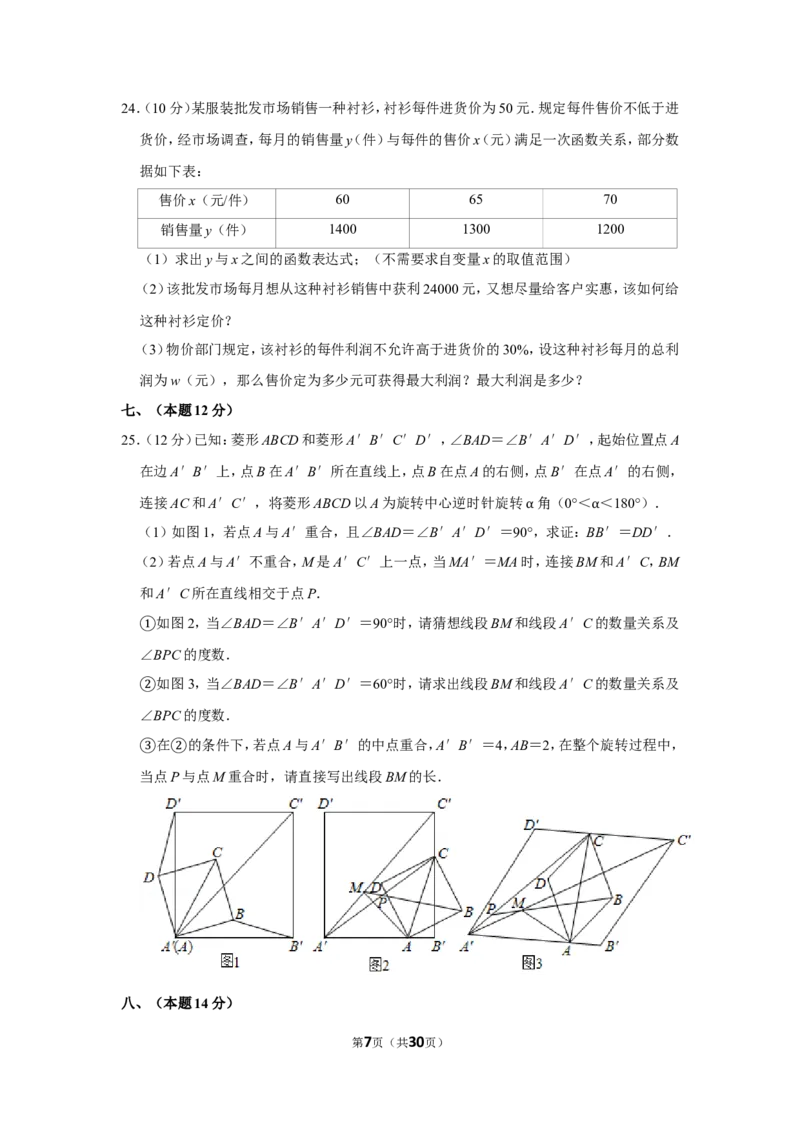
22.(10分)如图,已知△ABC,以AB为直径的 O交AC于点D,连接BD,∠CBD的平分线
交 O于点E,交AC于点F,且AF=AB.⊙
(1⊙)判断BC所在直线与 O的位置关系,并说明理由;
⊙
(2)若tan∠FBC= ,DF=2,求 O的半径.
⊙
六、(每小题10分,共20分)
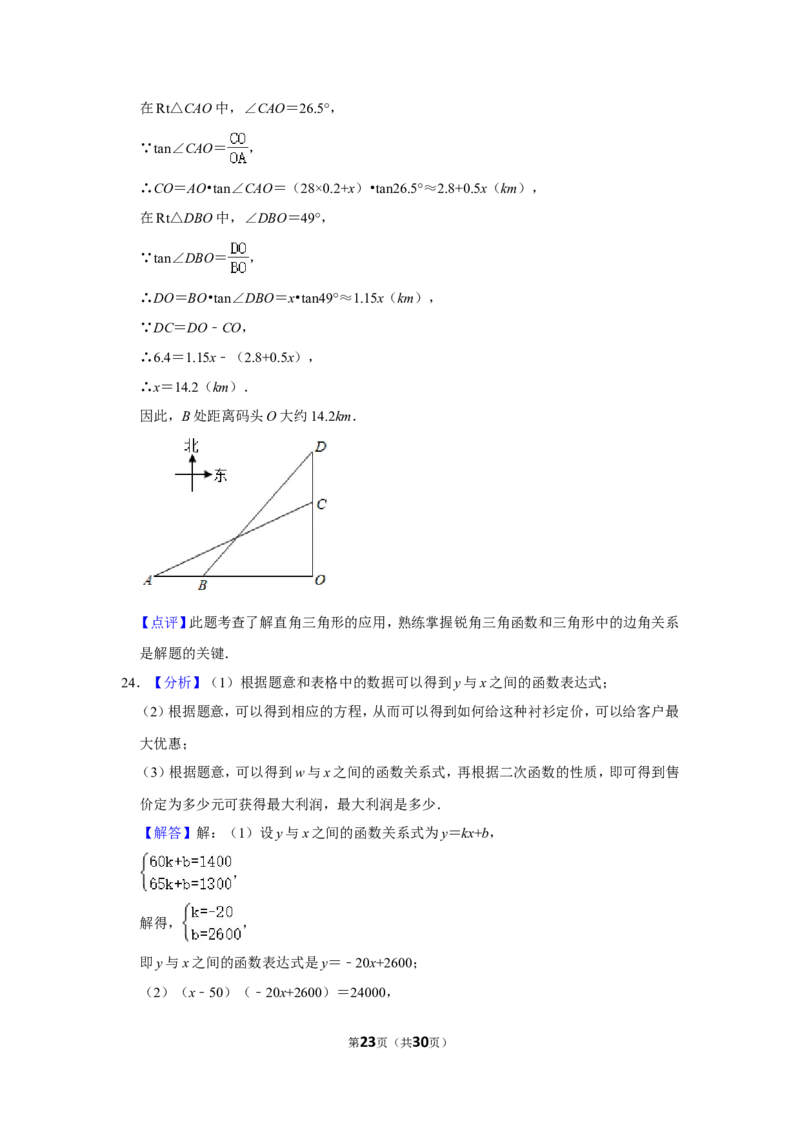
23.(10分)如图,小岛C和D都在码头O的正北方向上,它们之间距离为6.4km,一艘渔船
自西向东匀速航行,行驶到位于码头O的正西方向A处时,测得∠CAO=26.5°,渔船速度
为28km/h,经过0.2h,渔船行驶到了B处,测得∠DBO=49°,求渔船在B处时距离码头O
有多远?(结果精确到0.1km)
(参考数据:sin26.5°≈0.45,cos26.5°≈0.89,tan26.5°≈0.50,sin49°≈0.75,cos49°≈0.66,
tan49°≈1.15)
第6页(共30页)24.(10分)某服装批发市场销售一种衬衫,衬衫每件进货价为50元.规定每件售价不低于进
货价,经市场调查,每月的销售量y(件)与每件的售价x(元)满足一次函数关系,部分数
据如下表:
售价x(元/件) 60 65 70
销售量y(件) 1400 1300 1200
(1)求出y与x之间的函数表达式;(不需要求自变量x的取值范围)
(2)该批发市场每月想从这种衬衫销售中获利24000元,又想尽量给客户实惠,该如何给
这种衬衫定价?
(3)物价部门规定,该衬衫的每件利润不允许高于进货价的30%,设这种衬衫每月的总利
润为w(元),那么售价定为多少元可获得最大利润?最大利润是多少?
七、(本题12分)
25.(12分)已知:菱形ABCD和菱形A′B′C′D′,∠BAD=∠B′A′D′,起始位置点A
在边A′B′上,点B在A′B′所在直线上,点B在点A的右侧,点B′在点A′的右侧,
连接AC和A′C′,将菱形ABCD以A为旋转中心逆时针旋转 角(0°< <180°).
(1)如图1,若点A与A′重合,且∠BAD=∠B′A′D′=90α°,求证:BαB′=DD′.
(2)若点A与A′不重合,M是A′C′上一点,当MA′=MA时,连接BM和A′C,BM
和A′C所在直线相交于点P.
如图2,当∠BAD=∠B′A′D′=90°时,请猜想线段BM和线段A′C的数量关系及
①∠BPC的度数.
如图3,当∠BAD=∠B′A′D′=60°时,请求出线段BM和线段A′C的数量关系及
②∠BPC的度数.
在 的条件下,若点A与A′B′的中点重合,A′B′=4,AB=2,在整个旋转过程中,
③当点②P与点M重合时,请直接写出线段BM的长.
八、(本题14分)
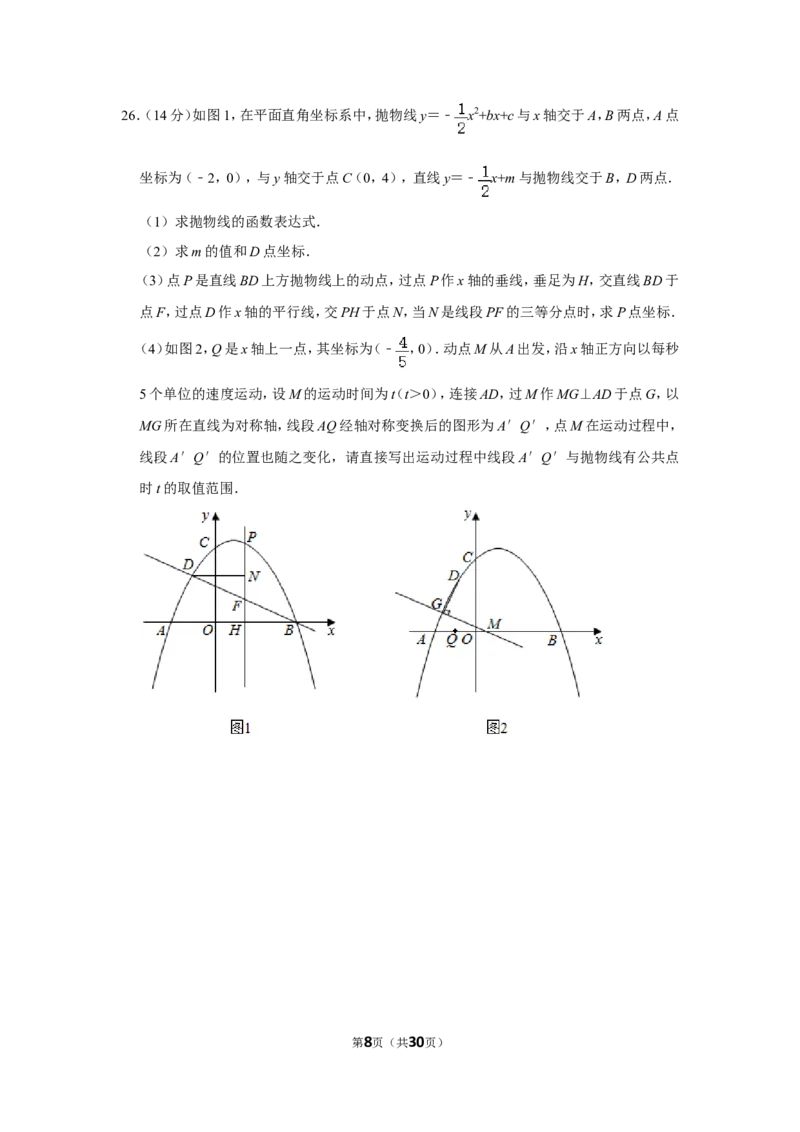
第7页(共30页)26.(14分)如图1,在平面直角坐标系中,抛物线y=﹣ x2+bx+c与x轴交于A,B两点,A点
坐标为(﹣2,0),与y轴交于点C(0,4),直线y=﹣ x+m与抛物线交于B,D两点.
(1)求抛物线的函数表达式.
(2)求m的值和D点坐标.
(3)点P是直线BD上方抛物线上的动点,过点P作x轴的垂线,垂足为H,交直线BD于
点F,过点D作x轴的平行线,交PH于点N,当N是线段PF的三等分点时,求P点坐标.
(4)如图2,Q是x轴上一点,其坐标为(﹣ ,0).动点M从A出发,沿x轴正方向以每秒
5个单位的速度运动,设M的运动时间为(t t>0),连接AD,过M作MG⊥AD于点G,以
MG所在直线为对称轴,线段AQ经轴对称变换后的图形为A′Q′,点M在运动过程中,
线段A′Q′的位置也随之变化,请直接写出运动过程中线段A′Q′与抛物线有公共点
时t的取值范围.
第8页(共30页)2020年辽宁省丹东市中考数学试卷
参考答案与试题解析
一、选择题(下列各题的备选答案中,只有一个是正确的.每小题3分,共24分)
1.【分析】根据负数的绝对值等于它的相反数解答.
【解答】解:﹣5的绝对值|﹣5|=5.
故选:B.
【点评】本题考查了绝对值的性质,熟记一个正数的绝对值是它本身;一个负数的绝对值
是它的相反数;0的绝对值是0是解题的关键.
2.【分析】用同底数幂的乘法法则计算A,用合并同类项法则计算B,用同底数幂的除法法则
计算C,用积和幂的乘方法则计算D.
【解答】解:因为a3•a3=a6≠2a3,故选项A计算不正确;
2a2+a2=3a2≠3a4,故选项B计算不正确;
a9÷a3=a6≠a3,故选项C计算不正确;
(﹣3a2)3=﹣27a6,故选项D计算正确;
故选:D.
【点评】本题考查了同底数幂的乘除法、合并同类项及积和幂的乘方法则.题目难度较小,
熟练掌握整式的运算法则是解决本题的关键.
3.【分析】根据从上边看得到的图形是俯视图,注意看到的棱用实线,直接看不到的用虚线,
可得答案.
【解答】解:该几何体的俯视图为
故选:C.
【点评】本题考查了简单组合体的三视图,从上边看得到的图形是俯视图.
4.【分析】根据二次根式的性质,可得被开方数大于等于0,解不等式即可得到x的取值范围.
【解答】解:根据题意得:9﹣3x≥0,
解得:x≤3.
故选:A.
【点评】本题考查的是函数自变量取值范围的求法.函数自变量的范围一般从三个方面考
虑:(1)当函数表达式是整式时,自变量可取全体实数;(2)当函数表达式是分式时,考虑
第9页(共30页)分式的分母不能为0;(3)当函数表达式是二次根式时,被开方数非负.
5.【分析】根据中心对称图形的概念,结合概率公式求解可得.
【解答】解:∵从这4张卡片中任意抽取一张共有4种等可能结果,其中抽到的卡片正面是
中心对称图形的是圆、平行四边形、正六边形这3种结果,
∴抽到的卡片正面是中心对称图形的概率是 ,
故选:C.
【点评】本题主要考查概率公式,解题的关键是掌握概率公式和中心对称图形的概念.
6.【分析】利用角平分线的性质、平行线的性质、三角形的外角与内角的关系,先求出∠D、
∠DCB的度数,再利用三角形的内角和定理求出∠CBD.
【解答】解:∵CO是△ABC的角平分线,
∴∠DCB=∠DCA.
∵BD∥AC,
∴∠A=∠DBA=45°,∠D=∠ACD=∠DCB.
∵∠AOD=∠D+∠DBA,
∴∠D=∠AOD﹣∠DBA
=80°﹣45°
=35°.
∴∠DCB=35°.
∵∠D+∠DCB+∠DBC=180°,
∴∠DBC=110°.
故选:B.
【点评】本题考查了三角形的内角和定理、平行线的性质、角平分线的性质等知识点.利用
平行线的性质,把分散的条件集中起来是解决本题的关键.
7.【分析】先根据平行四边形的判定可得四边形ABCD是平行四边形,根据平行四边形的性
质可得BC=AD=8 ,根据作图过程可得EB=EC,根据等边三角形的判定可得△EBC
第10页(共30页)是等边三角形,再根据等边三角形的性质即可求解.
【解答】解:∵在四边形ABCD中,AB∥CD,AB=CD,
∴四边形ABCD是平行四边形,
∴BC=AD=8 ,
由作图过程可得EB=EC,
∵∠B=60°,
∴△EBC是等边三角形,
∴△BCE的内切圆半径是 ×8 × × =4.
故选:A.
【点评】本题考查的是平行四边形的判定与性质,三角形的内切圆与内心,作图﹣基本作
图,熟知垂直平分线的作法是解答此题的关键.
8.【分析】由﹣ =2,得b=﹣4a,由点A坐标与点C坐标得a﹣b+c=0,2<c<3,由二次函
数图象可知a<0,则b>0,得出abc<0,故 不正确;
①
点N( ,y )关于对称轴x=2的对称点为( ,y ), >﹣ ,y随x的增大而增大,则y <
2 2 1
y ,故 正确;
2
②
由 ,解得﹣ <a<﹣ ,故 正确;
③
易求AB=6,DA=DB,则△ADB是等腰三角形,如果△ADB是等腰直角三角形,则点D
到AB的距离等于 AB=3,则 ,求出二次函数解析式为y=﹣ x2+ x+ ,
当x=0时,y= ,与点C在(0,2)与(0,3)之间(不包括这两点)矛盾,得出△ADB不可
能是等腰直角三角形,故 不正确.
④
【解答】解:∵二次函数y=ax2+bx+c(a≠0)的对称轴为:x=﹣ ,
∴﹣ =2,
第11页(共30页)∴b=﹣4a,
∵点A坐标为(﹣1,0),点C在(0,2)与(0,3)之间,且都在抛物线上,
∴a﹣b+c=0,2<c<3,
由二次函数图象可知,a<0,
∴b>0,
又∵c>0,
∴abc<0,故 不正确;
①
∵点N( ,y )关于对称轴x=2的对称点为( ,y ), >﹣ ,y随x的增大而增大,
2 2
∴y <y ,故 正确;
1 2
②
∵ ,
解得:﹣ <a<﹣ ,
故 正确;
∵③抛物线的顶点为D,对称轴为直线x=2,
∴点A与点B关于直线x=2对称,点D在直线x=2上,
∴AB=6,DA=DB,
∴△ADB是等腰三角形,
如果△ADB是等腰直角三角形,则点D到AB的距离等于 AB=3,即D(2,3),
则 ,
解得: ,
∴二次函数解析式为:y=﹣ x2+ x+ ,
当x=0时,y= ,与点C在(0,2)与(0,3)之间(不包括这两点)矛盾,
第12页(共30页)∴△ADB不可能是等腰直角三角形,故 不正确;
∴正确的有2个, ④
故选:B.
【点评】本题考查二次函数的图象与性质、二次函数解析式的求法、等腰三角形的判定等
知识,解题的关键是熟练掌握二次函数的图象与性质,属于中考常考题型.
二、填空题(每小题3分,共24分)
9.【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.
【解答】解:数据5800000用科学记数法表示为:5.8×106.
故答案为:5.8×106.
【点评】此题考查了科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中
1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
10.【分析】原式提取公因式,再利用平方差公式分解即可.
【解答】解:原式=mn(n2﹣4)
=mn(n+2)(n﹣2).
故答案为:mn(n+2)(n﹣2).
【点评】此题考查了提公因式法与公式法的综合运用,熟练掌握因式分解的方法是解本题
的关键.
11.【分析】直接利用y=kx+b与y轴交于(0,b),当b>0时,(0,b)在y轴的正半轴上,进而
得出答案.
【解答】解:∵一次函数y=﹣2x+b,且b>0,
∴它的图象经过第一、二、四象限,不经过第三象限.
故答案为:三.
【点评】此题主要考查了一次函数的性质,正确掌握一次函数图象分布规律是解题关键.
12.【分析】先根据方差的定义计算出乙成绩的方差,再与甲成绩的方差比较大小,方差小的
成绩更稳定,据此可得答案.
【解答】解:∵ = =5,
∴ = ×[(2﹣5)2+(3﹣5)2+(5﹣5)2+(7﹣5)2+(8﹣5)2]= ,
∵ =5< ,
∴成绩较稳定的是甲,
第13页(共30页)故答案为:甲.
【点评】本题主要考查方差,解题的关键是掌握方差的定义和方差的意义.
13.【分析】根据方程有两个实数根,得到此方程为一元二次方程且根的判别式大于等于0,
确定出m的范围即可.
【解答】解:∵关于x的方程(m+1)x2+3x﹣1=0有两个实数根,
∴△=9+4(m+1)≥0,且m+1≠0,
解得:m≥﹣ 且m≠﹣1.
故答案为:m≥﹣ 且m≠﹣1.
【点评】此题考查了根的判别式,弄清一元二次方程解的情况与根的判别式的关系是解本
题的关键.
14.【分析】根据题意设BC=4x,OC=5x,则OB=3x,根据反比例函数系数k的几何意义求得
C的坐标,解直角三角形求得AB的长,即可求得OA的长,从而求得D的坐标,代入解析
式即可求得k的值.
【解答】解:∵矩形ABCD的边AB在x轴上,点C在反比例函数y= 的图象上,
∴S△BOC = =3,
∵cos∠OCB= = ,
∴设BC=4x,OC=5x,则OB=3x,
∴ =3,解得x= ,
∴BC=2 ,OB= ,
∴C( ,2 ),
∵sin∠CAB= = ,
∴ = ,
∴AC=2 ,
第14页(共30页)∴AB= =4 ,
∴OA=AB﹣OB=4 ﹣ = ,
∴D(﹣ ,2 ),
∵点D在反比例函数y= 的图象上,
∴k=﹣ ×2 =﹣10,
故答案为﹣10.
【点评】本题考查了反比例函数图象上点的坐标特征,反比例函数系数k的几何意义,解直
角三角形等,求得D的坐标是解题的关键.
15.【分析】过点E作EH⊥BF于H.利用三角形的中位线定理以及直角三角形斜边中线定理
证明△BFE是顶角为120°的等腰三角形即可解决问题.
【解答】解:过点E作EH⊥BF于H.
∵AD=AC,∠DAC=90°,CD=8,
∴AD=AC=4 ,
∵DF=FC,AE=EC,
∴EF= AD=2 ,EF∥AD,
∴∠FEC=∠DAC=90°,
∵∠ABC=90°,AE=EC,
∴BE=AE=EC=2 ,
∴EF=BE=2 ,
第15页(共30页)∵∠BAD=105°,∠DAC=90°,
∴∠BAE=105°﹣90°=15°,
∴∠EAB=∠EBA=15°,
∴∠CEB=∠EAB+∠EBA=30°,
∴∠FEB=90°+30°=120°,
∴∠EFB=∠EBF=30°,
∵EH⊥BF,
∴EH= EF= ,FH= EH= ,
∴BF=2FH=2 ,
∴S△EFB = •BF•EH= ×2 × =2 .
故答案为2 .
【点评】本题考查三角形中位线定理,直角三角形斜边中线的性质,等腰三角形的判定和
性质,三角形的面积等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
16.【分析】首先证明CC ∥A A ,CC = A A ,推出 = ,求出第一个,第
1 2 3 1 2 3
二个三角形的面积,利用相似三角形的性质寻找规律,利用规律解决问题即可.
【解答】解:在矩形OAA B中,∵OA=3,AA =2,
1 1
∴∠A=90°,
∴OA = = = ,
1
∵ = = ,
第16页(共30页)∴ = ,
∵∠OA A =∠A=90°,
1 2
∴△OA A ∽△OAA ,
1 2 1
∴∠A OA =∠AOA ,
1 2 1
∵A B∥OA,
1
∴∠CA O=∠AOA ,
1 1
∴∠COA =∠CA O,
1 1
∴OC=CA ,
1
∵∠A OA +∠OA A =90°,∠OA C+∠A A C=90°,
2 1 2 1 1 2 1
∴∠CA A =∠CA A ,
2 1 1 2
∴CA =CA =OC,
1 2
同法可证OC =A C ,
1 3 1
∴CC ∥A A ,CC = A A ,
1 2 3 1 2 3
∴ = ,
∵A A = ,
1 2
∴OA = = = ,
2
∴A A = × = ,
2 3
∴CC = A A = ,
1 2 3
∴ = = × × = ,
同法可证 =S ,
由题意, = = = ,
∵△C A C ∽△C A C,
2 3 1 1 2
第17页(共30页)∴相似比为: = ,
∴ =( )2× = , = ,…,
由此规律可得,△C C A 的面积为 .
2019 2020 2022
故答案为 .
【点评】本题考查矩形的性质,相似三角形的判定和性质,三角形的面积,三角形的中位线
定理等知识,解题的关键是学会探究规律的方法,属于中考填空题中的压轴题.
三、解答题(每小题8分,共16分)
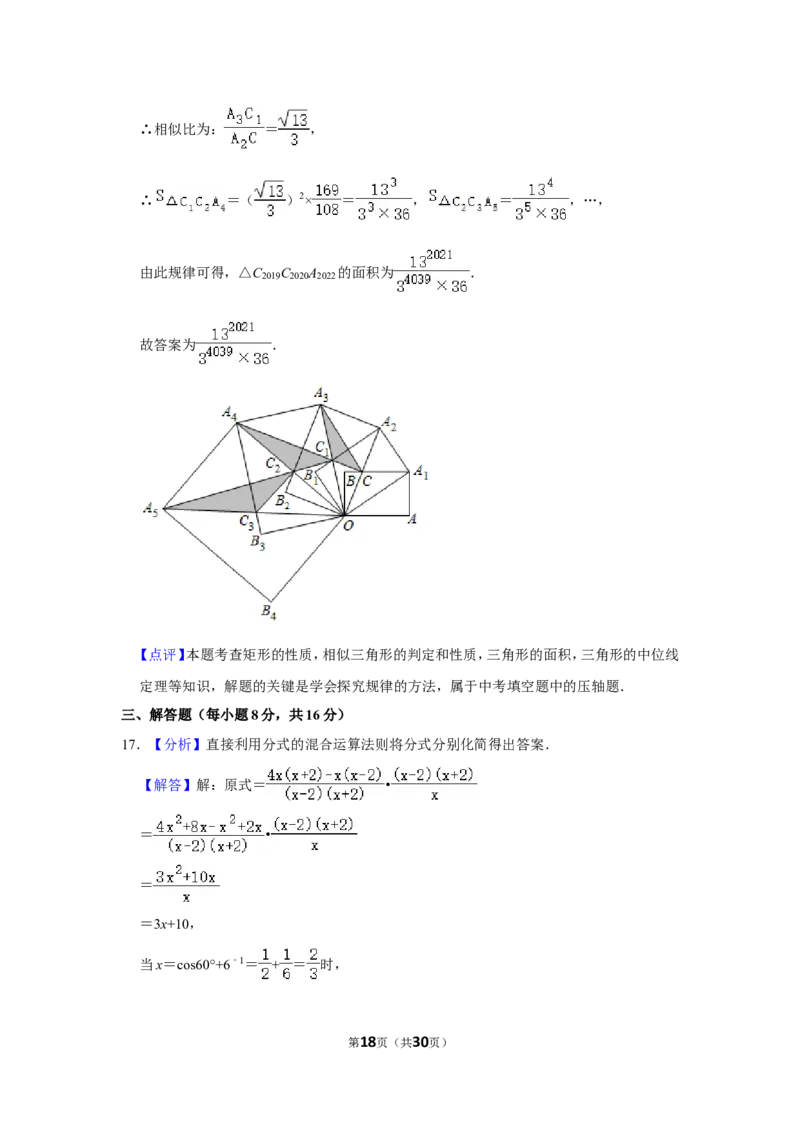
17.【分析】直接利用分式的混合运算法则将分式分别化简得出答案.
【解答】解:原式= •
= •
=
=3x+10,
当x=cos60°+6﹣1= + = 时,
第18页(共30页)原式=3× +10=12.
【点评】此题主要考查了分式的化简求值,正确化简分式是解题关键.
18.【分析】(1)利用网格和位似的性质画出△A B C ,再写出点A 的坐标即可,
1 1 1 1
(2)利用网格和旋转的性质画出△A B C ,先利用勾股定理求出OA的长,再根据弧长公
2 2 2
式即可求得答案.
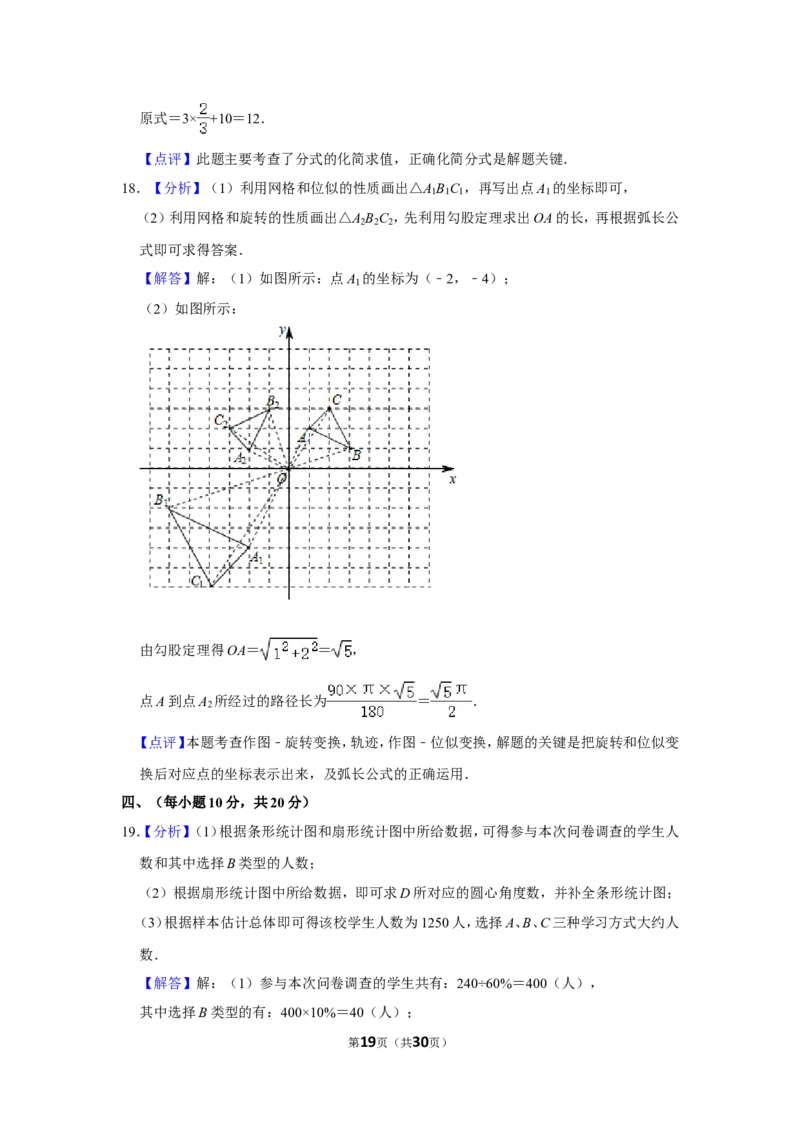
【解答】解:(1)如图所示:点A 的坐标为(﹣2,﹣4);
1
(2)如图所示:
由勾股定理得OA= = ,
点A到点A 所经过的路径长为 = .
2
【点评】本题考查作图﹣旋转变换,轨迹,作图﹣位似变换,解题的关键是把旋转和位似变
换后对应点的坐标表示出来,及弧长公式的正确运用.
四、(每小题10分,共20分)
19.【分析】(1)根据条形统计图和扇形统计图中所给数据,可得参与本次问卷调查的学生人
数和其中选择B类型的人数;
(2)根据扇形统计图中所给数据,即可求D所对应的圆心角度数,并补全条形统计图;
(3)根据样本估计总体即可得该校学生人数为1250人,选择A、B、C三种学习方式大约人
数.
【解答】解:(1)参与本次问卷调查的学生共有:240÷60%=400(人),
其中选择B类型的有:400×10%=40(人);
第19页(共30页)故答案为:400,40;
(2)在扇形统计图中,D所对应的圆心角度数为:
360°×(1﹣60%﹣10%﹣20%﹣6%)=14.4°,
∵400×20%=80(人),
∴选择C种学习方式的有80人.
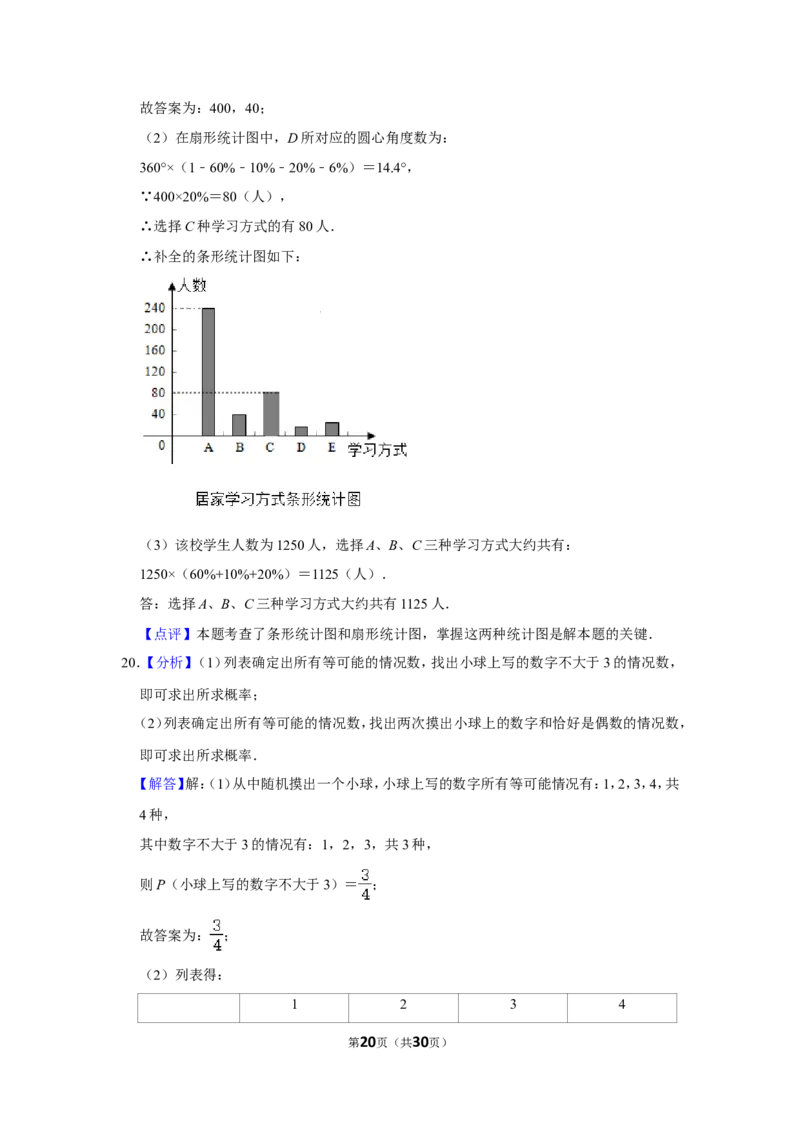
∴补全的条形统计图如下:
(3)该校学生人数为1250人,选择A、B、C三种学习方式大约共有:
1250×(60%+10%+20%)=1125(人).
答:选择A、B、C三种学习方式大约共有1125人.
【点评】本题考查了条形统计图和扇形统计图,掌握这两种统计图是解本题的关键.
20.【分析】(1)列表确定出所有等可能的情况数,找出小球上写的数字不大于3的情况数,
即可求出所求概率;
(2)列表确定出所有等可能的情况数,找出两次摸出小球上的数字和恰好是偶数的情况数,
即可求出所求概率.
【解答】解:(1)从中随机摸出一个小球,小球上写的数字所有等可能情况有:1,2,3,4,共
4种,
其中数字不大于3的情况有:1,2,3,共3种,
则P(小球上写的数字不大于3)= ;
故答案为: ;
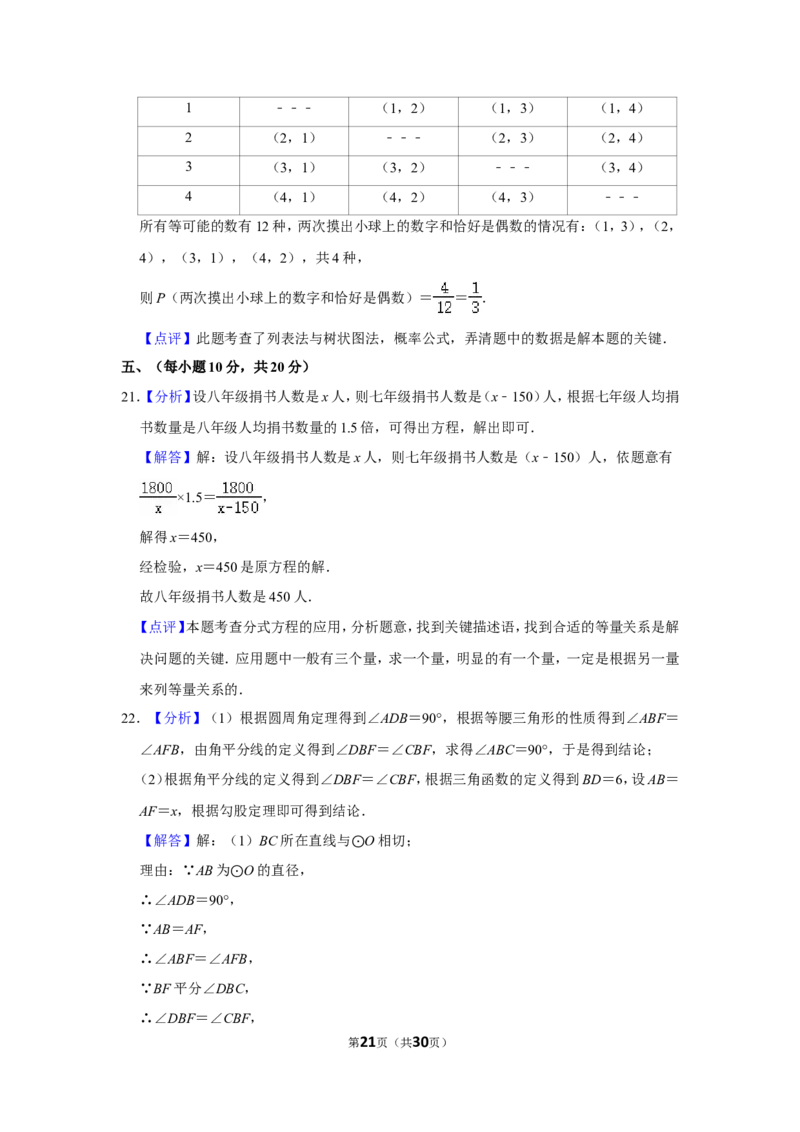
(2)列表得:
1 2 3 4
第20页(共30页)1 ﹣﹣﹣ (1,2) (1,3) (1,4)
2 (2,1) ﹣﹣﹣ (2,3) (2,4)
3 (3,1) (3,2) ﹣﹣﹣ (3,4)
4 (4,1) (4,2) (4,3) ﹣﹣﹣
所有等可能的数有12种,两次摸出小球上的数字和恰好是偶数的情况有:(1,3),(2,
4),(3,1),(4,2),共4种,
则P(两次摸出小球上的数字和恰好是偶数)= = .
【点评】此题考查了列表法与树状图法,概率公式,弄清题中的数据是解本题的关键.
五、(每小题10分,共20分)
21.【分析】设八年级捐书人数是x人,则七年级捐书人数是(x﹣150)人,根据七年级人均捐
书数量是八年级人均捐书数量的1.5倍,可得出方程,解出即可.
【解答】解:设八年级捐书人数是x人,则七年级捐书人数是(x﹣150)人,依题意有
×1.5= ,
解得x=450,
经检验,x=450是原方程的解.
故八年级捐书人数是450人.
【点评】本题考查分式方程的应用,分析题意,找到关键描述语,找到合适的等量关系是解
决问题的关键.应用题中一般有三个量,求一个量,明显的有一个量,一定是根据另一量
来列等量关系的.
22.【分析】(1)根据圆周角定理得到∠ADB=90°,根据等腰三角形的性质得到∠ABF=
∠AFB,由角平分线的定义得到∠DBF=∠CBF,求得∠ABC=90°,于是得到结论;
(2)根据角平分线的定义得到∠DBF=∠CBF,根据三角函数的定义得到BD=6,设AB=
AF=x,根据勾股定理即可得到结论.
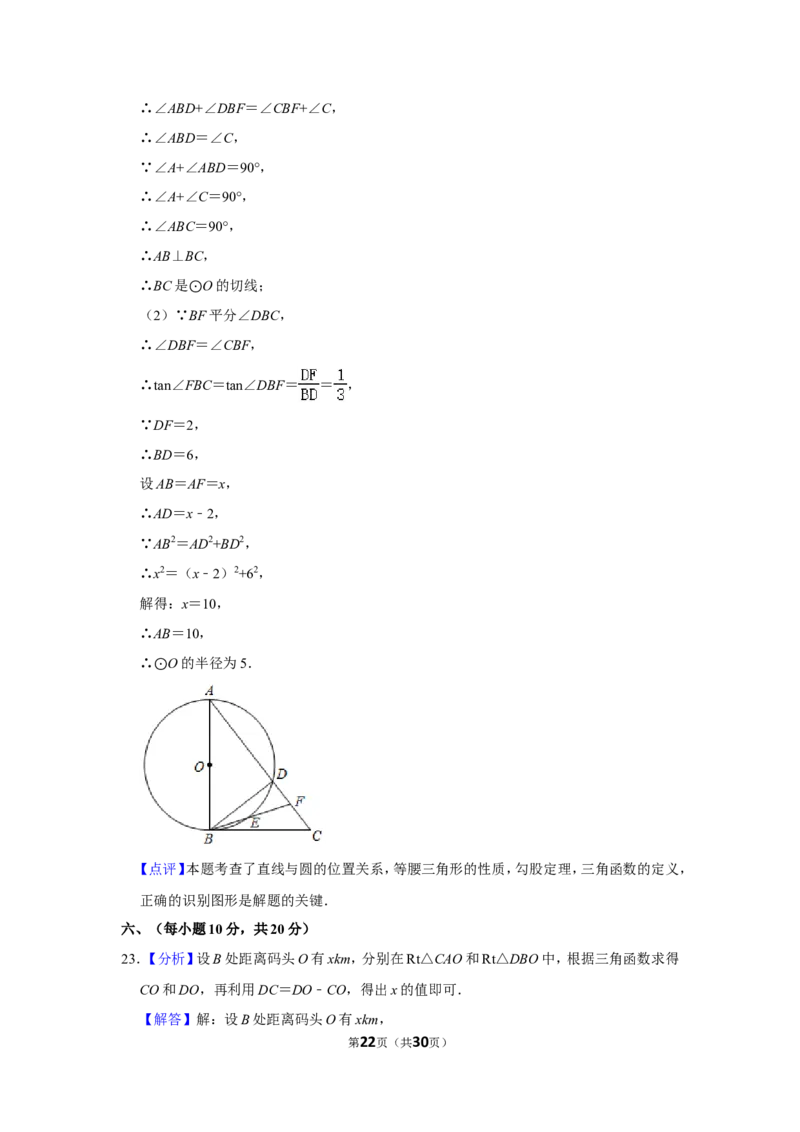
【解答】解:(1)BC所在直线与 O相切;
理由:∵AB为 O的直径, ⊙
∴∠ADB=90°,⊙
∵AB=AF,
∴∠ABF=∠AFB,
∵BF平分∠DBC,
∴∠DBF=∠CBF,
第21页(共30页)∴∠ABD+∠DBF=∠CBF+∠C,
∴∠ABD=∠C,
∵∠A+∠ABD=90°,
∴∠A+∠C=90°,
∴∠ABC=90°,
∴AB⊥BC,
∴BC是 O的切线;
(2)∵⊙BF平分∠DBC,
∴∠DBF=∠CBF,
∴tan∠FBC=tan∠DBF= = ,
∵DF=2,
∴BD=6,
设AB=AF=x,
∴AD=x﹣2,
∵AB2=AD2+BD2,
∴x2=(x﹣2)2+62,
解得:x=10,
∴AB=10,
∴ O的半径为5.
⊙
【点评】本题考查了直线与圆的位置关系,等腰三角形的性质,勾股定理,三角函数的定义,
正确的识别图形是解题的关键.
六、(每小题10分,共20分)
23.【分析】设B处距离码头O有xkm,分别在Rt△CAO和Rt△DBO中,根据三角函数求得
CO和DO,再利用DC=DO﹣CO,得出x的值即可.
【解答】解:设B处距离码头O有xkm,
第22页(共30页)在Rt△CAO中,∠CAO=26.5°,
∵tan∠CAO= ,
∴CO=AO•tan∠CAO=(28×0.2+x)•tan26.5°≈2.8+0.5x(km),
在Rt△DBO中,∠DBO=49°,
∵tan∠DBO= ,
∴DO=BO•tan∠DBO=x•tan49°≈1.15x(km),
∵DC=DO﹣CO,
∴6.4=1.15x﹣(2.8+0.5x),
∴x=14.2(km).
因此,B处距离码头O大约14.2km.
【点评】此题考查了解直角三角形的应用,熟练掌握锐角三角函数和三角形中的边角关系
是解题的关键.
24.【分析】(1)根据题意和表格中的数据可以得到y与x之间的函数表达式;
(2)根据题意,可以得到相应的方程,从而可以得到如何给这种衬衫定价,可以给客户最
大优惠;
(3)根据题意,可以得到w与x之间的函数关系式,再根据二次函数的性质,即可得到售
价定为多少元可获得最大利润,最大利润是多少.
【解答】解:(1)设y与x之间的函数关系式为y=kx+b,
,
解得, ,
即y与x之间的函数表达式是y=﹣20x+2600;
(2)(x﹣50)(﹣20x+2600)=24000,
第23页(共30页)解得,x =70,x =110,
1 2
∵尽量给客户优惠,
∴这种衬衫定价为70元;
(3)由题意可得,
w=(x﹣50)(﹣20x+2600)=﹣20(x﹣90)2+32000,
∵该衬衫的每件利润不允许高于进货价的30%,每件售价不低于进货价,
∴50≤x,(x﹣50)÷50≤30%,
解得,50≤x≤65,
∴当x=65时,w取得最大值,此时w=19500,
答:售价定为65元可获得最大利润,最大利润是19500元.
【点评】本题考查二次函数的应用、一元二次方程的应用,解答本题的关键是明确题意,利
用二次函数的性质和方程的知识解答.
七、(本题12分)
25.【分析】(1)证明△ADD′≌△BAB′(SAS)可得结论.
(2) 证明△AA′C∽△MAB,可得结论.
证明①方法类似 .
②求出A′C,利①用 中结论计算即可.
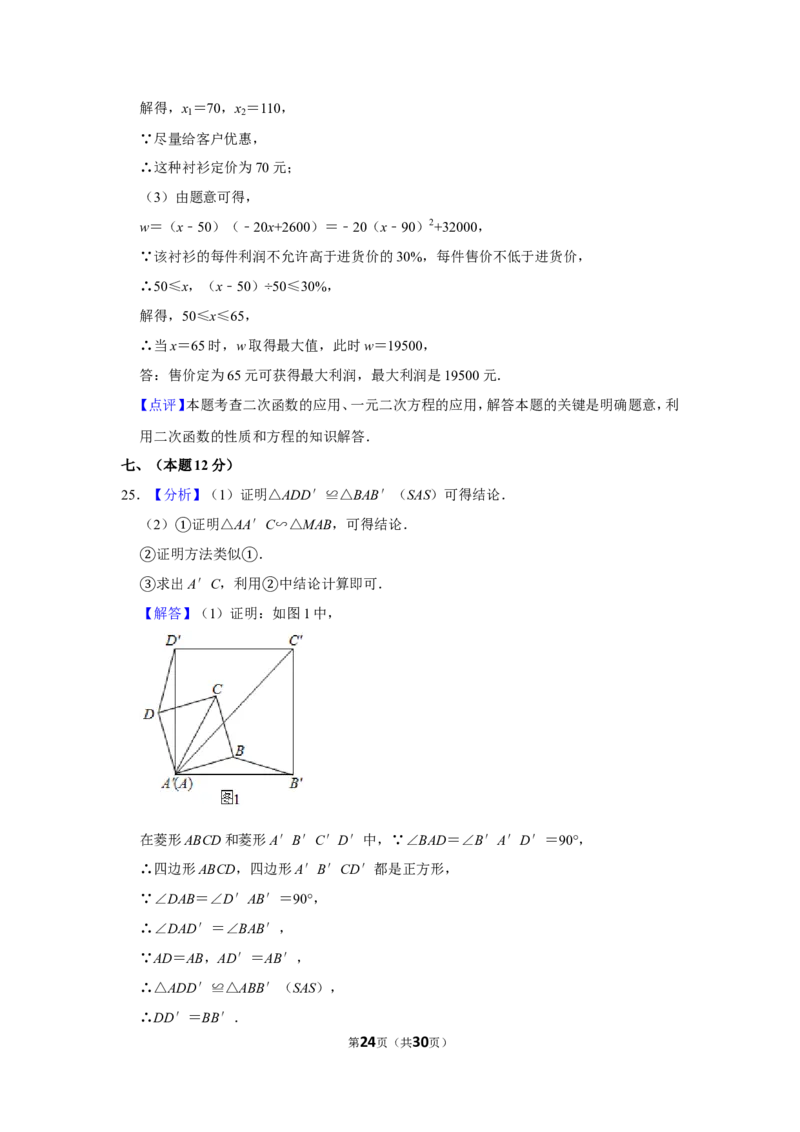
③【解答】(1)证明:②如图1中,
在菱形ABCD和菱形A′B′C′D′中,∵∠BAD=∠B′A′D′=90°,
∴四边形ABCD,四边形A′B′CD′都是正方形,
∵∠DAB=∠D′AB′=90°,
∴∠DAD′=∠BAB′,
∵AD=AB,AD′=AB′,
∴△ADD′≌△ABB′(SAS),
∴DD′=BB′.
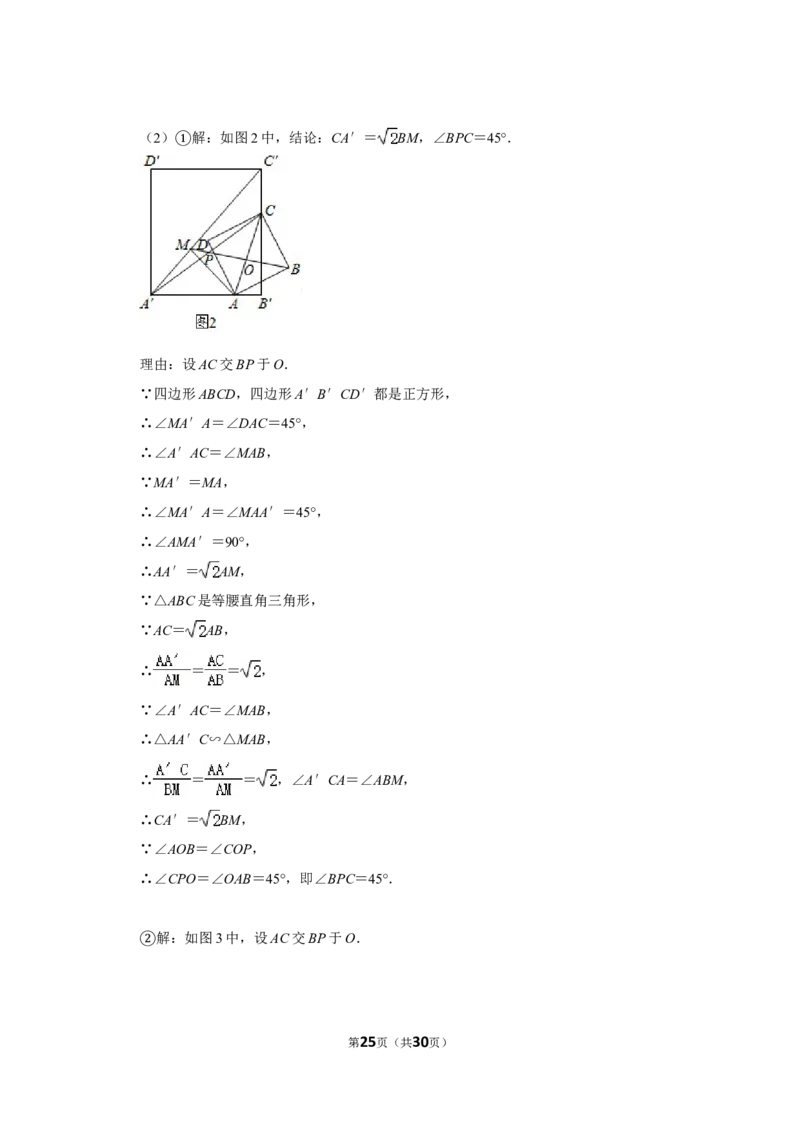
第24页(共30页)(2) 解:如图2中,结论:CA′= BM,∠BPC=45°.
①
理由:设AC交BP于O.
∵四边形ABCD,四边形A′B′CD′都是正方形,
∴∠MA′A=∠DAC=45°,
∴∠A′AC=∠MAB,
∵MA′=MA,
∴∠MA′A=∠MAA′=45°,
∴∠AMA′=90°,
∴AA′= AM,
∵△ABC是等腰直角三角形,
∵AC= AB,
∴ = = ,
∵∠A′AC=∠MAB,
∴△AA′C∽△MAB,
∴ = = ,∠A′CA=∠ABM,
∴CA′= BM,
∵∠AOB=∠COP,
∴∠CPO=∠OAB=45°,即∠BPC=45°.
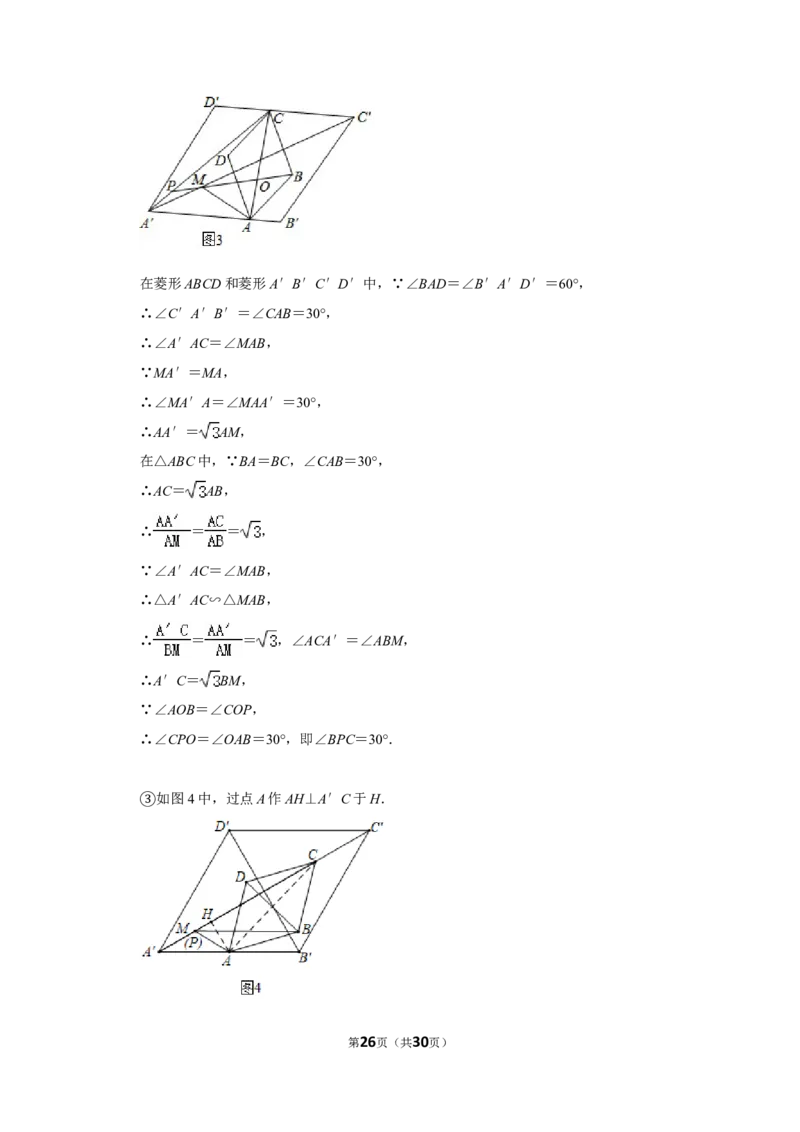
解:如图3中,设AC交BP于O.
②
第25页(共30页)在菱形ABCD和菱形A′B′C′D′中,∵∠BAD=∠B′A′D′=60°,
∴∠C′A′B′=∠CAB=30°,
∴∠A′AC=∠MAB,
∵MA′=MA,
∴∠MA′A=∠MAA′=30°,
∴AA′= AM,
在△ABC中,∵BA=BC,∠CAB=30°,
∴AC= AB,
∴ = = ,
∵∠A′AC=∠MAB,
∴△A′AC∽△MAB,
∴ = = ,∠ACA′=∠ABM,
∴A′C= BM,
∵∠AOB=∠COP,
∴∠CPO=∠OAB=30°,即∠BPC=30°.
如图4中,过点A作AH⊥A′C于H.
③
第26页(共30页)由题意AB=BC=CD=AD=2,可得AC= AB=2 ,
在Rt△A′AH中,A′H= AA′=1,A AH= ,
在Rt△AHC中,CH= = = ,
∴A′C=A′H+CH= + ,
由 可知,A′C= BM,
②
∴BM=1+ .
【点评】本题属于四边形综合题,考查了菱形的性质,正方形的性质,等边三角形的判定和
性质等知识,解题的关键是正确寻找全等三角形或相似三角形解决问题,属于中考压轴题.
八、(本题14分)
26.【分析】(1)利用待定系数法解决问题即可.
(2)求出点B的坐标,可得直线BD的解析式,构建方程组确定点D坐标即可.
(3)设P(a,﹣ a2+a+4),则N(a, ),F(a,﹣ a+2)推出PN=﹣ a2+a+4﹣ =﹣
a2+a+ ,NF= ﹣(﹣ a+2)= a+ ,由N是线段PF的三等分点,推出PN=2NF或
NF=2PN,构建方程求解即可.
(4)首先证明QQ′∥AD,由题意直线QQ′的解析式为y= x+2,设直线QQ′交抛物线
于E,利用方程组求出点E的坐标,求出两种特殊情形t的值即可判断.
【解答】解:(1)把A(﹣2,0),C(0,4)代入y=﹣ x2+bx+c,
得到 ,
解得 ,
∴抛物线的解析式为y=﹣ x2+x+4.
(2)令y=0,则有﹣ x2+x+4=0,
解得x=﹣2或4,
第27页(共30页)∴B(4,0),
把B(4,0)代入y=﹣ x+m,得到m=2,
∴直线BD的解析式为y=﹣ x+2,
由 ,解得 或 ,
∴D(﹣1, ).
(3)设P(a,﹣ a2+a+4),
则N(a, ),F(a,﹣ a+2),
∴PN=﹣ a2+a+4﹣ =﹣ a2+a+ ,NF= ﹣(﹣ a+2)= a+ ,
∵N是线段PF的三等分点,
∴PN=2NF或NF=2PN,
∴﹣ a2+a+ =a+1或 a+ =﹣a2+2a+3,
解得a=±1或﹣1或 ,
∵a>0,
∴a=1或 ,
∴P(1, )或( , ).
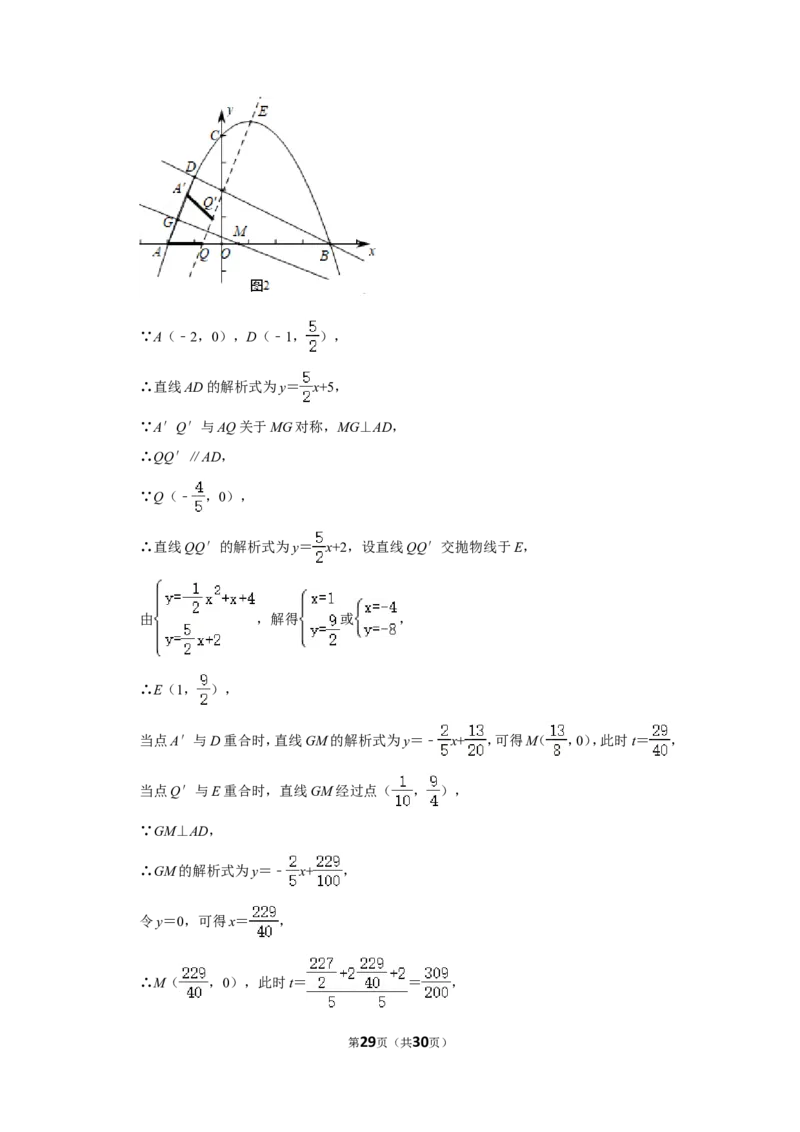
(4)如图2中,
第28页(共30页)∵A(﹣2,0),D(﹣1, ),
∴直线AD的解析式为y= x+5,
∵A′Q′与AQ关于MG对称,MG⊥AD,
∴QQ′∥AD,
∵Q(﹣ ,0),
∴直线QQ′的解析式为y= x+2,设直线QQ′交抛物线于E,
由 ,解得 或 ,
∴E(1, ),
当点A′与D重合时,直线GM的解析式为y=﹣ x+ ,可得M( ,0),此时t= ,
当点Q′与E重合时,直线GM经过点( , ),
∵GM⊥AD,
∴GM的解析式为y=﹣ x+ ,
令y=0,可得x= ,
∴M( ,0),此时t= = ,
第29页(共30页)观察图象可知,满足条件的t的值为 ≤t≤ .
【点评】本题考查二次函数综合题,一次函数的性质,轴对称变换等知识,解题的关键是理
解题意,学会用分类讨论的思想思考问题,学会寻找特殊点解决问题,属于中考压轴题.
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布
日期:2020/9/14 12:30:47;用户:18366185883;邮箱:18366185883;学号:22597006
第30页(共30页)