文档内容
2021 年广西北部湾南宁中考数学试卷
一、选择题(本大题共12小题,共36分)
下列各数是有理数的是()
1.
A. π B. √2 C. √33 D. 0
如图是一个几何体的主视图,则该几何体是()
2.
A.
B.
C.
D.
如图,小明从A入口进入博物馆参观,参观后可从B,C,D三个出口
3. 走出,他恰好从C出口走出的概率是()
1
A.
4
1
B.
3
第 页,共 页
1 11
C.
2
2
D.
3
我国天问一号火星探测器于2021年5月15日成功着陆火星表面.经测算,地球跟火星最远距离约
4. 400000000千米,其中数据400000000科学记数法表示为()
A. 4×109 B. 40×107 C. 4×108 D. 0.4×109
如图是某市一天的气温随时间变化的情况,下列说法正确的是()
5.
A. 这一天最低温度是−4℃ B. 这一天12时温度最高
C. 最高温比最低温高8℃ D. 0时至8时气温呈下降趋势
下列运算正确的是()
6.
A. a2 ⋅a3=a5 B. (a2 ) 3=a5 C. a6÷a2=a3 D. 3a2−2a=a2
平面直角坐标系内与点P(3,4)关于原点对称的点的坐标是()
7.
A. (−3,4) B. (−3,−4) C. (3,−4) D. (4,3)
如图,⊙O的半径OB为4,OC⊥AB于点D,∠BAC=30°,则OD的长
8. 是()
A. √2
B. √3
C. 2
D. 3
第 页,共 页
2 2一次函数y=2x+1的图象不经过()
9.
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
《九章算术》是人类科学史上应用数学的“算经之首”,书中记载:今有三人共车,二车空;二人
10. 共车,九人步.问:人与车各几何?译文:若3人坐一辆车,则两辆车是空的;若2人坐一辆车,则9
人需要步行,问:人与车各多少?设有x辆车,人数为y,根据题意可列方程组为()
{y=3x−2 {y=3(x−2) {y=3x−2 {y=3(x−2)
A. B. C. D.
y=2x+9 y=2x+9 y=2x−9 y=2x−9
如图,矩形纸片ABCD,AD:AB=√2:1,点E,F分别在AD,BC上,
11. 把纸片如图沿EF折叠,点A,B的对应点分别为A′,B′,连接AA′并
EF
延长交线段CD于点G,则 的值为()
AG
√2
A.
2
2
B.
3
1
C.
2
√5
D.
3
{a,a≥b
定义一种运算:a∗b= ,则不等式(2x+1)∗(2−x)>3的解集是()
b,a1或x< B. −11或x<−1 D. x> 或x<−1
3
二、填空题(本大题共6小题,共18分)
1
要使分式 有意义,则x的取值范围是______.
x−2
13.
第 页,共 页
3 1分解因式:a2−4b2=______.
14.
如图,从
15. 楼顶A
处看楼下
荷塘C
处的俯角
为45°,看楼下荷塘D处的俯角为60°,已知楼高AB为30米,则荷塘的宽CD为______ 米(结果保
留根号).
为了庆祝中国共产党成立100周年,某校举行“党在我心中”演讲比赛,评委将从演讲内容,演讲
16. 能力,演讲效果三个方面给选手打分,各项成绩均按百分制计,然后再按演讲内容占50%,演讲能
力占40%,演讲效果占10%,计算选手的综合成绩(百分制).小婷的三项成绩依次是84,95,90,她
的综合成绩是______ .
如图,从一块边长为2,∠A=120°的菱形铁片上剪出一个扇形,这
17. 个扇形在以A为圆心的圆上(阴影部分),且圆弧与BC,CD分别相切
于点E,F,将剪下来的扇形围成一个圆锥,则圆锥的底面圆半径是
______ .
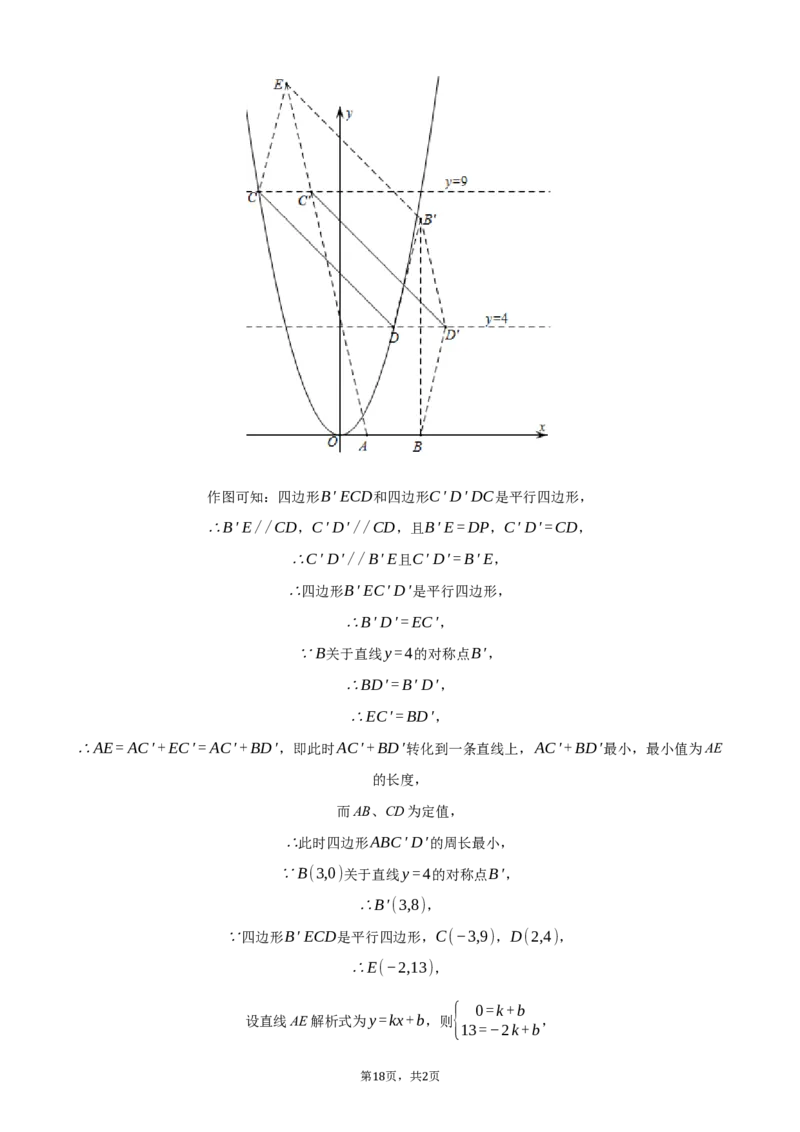
如图,已知点A(3,0),B(1,0),两点
18. C(−3,9),D(2,4)在抛物线y=x2上,
向左或向右平移抛物线后,C,D的对
应点分别为C′,D′.当四边形
ABC′D′的周长最小时,抛物线的解
析式为______ .
第 页,共 页
4 2三、解答题(本大题共8小题,共66分)
1
计算:23×(− +1)÷(1−3).
2
19.
x x
解分式方程: = +1.
x+1 3x+3
20.
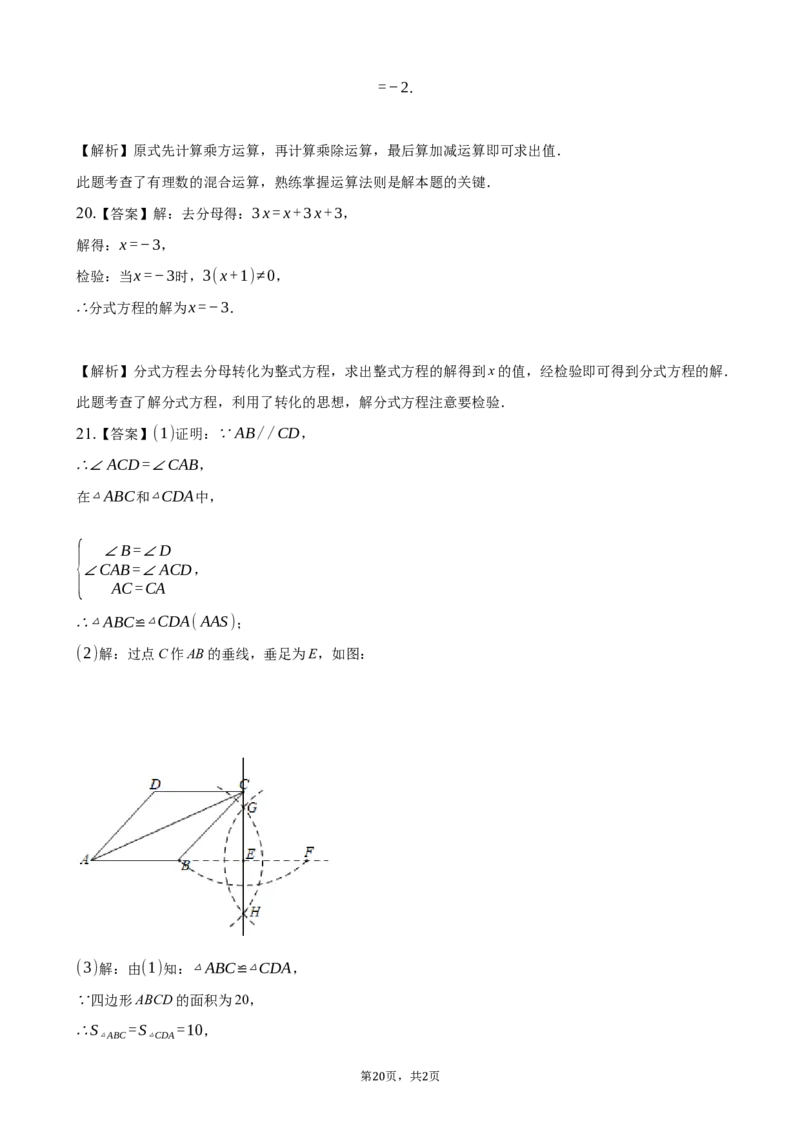
如图,四边形ABCD中,AB//CD,∠B=∠D,连接AC.
21. (1)求证:△ABC △CDA;
(2)尺规作图:过点≌C作AB的垂线,垂足为E(不要求写作法,保
留作图痕迹);
(3)在(2)的条件下,已知四边形ABCD的面积为20,AB=5,求CE的长.
第 页,共 页
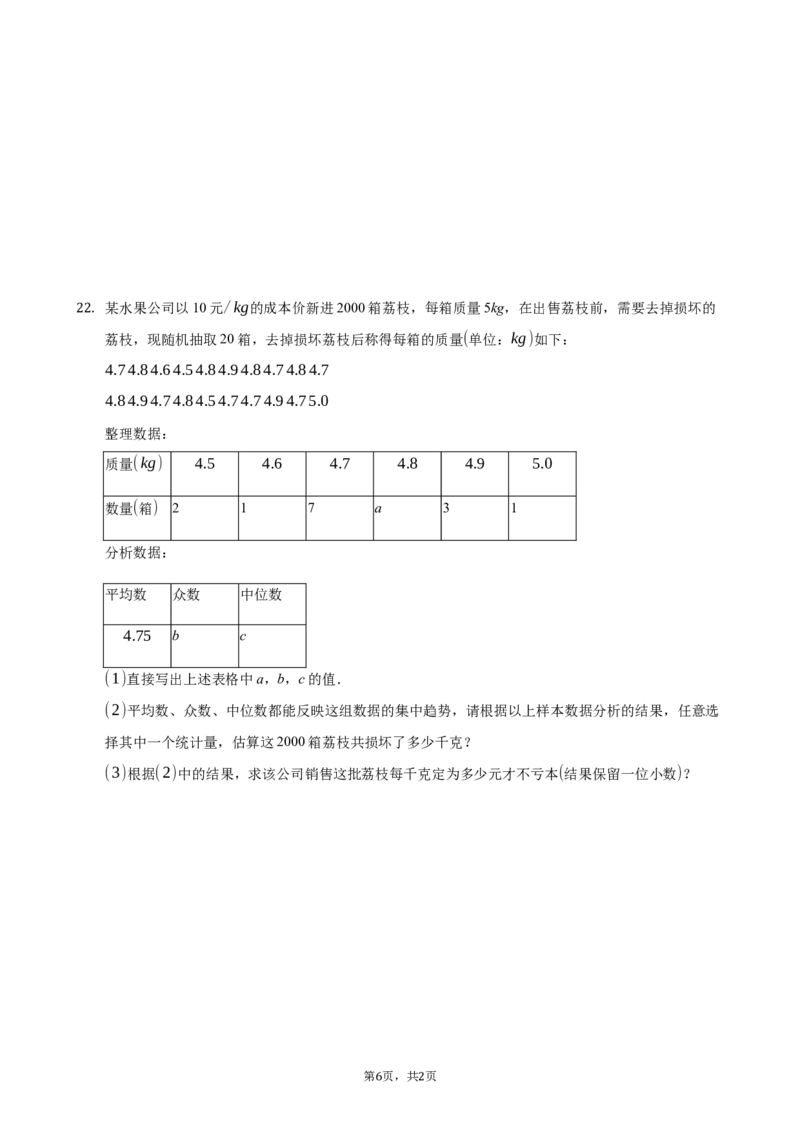
5 1某水果公司以10元/kg的成本价新进2000箱荔枝,每箱质量5kg,在出售荔枝前,需要去掉损坏的
22. 荔枝,现随机抽取20箱,去掉损坏荔枝后称得每箱的质量(单位:kg)如下:
4.74.84.64.54.84.94.84.74.84.7
4.84.94.74.84.54.74.74.94.75.0
整理数据:
质量(kg) 4.5 4.6 4.7 4.8 4.9 5.0
数量(箱) 2 1 7 a 3 1
分析数据:
平均数 众数 中位数
4.75 b c
(1)直接写出上述表格中a,b,c的值.
(2)平均数、众数、中位数都能反映这组数据的集中趋势,请根据以上样本数据分析的结果,任意选
择其中一个统计量,估算这2000箱荔枝共损坏了多少千克?
(3)根据(2)中的结果,求该公司销售这批荔枝每千克定为多少元才不亏本(结果保留一位小数)?
第 页,共 页
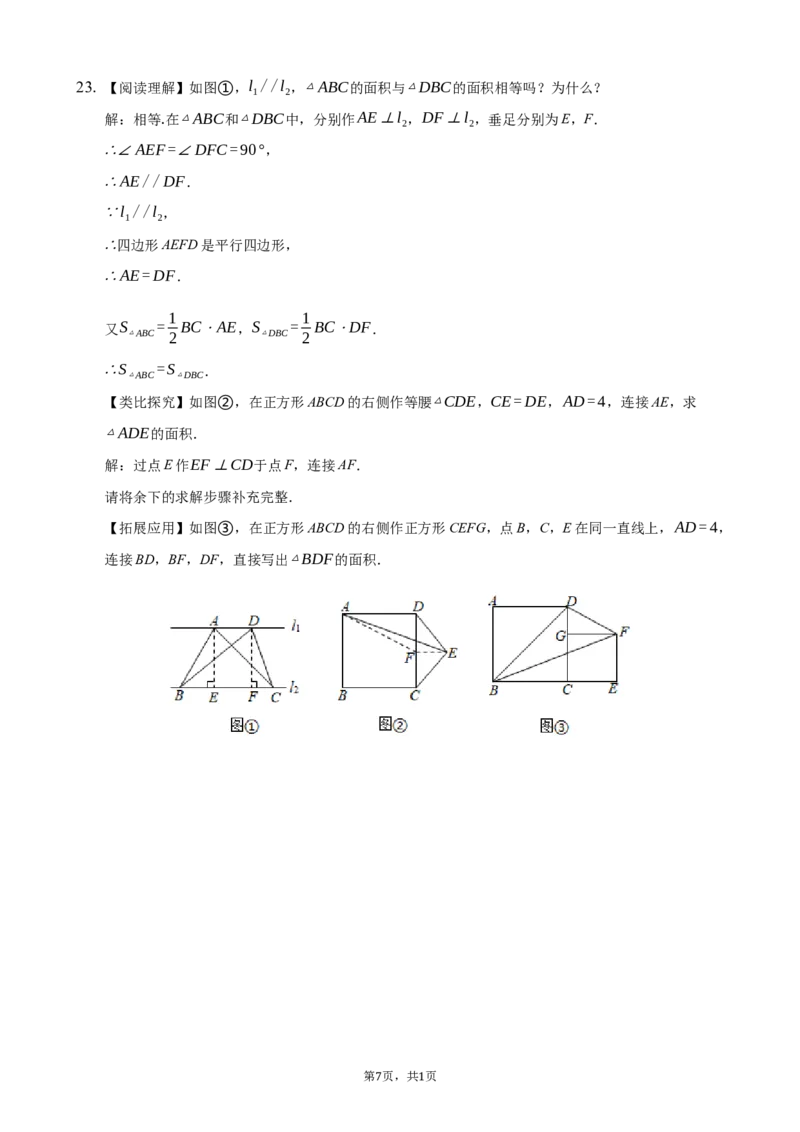
6 223. 【阅读理解】如图①,l //l ,△ABC的面积与△DBC的面积相等吗?为什么?
1 2
解:相等.在△ABC和△DBC中,分别作AE⊥l ,DF⊥l ,垂足分别为E,F.
2 2
∴∠AEF=∠DFC=90°,
∴AE//DF.
∵l //l ,
1 2
∴四边形AEFD是平行四边形,
∴AE=DF.
1 1
又S = BC⋅AE,S = BC⋅DF.
△ABC 2 △DBC 2
∴S =S .
△ABC △DBC
【类比探究】如图②,在正方形ABCD的右侧作等腰△CDE,CE=DE,AD=4,连接AE,求
△ADE的面积.
解:过点E作EF⊥CD于点F,连接AF.
请将余下的求解步骤补充完整.
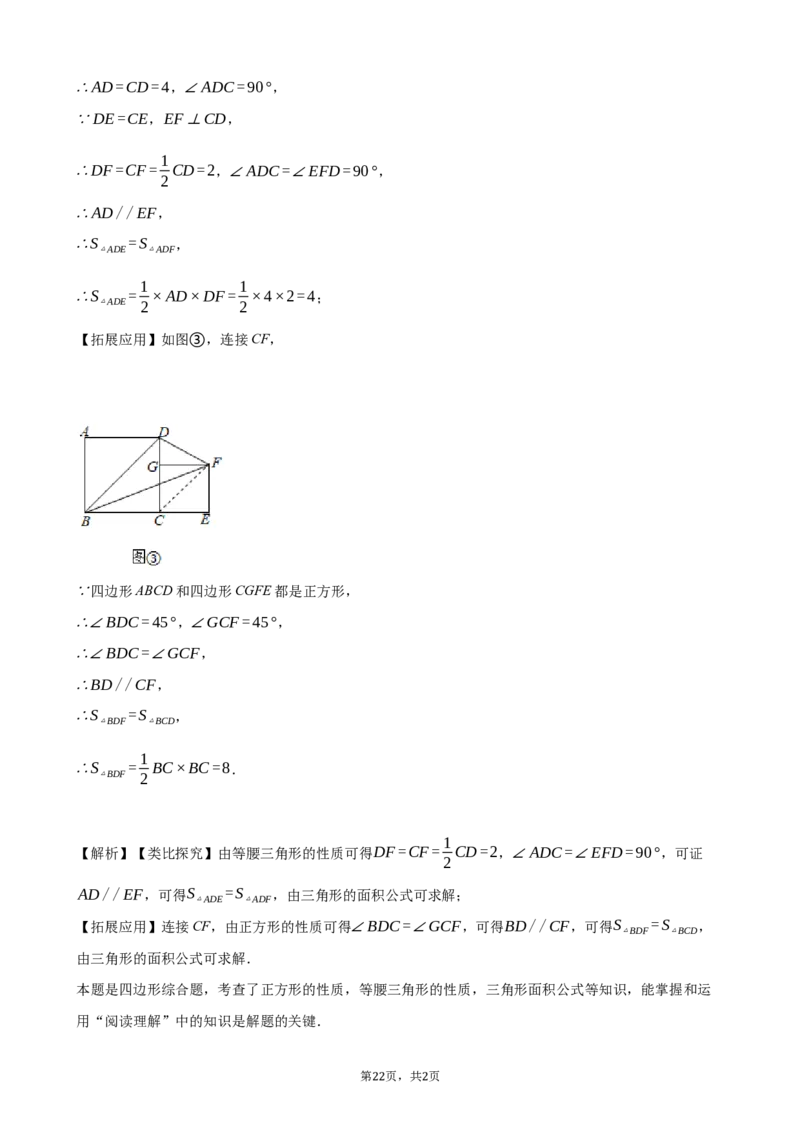
【拓展应用】如图③,在正方形ABCD的右侧作正方形CEFG,点B,C,E在同一直线上,AD=4,
连接BD,BF,DF,直接写出△BDF的面积.
第 页,共 页
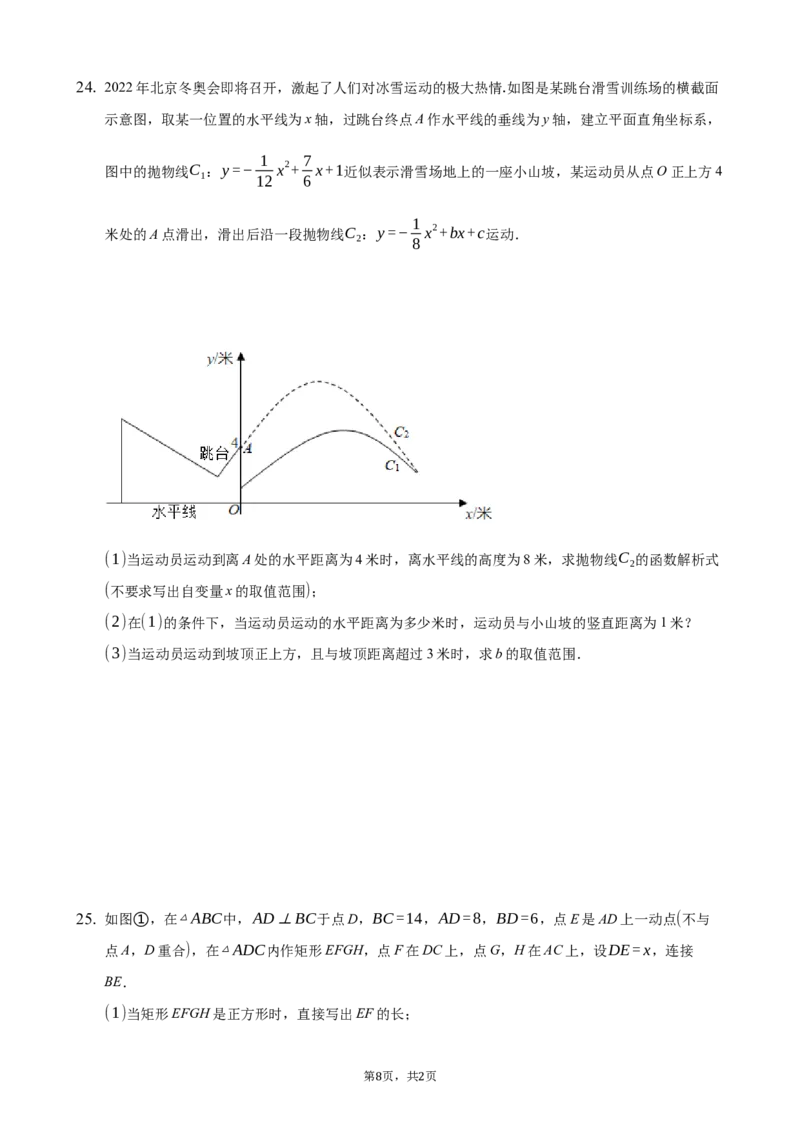
7 124. 2022年北京冬奥会即将召开,激起了人们对冰雪运动的极大热情.如图是某跳台滑雪训练场的横截面
示意图,取某一位置的水平线为x轴,过跳台终点A作水平线的垂线为y轴,建立平面直角坐标系,
1 7
图中的抛物线C :y=− x2+ x+1近似表示滑雪场地上的一座小山坡,某运动员从点O正上方4
1 12 6
1
米处的A点滑出,滑出后沿一段抛物线C :y=− x2+bx+c运动.
2 8
(1)当运动员运动到离A处的水平距离为4米时,离水平线的高度为8米,求抛物线C 的函数解析式
2
(不要求写出自变量x的取值范围);
(2)在(1)的条件下,当运动员运动的水平距离为多少米时,运动员与小山坡的竖直距离为1米?
(3)当运动员运动到坡顶正上方,且与坡顶距离超过3米时,求b的取值范围.
25. 如图①,在△ABC中,AD⊥BC于点D,BC=14,AD=8,BD=6,点E是AD上一动点(不与
点A,D重合),在△ADC内作矩形EFGH,点F在DC上,点G,H在AC上,设DE=x,连接
BE.
(1)当矩形EFGH是正方形时,直接写出EF的长;
第 页,共 页
8 2S
(2)设△ABE的面积为S ,矩形EFGH的面积为S ,令y= 1 ,求y关于x的函数解析式(不要求写出
1 2 S
2
自变量x的取值范围);
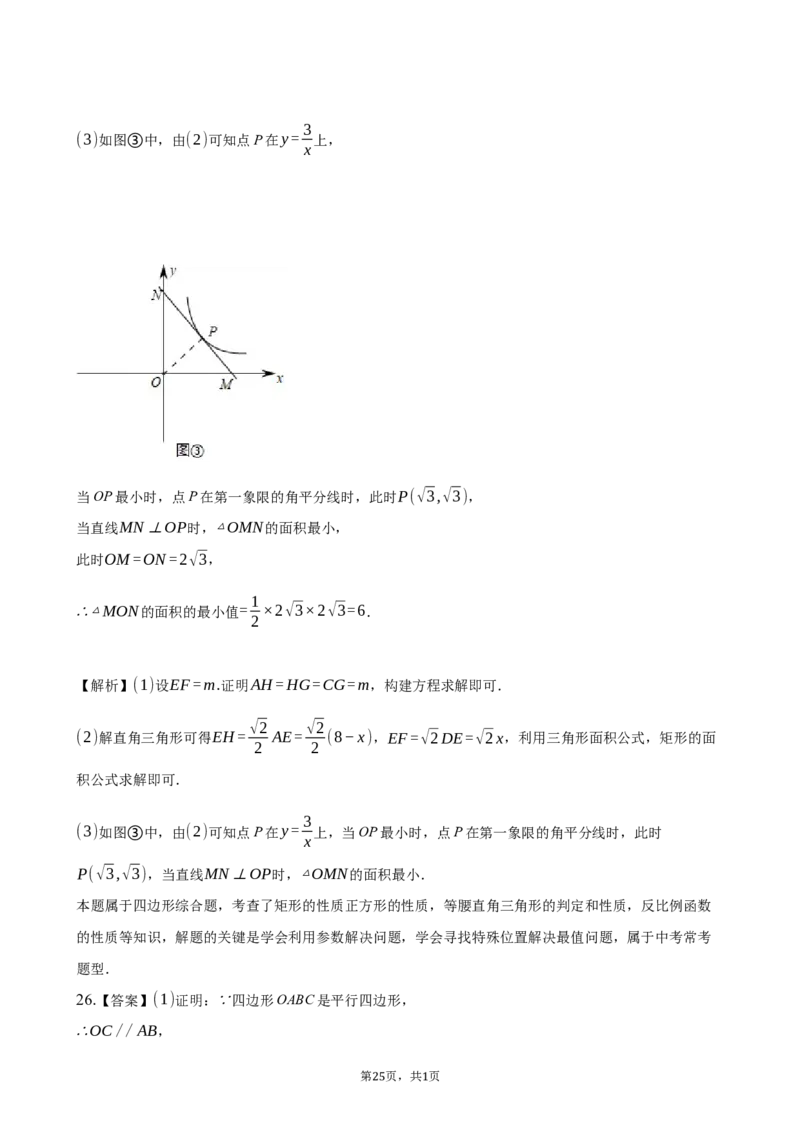
(3)如图②,点P(a,b)是(2)中得到的函数图象上的任意一点,过点P的直线l分别与x轴正半轴,
y轴正半轴交于M,N两点,求△OMN面积的最小值,并说明理由.
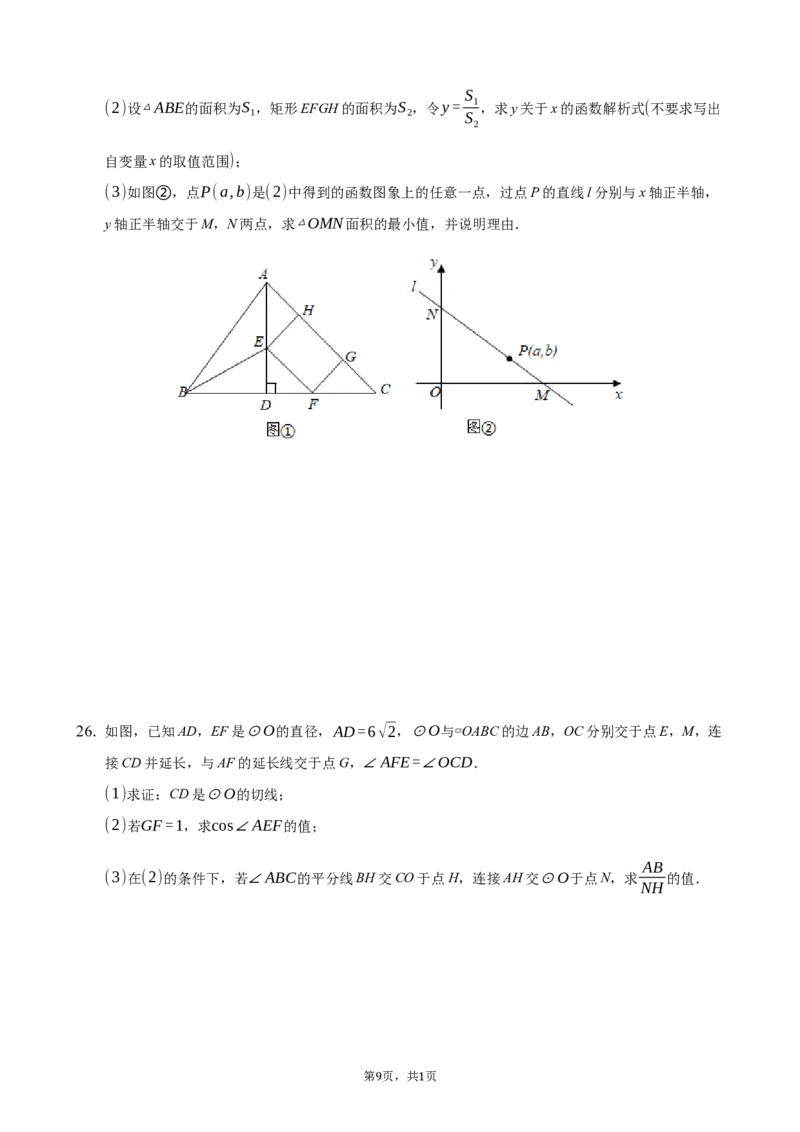
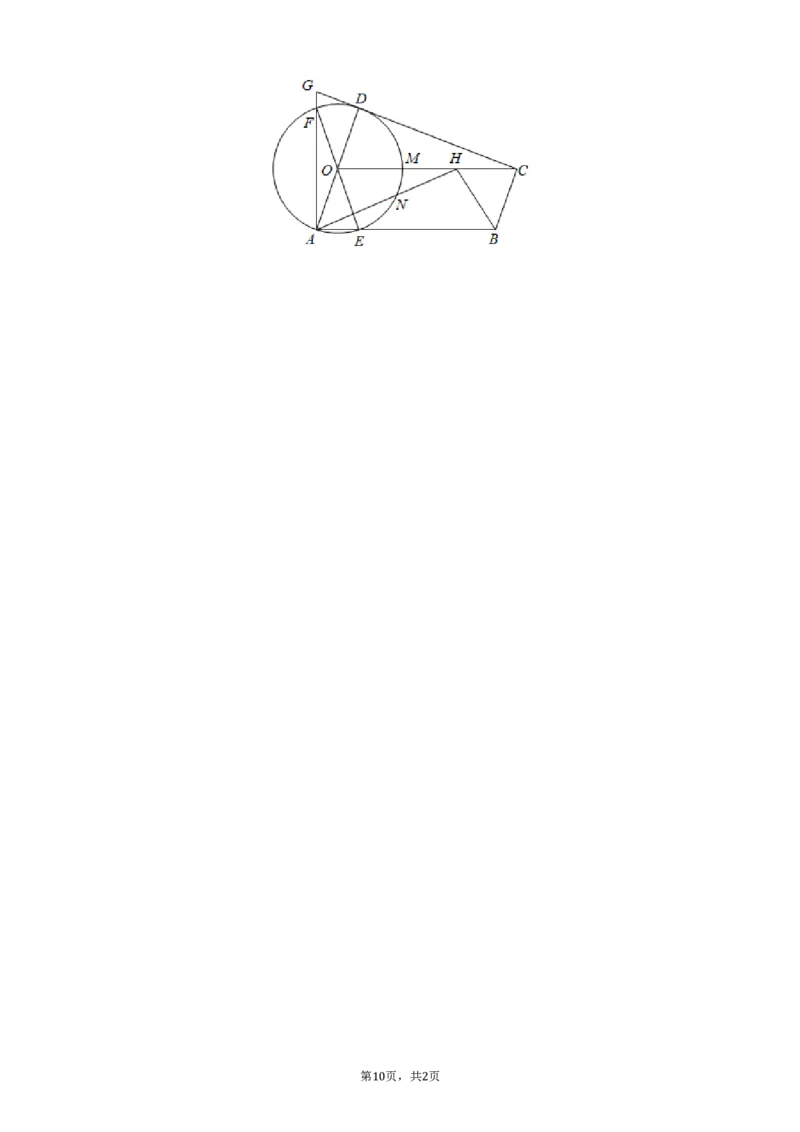
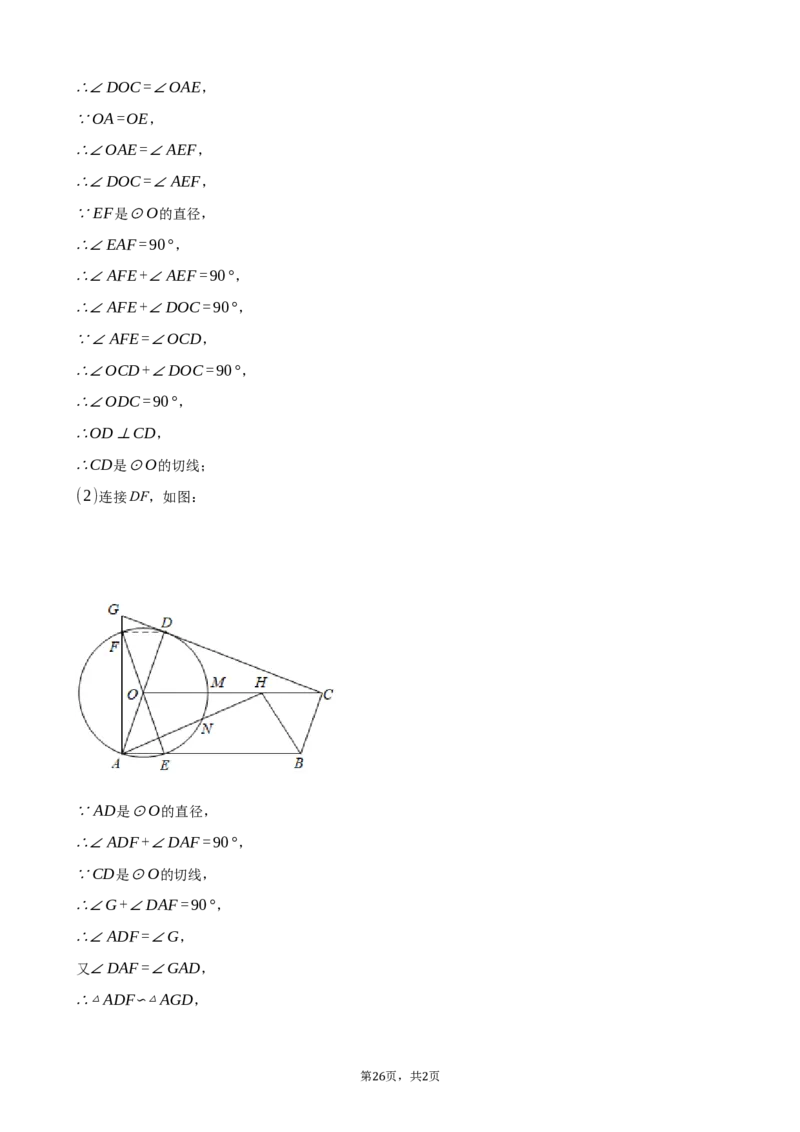
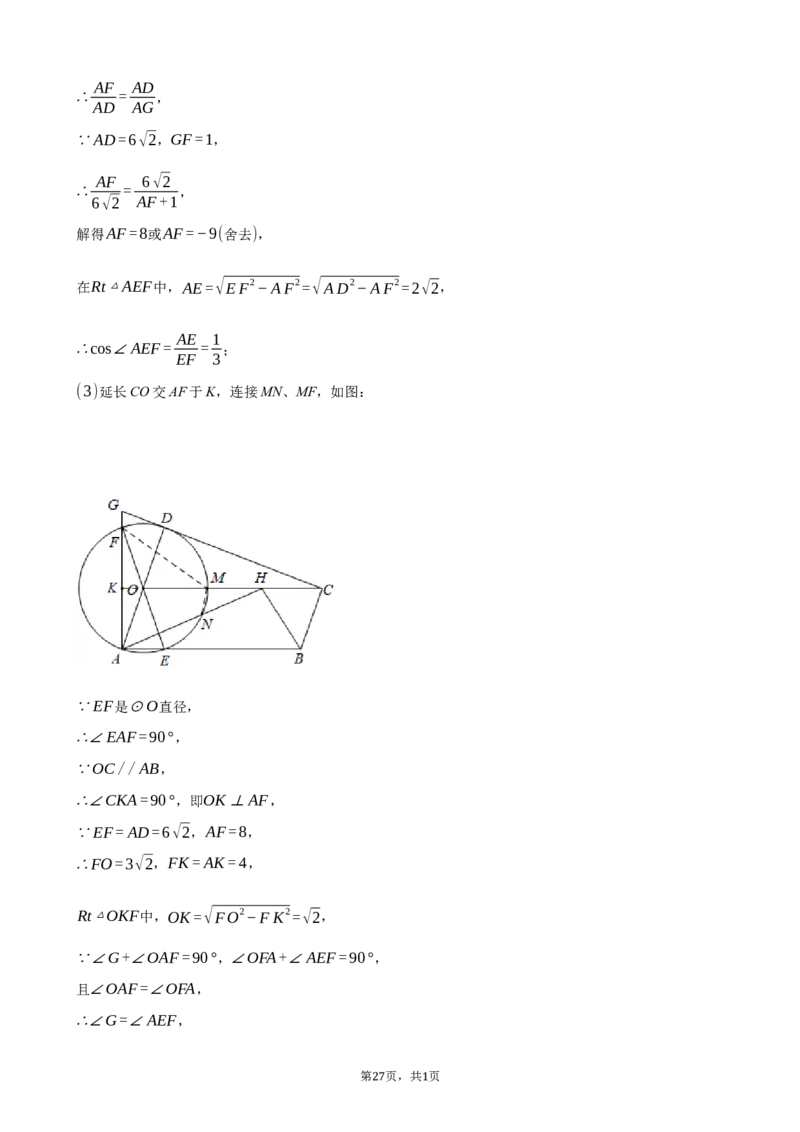
26. 如图,已知AD,EF是⊙O的直径,AD=6√2,⊙O与▱OABC的边AB,OC分别交于点E,M,连
接CD并延长,与AF的延长线交于点G,∠AFE=∠OCD.
(1)求证:CD是⊙O的切线;
(2)若GF=1,求cos∠AEF的值;
AB
(3)在(2)的条件下,若∠ABC的平分线BH交CO于点H,连接AH交⊙O于点N,求 的值.
NH
第 页,共 页
9 1第 页,共 页
10 2答案和解析
1.【答案】D
【解析】解:0是有理数.
故选:D.
根据有理数的定义,可得答案.
本题考查了实数,无理数是无限不循环小数,有理数是有限小数或无限不循环小数.
2.【答案】C
【解析】解:由该几何体的主视图可知,该几何体是 .
故选:C.
主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.依题意,该几何体的主视
图为上下两个梯形,易判断该几何体是上下两个圆台组成.
本题考查了由三视图判断几何体,考查学生对三视图掌握程度和灵活运用能力,同时也考查了空间想象
能力.
3.【答案】B
【解析】解:画树状图如下:
由树状图知,共有6种等可能结果,其中从C出口出来的有2种结果,
2 1
所以恰好在C出口出来的概率为 = ,
6 3
第 页,共 页
11 1故选:B.
画树状图,共有6种等可能结果,其中从C出口出来的有2种结果,再由概率公式求解即可.
此题考查的是列表法或树状图法求概率以及概率公式.列表法可以不重复不遗漏的列出所有可能的结果,
适合于两步完成的事件;树状图法适合两步或两步以上完成的事件.
4.【答案】C
【解析】解:400000000=4×108,
故选:C.
科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a
时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.
此题考查科学记数法的表示方法,关键是确定a的值以及n的值.
5.【答案】A
【解析】解:从图象可以看出,这一天中的最高气温是大概14时是8℃,最低气温是−4℃,从0时至
4时,这天的气温在逐渐降低,从4时至8时,这天的气温在逐渐升高,
故A正确,B,D错误;
这一天中最高气温与最低气温的差为12℃,
故C错误;
故选:A.
根据该市一天内的气温变化图,分析变化趋势和具体数值,即可求出答案.
本题考查了函数的图象,认真观察函数的图象,从图象中得到必要的信息是解决问题的关键.
6.【答案】A
【解析】解:A.a2 ⋅a3=a5,故此选项符合题意;
B.(a2
)
3=a6,故此选项不合题意;
C.a6÷a2=a4,故此选项不合题意;
D.3a2−2a,不是同类项,无法合并,故此选项不合题意.
故选:A.
直接利用合并同类项法则以及幂的乘方运算法则、同底数幂的乘法除法运算法则计算得出答案.
此题主要考查了合并同类项以及幂的乘方运算、同底数幂的乘法除法运算法则,正确掌握相关运算法则
第 页,共 页
12 2是解题关键.
7.【答案】B
【解析】解:点P(3,4)关于中心对称的点的坐标为(−3,−4).
故选:B.
平面直角坐标系中任意一点P(x,y),关于原点的对称点是(−x,−y),记忆方法是结合平面直角坐标系
的图形记忆.
此题主要考查了关于原点对称的点的坐标,正确记忆横纵坐标的符号关系是解题关键.
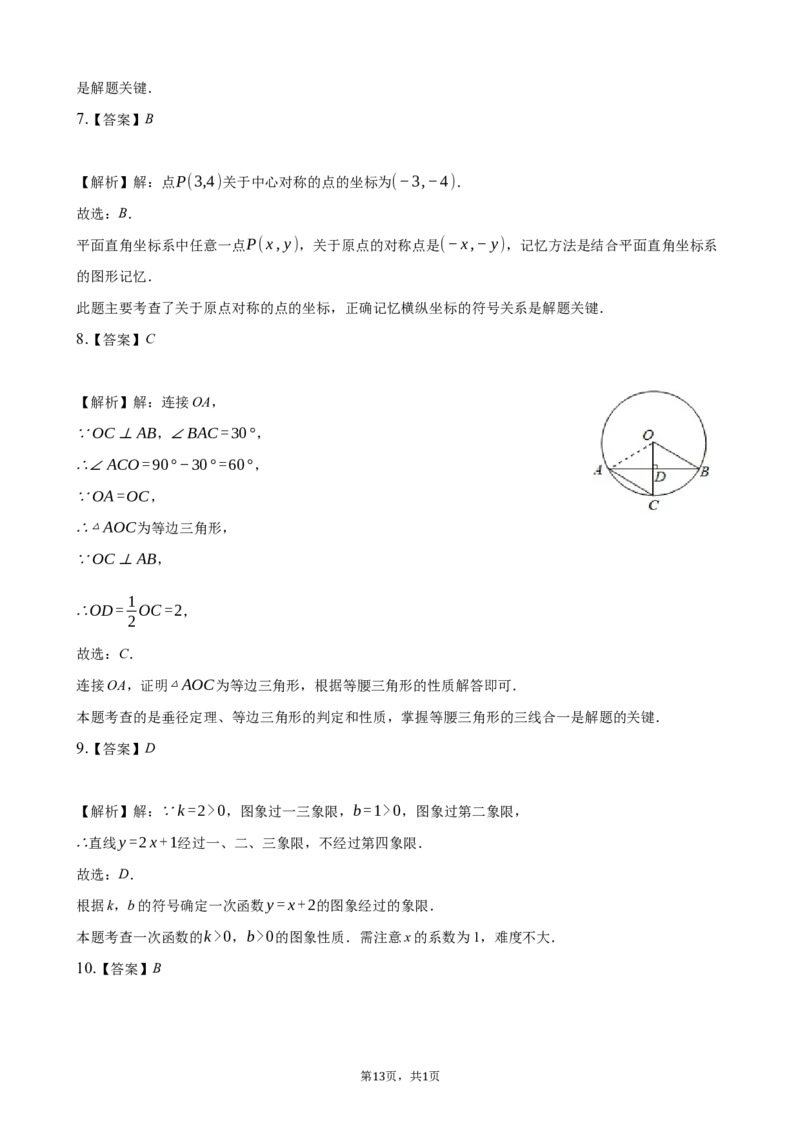
8.【答案】C
【解析】解:连接OA,
∵OC⊥AB,∠BAC=30°,
∴∠ACO=90°−30°=60°,
∵OA=OC,
∴△AOC为等边三角形,
∵OC⊥AB,
1
∴OD= OC=2,
2
故选:C.
连接OA,证明△AOC为等边三角形,根据等腰三角形的性质解答即可.
本题考查的是垂径定理、等边三角形的判定和性质,掌握等腰三角形的三线合一是解题的关键.
9.【答案】D
【解析】解:∵k=2>0,图象过一三象限,b=1>0,图象过第二象限,
∴直线y=2x+1经过一、二、三象限,不经过第四象限.
故选:D.
根据k,b的符号确定一次函数y=x+2的图象经过的象限.
本题考查一次函数的k>0,b>0的图象性质.需注意x的系数为1,难度不大.
10.【答案】B
第 页,共 页
13 1【解析】解:设共有y人,x辆车,
{y=3(x−2)
依题意得: .
y=2x+9
故选:B.
设共有x人,y辆车,根据“如果每3人坐一辆车,那么有2辆空车;如果每2人坐一辆车,那么有9人
需要步行”,即可得出关于x,y的二元一次方程组,此题得解.
本题考查了由实际问题抽象出二元一次方程组以及数学常识,找准等量关系,正确列出二元一次方程组
是解题的关键.
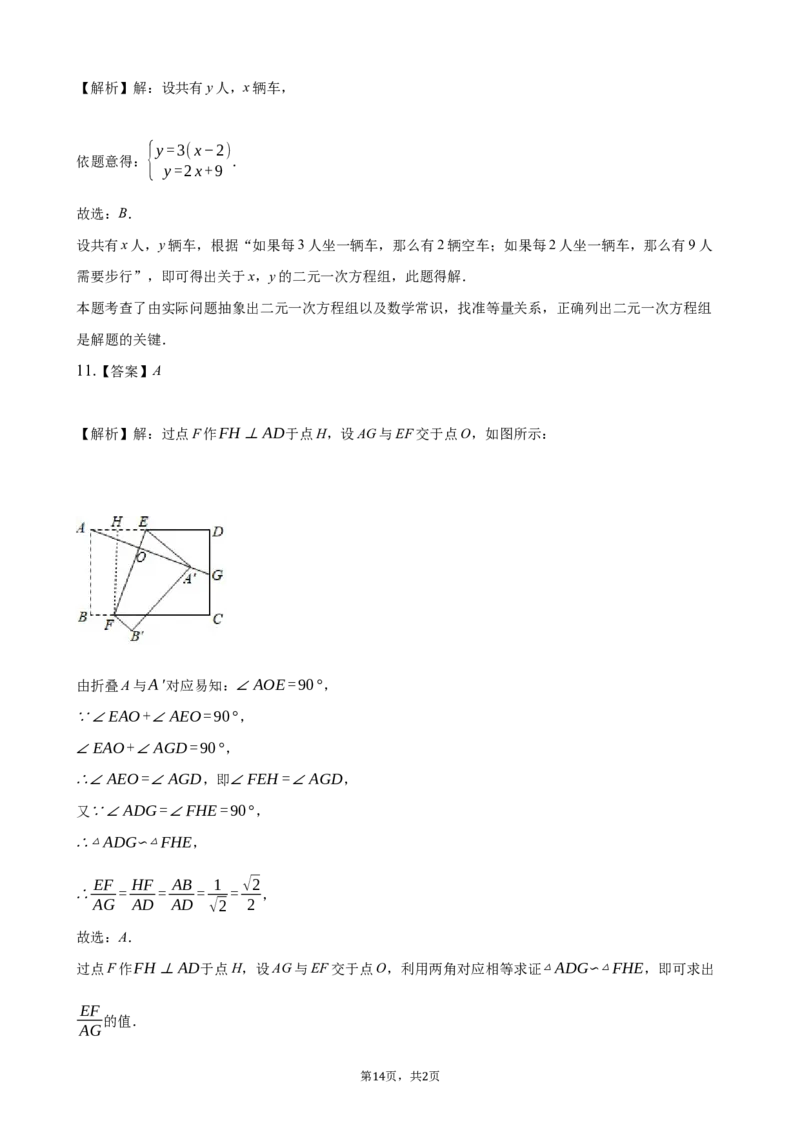
11.【答案】A
【解析】解:过点F作FH⊥AD于点H,设AG与EF交于点O,如图所示:
由折叠A与A′对应易知:∠AOE=90°,
∵∠EAO+∠AEO=90°,
∠EAO+∠AGD=90°,
∴∠AEO=∠AGD,即∠FEH=∠AGD,
又∵∠ADG=∠FHE=90°,
∴△ADG △FHE,
∽
EF HF AB 1 √2
∴ = = = = ,
AG AD AD √2 2
故选:A.
过点F作FH⊥AD于点H,设AG与EF交于点O,利用两角对应相等求证△ADG △FHE,即可求出
∽
EF
的值.
AG
第 页,共 页
14 2本题考查翻折变换,矩形性质以及相似三角形判定与性质,本题通过翻折变换推出∠AOE=90°进而利
用角进行转化求出△ADG △FHE是解题的关键.
12.【答案】C ∽
{2x+1≥2−x {2x+1<2−x
【解析】解:由新定义得 或 ,
2x+1>3 2−x>3
解得x>1或x<−1
故选:C.
分x+1≥2和x+1<2两种情况,根据新定义列出不等式组分别求解可得.
此题考查的是一元一次不等式组的解法,求不等式组的解集,应遵循以下原则:同大取较大,同小取较
小,小大大小中间找,大大小小解不了.
13.【答案】x≠2
1
【解析】解:当分母x−2≠0,即x≠2时,分式 有意义.
x−2
故答案为:x≠2.
分式有意义,则分母x−2≠0,由此易求x的取值范围.
本题考查了分式有意义的条件.从以下三个方面透彻理解分式的概念:
(1)分式无意义⇔分母为零;
(2)分式有意义⇔分母不为零;
(3)分式值为零⇔分子为零且分母不为零.
14.【答案】(a+2b)(a−2b)
【解析】解:a2−4b2=(a+2b)(a−2b).
故答案为:(a+2b)(a−2b).
直接用平方差公式进行分解.平方差公式:a2−b2=(a+b)(a−b).
本题考查运用平方差公式进行因式分解,熟记公式结构是解题的关键.
15.【答案】(30−10√3)
第 页,共 页
15 1【解析】解:由题意可得,∠ADB=60°,∠ACB=45°,AB=30m,
在Rt△ABC中,
∵∠ACB=45°,
∴AB=BC,
在Rt△ABD中,
∵∠ADB=60°,
√3
∴BD= AB=10√3(m),
3
∴CD=BC−BD=(30−10√3)m,
故答案为:(30−10√3).
在两个直角三角形中,利用特殊锐角的三角函数可求出答案.
本题考查直角三角形的边角关系,掌握直角三角形的边角公式是正确解答的前提.
16.【答案】89分
【解析】解:小婷的综合成绩为84×50%+95×40%+90×10%=89(分),
故答案为:89分.
根据加权平均数的定义列式计算可得.
本题考查的是加权平均数的求法,熟练掌握加权平均数的计算公式是解题的关键.
√3
17.【答案】
3
【解析】解:连接AC、AE,如图,
∵四边形ABCD为菱形,
1 1
∴∠BAC= ∠BAD= ×120°=60°,AB=AC,
2 2
∴△ABC为等边三角形,
∵圆弧与BC相切于E,
∴AE⊥BC,
∴BE=CE=1,
∴AE=√AB2−BE2=√22−12=√3,
第 页,共 页
16 2设圆锥的底面圆半径为r,
120×π×√3 √3
根据题意得2πr= ,解得r= ,
180 3
√3
即圆锥的底面圆半径为 .
3
√3
故答案为 .
3
连接AC、AE,如图,利用菱形的性质得到∠BAC=60°,AB=AC,则可判断△ABC为等边三角形,
再根据切线的性质得AE⊥BC,所以BE=CE=1,利用勾股定理计算出AE=√3,设圆锥的底面圆半径
120×π×√3
为r,由于圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,所以2πr= ,
180
然后解方程即可.
本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了菱形的性质和圆锥的计算.
25
18.【答案】y=(x− ) 2
13
【解析】解:过C、D作x轴平行线,作B关于直线y=4的对称点B′,过B′作B′E//CD,且
B′E=CD,连接AE交直线y=9于C′,过C′作C′D′//CD,交直线y=4于D′,如图:
第 页,共 页
17 1作图可知:四边形B′ECD和四边形C′D′DC是平行四边形,
∴B′E//CD,C′D′//CD,且B′E=DP,C′D′=CD,
∴C′D′//B′E且C′D′=B′E,
∴四边形B′EC′D′是平行四边形,
∴B′D′=EC′,
∵B关于直线y=4的对称点B′,
∴BD′=B′D′,
∴EC′=BD′,
∴AE=AC′+EC′=AC′+BD′,即此时AC′+BD′转化到一条直线上,AC′+BD′最小,最小值为AE
的长度,
而AB、CD为定值,
∴此时四边形ABC′D′的周长最小,
∵B(3,0)关于直线y=4的对称点B′,
∴B′(3,8),
∵四边形B′ECD是平行四边形,C(−3,9),D(2,4),
∴E(−2,13),
{ 0=k+b
设直线AE解析式为y=kx+b,则 ,
13=−2k+b
第 页,共 页
18 213
{k=−
3
解得 ,
13
b=
3
13 13
∴直线AE解析式为y=− x+ ,
3 3
13 13
令y=9得9=− x+ ,
3 3
14
∴x=− ,
13
14
∴C′(− ,9),
13
14 25
∴CC′=− −(−3)= ,
13 13
25
即将抛物线y=x2向右移 个单位后,四边形ABC′D′的周长最小,
13
25
∴此时抛物线为y=(x− ) 2 ,
13
25
故答案为:y=(x− ) 2 .
13
过C、D作x轴平行线,作B关于直线y=4的对称点B′,过B′作B′E//CD,且B′E=CD,连接AE
交直线y=9于C′,过C′作C′D′//CD,交直线y=4于D′,四边形B′ECD和四边形C′D′DC是平行
四边形,可得四边形B′EC′D′是平行四边形,可证AE=AC′+EC′=AC′+BD′,AC′+BD′最小,
最小值为AE的长度,故此时四边形ABC′D′的周长最小,求出B′(3,8),E(−2,13),可得直线AE解
13 13 14 14 25 25
析式为y=− x+ ,从而C′(− ,9),CC′=− −(−3)= ,故将抛物线y=x2向右移 个单
3 3 13 13 13 13
位后,四边形ABC′D′的周长最小,即可得到答案.
本题考查二次函数背景下的平移、对称变换,解题的关键是作出图形,求到C′的坐标.
1
19.【答案】解:原式=8× ÷(−2)
2
=4÷(−2)
第 页,共 页
19 1=−2.
【解析】原式先计算乘方运算,再计算乘除运算,最后算加减运算即可求出值.
此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.
20.【答案】解:去分母得:3x=x+3x+3,
解得:x=−3,
检验:当x=−3时,3(x+1)≠0,
∴分式方程的解为x=−3.
【解析】分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
此题考查了解分式方程,利用了转化的思想,解分式方程注意要检验.
21.【答案】(1)证明:∵AB//CD,
∴∠ACD=∠CAB,
在△ABC和△CDA中,
{
∠B=∠D
∠CAB=∠ACD,
AC=CA
∴△ABC △CDA(AAS);
(2)解:过≌点C作AB的垂线,垂足为E,如图:
(3)解:由(1)知:△ABC △CDA,
∵四边形ABCD的面积为2≌0,
∴S =S =10,
△ABC △CDA
第 页,共 页
20 21
∴ AB⋅CE=10,
2
∵AB=5,
∴CE=4.
【解析】(1)由AB//CD得∠ACD=∠CAB,结合∠B=∠D,AC=CA,即可根据AAS证明△ABC
△CDA;
≌
1
(2)以C为圆心,CB为半径作弧,交线段AB延长线于F,分别以B、F为圆心,大于 BF的线段长为半
2
径作弧,两弧交于G、H,连接GH,交AF于E,作直线CE,则CE即为AB的垂线;
1
(3)由△ABC △CDA,四边形ABCD的面积为20,可得S =S =10,即可列出 AB⋅CE=10,
△ABC △CDA 2
≌
而AB=5,即得CE=4.
本题考查全等三角形的判定和性质,涉及尺规作图、三角形面积等知识,解题的关键是掌握过一点作已
知直线的垂线的方法:即是作线段BF的垂直平分线.
22.【答案】解:(1)a=20−2−1−7−3−1=6,
分析数据:样本中,4.7出现的次数最多;故众数b为4.7,
4.7+4.8
将数据从小到大排列,找最中间的两个数为4.7,4.8,故中位数c= =4.75,
2
∴a=6,b=4.7,c=4.75;
(2)选择平均数4.7,
这2000箱荔枝共损坏了2000×(5−4.7)=600(千克);
(3)10×2000×5÷(2000×5−600)≈10.7(元),
答:该公司销售这批荔枝每千克定为10.7元才不亏本.
【解析】(1)根据题意以及众数、中位数的定义分别求出即可;
(2)从平均数、中位数、众数中,任选一个计算即可;
(3)求出成本,根据(2)的结果计算即可得到答案.
本题考查的是平均数、众数和中位数的定义及运用.要学会根据统计量的意义分析解决问题.
23.【答案】解:【类比探究】过点E作EF⊥CD于点F,连接AF,
∵四边形ABCD是正方形,
第 页,共 页
21 1∴AD=CD=4,∠ADC=90°,
∵DE=CE,EF⊥CD,
1
∴DF=CF= CD=2,∠ADC=∠EFD=90°,
2
∴AD//EF,
∴S =S ,
△ADE △ADF
1 1
∴S = ×AD×DF= ×4×2=4;
△ADE 2 2
【拓展应用】如图③,连接CF,
∵四边形ABCD和四边形CGFE都是正方形,
∴∠BDC=45°,∠GCF=45°,
∴∠BDC=∠GCF,
∴BD//CF,
∴S =S ,
△BDF △BCD
1
∴S = BC×BC=8.
△BDF 2
1
【解析】【类比探究】由等腰三角形的性质可得DF=CF= CD=2,∠ADC=∠EFD=90°,可证
2
AD//EF,可得S =S ,由三角形的面积公式可求解;
△ADE △ADF
【拓展应用】连接CF,由正方形的性质可得∠BDC=∠GCF,可得BD//CF,可得S =S ,
△BDF △BCD
由三角形的面积公式可求解.
本题是四边形综合题,考查了正方形的性质,等腰三角形的性质,三角形面积公式等知识,能掌握和运
用“阅读理解”中的知识是解题的关键.
第 页,共 页
22 21
24.【答案】解:(1)由题意可知抛物线C :y=− x2+bx+c过点(0,4)和(4,8),将其代入得:
2 8
{ 4=c { 3
b=
1 ,解得: 2,
8=− ×42+4b+c
8 c=4
1 3
∴抛物线C 的函数解析式为:y=− x2+ x+4;
2 8 2
(2)设运动员运动的水平距离为m米时,运动员与小山坡的竖直距离为1米,依题意得:
1 3 1 7
− m2+ m+4−(− m2+ m+1)=1,
8 2 12 6
整理得:(m−12)(m+4)=0,
解得:m =12,m =−4(舍去),
1 2
故运动员运动的水平距离为12米时,运动员与小山坡的竖直距离为1米;
1 7 1 61
(3)C :y=− x2+ x+1=− (x−7) 2+ ,
1 12 6 12 12
当x=7时,运动员到达坡顶,
1 61
即− ×72+7b+4>3+ ,
8 12
35
解得:b> .
24
1
【解析】(1)根据题意将点(0,4)和(4,8)代入C :y=− x2+bx+c求出b、c的值即可写出C 的函数解
2 8 2
析式;
(2)设运动员运动的水平距离为m米时,运动员与小山坡的竖直距离为1米,依题意得:
1 3 1 7
− m2+ m+4−(− m2+ m+1)=1,解出m即可;
8 2 12 6
61 1 61
(3)求出山坡的顶点坐标为(7, ),根据题意即− ×72+7b+4>3+ ,再解出b的取值范围即可.
12 8 12
本题考查二次函数的基本性质及其应用,熟练掌握二次函数的基本性质,并能将实际问题与二次函数模
型相结合是解决本题的关键.
第 页,共 页
23 125.【答案】解:(1)设EF=m.
∵BC=14,BD=6,
∴CD=BC−BD=14−6=8,
∵AD=8,
∴AD=DC=8,
∵AD⊥BC,
∴∠ADC=90°,
∴AC=√2AD=8√2,
∵四边形EFGH是正方形,
∴EH=FG=GH=EF=m,∠EHG=∠FGH=90°,
∴∠AHE=∠FGC=90°,
∵∠DAC=∠C=45°,
∴∠AEH=∠EAH=45°,∠GFC=∠C=45°,
∴AH=EH=x,CG=FG=x,
∴3m=8√2,
8√2
∴m= ,
3
8√2
∴EF= .
3
(2)∵DE=DF=x,DA=DC=8,
∴AE=CF=8−x,
√2 √2
∴EH= AE= (8−x),EF=√2DE=√2x,
2 2
1
×(8−x)×6
S 2 3
∴y= 1= = ,
S √2 x
2 √2x× (8−x)
2
3√2
∴y= (0