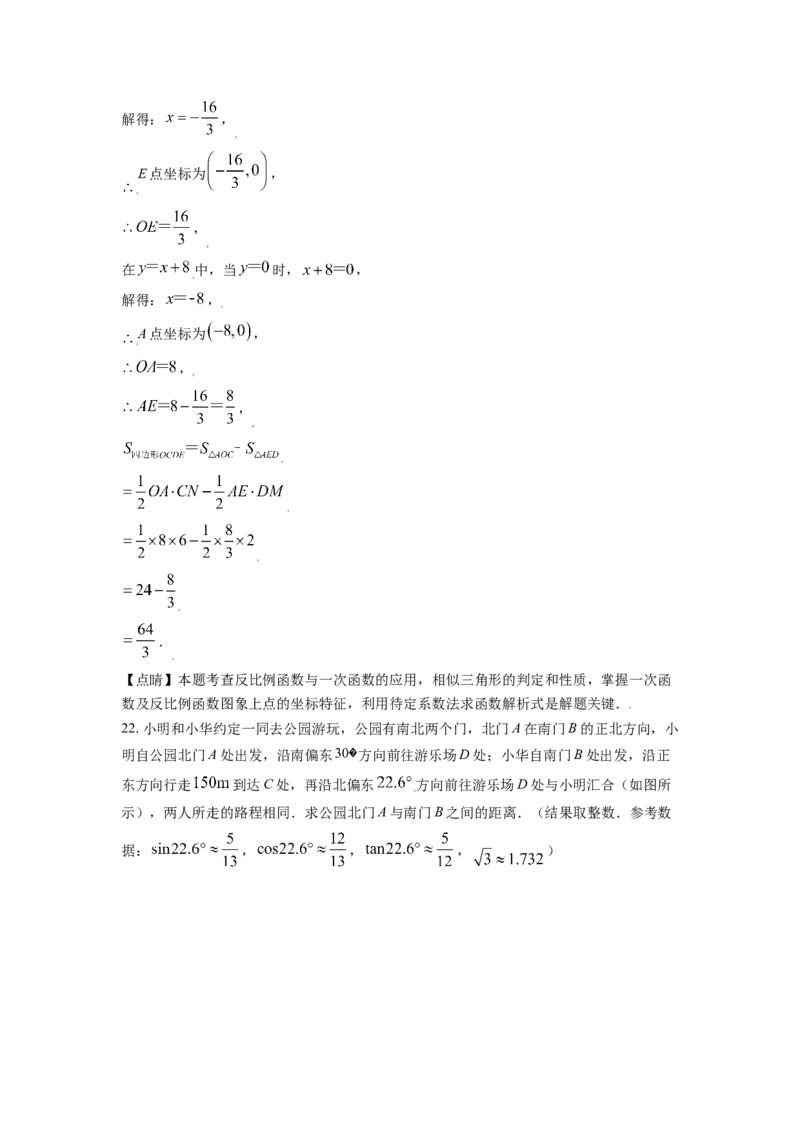文档内容
2021 年辽宁省鞍山市中考数学试卷
一、选择题(下列各题的备选答案中,只有一个是正确的每小题3分,共24
分)
1. 下列实数最小的是( )
A. -2 B. -3.5 C. 0 D. 1
【答案】B
【解析】
【分析】根据实数大小比较的方法进行求解即可.
【详解】解:因 为,
所以最小的实数是-3.5.
故选:B.
【点睛】本题主要考查了实数的大小比较,熟练掌握应用实数大小的比较方法进行求解是
解题的关键.
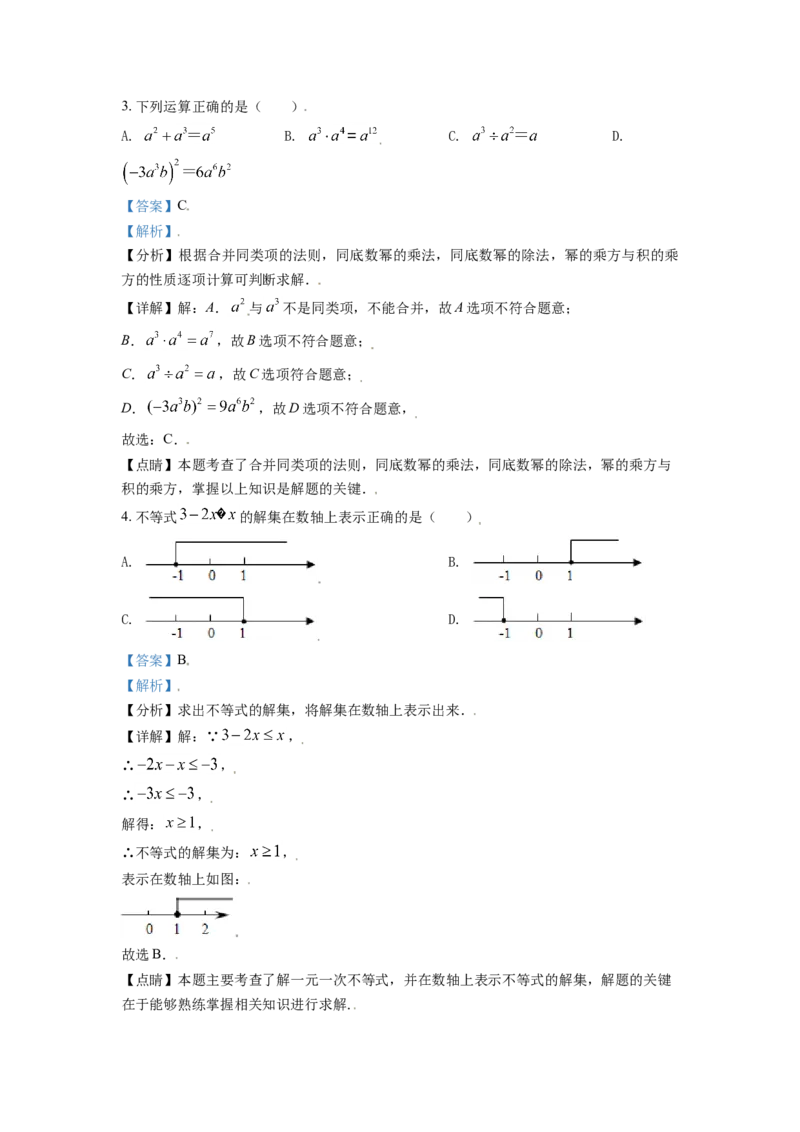
2. 下列四幅图片上呈现 的是垃圾类型及标识图案,其中标识图案是中心对称图形的是(
)
A. B. C. D.
【答案】D
【解析】
【分析】把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那
么这个图形就叫做中心对称图形.据此判断即可.
【详解】解:A.不是中心对称图形,故本选项不合题意;
B.不是中心对称图形,故本选项不合题意;
C.不是中心对称图形,故本选项符合题意;
D.是中心对称图形,故本选项符合题意.
故选D.
【点睛】本题主要考查了中心对称图形的概念,掌握中心对称图形的概念是解答本题的关
键.3. 下列运算正确的是( )
A. B. C. D.
【答案】C
【解析】
【分析】根据合并同类项的法则,同底数幂的乘法,同底数幂的除法,幂的乘方与积的乘
方的性质逐项计算可判断求解.
【详解】解:A. 与 不是同类项,不能合并,故A选项不符合题意;
B. ,故B选项不符合题意;
C. ,故C选项符合题意;
D. ,故D选项不符合题意,
故选:C.
【点睛】本题考查了合并同类项的法则,同底数幂的乘法,同底数幂的除法,幂的乘方与
积的乘方,掌握以上知识是解题的关键.
4. 不等式 的解集在数轴上表示正确的是( )
A. B.
C. D.
【答案】B
【解析】
【分析】求出不等式的解集,将解集在数轴上表示出来.
【详解】解:∵ ,
∴ ,
∴ ,
解得: ,
∴不等式的解集为: ,
表示在数轴上如图:
故选B.
【点睛】本题主要考查了解一元一次不等式,并在数轴上表示不等式的解集,解题的关键
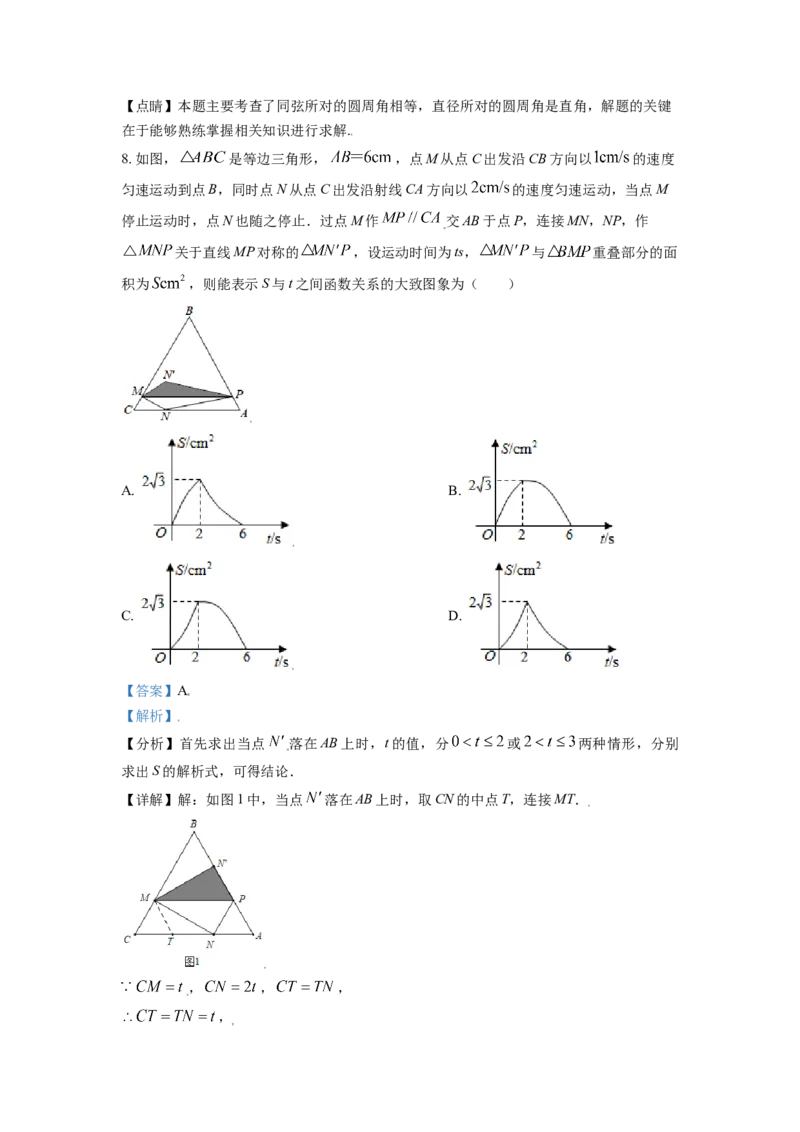
在于能够熟练掌握相关知识进行求解.5. 如图,直线 ,将一个含 角的三角尺按如图所示的位置放置,若 ,则
的度数为( )
A. B. C. D.
【答案】C
【解析】
【分析】根据平行线的性质求解,找出图中 ,进而求出∠3,再根据平行线
性质求出∠2即可.
【详解】解:如图,作 ,
三角尺是含 角的三角尺,
,
,
,
,
, ,
,
,
故选:C.
【点睛】此题考查平行线的性质,利用平行线性质求角,涉及到直角三角形两个余角的关
系.
6. 某班40名同学一周参加体育锻炼时间统计如表所示:
时间/h 6 7 8 9
人数 2 18 14 6
那么该班40名同学一周参加体育锻炼时间的众数、中位数分别是( )
A. 18,7.5 B. 18,7 C. 7,8 D. 7,7.5
【答案】D【解析】
【分析】根据众数和中位数的定义进行求解即可得出答案.
【详解】解:根据题意可得,参加体育锻炼时间的众数为7,
因为该班有40名同学,所以中位数为第20和21名同学时间,第20名同学的时间为 ,
第21名同学的时间为 ,
所以中位数为 .
故选:D.
【点睛】考查了中位数、众数的概念.本题为统计题,考查众数与中位数的意义,中位数
是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平
均数),叫做这组数据的中位数.
7. 如图,AB为 的直径,C,D为 上的两点,若 ,则 的度数为(
)
A. B. C. D.
【答案】B
【解析】
【分析】连接AD,如图,根据圆周角定理得到 , ,然后利用互
余计算出 ,从而得到 的度数.
【详解】解:连接AD,如图,
AB为 的直径,
,
,
.
故选B.【点睛】本题主要考查了同弦所对的圆周角相等,直径所对的圆周角是直角,解题的关键
在于能够熟练掌握相关知识进行求解.
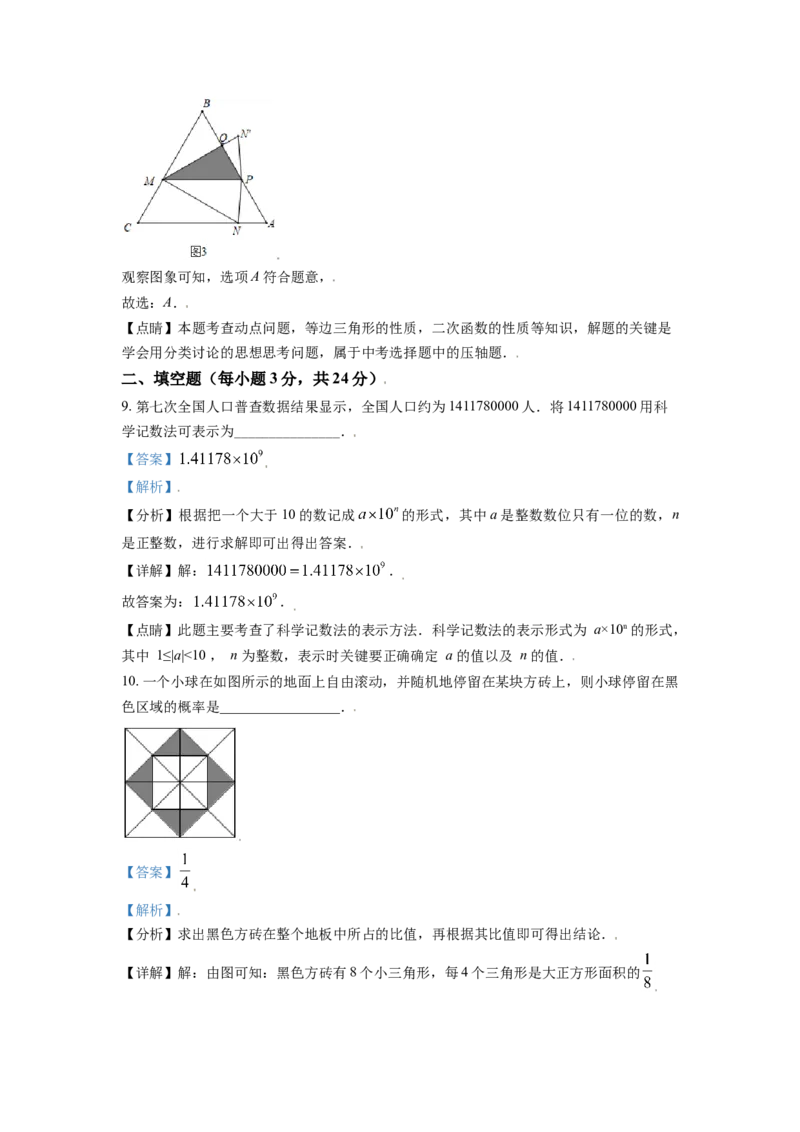
8. 如图, 是等边三角形, ,点M从点C出发沿CB方向以 的速度
匀速运动到点B,同时点N从点C出发沿射线CA方向以 的速度匀速运动,当点M
停止运动时,点N也随之停止.过点M作 交AB于点P,连接MN,NP,作
关于直线MP对称的 ,设运动时间为ts, 与 重叠部分的面
积为 ,则能表示S与t之间函数关系的大致图象为( )
A. B.
C. D.
【答案】A
【解析】
【分析】首先求出当点 落在AB上时,t的值,分 或 两种情形,分别
求出S的解析式,可得结论.
【详解】解:如图1中,当点 落在AB上时,取CN的中点T,连接MT.
, , ,
,是等边三角形,
,
是等边三角形,
,
,
,
, , ,
, 是等边三角形,
,
,
,
,
四边形CMPN是平行四边形,
,
,
,
如图2中,当 时,过点M作 于K,则 ,
.
如图3中,当 时, ,观察图象可知,选项A符合题意,
故选:A.
【点睛】本题考查动点问题,等边三角形的性质,二次函数的性质等知识,解题的关键是
学会用分类讨论的思想思考问题,属于中考选择题中的压轴题.
二、填空题(每小题3分,共24分)
9. 第七次全国人口普查数据结果显示,全国人口约为1411780000人.将1411780000用科
学记数法可表示为_______________.
【答案】
【解析】
【分析】根据把一个大于10的数记成 的形式,其中a是整数数位只有一位的数,n
是正整数,进行求解即可出得出答案.
【详解】解: .
故答案为: .
【点睛】此题主要考查了科学记数法的表示方法.科学记数法的表示形式为 a×10n 的形式,
其中 1≤|a|<10 , n 为整数,表示时关键要正确确定 a 的值以及 n 的值.
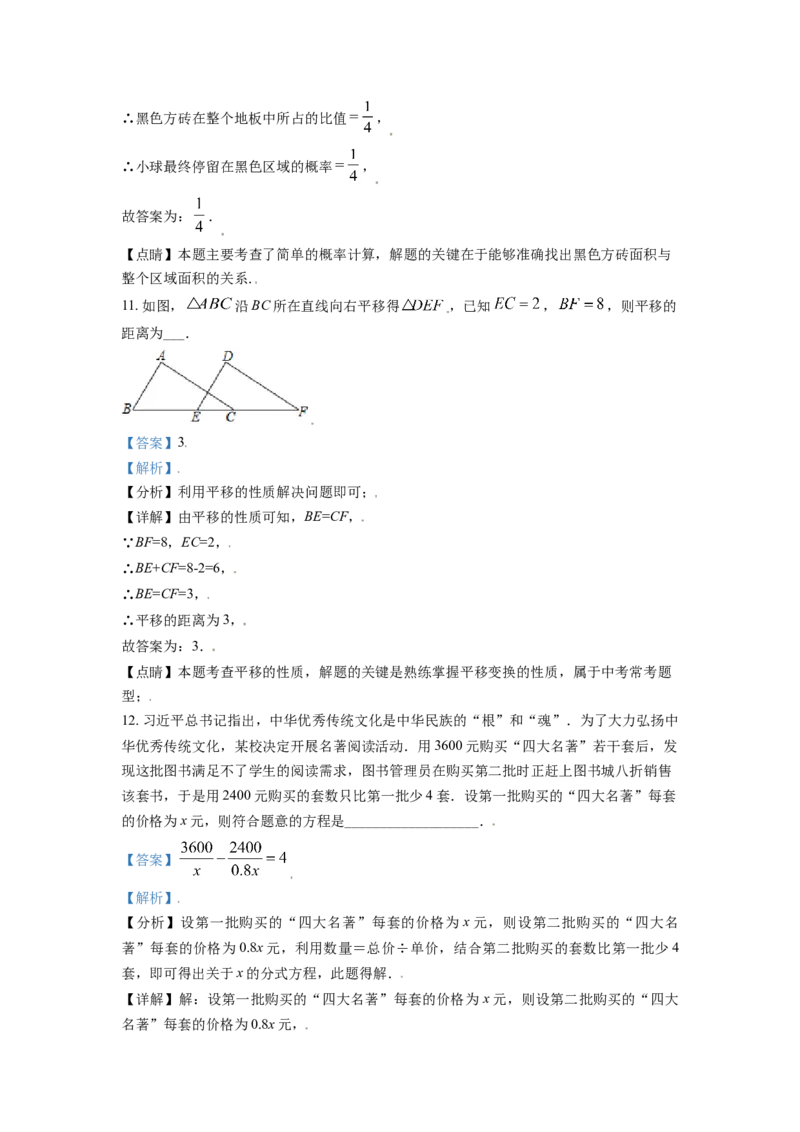
10. 一个小球在如图所示的地面上自由滚动,并随机地停留在某块方砖上,则小球停留在黑
色区域的概率是_________________.
【答案】
【解析】
【分析】求出黑色方砖在整个地板中所占的比值,再根据其比值即可得出结论.
【详解】解:由图可知:黑色方砖有8个小三角形,每4个三角形是大正方形面积的∴黑色方砖在整个地板中所占的比值 ,
∴小球最终停留在黑色区域的概率 ,
故答案为: .
【点睛】本题主要考查了简单的概率计算,解题的关键在于能够准确找出黑色方砖面积与
整个区域面积的关系.
11. 如图, 沿BC所在直线向右平移得 ,已知 , ,则平移的
距离为___.
【答案】3
【解析】
【分析】利用平移的性质解决问题即可;
【详解】由平移的性质可知,BE=CF,
∵BF=8,EC=2,
∴BE+CF=8-2=6,
∴BE=CF=3,
∴平移的距离为3,
故答案为:3.
【点睛】本题考查平移的性质,解题的关键是熟练掌握平移变换的性质,属于中考常考题
型;
12. 习近平总书记指出,中华优秀传统文化是中华民族的“根”和“魂”.为了大力弘扬中
华优秀传统文化,某校决定开展名著阅读活动.用3600元购买“四大名著”若干套后,发
现这批图书满足不了学生的阅读需求,图书管理员在购买第二批时正赶上图书城八折销售
该套书,于是用2400元购买的套数只比第一批少4套.设第一批购买的“四大名著”每套
的价格为x元,则符合题意的方程是___________________.
【答案】
【解析】
【分析】设第一批购买的“四大名著”每套的价格为 x元,则设第二批购买的“四大名
著”每套的价格为0.8x元,利用数量=总价÷单价,结合第二批购买的套数比第一批少4
套,即可得出关于x的分式方程,此题得解.
【详解】解:设第一批购买的“四大名著”每套的价格为 x元,则设第二批购买的“四大
名著”每套的价格为0.8x元,依题意得: .
故答案为: .
【点睛】本题主要考查了分式方程的实际应用,解题的关键在于能够准确找到等量关系列
出方程.
13. 如图,矩形ABCD中, ,对角线AC,BD交于点O, ,垂足为点
H,若 ,则AD的长为_______________.
【答案】
【解析】
【分析】由矩形的性质得 , ,求出 ,利用30°
角的直角三角形的性质求出 CH 的长度,再利用勾股定理求出 DH 的长度,根据
求出 ,然后由含 角的直角三角形的性质即可求解.
【详解】解: 四边形ABCD是矩形,
, ,
,
, ,
∴
在 中,
,
,
,
,
故答案为: .
【点睛】本题考查的是矩形的性质以及直角三角形30°的性质,熟练掌握直角三角形30°
的性质是解决本题的关键.
14. 如图, ,定长为a的线段端点A,B分别在射线OP,OQ上运动(点A,
B不与点O重合),C为AB的中点,作 关于直线OC对称的 , 交AB于点D,当 是等腰三角形时, 的度数为_____________.
【答案】 或
【解析】
【 分 析 】 结 合 折 叠 及 直 角 三 角 形 斜 边 中 线 等 于 斜 边 一 半 的 性 质 可 得
,设 ,然后利用三角形外角
和等腰三角形的性质表示出 , , ,
,从而利用分类讨论思想解题.
【详解】解: ,C为AB的中点,
,
, ,
又由折叠性质可得 ,
,
设 ,则 , ,
, ,
①当 时, ,
,
解得 ,
;
②当 时, ,
,方程无解,
此情况不存在;
③当 时, ,
,
解得: ,
;
综上, 的度数为 或 ,
故答案为: 或 .
【点睛】此题考查折叠及直角三角形斜边中线等于斜边一半的性质,三角形外角和等腰三角形的性质,难度一般.
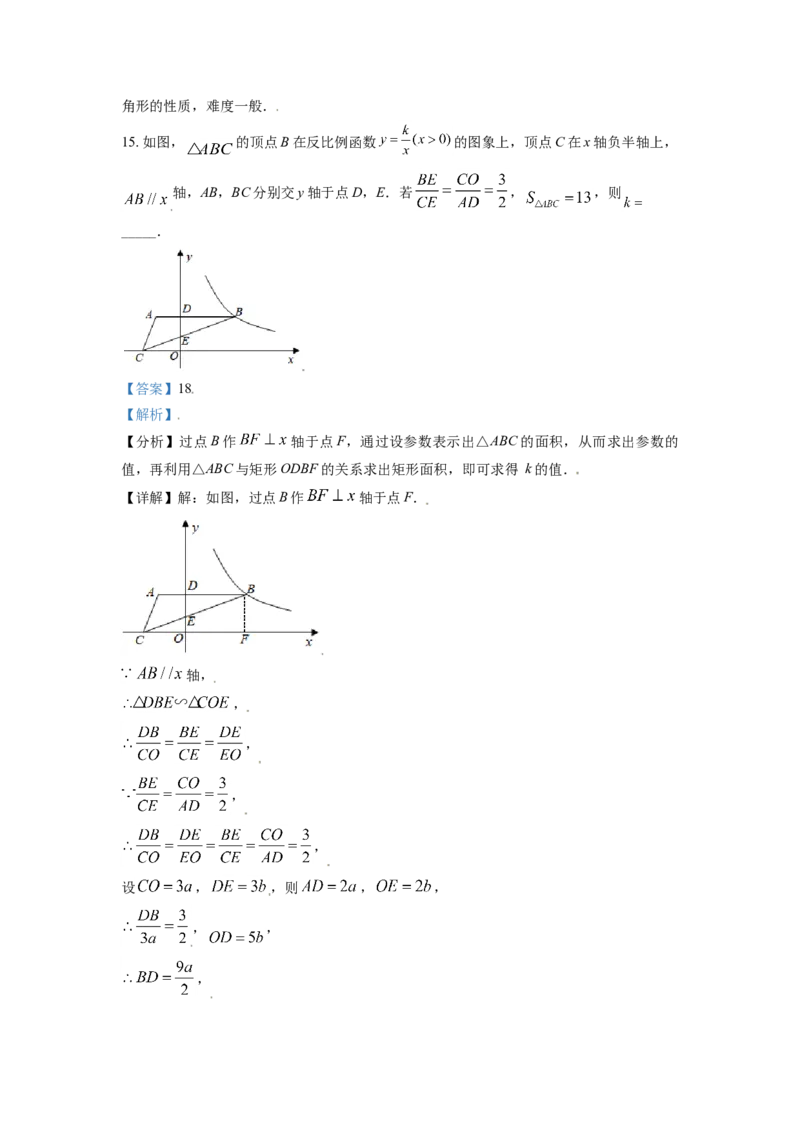
15. 如图, 的顶点B在反比例函数 的图象上,顶点C在x轴负半轴上,
轴,AB,BC分别交y轴于点D,E.若 , ,则
_____.
【答案】18
【解析】
【分析】过点B作 轴于点F,通过设参数表示出△ABC的面积,从而求出参数的
值,再利用△ABC与矩形ODBF的关系求出矩形面积,即可求得 k的值.
【详解】解:如图,过点B作 轴于点F.
轴,
,
,
,
,
设 , ,则 , ,
, ,
,,
,
,
,
又 反比例函数图象在第一象限,
,
故答案为18.
【点睛】此题考查反比例函数知识,涉及三角形相似及利用相似求长度,矩形面积公式等,
难度一般.
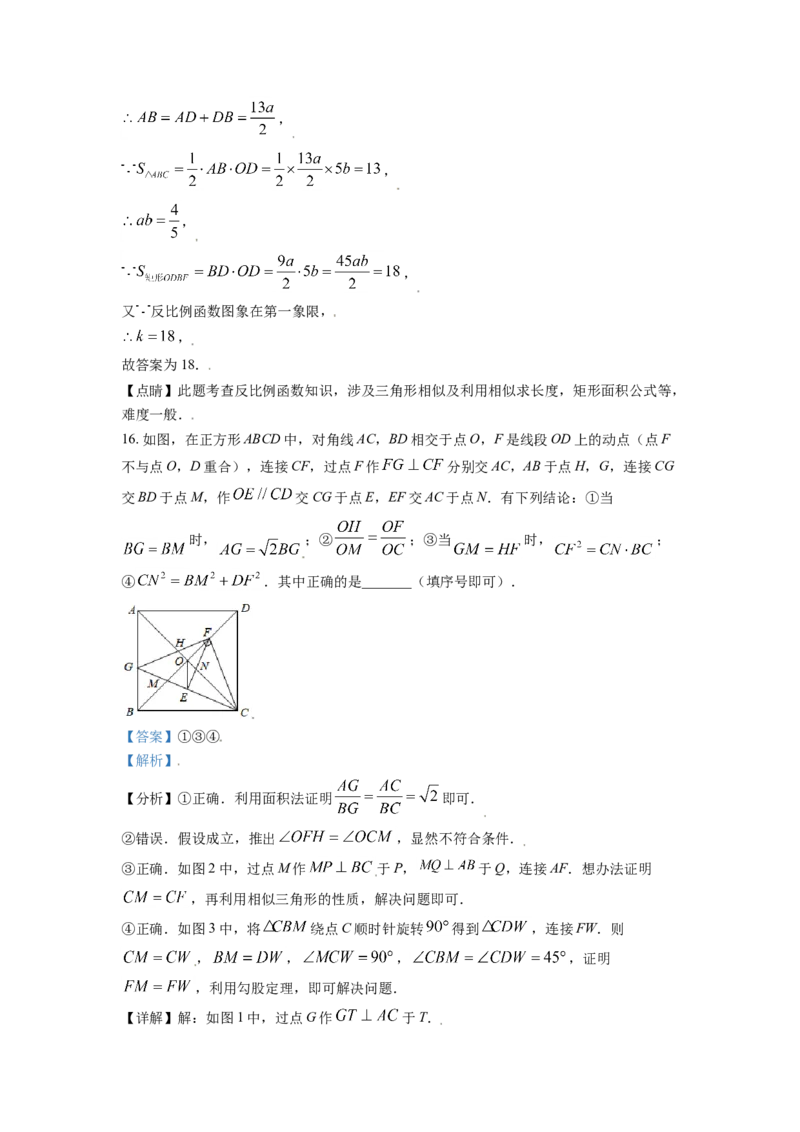
16. 如图,在正方形ABCD中,对角线AC,BD相交于点O,F是线段OD上的动点(点F
不与点O,D重合),连接CF,过点F作 分别交AC,AB于点H,G,连接CG
交BD于点M,作 交CG于点E,EF交AC于点N.有下列结论:①当
时, ;② ;③当 时, ;
④ .其中正确的是_______(填序号即可).
【答案】①③④
【解析】
【分析】①正确.利用面积法证明 即可.
②错误.假设成立,推出 ,显然不符合条件.
③正确.如图2中,过点M作 于P, 于Q,连接AF.想办法证明
,再利用相似三角形的性质,解决问题即可.
④正确.如图3中,将 绕点C顺时针旋转 得到 ,连接FW.则
, , , ,证明
,利用勾股定理,即可解决问题.
【详解】解:如图1中,过点G作 于T.,
,
, ,
四边形ABCD是正方形,
, ,
,
, ,
,
,
,故①正确,
假设 成立,
,
,
,显然这个条件不成立,故②错误,
如图2中,过点M作 于P, 于Q,连接AF.
, ,
,
, , ,
,
, ,
,
,,
,
,
,
,
,
,
,
, ,
,
,
, , ,
,
,
, ,
,
,
, ,
,
是等腰直角三角形,
,
,
,
,
,
,故③正确,如图3中,将 绕点C顺时针旋转 得到 ,连接FW.则 ,
, , ,
∵FG=FC,∠GFO=∠FCN,∠FGM=∠CFN=45°,
∴△FGM≌△CFN,
∴FM=CN,
, , ,
,
,
,
,
,故④正确,
故答案为:①③④.
【点睛】本题主要考查了相似三角形的性质与判定,全等三角形的性质与判定,等腰直角
三角形的性质,正方形的性质,旋转的性质,勾股定理等等,解题的关键在于能够熟练掌
握相关知识进行求解.
三、解答题(每小题8分,共16分)
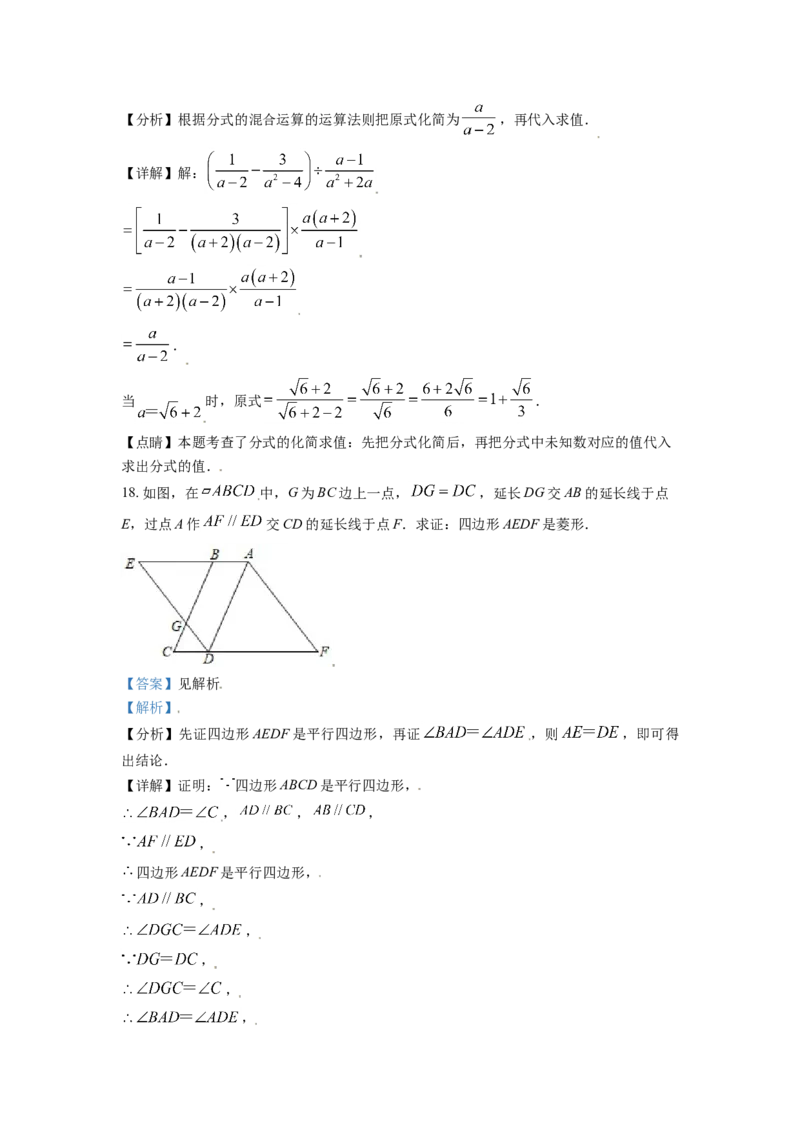
17. 先化简,再求值: ,其中 .
【答案】 ,
【解析】【分析】根据分式的混合运算的运算法则把原式化简为 ,再代入求值.
【详解】解:
.
当 时,原式 .
【点睛】本题考查了分式的化简求值:先把分式化简后,再把分式中未知数对应的值代入
求出分式的值.
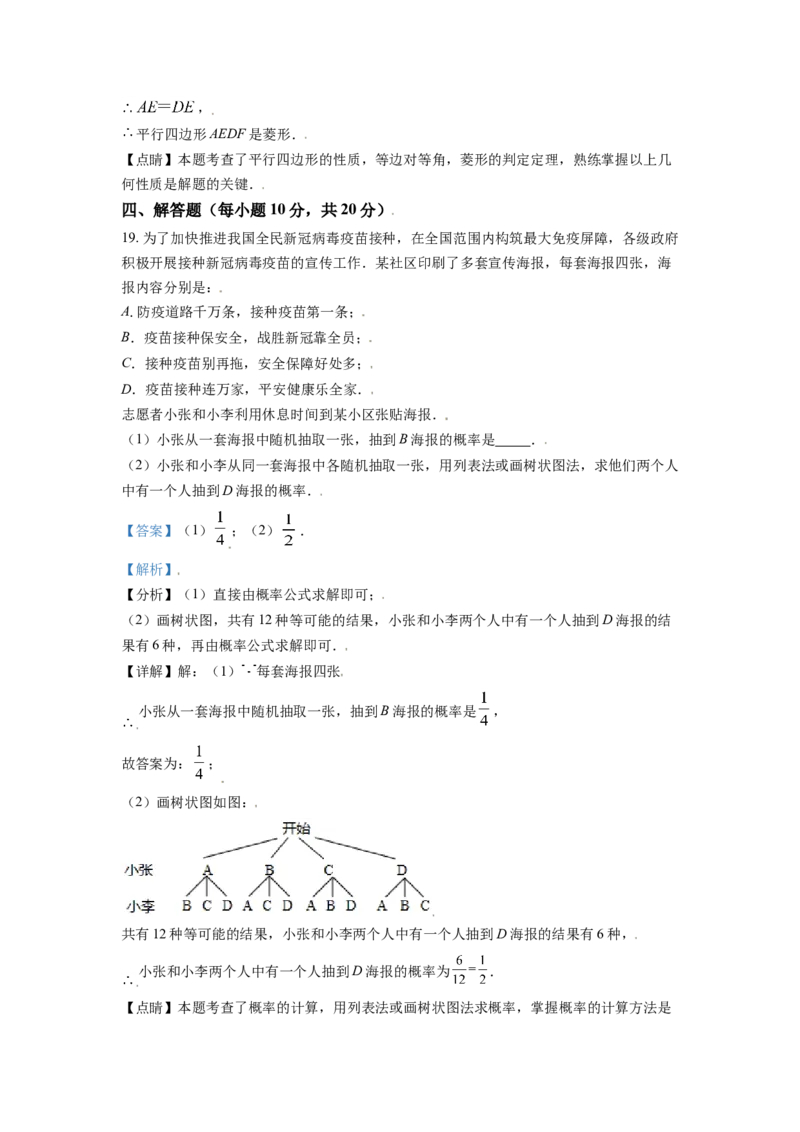
18. 如图,在 中,G为BC边上一点, ,延长DG交AB的延长线于点
E,过点A作 交CD的延长线于点F.求证:四边形AEDF是菱形.
【答案】见解析
【解析】
【分析】先证四边形AEDF是平行四边形,再证 ,则 ,即可得
出结论.
【详解】证明: 四边形ABCD是平行四边形,
, , ,
,
四边形AEDF是平行四边形,
,
,
,
,
,,
平行四边形AEDF是菱形.
【点睛】本题考查了平行四边形的性质,等边对等角,菱形的判定定理,熟练掌握以上几
何性质是解题的关键.
四、解答题(每小题10分,共20分)
19. 为了加快推进我国全民新冠病毒疫苗接种,在全国范围内构筑最大免疫屏障,各级政府
积极开展接种新冠病毒疫苗的宣传工作.某社区印刷了多套宣传海报,每套海报四张,海
报内容分别是:
A.防疫道路千万条,接种疫苗第一条;
B.疫苗接种保安全,战胜新冠靠全员;
C.接种疫苗别再拖,安全保障好处多;
D.疫苗接种连万家,平安健康乐全家.
志愿者小张和小李利用休息时间到某小区张贴海报.
(1)小张从一套海报中随机抽取一张,抽到B海报的概率是 .
(2)小张和小李从同一套海报中各随机抽取一张,用列表法或画树状图法,求他们两个人
中有一个人抽到D海报的概率.
【答案】(1) ;(2) .
【解析】
【分析】(1)直接由概率公式求解即可;
(2)画树状图,共有12种等可能的结果,小张和小李两个人中有一个人抽到D海报的结
果有6种,再由概率公式求解即可.
【详解】解:(1) 每套海报四张
小张从一套海报中随机抽取一张,抽到B海报的概率是 ,
故答案为: ;
(2)画树状图如图:
共有12种等可能的结果,小张和小李两个人中有一个人抽到D海报的结果有6种,
小张和小李两个人中有一个人抽到D海报的概率为 .
【点睛】本题考查了概率的计算,用列表法或画树状图法求概率,掌握概率的计算方法是解题的关键.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果数,概率=所
求情况数与总情况数之比.
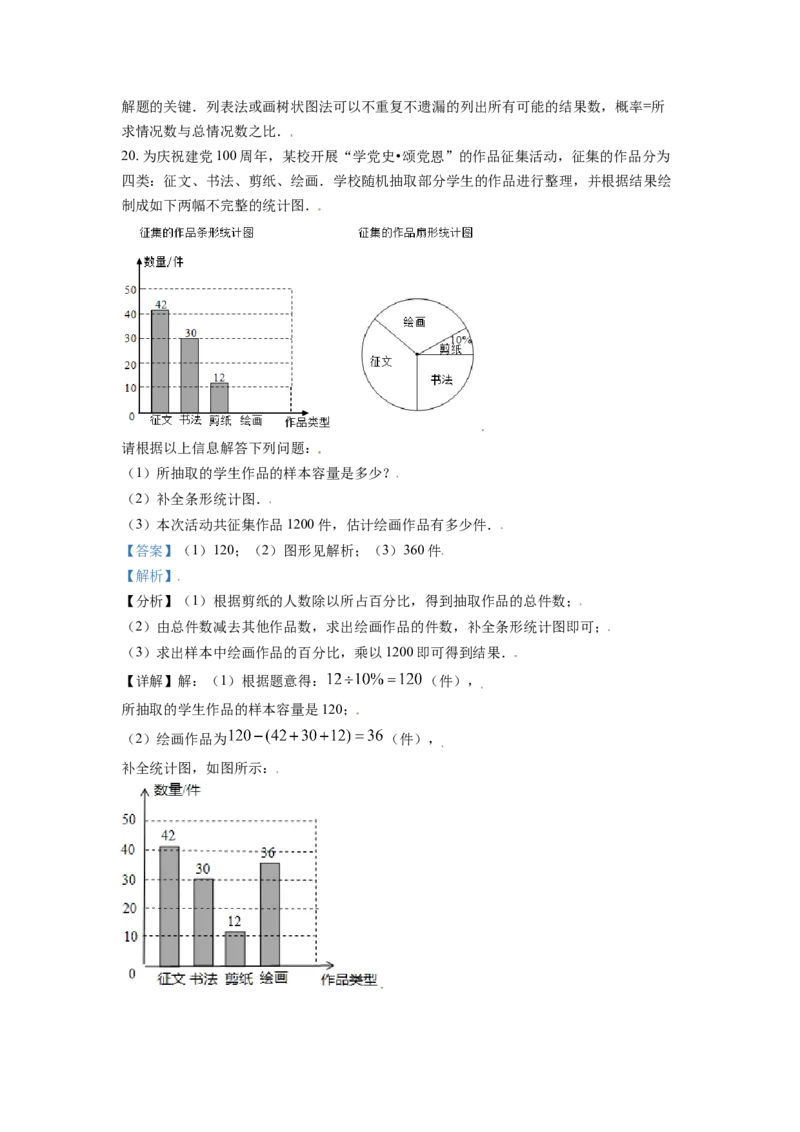
20. 为庆祝建党100周年,某校开展“学党史•颂党恩”的作品征集活动,征集的作品分为
四类:征文、书法、剪纸、绘画.学校随机抽取部分学生的作品进行整理,并根据结果绘
制成如下两幅不完整的统计图.
请根据以上信息解答下列问题:
(1)所抽取的学生作品的样本容量是多少?
(2)补全条形统计图.
(3)本次活动共征集作品1200件,估计绘画作品有多少件.
【答案】(1)120;(2)图形见解析;(3)360件
【解析】
【分析】(1)根据剪纸的人数除以所占百分比,得到抽取作品的总件数;
(2)由总件数减去其他作品数,求出绘画作品的件数,补全条形统计图即可;
(3)求出样本中绘画作品的百分比,乘以1200即可得到结果.
【详解】解:(1)根据题意得: (件),
所抽取的学生作品的样本容量是120;
(2)绘画作品为 (件),
补全统计图,如图所示:(3)根据题意得: (件),
则绘画作品约有360件.
答:本次活动共征集作品1200件时,绘画作品约有360件.
【点睛】本题主要考查了总体、个体、样本、样本容量,用样本估计总体,条形统计图和
扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关
键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分
比大小.
五、解答题(每小题10分,共20分)
21. 如图,在平面直角坐标系中,一次函数 的图象分别与x轴、y轴交于A,B
两点,与反比例函数 的图象在第二象限交于C, 两点, 交x轴
于点E,若 .
(1)求一次函数和反比例函数的表达式.
(2)求四边形OCDE的面积.
【答案】(1) , ;(2)
【解析】
【分析】(1)先利用待定系数法求反比例函数解析式,然后结合相似三角形的判定和性质
求得C点坐标,再利用待定系数法求函数关系式;
(2)根据一次函数图象上点的坐标特征并结合待定系数法求得A点和E点坐标,然后用
的面积减去 的面积求解.
【详解】解:(1)将 代入 中,
,
反比例函数的解析式为 ;
过点D作 轴,过点C作 轴,,
,
,
,
将 代入 中,
,
解得: ,
C点坐标为 ,
将 , 代入 中,
可得 ,
解得: ,
一次函数的解析式为 ;
(2)设直线OC的解析式为 ,
将 代入,得: ,
解得: ,
直线OC的解析式为 ,
由 ,设直线DE的解析式为 ,
将 代入可得: ,
解得: ,
直线DE的解析式为 ,
当 时, ,解得: ,
E点坐标为 ,
,
在 中,当 时, ,
解得: ,
A点坐标为 ,
,
,
.
【点睛】本题考查反比例函数与一次函数的应用,相似三角形的判定和性质,掌握一次函
数及反比例函数图象上点的坐标特征,利用待定系数法求函数解析式是解题关键.
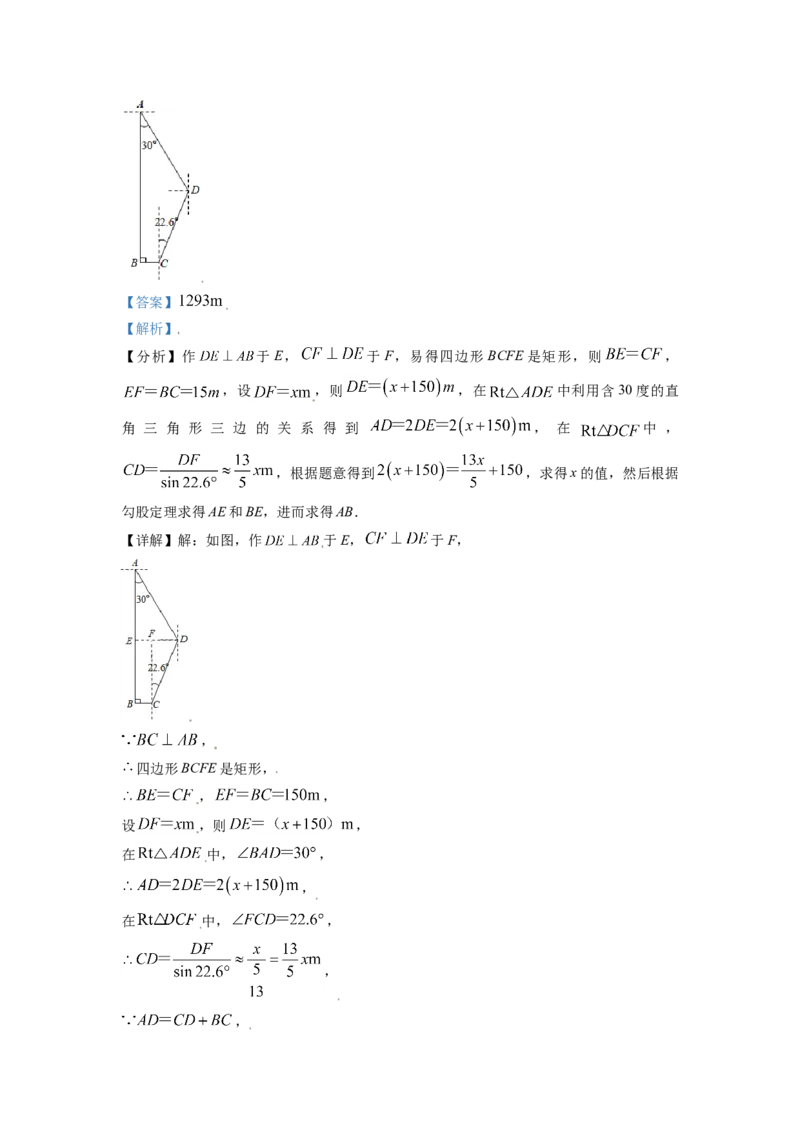
22. 小明和小华约定一同去公园游玩,公园有南北两个门,北门A在南门B的正北方向,小
明自公园北门A处出发,沿南偏东 方向前往游乐场D处;小华自南门B处出发,沿正
东方向行走 到达C处,再沿北偏东 方向前往游乐场D处与小明汇合(如图所
示),两人所走的路程相同.求公园北门A与南门B之间的距离.(结果取整数.参考数
据: , , , )【答案】
【解析】
【分析】作 于E, 于F,易得四边形 BCFE是矩形,则 ,
,设 ,则 ,在 中利用含30度的直
角 三 角 形 三 边 的 关 系 得 到 , 在 中 ,
,根据题意得到 ,求得x的值,然后根据
勾股定理求得AE和BE,进而求得AB.
【详解】解:如图,作 于E, 于F,
,
四边形BCFE是矩形,
, ,
设 ,则 ,
在 中, ,
,
在 中, ,
,
,,
解得: ,
,
,
,
,
由勾股定理得 ,
,
,
答:公园北门A与南门B之间的距离约为 .
【点睛】本题主要考查了解直角三角形的应用——方向角问题,正确构建直角三角形是解
题的关键.
六、解答题(每小题10分,共20分)
23. 如图,AB为 的直径,C为 上一点,D为AB上一点, ,过点A作
交CD的延长线于点E,CE交 于点G,连接AC,AG,在EA的延长线上取
点F,使 .
(1)求证:CF是 的切线;
(2)若 , ,求 的半径.
【答案】(1)见解析;(2)5
【解析】
【分析】(1)根据题意判定 ,然后结合相似三角形的性质求得
,从而可得 ,然后结合等腰三角形的性质求得
,从而判定CF是 的切线;
(2)由切线长定理可得 ,从而可得 ,得到 ,然后利用
勾股定理解直角三角形可求得圆的半径.【详解】(1)证明: , ,
,
,
,
,
,
又 ,
,
,
,
, ,
,
,
AB是 的直径,
,
又 ,
,
,
,
即CF是 的切线;
(2) CF是 的切线, ,
,
,
,
又 ,
在 中, ,
设 的半径为x,则 , ,
在 中, ,
解得: ,
的半径为5.【点睛】本题考查了圆周角定理、切线的判定与性质、相似三角形的判定与性质、勾股定
理等,熟练掌握相关定理与性质是解决本题的关键.
24. 2022年冬奥会即将在北京召开,某网络经销商购进了一批以冬奥会为主题的文化衫进
行销售,文化衫的进价为每件30元,当销售单价定为70元时,每天可售出20件,每销售
一件需缴纳网络平台管理费2元,为了扩大销售,增加盈利,决定采取适当的降价措施,
经调查发现:销售单价每降低1元,则每天可多售出2件(销售单价不低于进价),若设
这款文化衫的销售单价为x(元),每天的销售量为y(件).
(1)求每天的销售量y(件)与销售单价x(元)之间的函数关系式;
(2)当销售单价为多少元时,销售这款文化衫每天所获得的利润最大,最大利润为多少元?
【答案】(1) ;(2)当销售单价为56元时,每天所获得的利润最大,最
大利润为1152元
【解析】
【分析】(1)根据“销售单价每降低1元,则每天可多售出2件”列函数关系式;
(2)根据总利润=单件利润×销售量列出函数关系式,然后利用二次函数的性质分析其最
值.
【详解】解:(1)由题意可得: ,
整理,得: ,
每天的销售量y(件)与销售单价x(元)之间的函数关系式为 ;
(2)设销售所得利润为w,由题意可得:
,
整理,得: ,
,
当 时,w取最大值 为1152,
当销售单价为56元时,销售这款文化衫每天所获得的利润最大,最大利润为1152元.
【点睛】此题考查二次函数的应用——销售问题,涉及运算能力及一次函数应用,熟练掌
握相关知识是解题的关键.
七、解答题(本题满分12分)
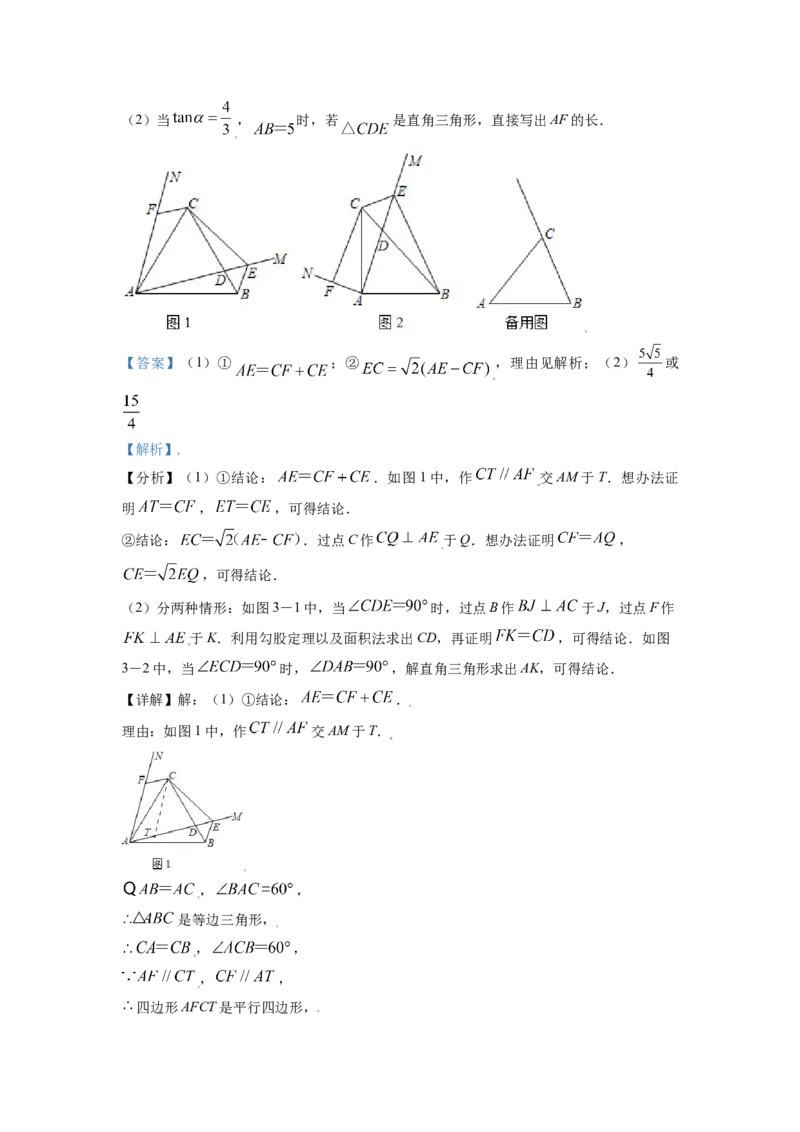
25. 如图,在 中, , ,过点A作射线AM交
射线BC于点D,将AM绕点A逆时针旋转 得到AN,过点C作 交直线AN于
点F,在AM上取点E,使 .
(1)当AM与线段BC相交时,
①如图1,当 时,线段AE,CE和CF之间的数量关系为 .
②如图2,当 时,写出线段AE,CE和CF之间的数量关系,并说明理由.(2)当 , 时,若 是直角三角形,直接写出AF的长.
【答案】(1)① ;② ,理由见解析;(2) 或
【解析】
【分析】(1)①结论: .如图1中,作 交AM于T.想办法证
明 , ,可得结论.
②结论: .过点C作 于Q.想办法证明 ,
,可得结论.
(2)分两种情形:如图3-1中,当 时,过点B作 于J,过点F作
于K.利用勾股定理以及面积法求出CD,再证明 ,可得结论.如图
3-2中,当 时, ,解直角三角形求出AK,可得结论.
【详解】解:(1)①结论: .
理由:如图1中,作 交AM于T.
, ,
是等边三角形,
, ,
, ,
四边形AFCT是平行四边形,,
, ,
,
,
,
,
,
,
,
,
是等边三角形,
,
.
故答案为: .
②如图2中,结论: .
理由:过点C作 于Q.
,
,
,
,
,
四边形AFCQ是矩形,
,
, ,
,,
,
,
,
,
,
,
,
.
(2)如图3-1中,当 时,过点B作 于J,过点F作 于
K.
在 中, , ,
, ,
,
,
,
,
,
,
,
,
,,
四边形CDKF是平行四边形,
,
四边形CDKF是矩形,
,
,
,
,
.
如图3-2中,当 时,同理可得:
,
,
,
在 中, , ,
, ,
,
,
, ,
,,
,
.
综上所述,满足条件的AF的值为 或 .
【点睛】此题是几何变换综合题.考查了等边三角形的判定及性质,平行四边形的判定及
性质,相似三角形的判定及性质,勾股定理,锐角三角函数,此题是一道几何综合题,掌
握各知识点并掌握推理能力是解题的关键.
八、解答题(本题满分14分)
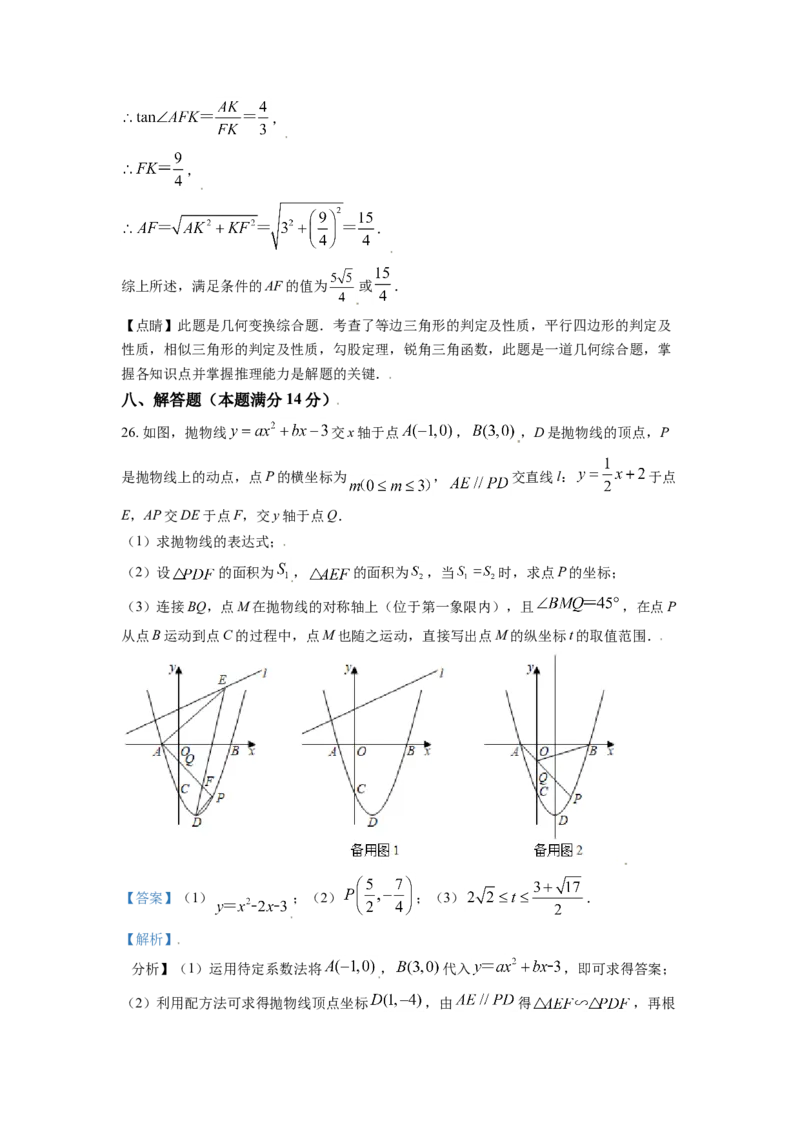
26. 如图,抛物线 交x轴于点 , ,D是抛物线的顶点,P
是抛物线上的动点,点P的横坐标为 , 交直线l: 于点
E,AP交DE于点F,交y轴于点Q.
(1)求抛物线的表达式;
(2)设 的面积为 , 的面积为 ,当 时,求点P的坐标;
(3)连接BQ,点M在抛物线的对称轴上(位于第一象限内),且 ,在点P
从点B运动到点C的过程中,点M也随之运动,直接写出点M的纵坐标t的取值范围.
【答案】(1) ;(2) ;(3) .
【解析】
【分析】(1)运用待定系数法将 , 代入 ,即可求得答案;
(2)利用配方法可求得抛物线顶点坐标 ,由 得 ,再根据 与 的面积相等,可得 ,故点F分别是AP、ED的中点,
设 , ,结合中点坐标公式建立方程求解即可;
(3)根据题意,分别求出t的最大值和最小值:①当点P与点B重合时,点Q与点O重合,
此时t的值最大,如图2,以OB为斜边在第一象限内作等腰直角 ,以 为圆心,
为半径作 ,交抛物线对称轴于点 ,过点 作 轴于点H,运用
勾股定理即可求得答案,②当点P与点C重合时,点Q与点C重合,此时t的值最小,如
图3,连接BC,以O为圆心,OB为半径作 交抛物线对称轴于点M,连接OM,设抛
物线对称轴交x轴于点E,运用勾股定理即可求得答案.
【详解】解:(1) 抛物线 交x轴于点 , ,
将A、B坐标分别代入抛物线解析式得: ,
解得: ,
抛物线的表达式为: ;
(2)如图,
D是抛物线的顶点,抛物线的表达式为: ,
,
交直线l: 于点E,P是抛物线上的动点,点P的横坐标为
,
,设 , ,
又 的面积为 , 的面积为 , ,
,
, ,即点F分别是AP、ED的中点,又 , , , ,
由中点坐标公式得: ,
解得: (与“ ”不符,应舍去), ,
,
, ;
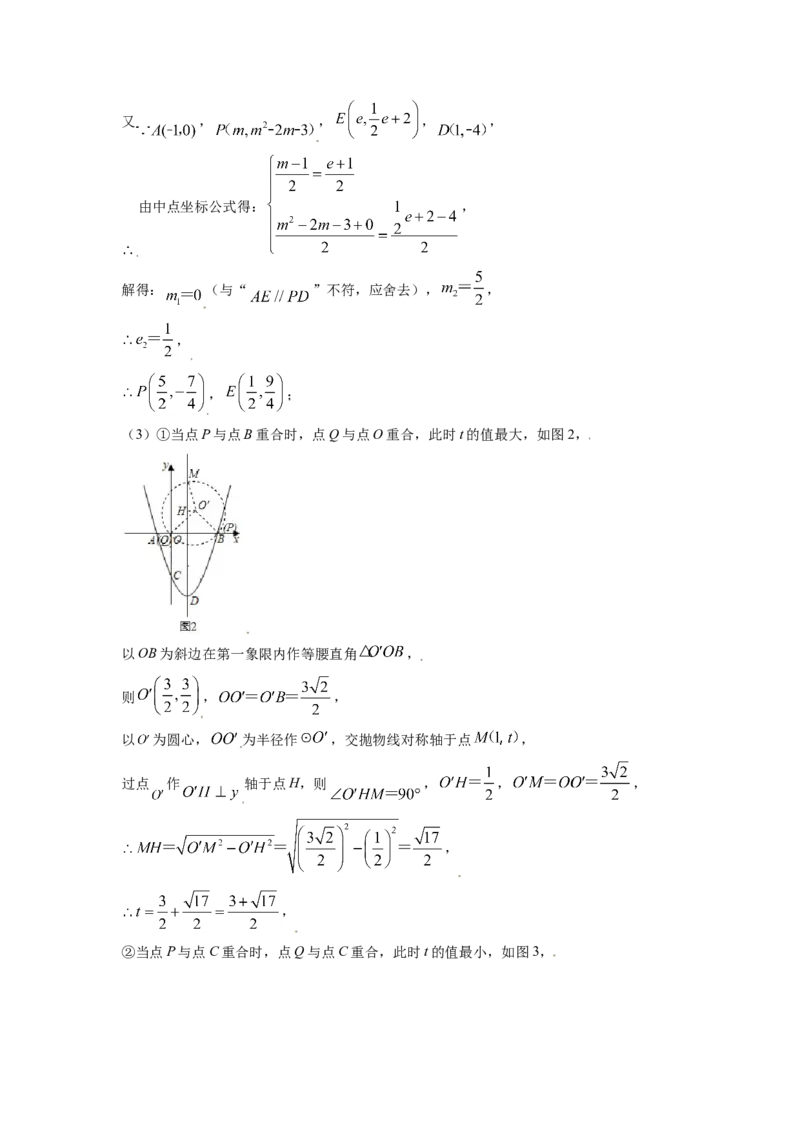
(3)①当点P与点B重合时,点Q与点O重合,此时t的值最大,如图2,
以OB为斜边在第一象限内作等腰直角 ,
则 , ,
以 为圆心, 为半径作 ,交抛物线对称轴于点 ,
过点 作 轴于点H,则 , , ,
,
,
②当点P与点C重合时,点Q与点C重合,此时t的值最小,如图3,连接BC,以O为圆心,OB为半径作 交抛物线对称轴于点M,
,
经过点C,
连接OM,设抛物线对称轴交x轴于点E,
则 , ,
,
,
,
综上所述, .
【点睛】此题属于二次函数综合题,考查代数计算问题,涉及勾股定理,三角形全等,二
元一次方程和一元二次方程的解及圆的相关知识,属于压轴题类型.