文档内容
2022 年辽宁省锦州市中考数学试卷
一、选择题(本大题共8小题,共16分.在每小题列出的选项中,选出符合题目的一项)
1. ﹣2022的绝对值是( )
A. B. C. 2022 D. ﹣2022
【答案】C
【解析】
【分析】根据绝对值的意义可直接得出答案.
【详解】解:−2022的绝对值是2022,
故选:C.
【点睛】本题考查了绝对值,掌握绝对值的意义是解题的关键.
2. 党的十八大以来,以习近平同志为核心的党中央重视技能人才的培育与发展.据报道,截至2021年底,
我国高技能人才超过60000000人,请将数据60000000用科学记数法表示为( )
A. B. C. D.
【答案】B
【解析】
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变
成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值大于或等于10时,n
是正整数;当原数的绝对值小于1时,n是负整数.
【详解】解:将数据60000000用科学记数法表示为 ;
故选B.
【点睛】本题主要考查科学记数法,熟练掌握科学记数法是解题的关键.
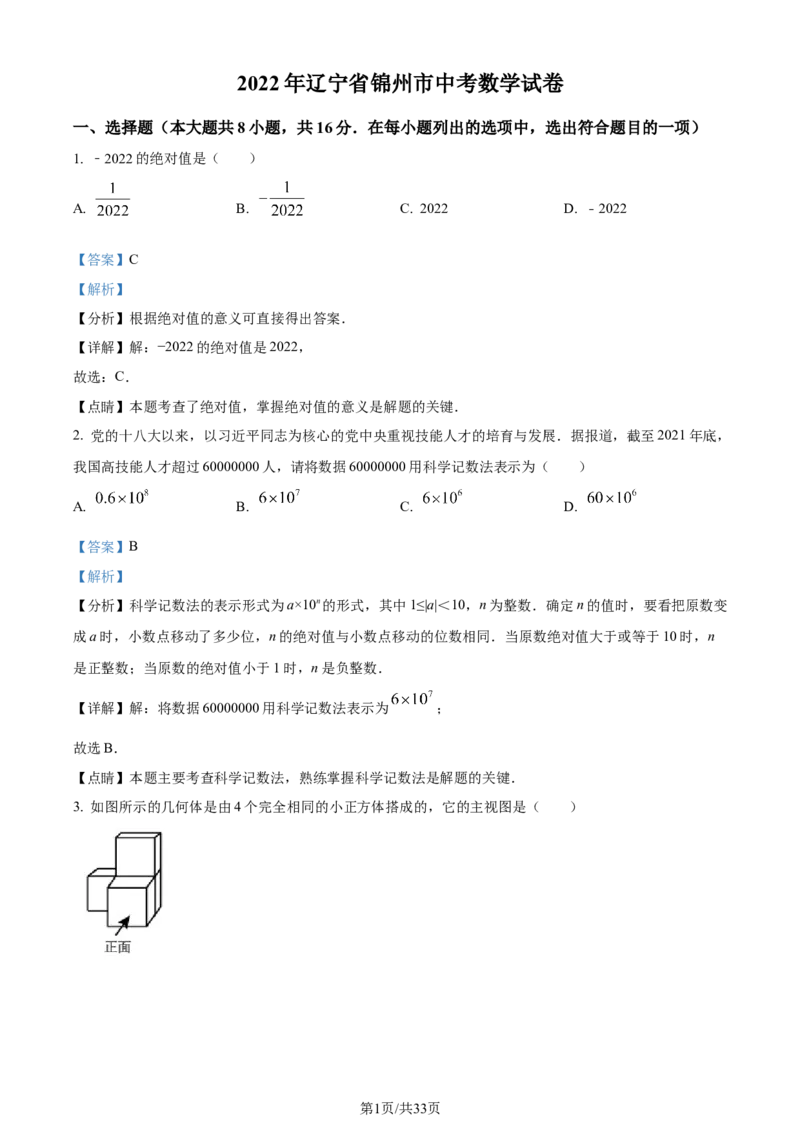
3. 如图所示的几何体是由4个完全相同的小正方体搭成的,它的主视图是( )
第1页/共33页
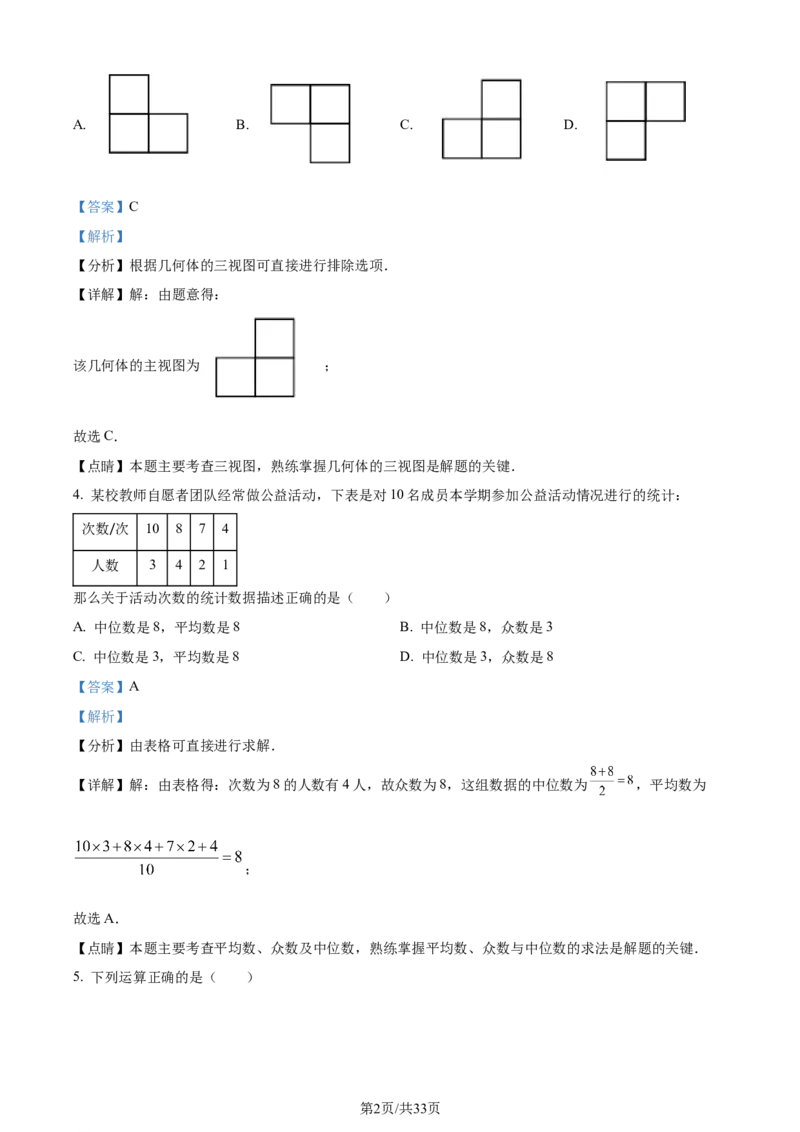
学科网(北京)股份有限公司A. B. C. D.
【答案】C
【解析】
【分析】根据几何体的三视图可直接进行排除选项.
【详解】解:由题意得:
该几何体的主视图为 ;
故选C.
【点睛】本题主要考查三视图,熟练掌握几何体的三视图是解题的关键.
4. 某校教师自愿者团队经常做公益活动,下表是对10名成员本学期参加公益活动情况进行的统计:
次数/次 10 8 7 4
人数 3 4 2 1
那么关于活动次数的统计数据描述正确的是( )
A. 中位数是8,平均数是8 B. 中位数是8,众数是3
C. 中位数是3,平均数是8 D. 中位数是3,众数是8
【答案】A
【解析】
【分析】由表格可直接进行求解.
【详解】解:由表格得:次数为8的人数有4人,故众数为8,这组数据的中位数为 ,平均数为
;
故选A.
【点睛】本题主要考查平均数、众数及中位数,熟练掌握平均数、众数与中位数的求法是解题的关键.
5. 下列运算正确的是( )
第2页/共33页
学科网(北京)股份有限公司A. B. C. D.
【答案】B
【解析】
【分析】分别根据幂的乘方运算法则,同底数幂的乘法法则,同底数幂的除法法则以及合并同类项逐一判
断即可.
【详解】解:A. ,故本选项不合题意;
B. ,故本选项符合题意;
C. ,故本选项不合题意;
D. ,故本选项不合题意.
故选:B.
【点睛】本题主要考查了同底数幂的乘除法以及幂的乘方与积的乘方,熟记这些运算法则是解答本题的关
键.
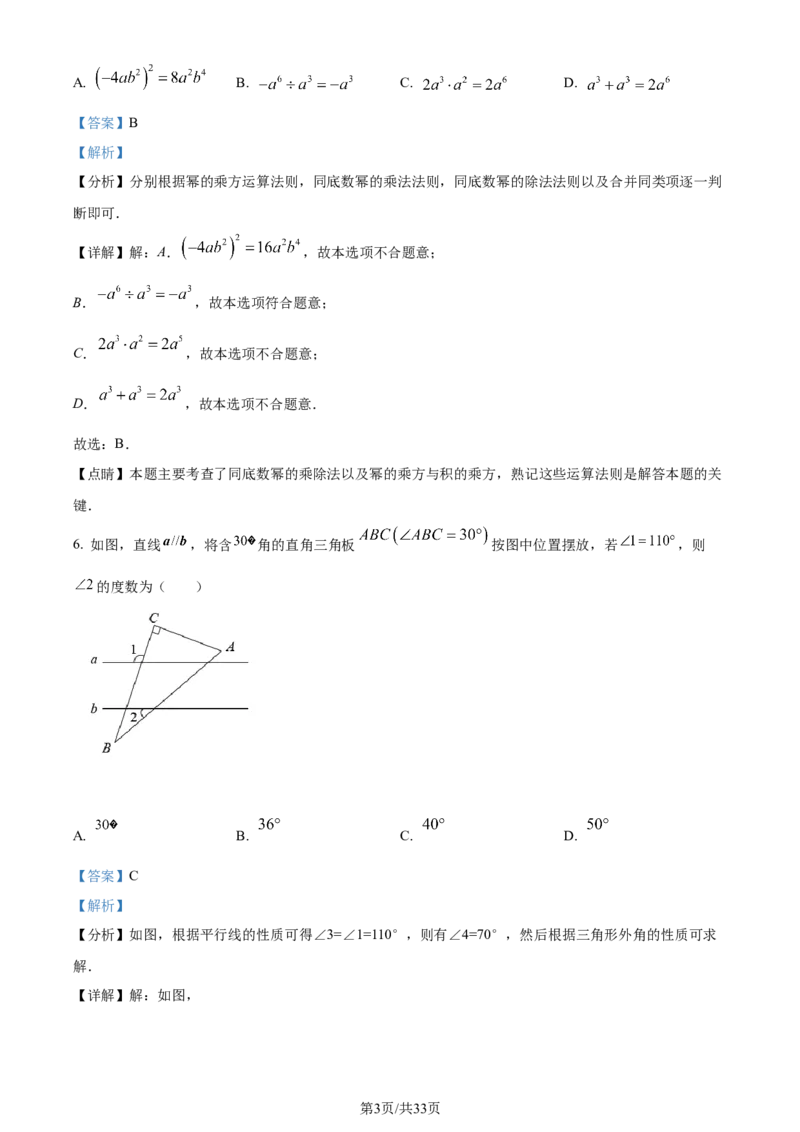
6. 如图,直线 ,将含 角的直角三角板 按图中位置摆放,若 ,则
的度数为( )
A. B. C. D.
【答案】C
【解析】
【分析】如图,根据平行线的性质可得∠3=∠1=110°,则有∠4=70°,然后根据三角形外角的性质可求
解.
【详解】解:如图,
第3页/共33页
学科网(北京)股份有限公司∵ , ,
∴∠3=∠1=110°,
∴ ,
∵
∴ ;
故选C.
【点睛】本题主要考查平行线的性质及三角形外角的性质,熟练掌握平行线的性质及三角形外角的性质是
解题的关键.
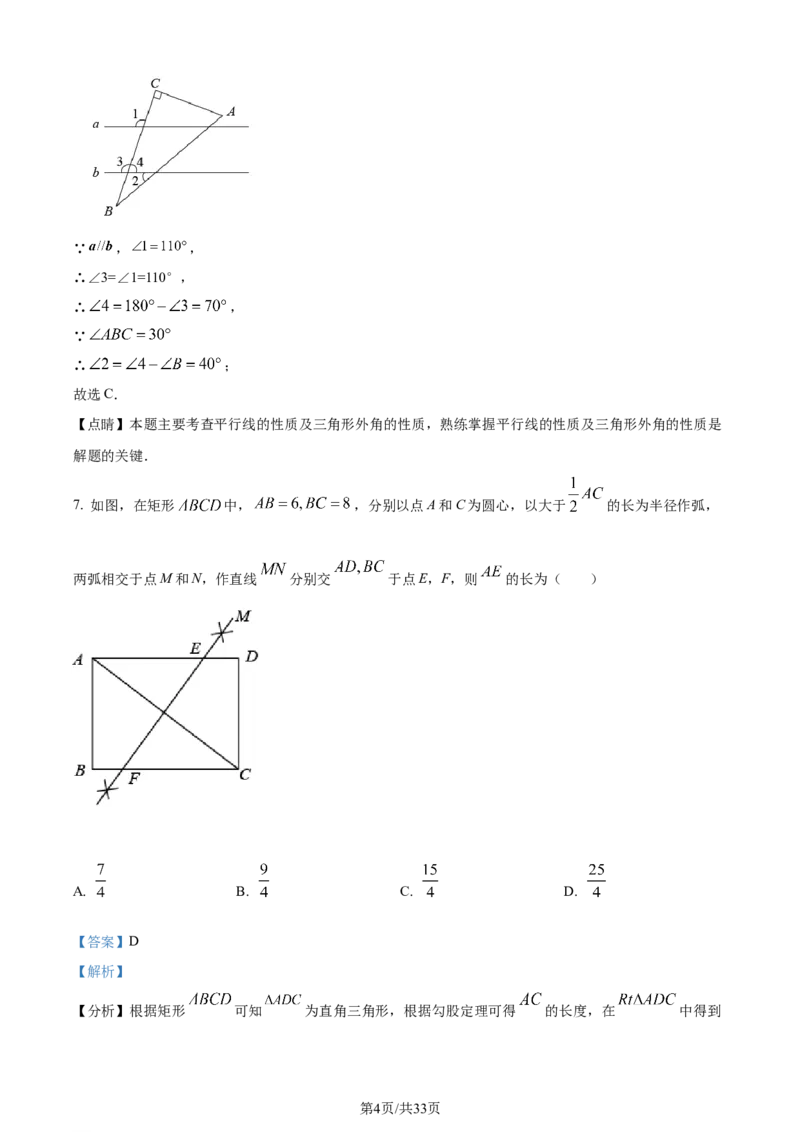
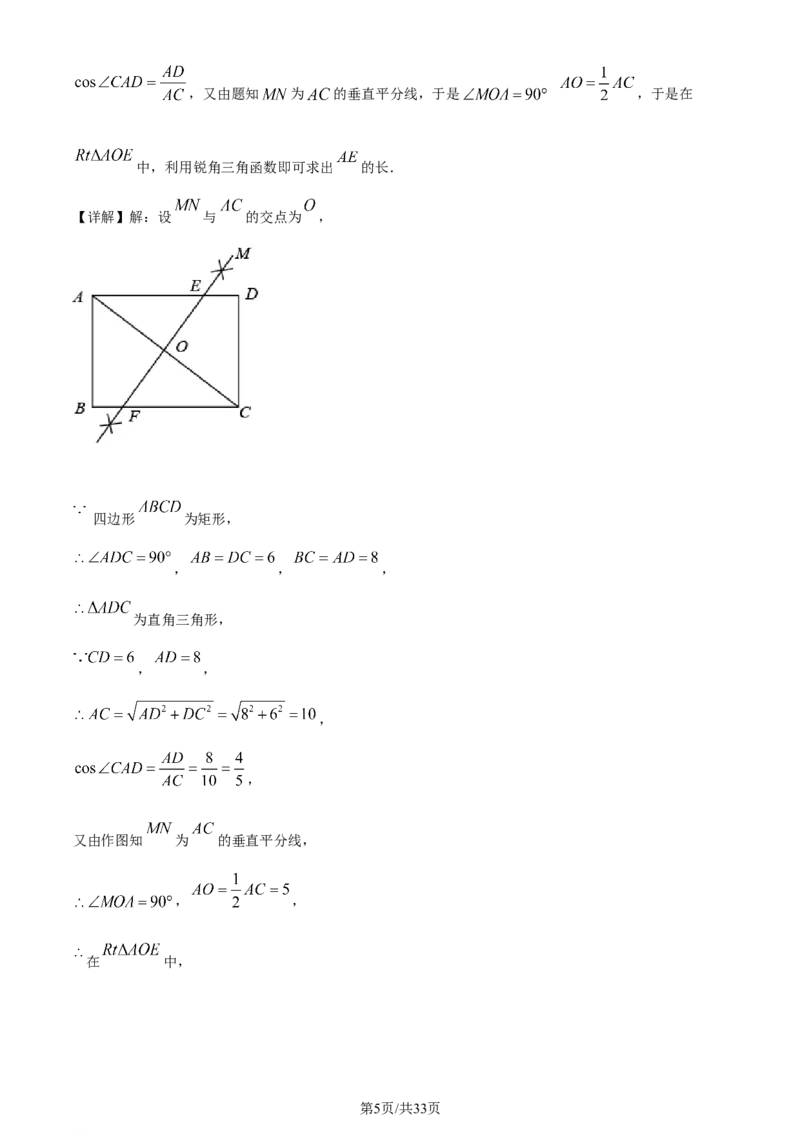
7. 如图,在矩形 中, ,分别以点A和C为圆心,以大于 的长为半径作弧,
两弧相交于点M和N,作直线 分别交 于点E,F,则 的长为( )
A. B. C. D.
【答案】D
【解析】
【分析】根据矩形 可知 为直角三角形,根据勾股定理可得 的长度,在 中得到
第4页/共33页
学科网(北京)股份有限公司,又由题知 为 的垂直平分线,于是 ,于是在
中,利用锐角三角函数即可求出 的长.
【详解】解:设 与 的交点为 ,
四边形 为矩形,
, , ,
为直角三角形,
, ,
,
,
又由作图知 为 的垂直平分线,
, ,
在 中,
第5页/共33页
学科网(北京)股份有限公司,
,
,
.
故选:D.
【点睛】本题主要考查矩形的性质,锐角三角函数,垂直平分线,勾股定理,掌握定理以及性质是解题的
关键.
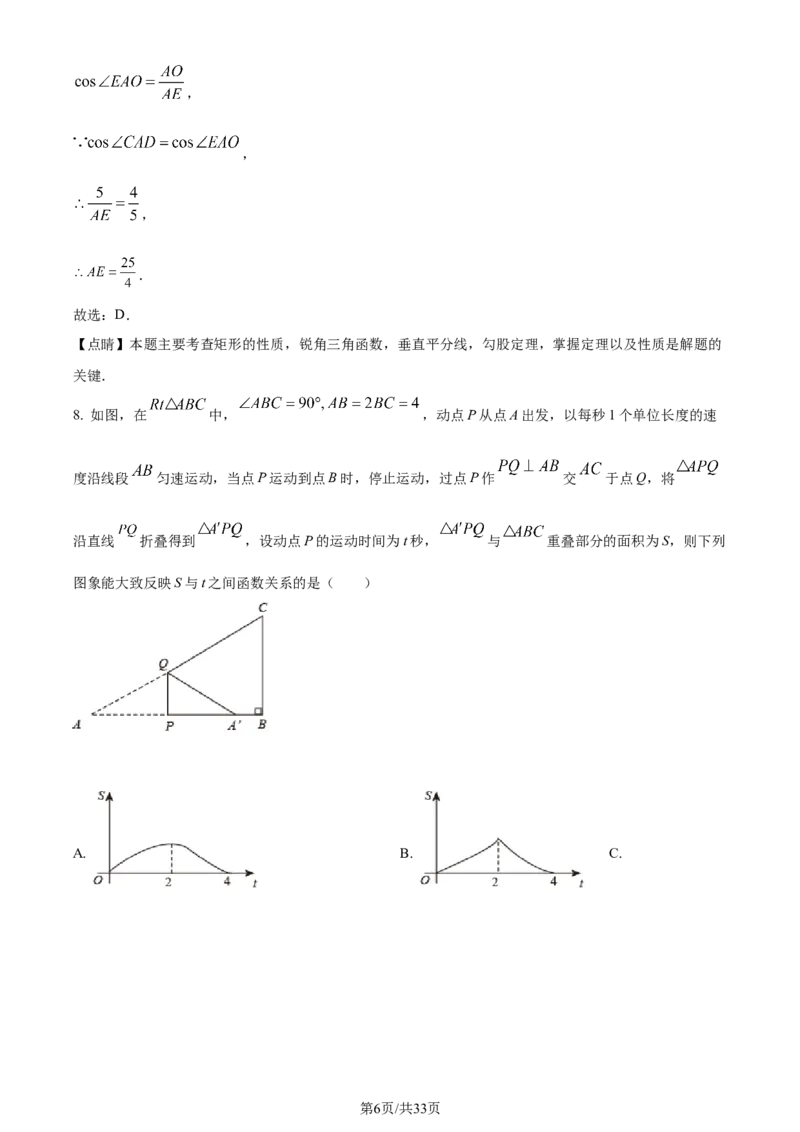
8. 如图,在 中, ,动点P从点A出发,以每秒1个单位长度的速
度沿线段 匀速运动,当点P运动到点B时,停止运动,过点P作 交 于点Q,将
沿直线 折叠得到 ,设动点P的运动时间为t秒, 与 重叠部分的面积为S,则下列
图象能大致反映S与t之间函数关系的是( )
A. B. C.
第6页/共33页
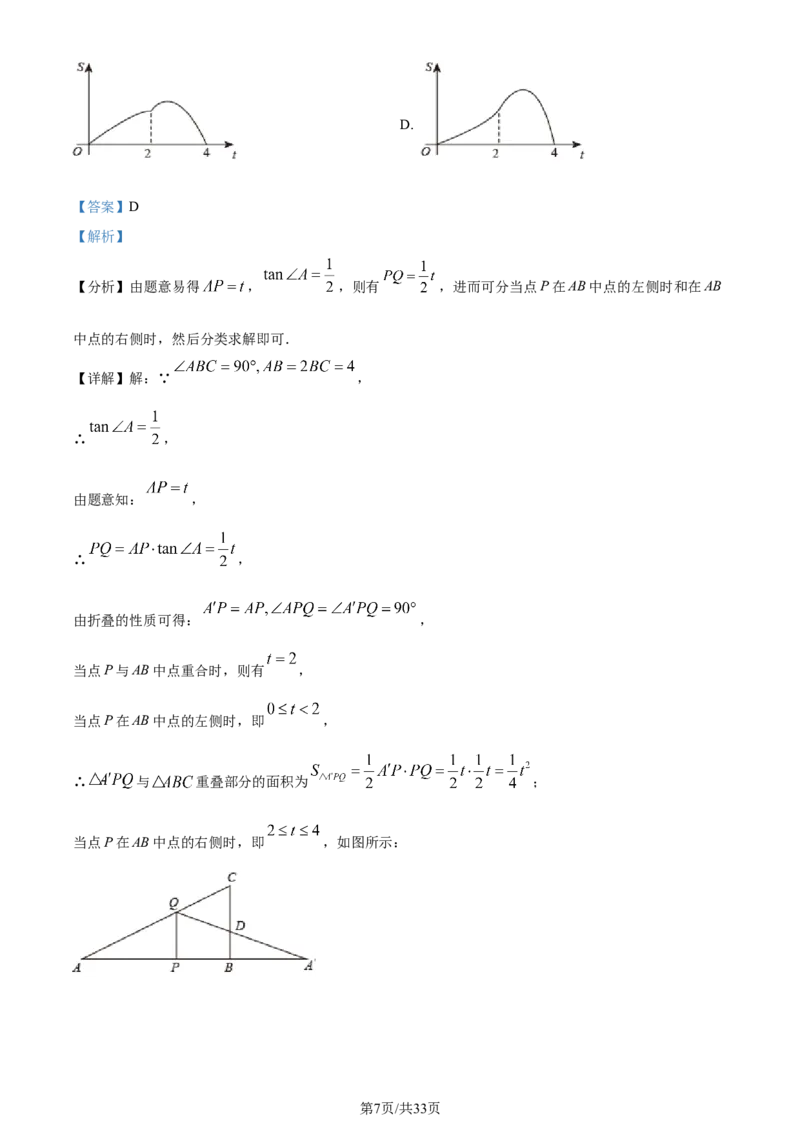
学科网(北京)股份有限公司D.
【答案】D
【解析】
【分析】由题意易得 , ,则有 ,进而可分当点P在AB中点的左侧时和在AB
中点的右侧时,然后分类求解即可.
【详解】解:∵ ,
∴ ,
由题意知: ,
∴ ,
由折叠的性质可得: ,
当点P与AB中点重合时,则有 ,
当点P在AB中点的左侧时,即 ,
∴ 与 重叠部分的面积为 ;
当点P在AB中点的右侧时,即 ,如图所示:
第7页/共33页
学科网(北京)股份有限公司由折叠性质可得: , ,
∴ ,
∴ ,
∴ ,
∴ 与 重叠部分的面积为
;
综上所述:能反映 与 重叠部分的面积S与t之间函数关系的图象只有D选项;
故选D.
【点睛】本题主要考查二次函数的图象及三角函数,熟练掌握二次函数的图象及三角函数是解题的关键.
二、填空题(本大题共8小题,共24分)
9. 甲、乙两名学生10次立定跳远成绩的平均数相同,若甲生10次立定跳远成绩的方差为 ,乙生
10次立定跳远成绩的方差为 ,则甲、乙两名学生10次立定跳远成绩比较稳定的是___________.
(填“甲”或“乙”)
【答案】乙
【解析】
【分析】根据方差可直接进行求解.
【详解】解:由 , 可知: ,且甲、乙两名学生10次立定跳远成绩的平均数相
同,所以甲、乙两名学生10次立定跳远成绩比较稳定的是乙;
故答案为乙.
【点睛】本题主要考查方差,熟练掌握方差的相关知识点是解题的关键.
10. 在一个不透明的口袋中装有红球和白球共8个,这些球除颜色外都相同,将口袋中的球搅匀后,从中
随机摸出一个球,记下它的颜色后再放回口袋中,不断重复这一过程,共摸了100次球,发现有75次摸到
红球,则口袋中红球的个数约为___________.
【答案】6
第8页/共33页
学科网(北京)股份有限公司【解析】
【分析】用球的总个数乘以摸到红球的频率即可.
【详解】解:估计这个口袋中红球的数量为8× =6(个).
故答案为:6.
【点睛】本题考查了利用频率估计概率:大量重复实验时,事件发生的频率在某个固定位置左右摆动,并
且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似
值就是这个事件的概率,用频率估计概率得到的是近似值,随实验次数的增多,值越来越精确.
11. 若关于x的一元二次方程x2+3x+k=0有两个不相等的实数根,则k的取值范围是_____.
【答案】k<
【解析】
【
详解】解:由题意得: =9﹣4k>0,
△
解得:k< ,
故答案为:k< .
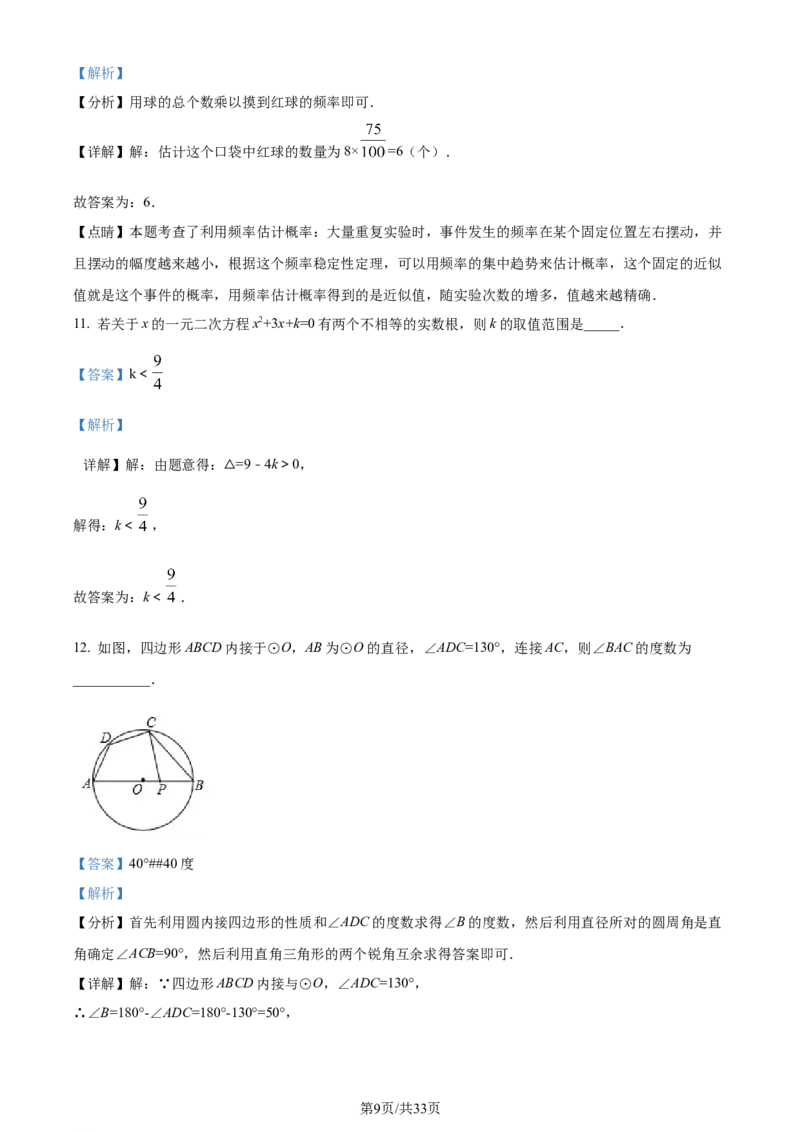
12. 如图,四边形ABCD内接于⊙O,AB为⊙O的直径,∠ADC=130°,连接AC,则∠BAC的度数为
___________.
【答案】40°##40度
【解析】
【分析】首先利用圆内接四边形的性质和∠ADC的度数求得∠B的度数,然后利用直径所对的圆周角是直
角确定∠ACB=90°,然后利用直角三角形的两个锐角互余求得答案即可.
【详解】解:∵四边形ABCD内接与⊙O,∠ADC=130°,
∴∠B=180°-∠ADC=180°-130°=50°,
第9页/共33页
学科网(北京)股份有限公司∵AB为直径,
∴∠ACB=90°,
∴∠CAB=90°-∠B=90°-50°=40°,
故答案为:40°.
【点睛】本题考查了圆内接四边形的性质及圆周角定理的知识,解题的关键是了解圆内接四边形的对角互
补.
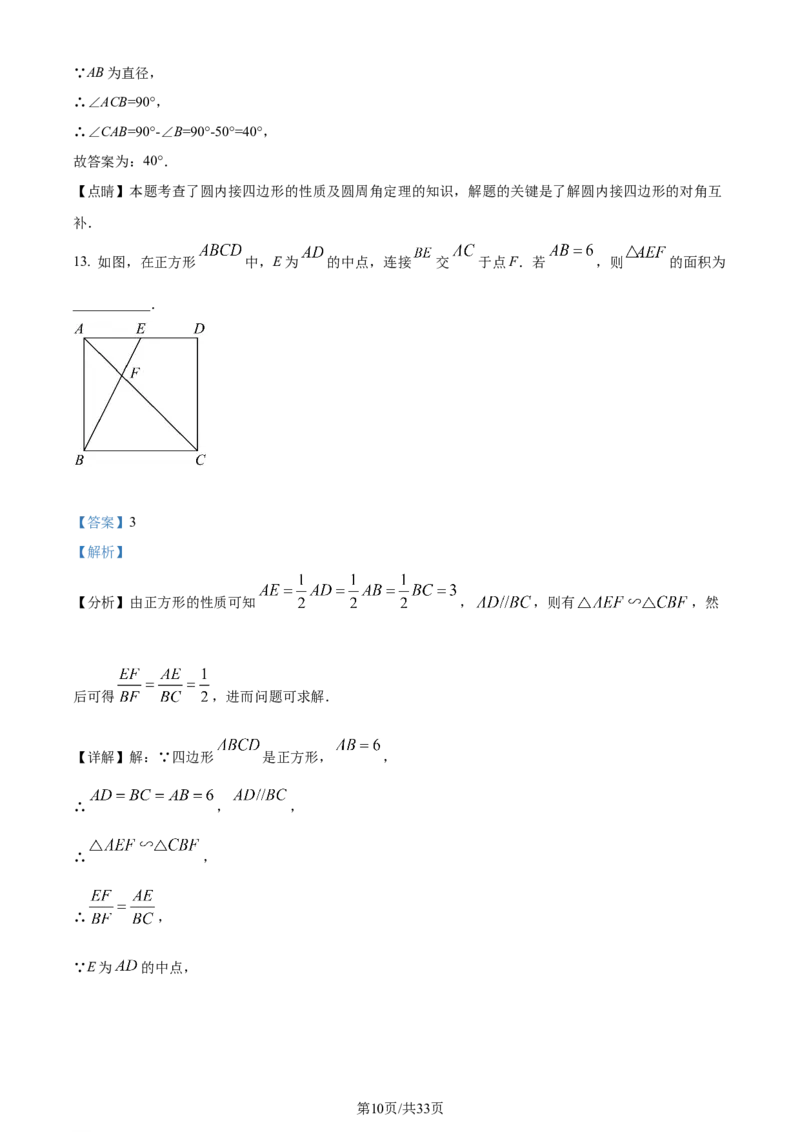
13. 如图,在正方形 中,E为 的中点,连接 交 于点F.若 ,则 的面积为
___________.
【答案】3
【解析】
【分析】由正方形的性质可知 , ,则有 ,然
后可得 ,进而问题可求解.
【详解】解:∵四边形 是正方形, ,
∴ , ,
∴ ,
∴ ,
∵E为 的中点,
第10页/共33页
学科网(北京)股份有限公司∴ ,
∴ , ,
∴ ,
∴ ;
故答案为3.
【点睛】本题主要考查正方形的性质及相似三角形的性质与判定,熟练掌握正方形的性质及相似三角形的
性质与判定是解题的关键.
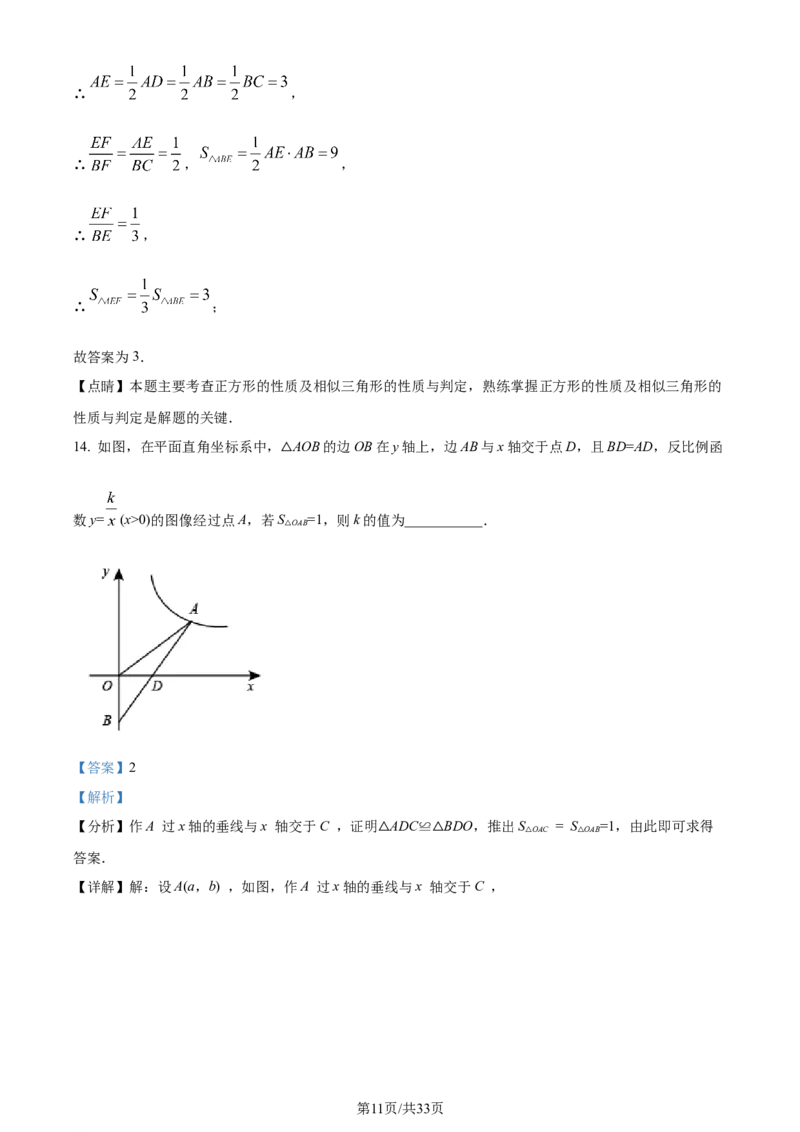
14. 如图,在平面直角坐标系中, AOB的边OB在y轴上,边AB与x轴交于点D,且BD=AD,反比例函
△
数y= (x>0)的图像经过点A,若S =1,则k的值为___________.
OAB
△
【答案】2
【解析】
【分析】作A 过x轴的垂线与x 轴交于C ,证明 ADC≌ BDO,推出S = S =1,由此即可求得
OAC OAB
△ △
答案. △ △
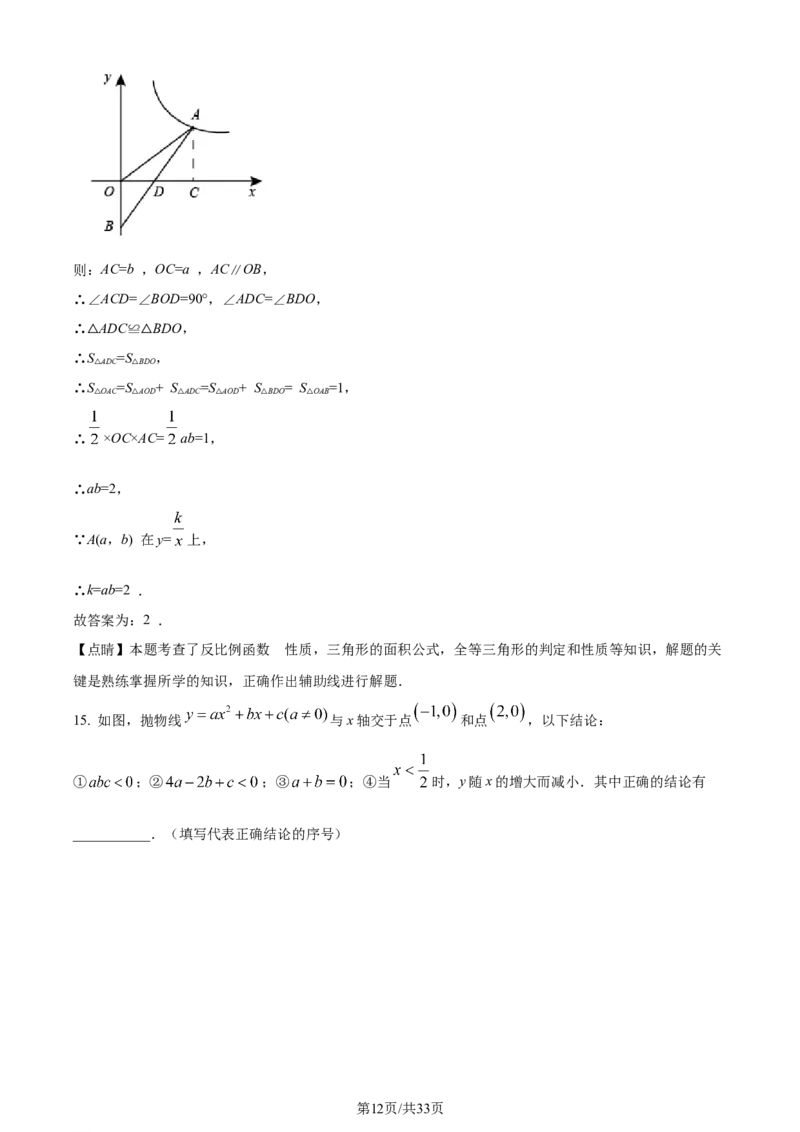
【详解】解:设A(a,b) ,如图,作A 过x轴的垂线与x 轴交于C ,
第11页/共33页
学科网(北京)股份有限公司则:AC=b ,OC=a ,AC∥OB,
∴∠ACD=∠BOD=90°,∠ADC=∠BDO,
∴ ADC≌ BDO,
∴△S ADC =S B△DO ,
△ △
∴S =S + S =S + S = S =1,
OAC AOD ADC AOD BDO OAB
△ △ △ △ △ △
∴ ×OC×AC= ab=1,
∴ab=2,
∵A(a,b) 在y= 上,
∴k=ab=2 .
故答案为:2 .
【点睛】本题考查了反比例函数 的性质,三角形的面积公式,全等三角形的判定和性质等知识,解题的关
键是熟练掌握所学的知识,正确作出辅助线进行解题.
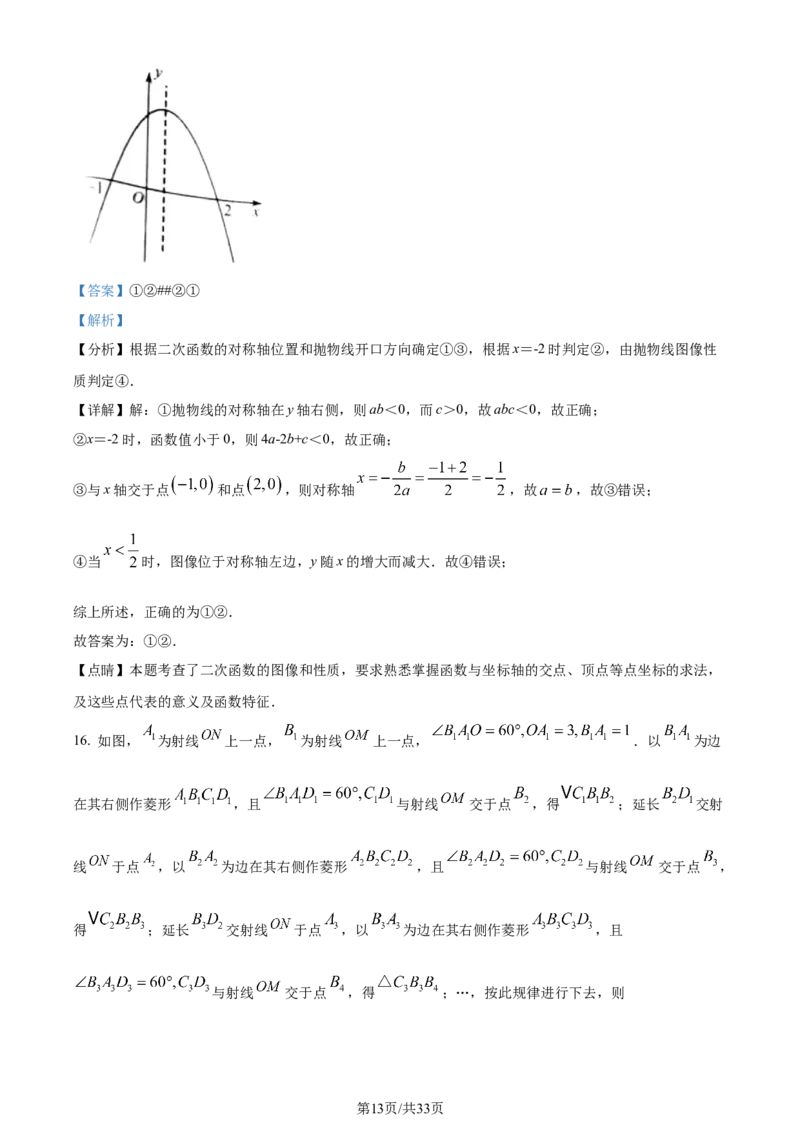
15. 如图,抛物线 与x轴交于点 和点 ,以下结论:
① ;② ;③ ;④当 时,y随x的增大而减小.其中正确的结论有
___________.(填写代表正确结论的序号)
第12页/共33页
学科网(北京)股份有限公司【答案】①②##②①
【解析】
【分析】根据二次函数的对称轴位置和抛物线开口方向确定①③,根据x=-2时判定②,由抛物线图像性
质判定④.
【详解】解:①抛物线的对称轴在y轴右侧,则ab<0,而c>0,故abc<0,故正确;
②x=-2时,函数值小于0,则4a-2b+c<0,故正确;
③与x轴交于点 和点 ,则对称轴 ,故 ,故③错误;
④当 时,图像位于对称轴左边,y随x的增大而减大.故④错误;
综上所述,正确的为①②.
故答案为:①②.
【点睛】本题考查了二次函数的图像和性质,要求熟悉掌握函数与坐标轴的交点、顶点等点坐标的求法,
及这些点代表的意义及函数特征.
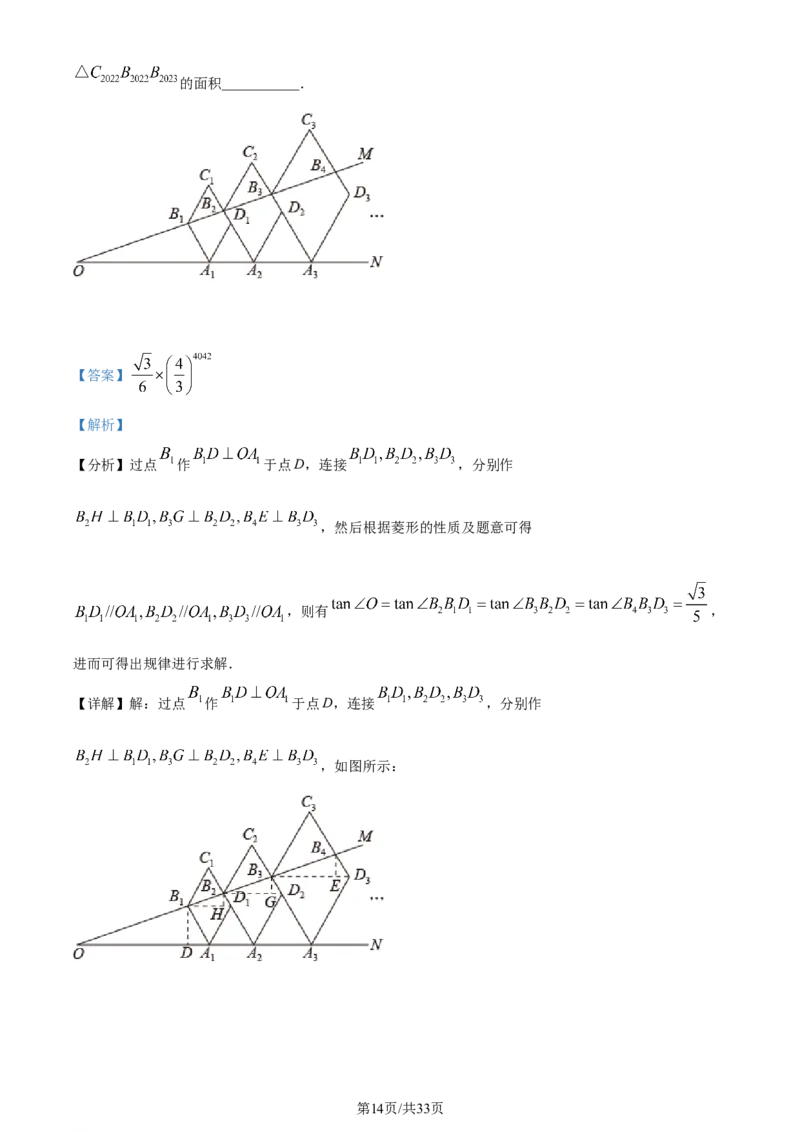
16. 如图, 为射线 上一点, 为射线 上一点, .以 为边
在其右侧作菱形 ,且 与射线 交于点 ,得 ;延长 交射
线 于点 ,以 为边在其右侧作菱形 ,且 与射线 交于点 ,
得 ;延长 交射线 于点 ,以 为边在其右侧作菱形 ,且
与射线 交于点 ,得 ;…,按此规律进行下去,则
第13页/共33页
学科网(北京)股份有限公司的面积___________.
【答案】
【解析】
【分析】过点 作 于点D,连接 ,分别作
,然后根据菱形的性质及题意可得
,则有 ,
进而可得出规律进行求解.
【详解】解:过点 作 于点D,连接 ,分别作
,如图所示:
第14页/共33页
学科网(北京)股份有限公司∴ ,
∵ ,
∴ ,
∵ , ,
∴ , ,
∴ ,
∴ ,
∵菱形 ,且 ,
∴ 是等边三角形,
∴ , ,
∵ ,
∴ ,
∴ ,
∴ ,
设 ,
∵ ,
∴ ,
第15页/共33页
学科网(北京)股份有限公司∴ ,
∴ ,解得: ,
∴ ,
∴ ,
同理可得: , ,
∴ ,
由上可得: , ,
∴
,
故答案 .
为
【点睛】本题主要考查菱形的性质、等边三角形的性质与判定、含30度直角三角形的性质及三角函数,熟
练掌握菱形的性质、等边三角形的性质与判定、含30度直角三角形的性质及三角函数是解题的关键.
三、解答题(本大题共9小题,共80分.解答应写出文字说明,证明过程或演算步骤)
17. 先化简,再求值: ,其中 .
【答案】 ,
【解析】
第16页/共33页
学科网(北京)股份有限公司【分析】先对分式进行化简,然后再代入求解即可.
【详解】解:原式=
=
=
= ,
把 代入得:原式= .
【点睛】本题主要考查分式的化简求值及二次根式的运算,熟练掌握分式的化简求值及二次根式的运算是
解题的关键.
18. 某校为了传承中华优秀传统文化,举行“薪火传承育新人”系列活动,组建了四个活动小组:A(经典诵
读),B(诗词大赛),C(传统故事),D(汉字听写).学校规定:每名学生必须参加且只能参加其中
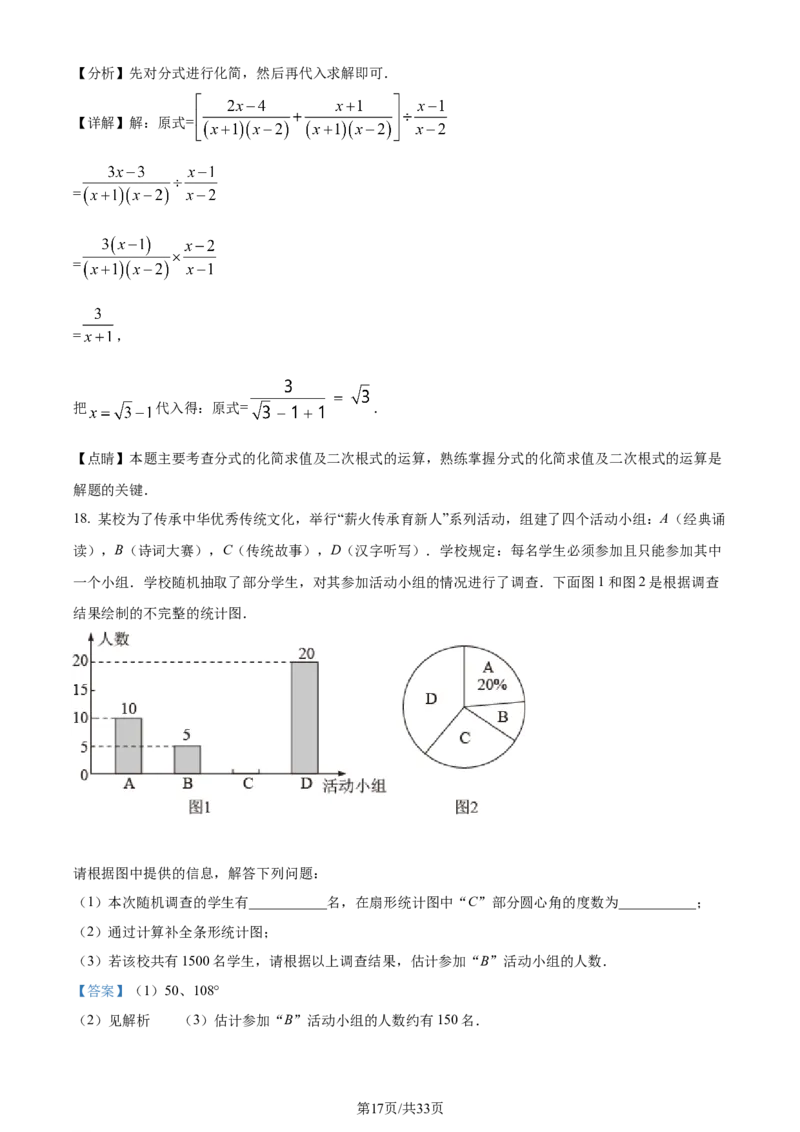
一个小组.学校随机抽取了部分学生,对其参加活动小组的情况进行了调查.下面图1和图2是根据调查
结果绘制的不完整的统计图.
请根据图中提供的信息,解答下列问题:
(1)本次随机调查的学生有___________名,在扇形统计图中“C”部分圆心角的度数为___________;
(2)通过计算补全条形统计图;
(3)若该校共有1500名学生,请根据以上调查结果,估计参加“B”活动小组的人数.
【答案】(1)50、108°
(2)见解析 (3)估计参加“B”活动小组的人数约有150名.
第17页/共33页
学科网(北京)股份有限公司【解析】
【分析】(1)由A的人数及其所占百分比可得总人数,根据各类型人数之和等于总人数求得C的人数,
用360°乘以C人数所占比例即可得其对应圆心角度数;
(2)据(1)的数据补全图形即可得;
(3)总人数乘以B活动小组人数和所占比例即可;
【小问1详解】
解:本次调查的总人数为10÷20%=50(名),
C活动小组人数为50-(10+5+20)=15(名),
扇形统计图中,C所对应的扇形的圆心角度数是360°× =108°,
故答案为:50、108°;
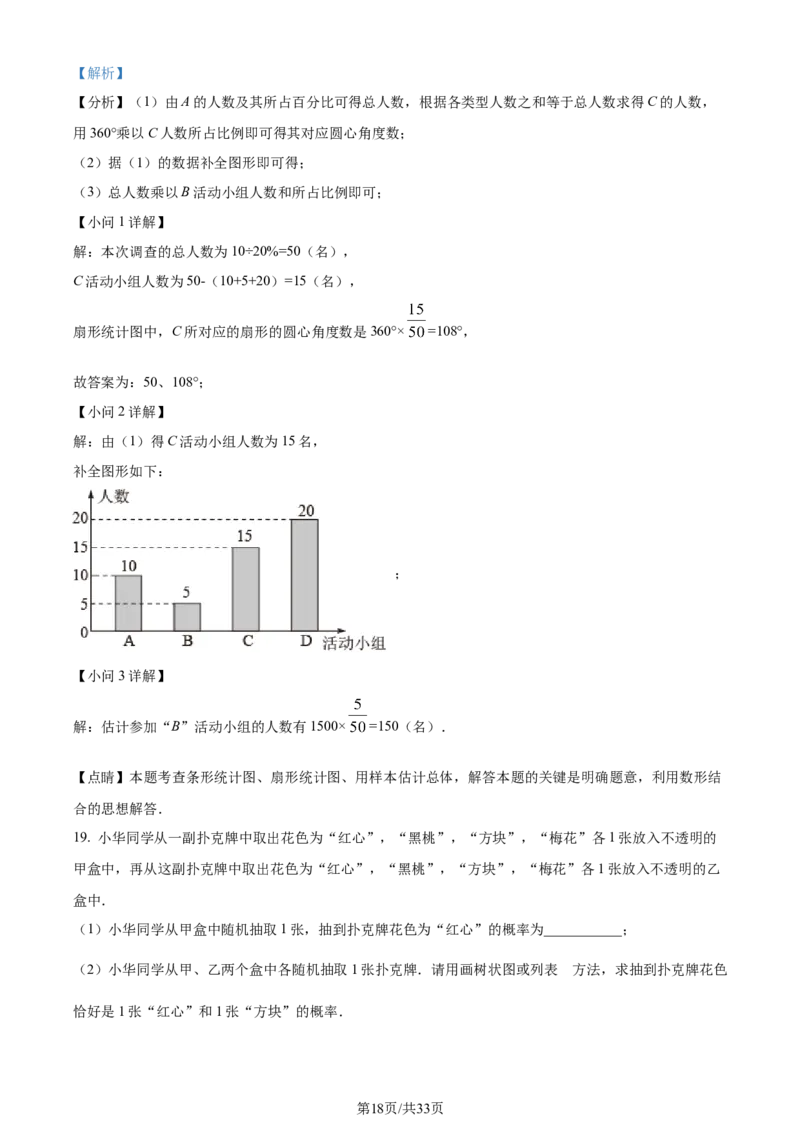
【小问2详解】
解:由(1)得C活动小组人数为15名,
补全图形如下:
;
【小问3详解】
解:估计参加“B”活动小组的人数有1500× =150(名).
【点睛】本题考查条形统计图、扇形统计图、用样本估计总体,解答本题的关键是明确题意,利用数形结
合的思想解答.
19. 小华同学从一副扑克牌中取出花色为“红心”,“黑桃”,“方块”,“梅花”各1张放入不透明的
甲盒中,再从这副扑克牌中取出花色为“红心”,“黑桃”,“方块”,“梅花”各1张放入不透明的乙
盒中.
(1)小华同学从甲盒中随机抽取1张,抽到扑克牌花色为“红心”的概率为___________;
的
(2)小华同学从甲、乙两个盒中各随机抽取1张扑克牌.请用画树状图或列表 方法,求抽到扑克牌花色
恰好是1张“红心”和1张“方块”的概率.
第18页/共33页
学科网(北京)股份有限公司【答案】(1)
(2)
【解析】
【分析】(1)先求出从甲盒中随机抽取1张有4种等可能的结果,抽到扑克牌花色为“红心”结果只有1
种,再利用概率公式求解;
(2)先列出表,进而得到从甲、乙两个盒中各随机抽取1张扑克牌共有16种等可能的结果,其中抽到扑
克牌花色恰好是1张“红心”和1张“方块”的结果有2种,利用概率公式求解.
【小问1详解】
解:根据题意可知
从甲盒中随机抽取1张有4种等可能的结果,抽到扑克牌花色为“红心”结果只有1种,
所以抽到扑克牌花色为“红心”的概率为 .
故答案为: ;
【小问2详解】
解:列表如下:
红心 黑桃 方块 梅花
甲 甲 甲 甲
红心 红心 ,红心 黑桃 ,红心 方块 ,红心 梅花 ,红心
乙 甲 乙 甲 乙 甲 乙 甲 乙
黑桃 红心 ,黑桃 黑桃 ,黑桃 方块 ,黑桃 梅花 ,黑桃
乙 甲 乙 甲 乙 甲 乙 甲 乙
方块 红心 ,方块 黑桃 ,方块 方块 ,方块 梅花 ,方块
乙 甲 乙 甲 乙 甲 乙 甲 乙
梅花 红心 ,梅花 黑桃 ,梅花 方块 ,梅花 梅花 ,梅花
乙 甲 乙 甲 乙 甲 乙 甲 乙
从图中可知,从甲、乙两个盒中各随机抽取1张扑克牌共有16种等可能的结果,其中抽到扑克牌花色恰好
是1张“红心”和1张“方块”的结果有2种,
所以抽到扑克牌花色恰好是1张“红心”和1张“方块”的概率是 .
【点睛】本题主要考查了概率公式和用树状图或列表法求概率,理解相关知识是解答关键.
20. 2022年3月23日“天官课堂”第二课在中国空间站开讲了,精彩的直播激发了学生探索科学奥秘的兴
第19页/共33页
学科网(北京)股份有限公司趣.某中学为满足学生的需求,充实物理兴趣小组的实验项目,决定购入A、B两款物理实验套装,其中
A款套装单价是B款套装单价的1.2倍,用9900元购买的A款套装数量比用7500元购买的B款套装数量多
5套.求A、B两款套装的单价分别是多少元.
【答案】A款套装的单价是180元、B款套装的单价是150元.
【解析】
【分析】设B款套装的单价是x元,则A款套装的单价是1.2x元,即可得出关于x的分式方程,解之经检
验后即可得出结论.
【详解】解:设B款套装的单价是x元,则A款套装的单价是1.2x元,
由题意得: ,
解得:x=150,
经检验,x=150是原方程的解,且符合题意,
∴1.2x=180.
答:A款套装的单价是180元、B款套装的单价是150元.
【点睛】本题考查了分式方程的应用,解题的关键是:找准等量关系,正确列出分式方程.
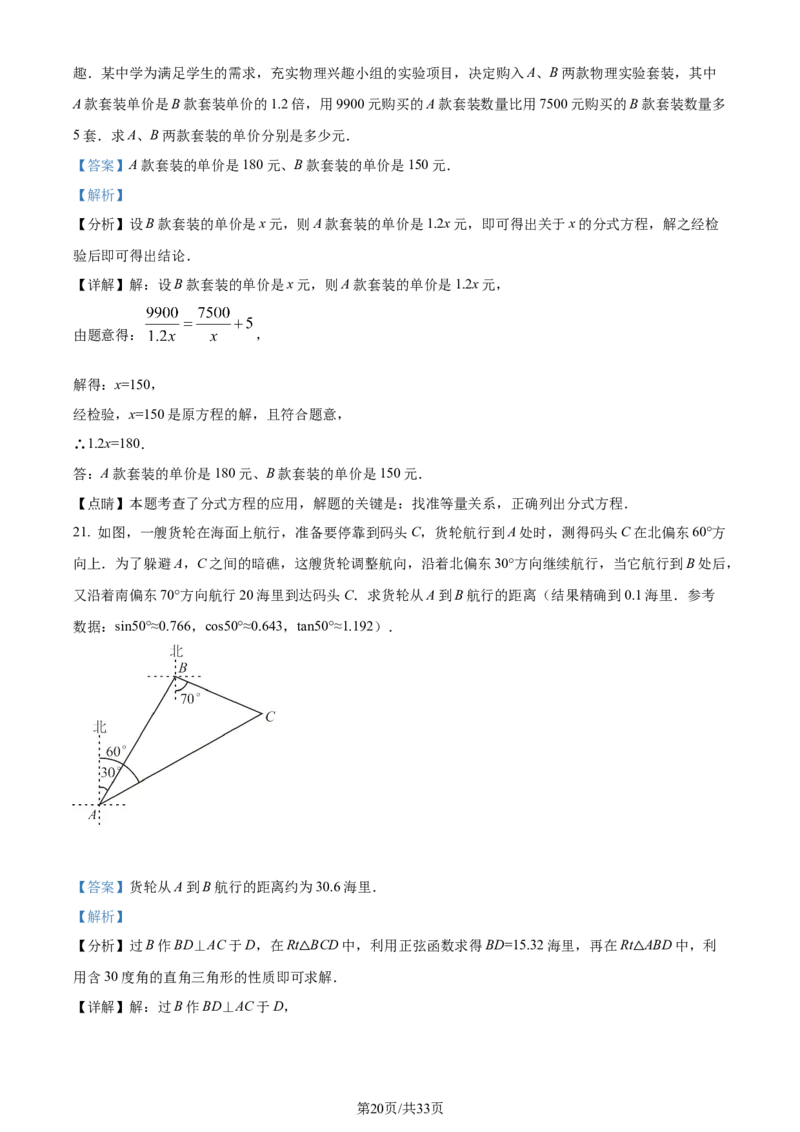
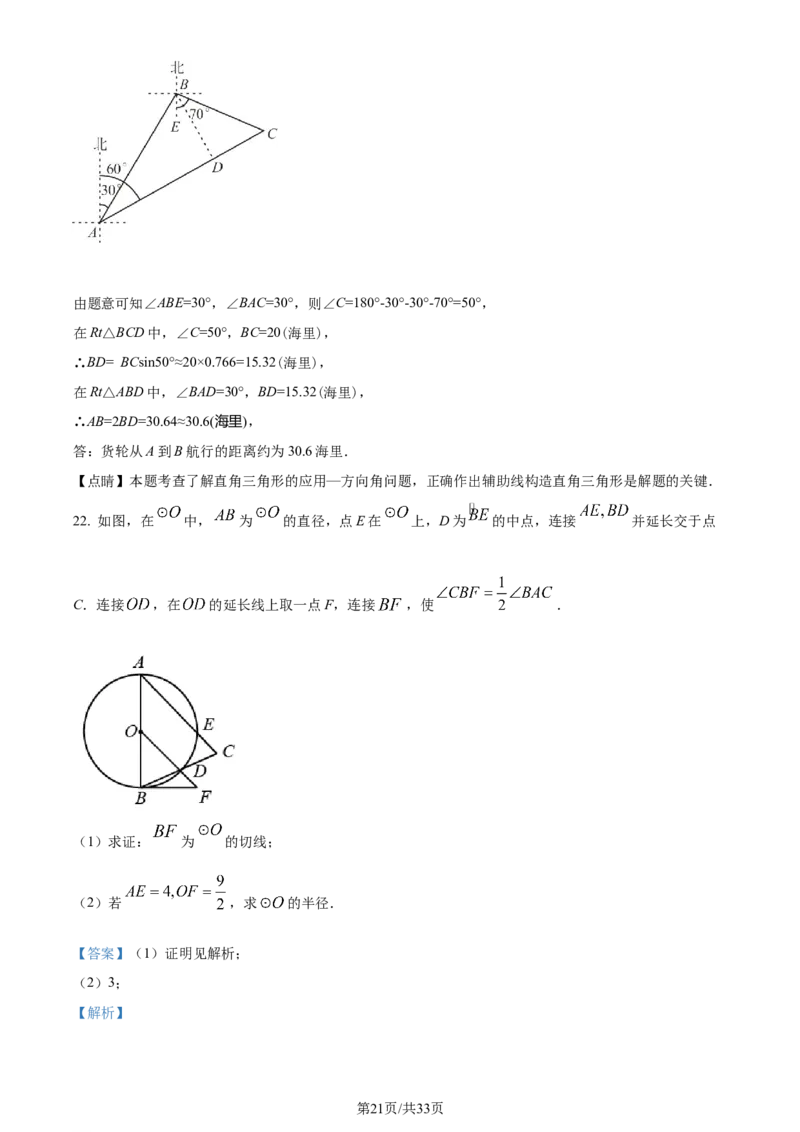
21. 如图,一艘货轮在海面上航行,准备要停靠到码头C,货轮航行到A处时,测得码头C在北偏东60°方
向上.为了躲避A,C之间的暗礁,这艘货轮调整航向,沿着北偏东30°方向继续航行,当它航行到B处后,
又沿着南偏东70°方向航行20海里到达码头C.求货轮从A到B航行的距离(结果精确到0.1海里.参考
数据:sin50°≈0.766,cos50°≈0.643,tan50°≈1.192).
【答案】货轮从A到B航行的距离约为30.6海里.
【解析】
【分析】过B作BD⊥AC于D,在Rt BCD中,利用正弦函数求得BD=15.32海里,再在Rt ABD中,利
用含30度角的直角三角形的性质即可△求解. △
【详解】解:过B作BD⊥AC于D,
第20页/共33页
学科网(北京)股份有限公司由题意可知∠ABE=30°,∠BAC=30°,则∠C=180°-30°-30°-70°=50°,
在Rt△BCD中,∠C=50°,BC=20(海里),
∴BD= BCsin50°≈20×0.766=15.32(海里),
在Rt△ABD中,∠BAD=30°,BD=15.32(海里),
∴AB=2BD=30.64≈30.6(海里),
答:货轮从A到B航行的距离约为30.6海里.
【点睛】本题考查了解直角三角形的应用—方向角问题,正确作出辅助线构造直角三角形是解题的关键.
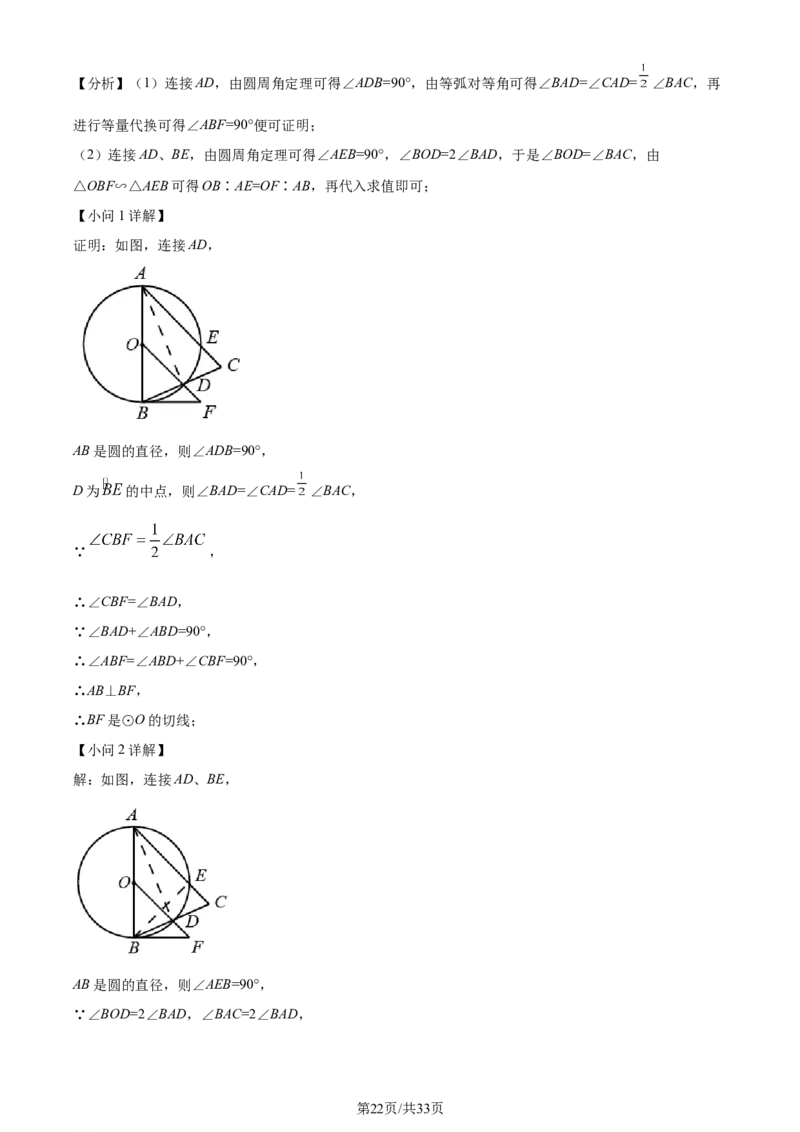
22. 如图,在 中, 为 的直径,点E在 上,D为 的中点,连接 并延长交于点
C.连接 ,在 的延长线上取一点F,连接 ,使 .
(1)求证: 为 的切线;
(2)若 ,求 的半径.
【答案】(1)证明见解析;
(2)3;
【解析】
第21页/共33页
学科网(北京)股份有限公司【分析】(1)连接AD,由圆周角定理可得∠ADB=90°,由等弧对等角可得∠BAD=∠CAD= ∠BAC,再
进行等量代换可得∠ABF=90°便可证明;
(2)连接AD、BE,由圆周角定理可得∠AEB=90°,∠BOD=2∠BAD,于是∠BOD=∠BAC,由
△OBF∽△AEB可得OB∶AE=OF∶AB,再代入求值即可;
【小问1详解】
证明:如图,连接AD,
AB是圆的直径,则∠ADB=90°,
D为 的中点,则∠BAD=∠CAD= ∠BAC,
∵ ,
∴∠CBF=∠BAD,
∵∠BAD+∠ABD=90°,
∴∠ABF=∠ABD+∠CBF=90°,
∴AB⊥BF,
∴BF是⊙O的切线;
【小问2详解】
解:如图,连接AD、BE,
AB是圆的直径,则∠AEB=90°,
∵∠BOD=2∠BAD,∠BAC=2∠BAD,
第22页/共33页
学科网(北京)股份有限公司∴∠BOD=∠BAC,
又∵∠ABF=∠AEB=90°,
∴△OBF∽△AEB,
∴OB∶AE=OF∶AB,
∴OB∶4= ∶2OB,OB2=9,
OB>0,则OB=3,
∴ 的半径为3;
【点睛】本题考查了圆周角定理,切线的判定,相似三角形的判定和性质;正确作出辅助线是解题关键.
23. 某文具店购进一批单价为12元的学习用品,按照相关部门规定其销售单价不低于进价,且不高于进价
的1.5倍,通过分析销售情况,发现每天的销售量y(件)与销售单价x(元)满足一次函数关系,且当
时, ;当 时, .
的
(1)求y与x之间 函数关系式;
(2)这种学习用品的销售单价定为多少时,每天可获得最大利润,最大利润是多少元?
【答案】(1)y与x之间的函数关系式为
(2)这种学习用品的销售单价定为16元时,每天可获得最大利润,最大利润是160元.
【解析】
【分析】(1)设y与x之间的函数关系式为 ,然后代值求解即可;
(2)设每天获得的利润为w元,由(1)可得 ,进而根据二次函数的性质可求解.
【小问1详解】
解:设y与x之间的函数关系式为 ,由题意得:
,解得: ,
∴y与x之间的函数关系式为 ;
【小问2详解】
解:设每天获得的利润为w元,由(1)可得:
第23页/共33页
学科网(北京)股份有限公司,
∵ ,且-10<0,
∴当 时,w有最大值,最大值为160;
答:这种学习用品的销售单价定为16元时,每天可获得最大利润,最大利润是160元.
【点睛】本题主要考查一次函数与二次函数的应用,熟练掌握一次函数与二次函数的图象与性质是解题的
关键.
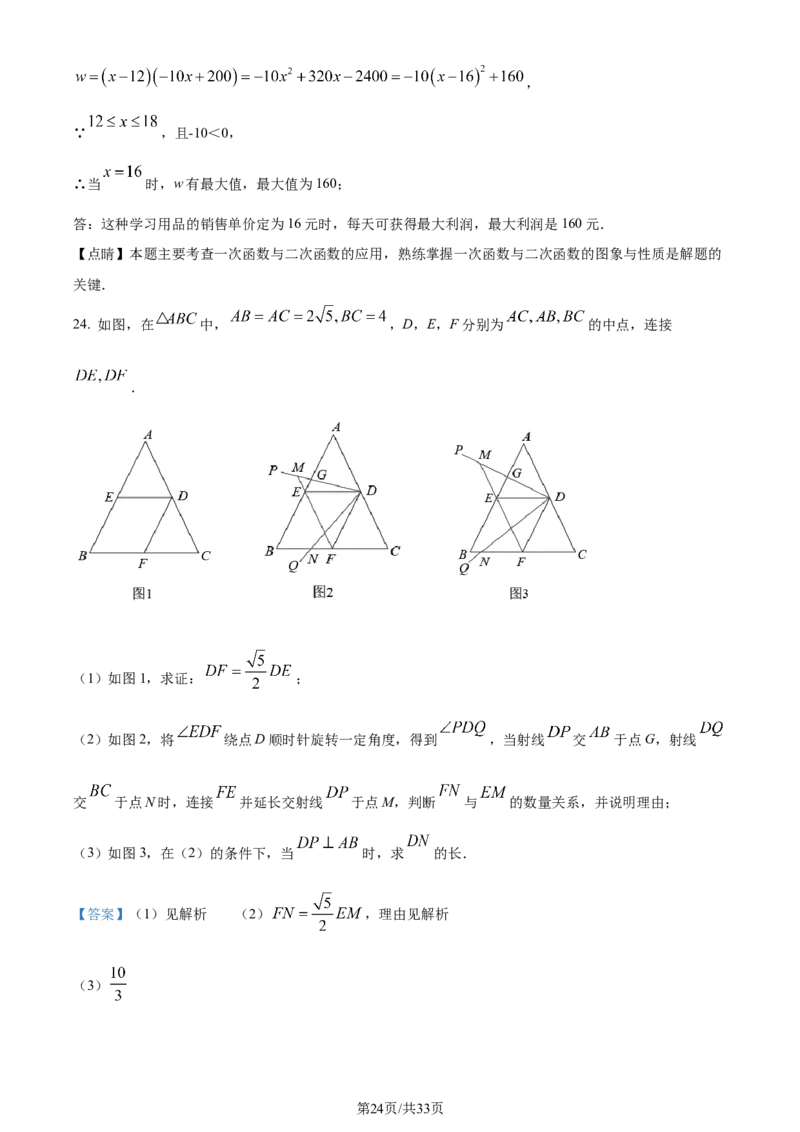
24. 如图,在 中, ,D,E,F分别为 的中点,连接
.
(1)如图1,求证: ;
(2)如图2,将 绕点D顺时针旋转一定角度,得到 ,当射线 交 于点G,射线
交 于点N时,连接 并延长交射线 于点M,判断 与 的数量关系,并说明理由;
(3)如图3,在(2)的条件下,当 时,求 的长.
【答案】(1)见解析 (2) ,理由见解析
(3)
第24页/共33页
学科网(北京)股份有限公司【解析】
【分析】(1)连接 ,可得 ,根据直角三角形斜边上的中线等于斜边的一半可得
,根据中位线定理可得 ,即可得证;
(2)证明 ,根据(1)的结论即可得 ;
(3)连接 ,过点 作 于 ,证明 ,可得 ,勾股定理
求得 ,根据 , ,可得 ,进而求
得 ,根据 求得 ,根据(2)的结论 ,即可求解.
【小问1详解】
证明:如图,连接 ,
,D,E,F分别为 的中点,
, ,
第25页/共33页
学科网(北京)股份有限公司,
,
【小问2详解】
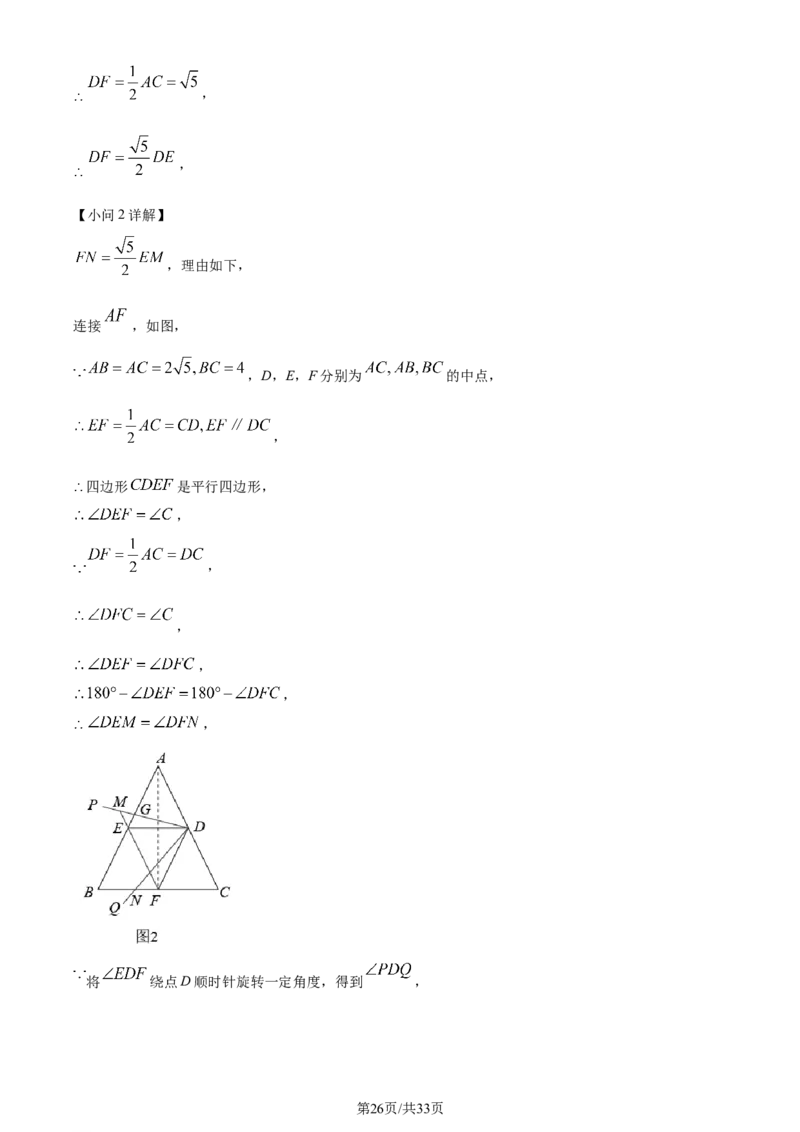
,理由如下,
连接 ,如图,
,D,E,F分别为 的中点,
,
四边形 是平行四边形,
,
,
,
,
,
,
将 绕点D顺时针旋转一定角度,得到 ,
第26页/共33页
学科网(北京)股份有限公司,
,
,
,
,
,
【小问3详解】
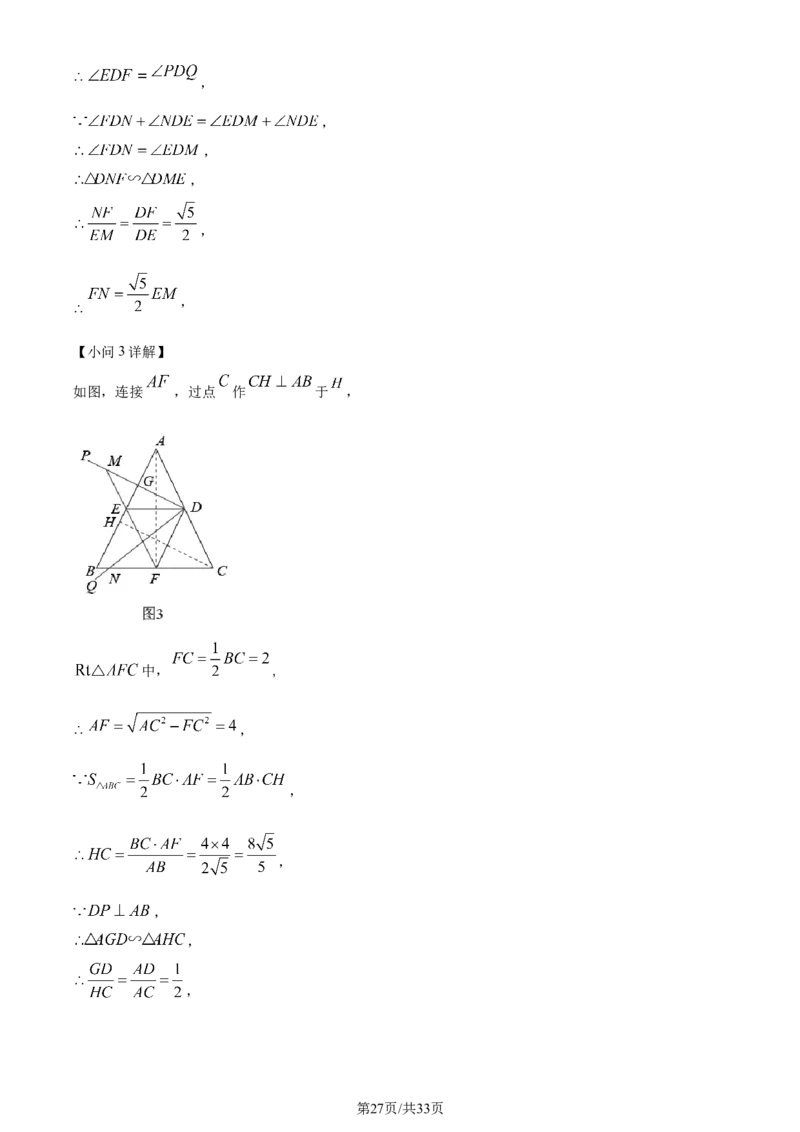
如图,连接 ,过点 作 于 ,
中, ,
,
,
,
,
,
,
第27页/共33页
学科网(北京)股份有限公司,
中,
,
中,
,
,
,
,
,
,
,
,
,
.
【点睛】本题考查了勾股定理,直角三角形斜边上的中线等于斜边的一半,中位线的性质定理,相似三角
形的性质与判定,求角的正确,掌握相似三角形的性质与判定是解题的关键.
第28页/共33页
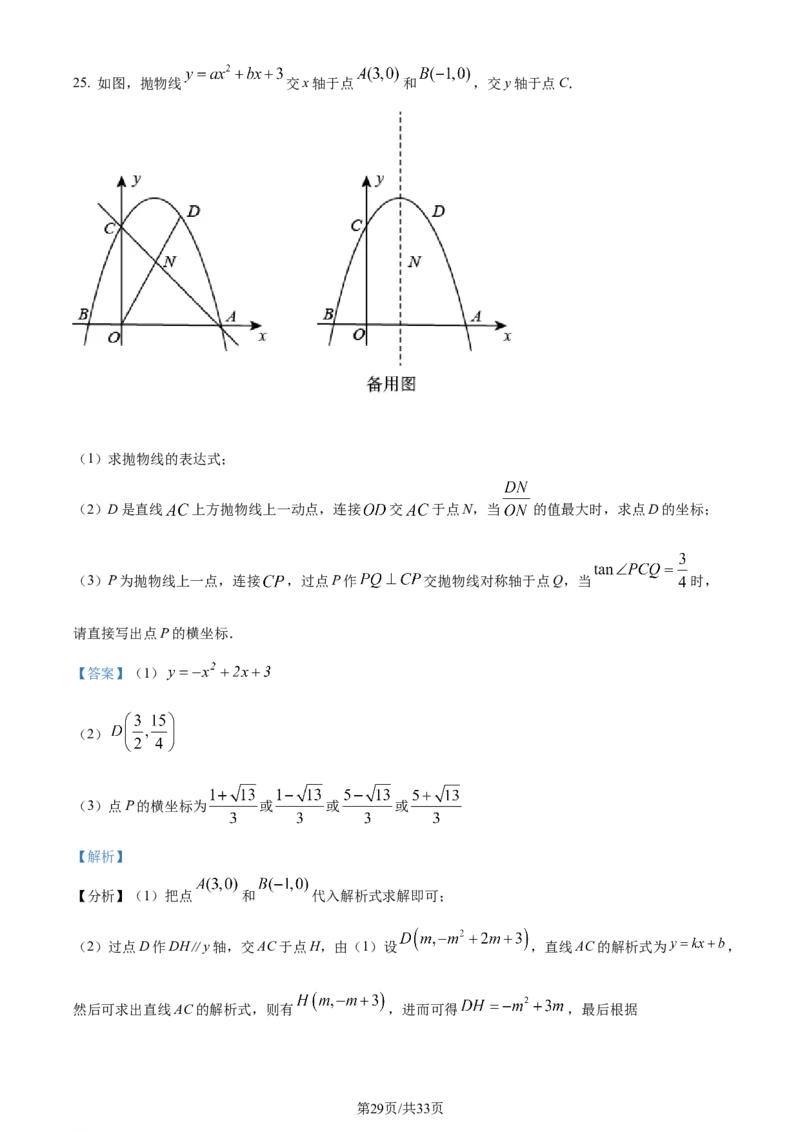
学科网(北京)股份有限公司25. 如图,抛物线 交x轴于点 和 ,交y轴于点C.
(1)求抛物线的表达式;
(2)D是直线 上方抛物线上一动点,连接 交 于点N,当 的值最大时,求点D的坐标;
(3)P为抛物线上一点,连接 ,过点P作 交抛物线对称轴于点Q,当 时,
请直接写出点P的横坐标.
【答案】(1)
(2)
(3)点P的横坐标为 或 或 或
【解析】
【分析】(1)把点 和 代入解析式求解即可;
(2)过点D作DH∥y轴,交AC于点H,由(1)设 ,直线AC的解析式为 ,
然后可求出直线AC的解析式,则有 ,进而可得 ,最后根据
第29页/共33页
学科网(北京)股份有限公司可进行求解;
(3)由题意可作出图象,设 ,然后根据题意及k型相似可进行求解.
【小问1详解】
解:把点 和 代入得:
,解得: ,
∴抛物线的解析式为 ;
【小问2详解】
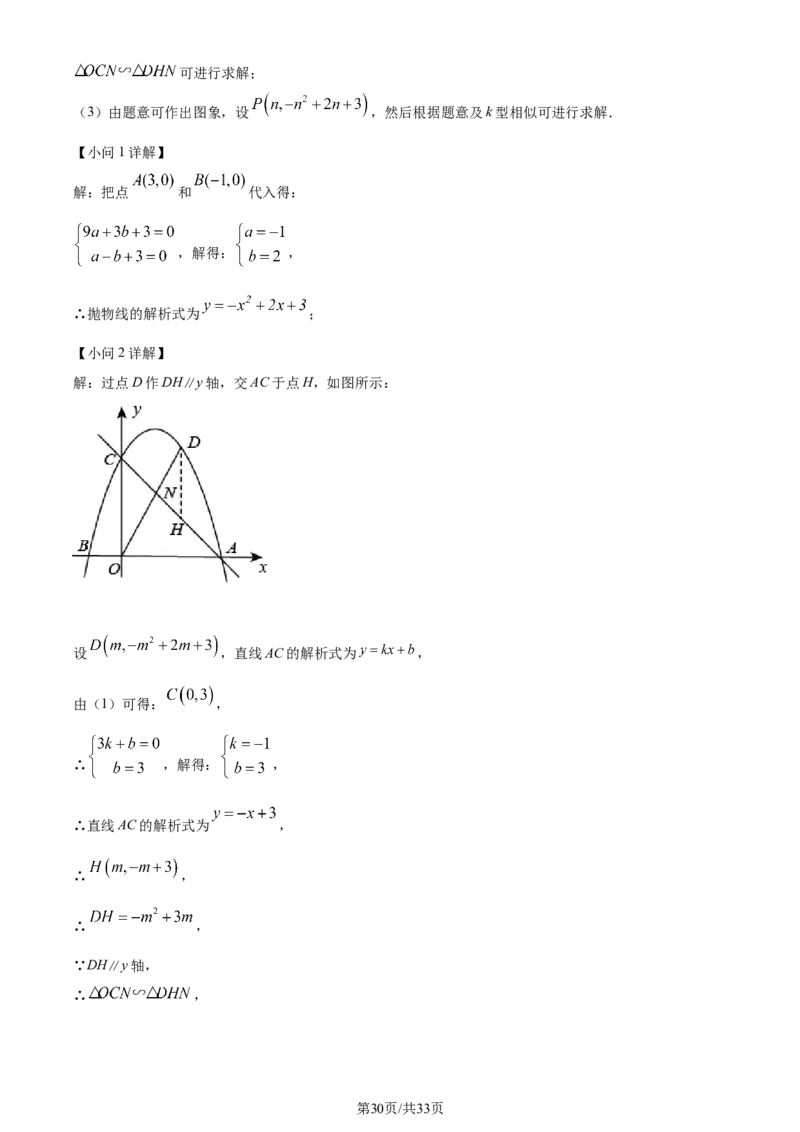
解:过点D作DH∥y轴,交AC于点H,如图所示:
设 ,直线AC的解析式为 ,
由(1)可得: ,
∴ ,解得: ,
∴直线AC的解析式为 ,
∴ ,
∴ ,
∵DH∥y轴,
∴ ,
第30页/共33页
学科网(北京)股份有限公司∴ ,
∵ ,
∴当 时, 的值最大,
∴ ;
【小问3详解】
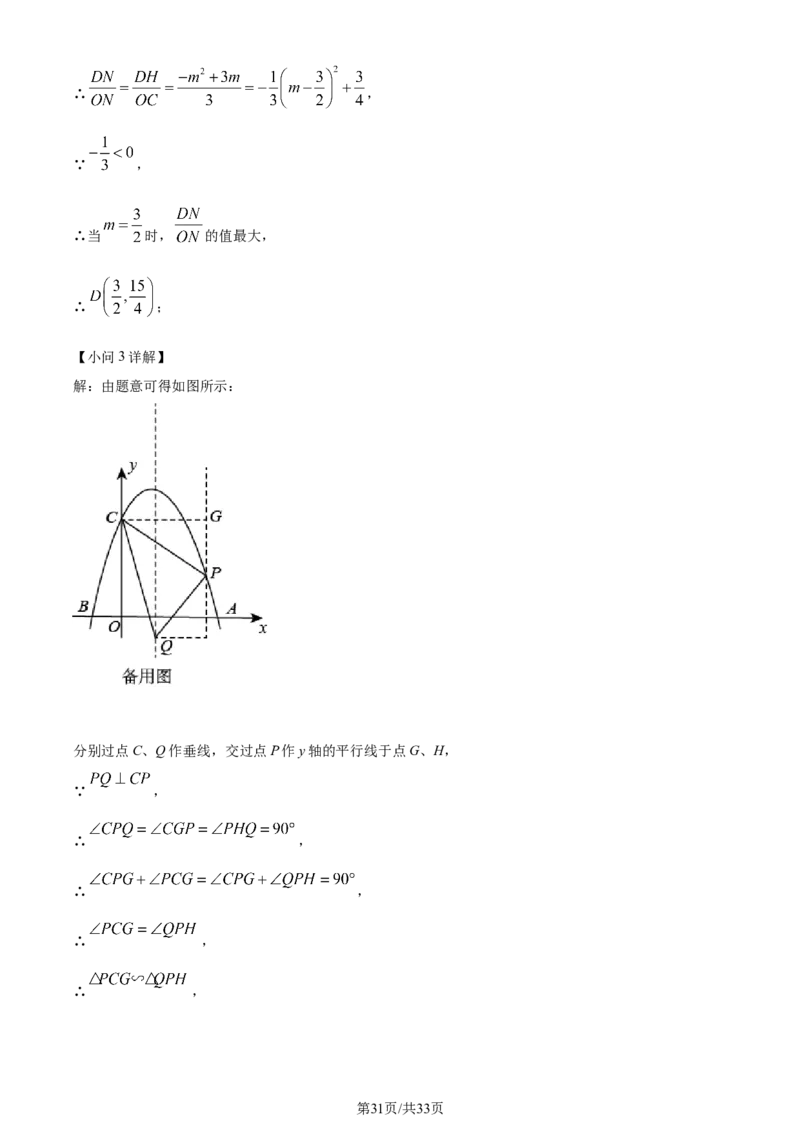
解:由题意可得如图所示:
分别过点C、Q作垂线,交过点P作y轴的平行线于点G、H,
∵ ,
∴ ,
∴ ,
∴ ,
∴ ,
第31页/共33页
学科网(北京)股份有限公司∴ ,
∵ ,
∴ ,
设点 ,由题意可知:抛物线的对称轴为直线 , ,
∴ ,
∴ ,
当 时,解得: ,
当 时,解得:
综上:点P的横坐标为 或 或 或 .
【点睛】本题主要考查二次函数的综合、三角函数及相似三角形的性质与判定,熟练掌握二次函数的综合、
三角函数及相似三角形的性质与判定是解题的关键.
第32页/共33页
学科网(北京)股份有限公司第33页/共33页
学科网(北京)股份有限公司