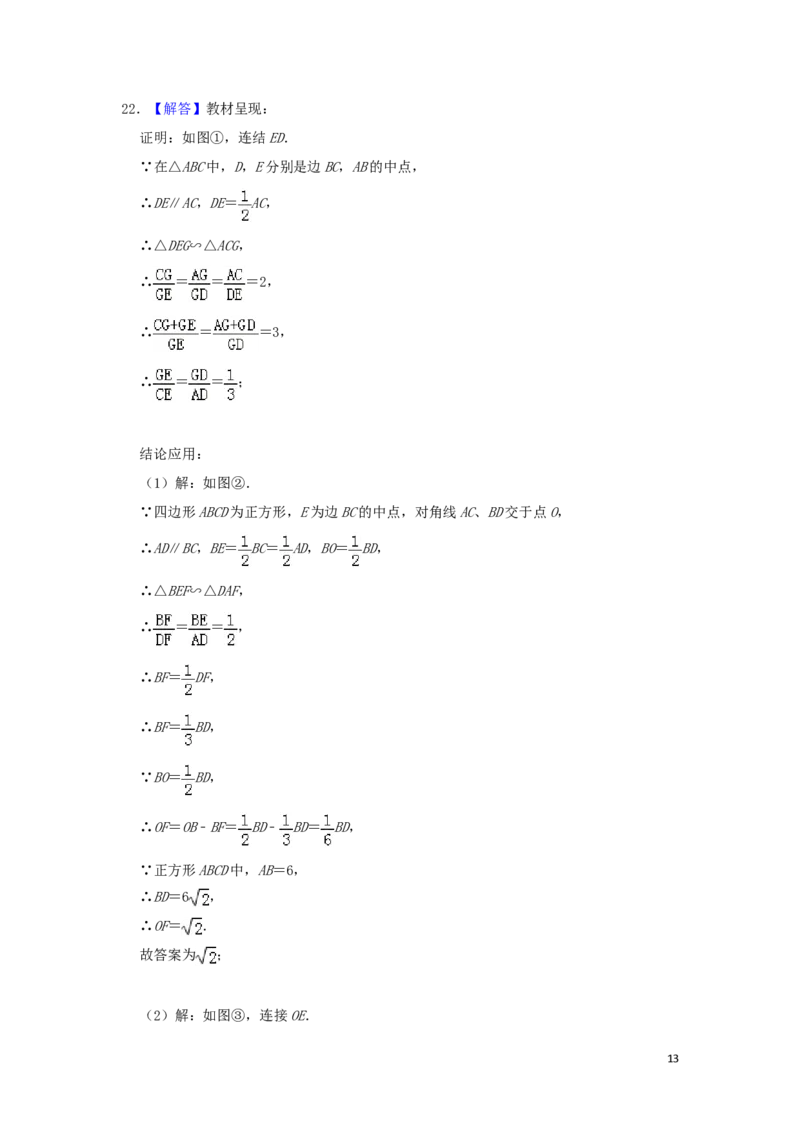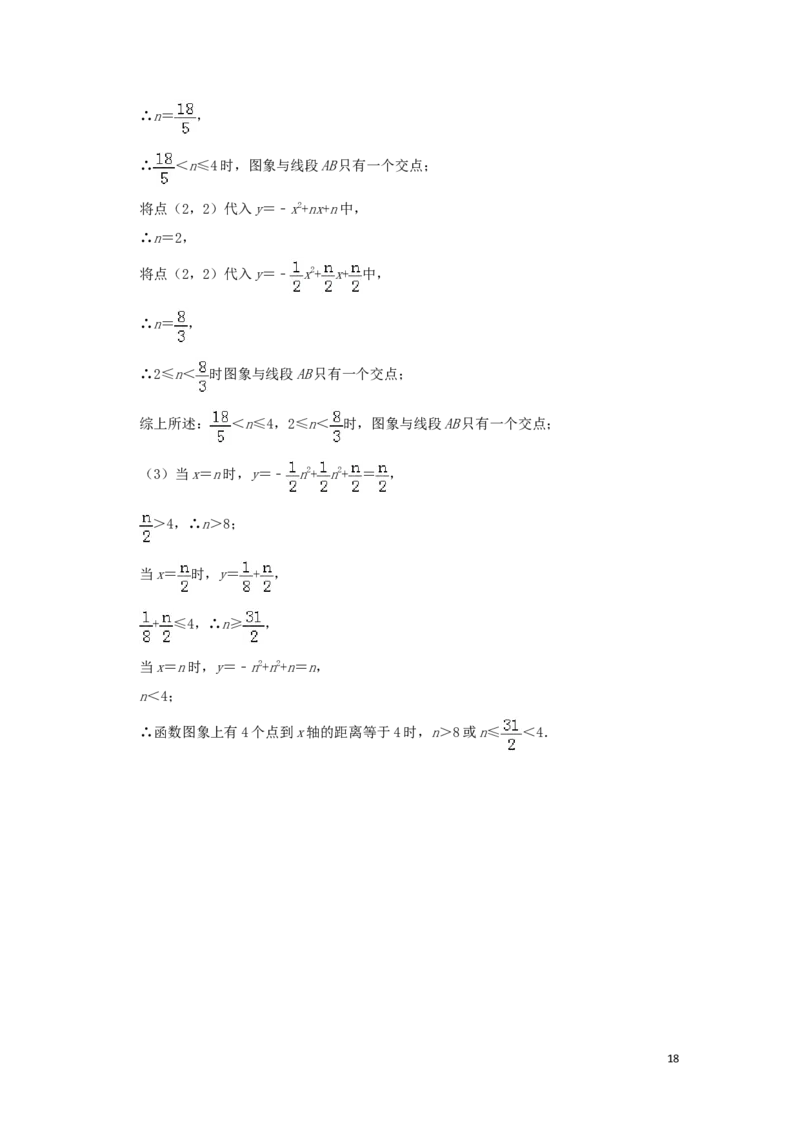文档内容
2019年吉林省长春市中考数学试卷
一、选择题(共8小题,每小题3分,满分24分)
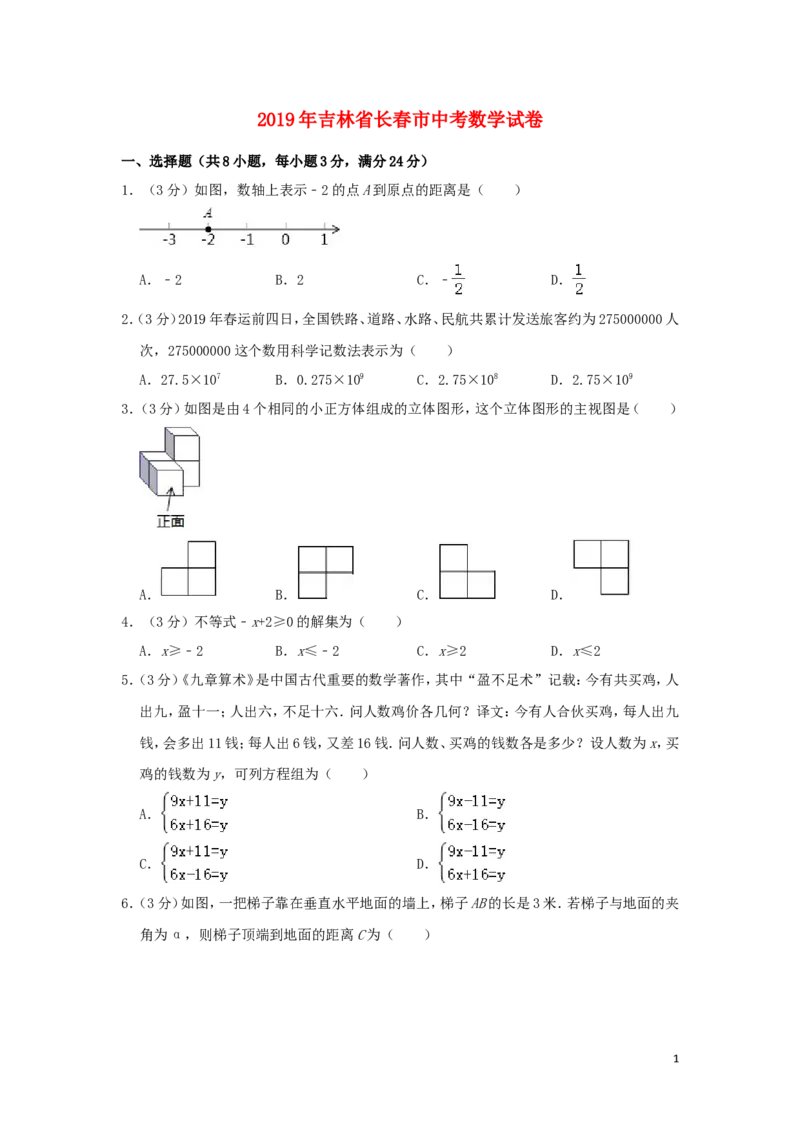
1.(3分)如图,数轴上表示﹣2的点A到原点的距离是( )
A.﹣2 B.2 C.﹣ D.
2.(3分)2019年春运前四日,全国铁路、道路、水路、民航共累计发送旅客约为275000000人
次,275000000这个数用科学记数法表示为( )
A.27.5×107 B.0.275×109 C.2.75×108 D.2.75×109
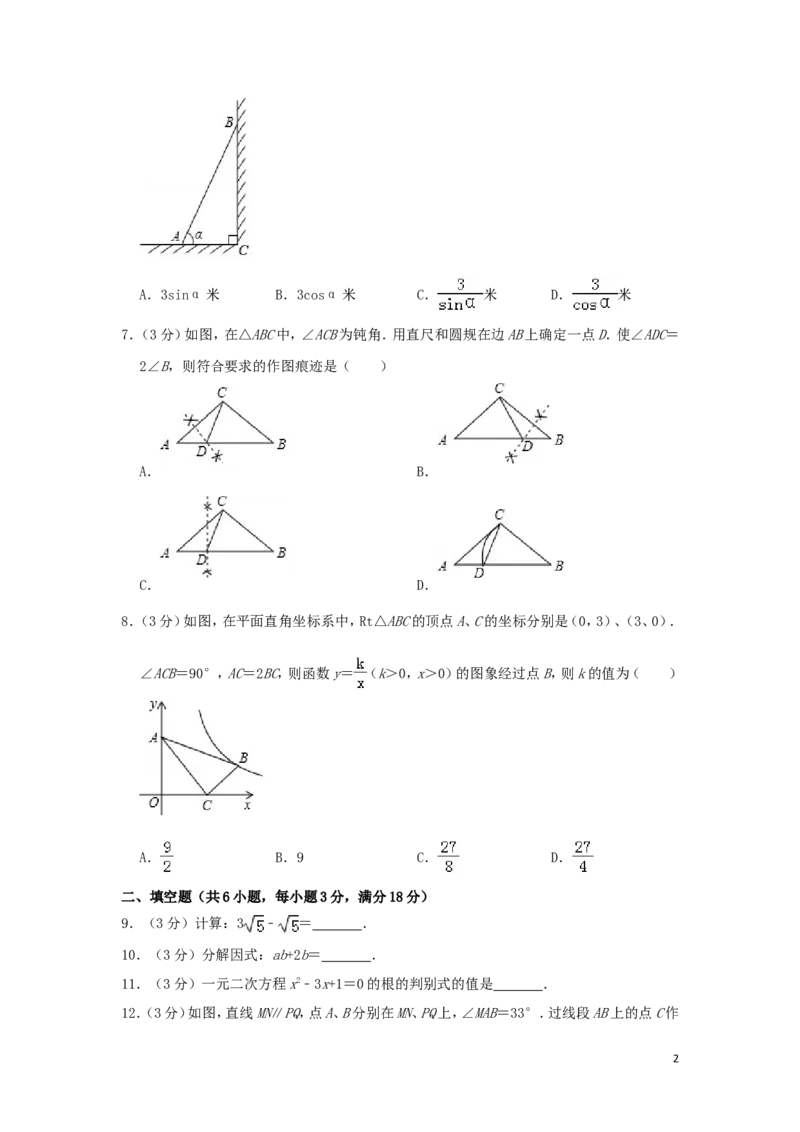
3.(3分)如图是由4个相同的小正方体组成的立体图形,这个立体图形的主视图是( )
A. B. C. D.
4.(3分)不等式﹣x+2≥0的解集为( )
A.x≥﹣2 B.x≤﹣2 C.x≥2 D.x≤2
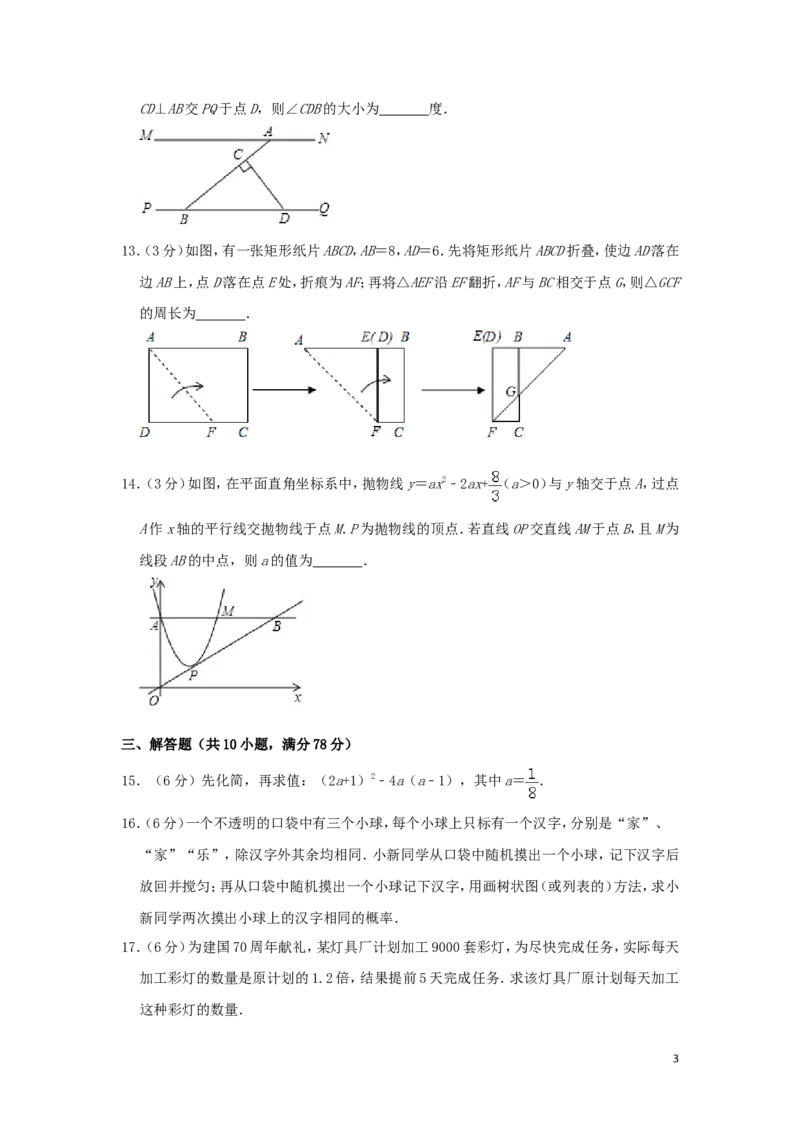
5.(3分)《九章算术》是中国古代重要的数学著作,其中“盈不足术”记载:今有共买鸡,人
出九,盈十一;人出六,不足十六.问人数鸡价各几何?译文:今有人合伙买鸡,每人出九
钱,会多出11钱;每人出6钱,又差16钱.问人数、买鸡的钱数各是多少?设人数为x,买
鸡的钱数为y,可列方程组为( )
A. B.
C. D.
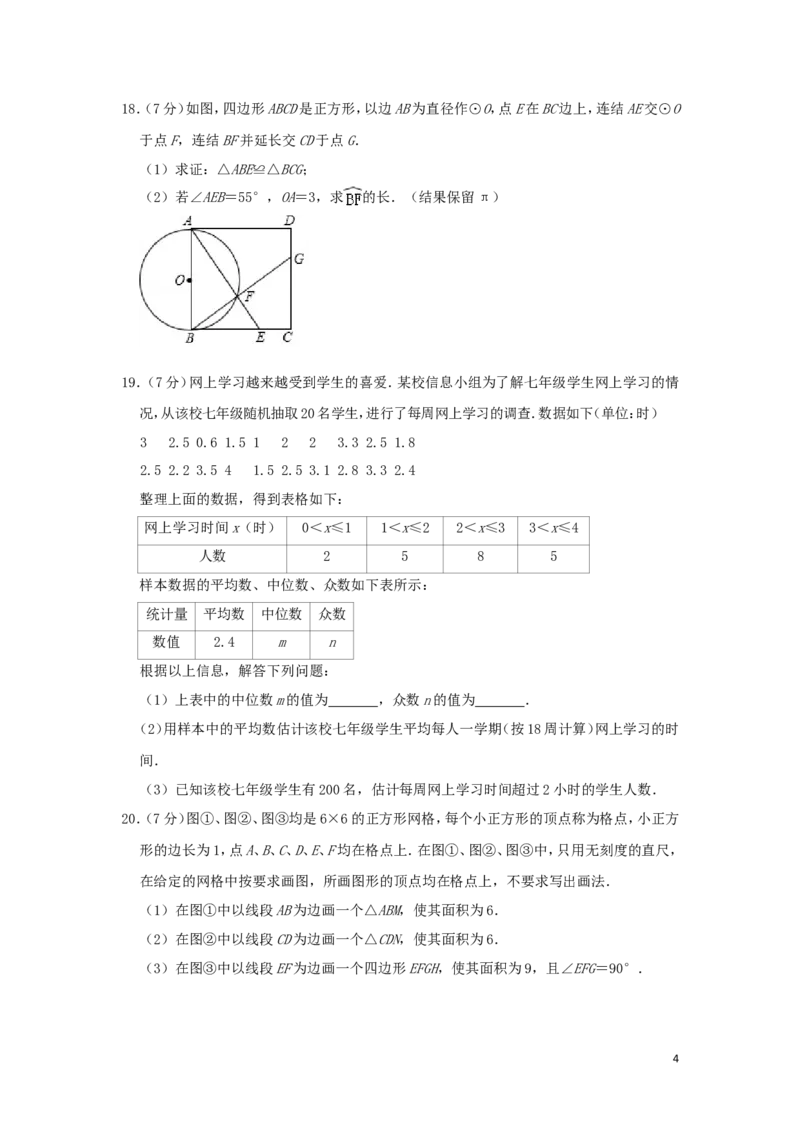
6.(3分)如图,一把梯子靠在垂直水平地面的墙上,梯子AB的长是3米.若梯子与地面的夹
角为α,则梯子顶端到地面的距离C为( )
1A.3sinα米 B.3cosα米 C. 米 D. 米
7.(3分)如图,在△ABC中,∠ACB为钝角.用直尺和圆规在边AB上确定一点D.使∠ADC=
2∠B,则符合要求的作图痕迹是( )
A. B.
C. D.
8.(3分)如图,在平面直角坐标系中,Rt△ABC的顶点A、C的坐标分别是(0,3)、(3、0).
∠ACB=90°,AC=2BC,则函数y= (k>0,x>0)的图象经过点B,则k的值为( )
A. B.9 C. D.
二、填空题(共6小题,每小题3分,满分18分)
9.(3分)计算:3 ﹣ = .
10.(3分)分解因式:ab+2b= .
11.(3分)一元二次方程x2﹣3x+1=0的根的判别式的值是 .
12.(3分)如图,直线MN∥PQ,点A、B分别在MN、PQ上,∠MAB=33°.过线段AB上的点C作
2CD⊥AB交PQ于点D,则∠CDB的大小为 度.
13.(3分)如图,有一张矩形纸片ABCD,AB=8,AD=6.先将矩形纸片ABCD折叠,使边AD落在
边AB上,点D落在点E处,折痕为AF;再将△AEF沿EF翻折,AF与BC相交于点G,则△GCF
的周长为 .
14.(3分)如图,在平面直角坐标系中,抛物线y=ax2﹣2ax+ (a>0)与y轴交于点A,过点
A作x轴的平行线交抛物线于点M.P为抛物线的顶点.若直线OP交直线AM于点B,且M为
线段AB的中点,则a的值为 .
三、解答题(共10小题,满分78分)
15.(6分)先化简,再求值:(2a+1)2﹣4a(a﹣1),其中a= .
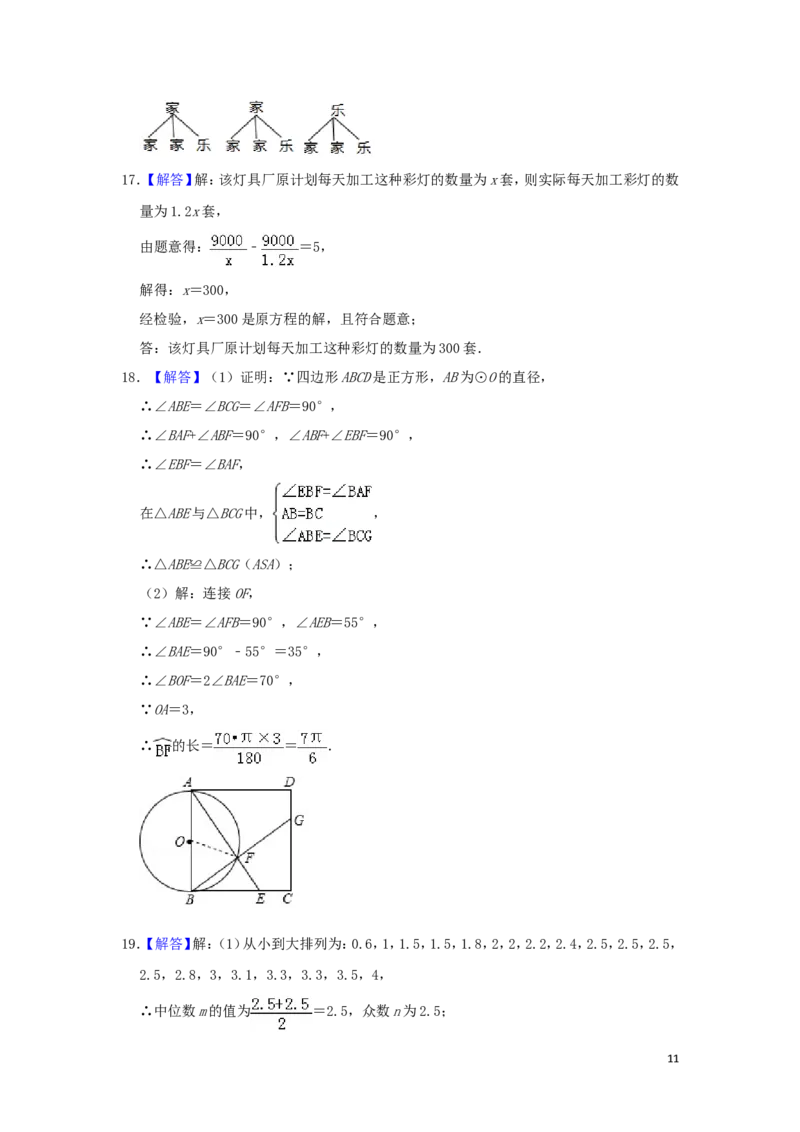
16.(6分)一个不透明的口袋中有三个小球,每个小球上只标有一个汉字,分别是“家”、
“家”“乐”,除汉字外其余均相同.小新同学从口袋中随机摸出一个小球,记下汉字后
放回并搅匀;再从口袋中随机摸出一个小球记下汉字,用画树状图(或列表的)方法,求小
新同学两次摸出小球上的汉字相同的概率.
17.(6分)为建国70周年献礼,某灯具厂计划加工9000套彩灯,为尽快完成任务,实际每天
加工彩灯的数量是原计划的1.2倍,结果提前5天完成任务.求该灯具厂原计划每天加工
这种彩灯的数量.
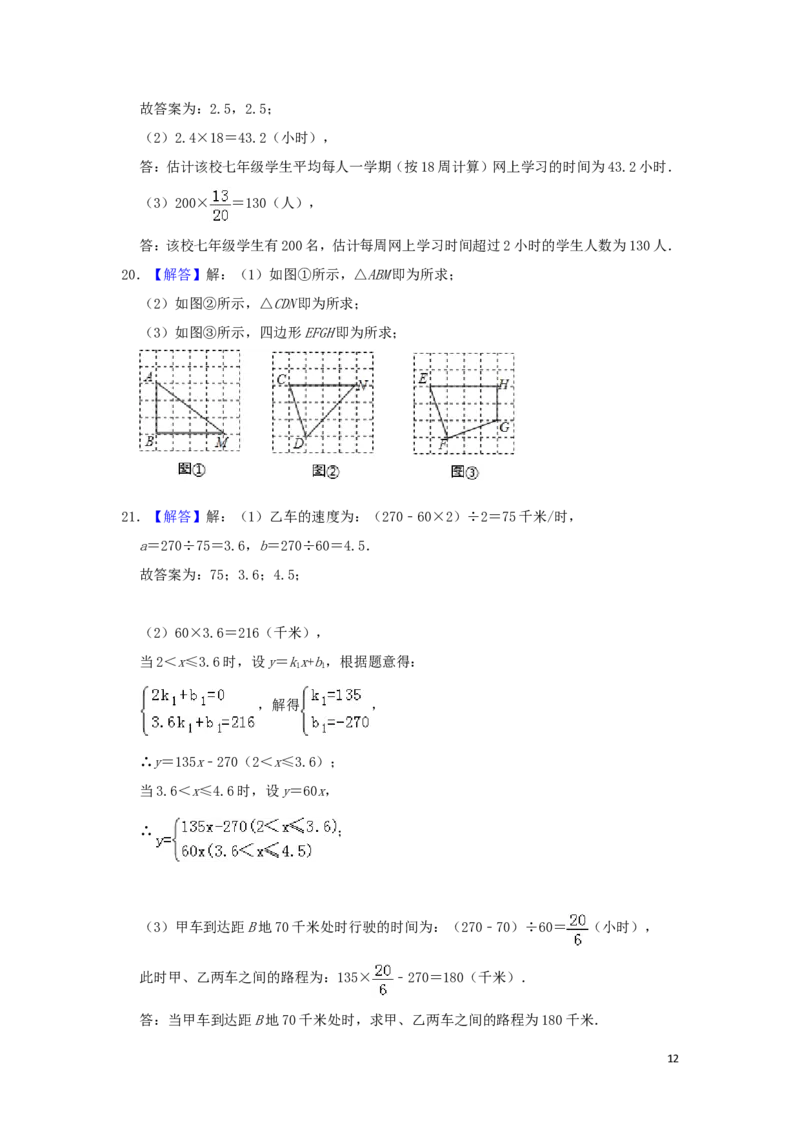
318.(7分)如图,四边形ABCD是正方形,以边AB为直径作⊙O,点E在BC边上,连结AE交⊙O
于点F,连结BF并延长交CD于点G.
(1)求证:△ABE≌△BCG;
(2)若∠AEB=55°,OA=3,求 的长.(结果保留π)
19.(7分)网上学习越来越受到学生的喜爱.某校信息小组为了解七年级学生网上学习的情
况,从该校七年级随机抽取20名学生,进行了每周网上学习的调查.数据如下(单位:时)
3 2.5 0.6 1.5 1 2 2 3.3 2.5 1.8
2.5 2.2 3.5 4 1.5 2.5 3.1 2.8 3.3 2.4
整理上面的数据,得到表格如下:
网上学习时间x(时) 0<x≤1 1<x≤2 2<x≤3 3<x≤4
人数 2 5 8 5
样本数据的平均数、中位数、众数如下表所示:
统计量 平均数 中位数 众数
数值 2.4 m n
根据以上信息,解答下列问题:
(1)上表中的中位数m的值为 ,众数n的值为 .
(2)用样本中的平均数估计该校七年级学生平均每人一学期(按18周计算)网上学习的时
间.
(3)已知该校七年级学生有200名,估计每周网上学习时间超过2小时的学生人数.
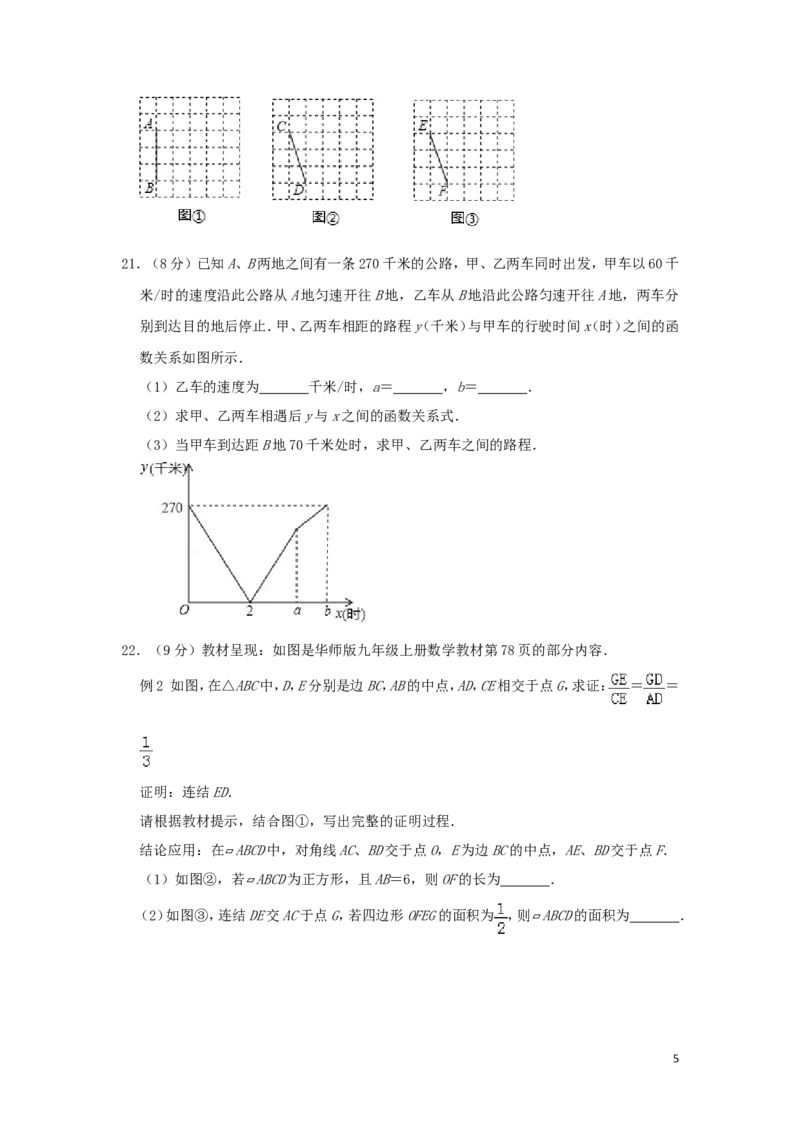
20.(7分)图①、图②、图③均是6×6的正方形网格,每个小正方形的顶点称为格点,小正方
形的边长为1,点A、B、C、D、E、F均在格点上.在图①、图②、图③中,只用无刻度的直尺,
在给定的网格中按要求画图,所画图形的顶点均在格点上,不要求写出画法.
(1)在图①中以线段AB为边画一个△ABM,使其面积为6.
(2)在图②中以线段CD为边画一个△CDN,使其面积为6.
(3)在图③中以线段EF为边画一个四边形EFGH,使其面积为9,且∠EFG=90°.
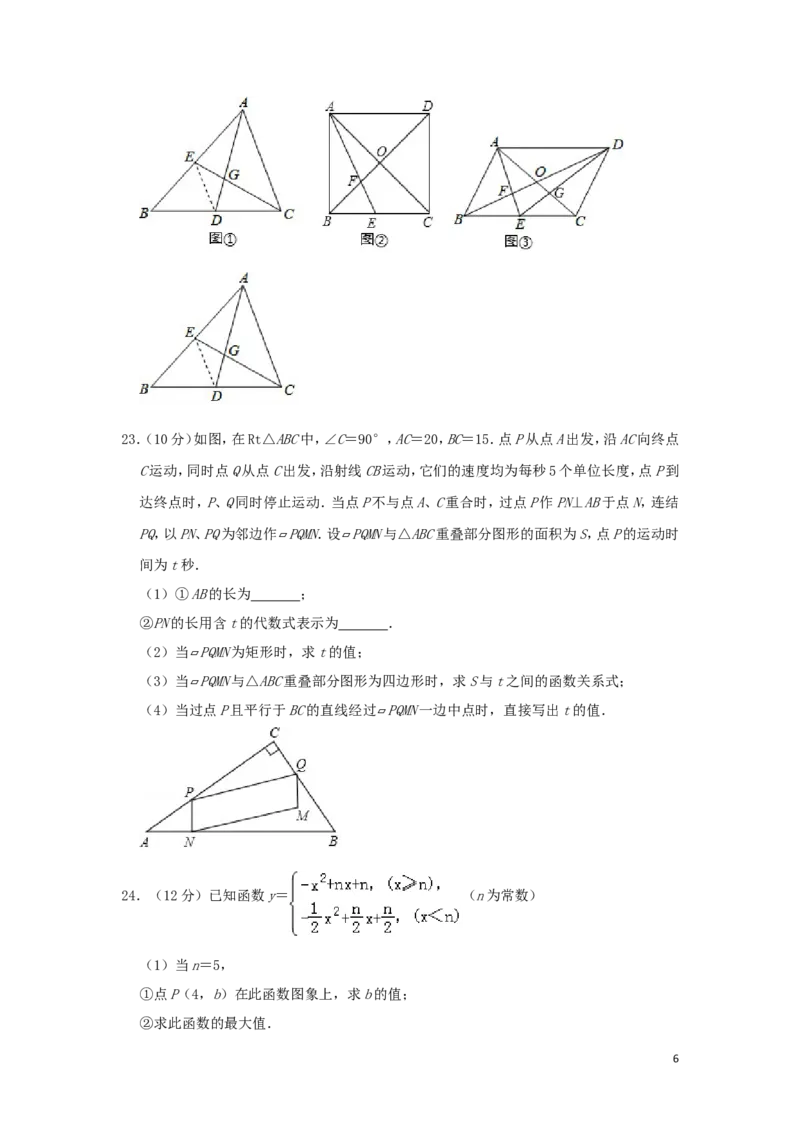
421.(8分)已知A、B两地之间有一条270千米的公路,甲、乙两车同时出发,甲车以60千
米/时的速度沿此公路从A地匀速开往B地,乙车从B地沿此公路匀速开往A地,两车分
别到达目的地后停止.甲、乙两车相距的路程y(千米)与甲车的行驶时间x(时)之间的函
数关系如图所示.
(1)乙车的速度为 千米/时,a= ,b= .
(2)求甲、乙两车相遇后y与x之间的函数关系式.
(3)当甲车到达距B地70千米处时,求甲、乙两车之间的路程.
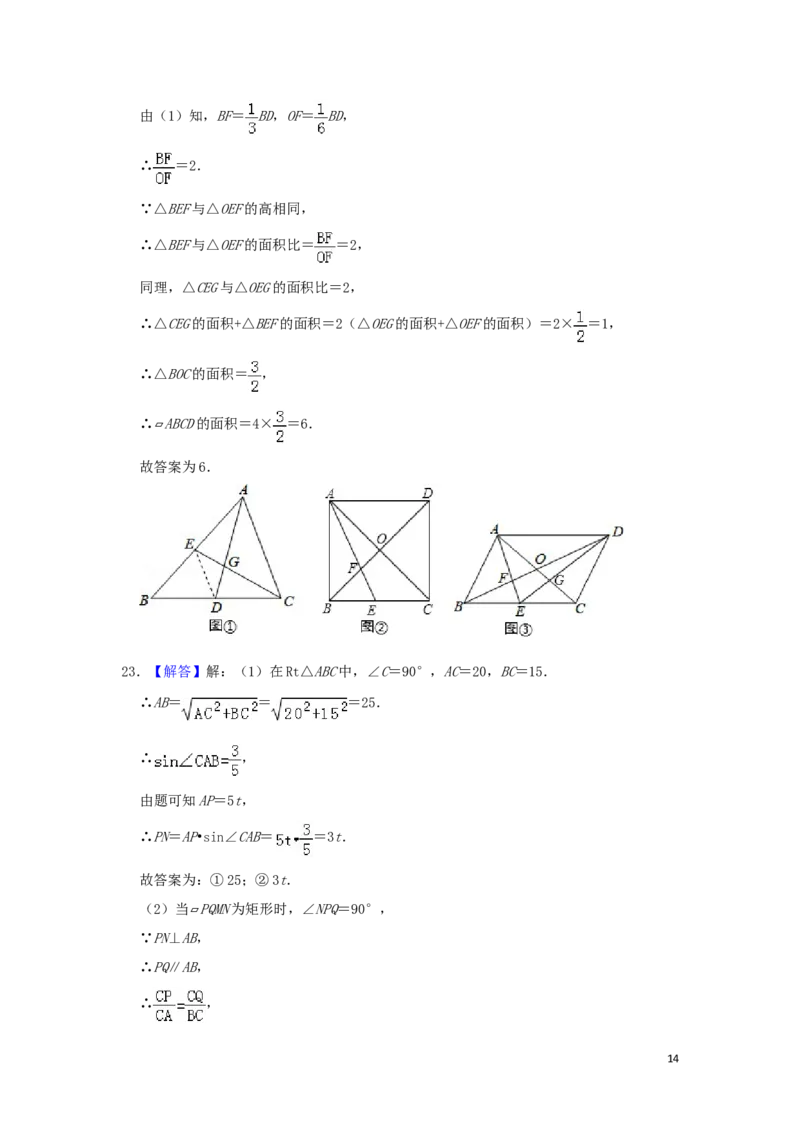
22.(9分)教材呈现:如图是华师版九年级上册数学教材第78页的部分内容.
例2 如图,在△ABC中,D,E分别是边BC,AB的中点,AD,CE相交于点G,求证: = =
证明:连结ED.
请根据教材提示,结合图①,写出完整的证明过程.
结论应用:在 ABCD中,对角线AC、BD交于点O,E为边BC的中点,AE、BD交于点F.
▱
(1)如图②,若 ABCD为正方形,且AB=6,则OF的长为 .
▱
(2)如图③,连结DE交AC于点G,若四边形OFEG的面积为 ,则 ABCD的面积为 .
▱
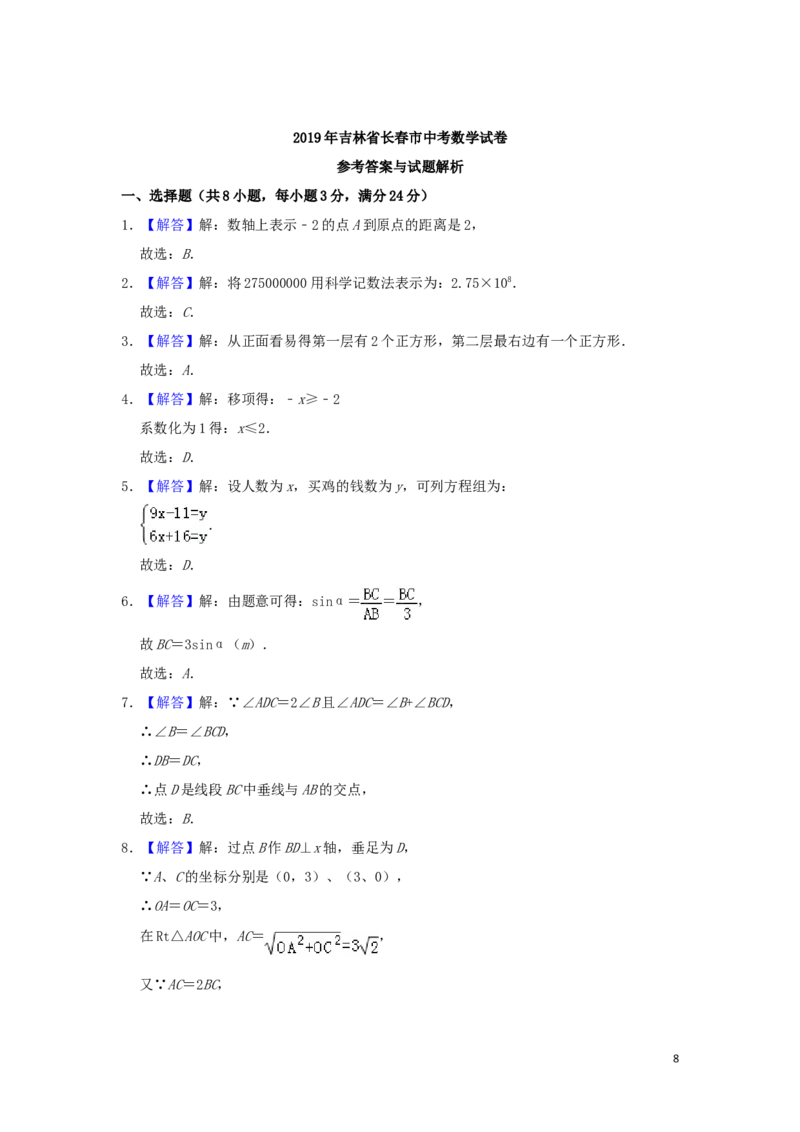
523.(10分)如图,在Rt△ABC中,∠C=90°,AC=20,BC=15.点P从点A出发,沿AC向终点
C运动,同时点Q从点C出发,沿射线CB运动,它们的速度均为每秒5个单位长度,点P到
达终点时,P、Q同时停止运动.当点P不与点A、C重合时,过点P作PN⊥AB于点N,连结
PQ,以PN、PQ为邻边作 PQMN.设 PQMN与△ABC重叠部分图形的面积为S,点P的运动时
▱ ▱
间为t秒.
(1)①AB的长为 ;
②PN的长用含t的代数式表示为 .
(2)当 PQMN为矩形时,求t的值;
▱
(3)当 PQMN与△ABC重叠部分图形为四边形时,求S与t之间的函数关系式;
▱
(4)当过点P且平行于BC的直线经过 PQMN一边中点时,直接写出t的值.
▱
24.(12分)已知函数y= (n为常数)
(1)当n=5,
①点P(4,b)在此函数图象上,求b的值;
②求此函数的最大值.
6(2)已知线段AB的两个端点坐标分别为A(2,2)、B(4,2),当此函数的图象与线段AB只
有一个交点时,直接写出n的取值范围.
(3)当此函数图象上有4个点到x轴的距离等于4,求n的取值范围.
72019年吉林省长春市中考数学试卷
参考答案与试题解析
一、选择题(共8小题,每小题3分,满分24分)
1.【解答】解:数轴上表示﹣2的点A到原点的距离是2,
故选:B.
2.【解答】解:将275000000用科学记数法表示为:2.75×108.
故选:C.
3.【解答】解:从正面看易得第一层有2个正方形,第二层最右边有一个正方形.
故选:A.
4.【解答】解:移项得:﹣x≥﹣2
系数化为1得:x≤2.
故选:D.
5.【解答】解:设人数为x,买鸡的钱数为y,可列方程组为:
.
故选:D.
6.【解答】解:由题意可得:sinα= = ,
故BC=3sinα(m).
故选:A.
7.【解答】解:∵∠ADC=2∠B且∠ADC=∠B+∠BCD,
∴∠B=∠BCD,
∴DB=DC,
∴点D是线段BC中垂线与AB的交点,
故选:B.
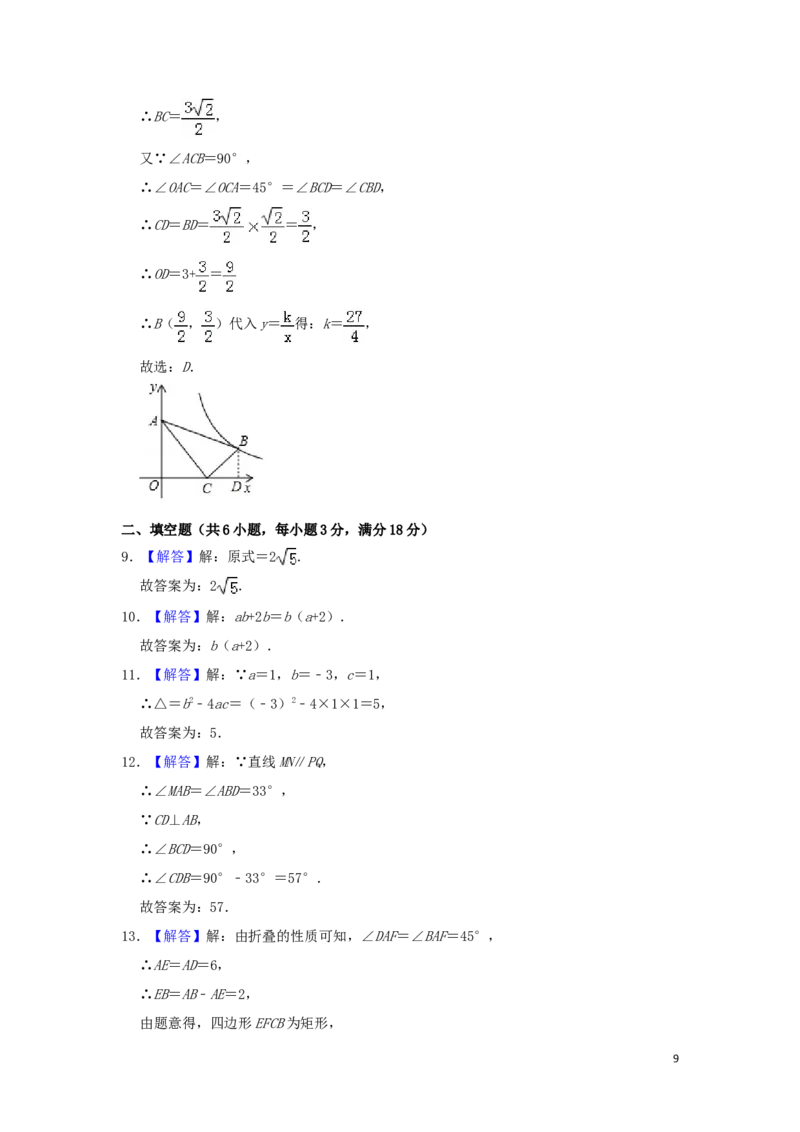
8.【解答】解:过点B作BD⊥x轴,垂足为D,
∵A、C的坐标分别是(0,3)、(3、0),
∴OA=OC=3,
在Rt△AOC中,AC= ,
又∵AC=2BC,
8∴BC= ,
又∵∠ACB=90°,
∴∠OAC=∠OCA=45°=∠BCD=∠CBD,
∴CD=BD= = ,
∴OD=3+ =
∴B( , )代入y= 得:k= ,
故选:D.
二、填空题(共6小题,每小题3分,满分18分)
9.【解答】解:原式=2 .
故答案为:2 .
10.【解答】解:ab+2b=b(a+2).
故答案为:b(a+2).
11.【解答】解:∵a=1,b=﹣3,c=1,
∴△=b2﹣4ac=(﹣3)2﹣4×1×1=5,
故答案为:5.
12.【解答】解:∵直线MN∥PQ,
∴∠MAB=∠ABD=33°,
∵CD⊥AB,
∴∠BCD=90°,
∴∠CDB=90°﹣33°=57°.
故答案为:57.
13.【解答】解:由折叠的性质可知,∠DAF=∠BAF=45°,
∴AE=AD=6,
∴EB=AB﹣AE=2,
由题意得,四边形EFCB为矩形,
9∴FC=ED=2,
∵AB∥FC,
∴∠GFC=∠A=45°,
∴GC=FC=2,
由勾股定理得,GF= =2 ,
则△GCF的周长=GC+FC+GF=4+2 ,
故答案为:4+2 .
14.【解答】解:∵抛物线y=ax2﹣2ax+ (a>0)与y轴交于点A,
∴A(0, ),抛物线的对称轴为x=1
∴顶点P坐标为(1, ﹣a),点M坐标为(2, )
∵点M为线段AB的中点,
∴点B坐标为(4, )
设直线OP解析式为y=kx(k为常数,且k≠0)
将点P(1, )代入得 =k
∴y=( )x
将点B(4, )代入得 =( )×4
解得a=2
故答案为:2.
三、解答题(共10小题,满分78分)
15.【解答】解:原式=4a2+4a+1﹣4a2+4a
=8a+1,
当a= 时,原式=8a+1=2.
16.【解答】解:画树状图如图:
共有9个等可能的结果,小新同学两次摸出小球上的汉字相同的结果有5个,
∴小新同学两次摸出小球上的汉字相同的概率为 .
1017.【解答】解:该灯具厂原计划每天加工这种彩灯的数量为x套,则实际每天加工彩灯的数
量为1.2x套,
由题意得: ﹣ =5,
解得:x=300,
经检验,x=300是原方程的解,且符合题意;
答:该灯具厂原计划每天加工这种彩灯的数量为300套.
18.【解答】(1)证明:∵四边形ABCD是正方形,AB为⊙O的直径,
∴∠ABE=∠BCG=∠AFB=90°,
∴∠BAF+∠ABF=90°,∠ABF+∠EBF=90°,
∴∠EBF=∠BAF,
在△ABE与△BCG中, ,
∴△ABE≌△BCG(ASA);
(2)解:连接OF,
∵∠ABE=∠AFB=90°,∠AEB=55°,
∴∠BAE=90°﹣55°=35°,
∴∠BOF=2∠BAE=70°,
∵OA=3,
∴ 的长= = .
19.【解答】解:(1)从小到大排列为:0.6,1,1.5,1.5,1.8,2,2,2.2,2.4,2.5,2.5,2.5,
2.5,2.8,3,3.1,3.3,3.3,3.5,4,
∴中位数m的值为 =2.5,众数n为2.5;
11故答案为:2.5,2.5;
(2)2.4×18=43.2(小时),
答:估计该校七年级学生平均每人一学期(按18周计算)网上学习的时间为43.2小时.
(3)200× =130(人),
答:该校七年级学生有200名,估计每周网上学习时间超过2小时的学生人数为130人.
20.【解答】解:(1)如图①所示,△ABM即为所求;
(2)如图②所示,△CDN即为所求;
(3)如图③所示,四边形EFGH即为所求;
21.【解答】解:(1)乙车的速度为:(270﹣60×2)÷2=75千米/时,
a=270÷75=3.6,b=270÷60=4.5.
故答案为:75;3.6;4.5;
(2)60×3.6=216(千米),
当2<x≤3.6时,设y=kx+b,根据题意得:
1 1
,解得 ,
∴y=135x﹣270(2<x≤3.6);
当3.6<x≤4.6时,设y=60x,
∴ ;
(3)甲车到达距B地70千米处时行驶的时间为:(270﹣70)÷60= (小时),
此时甲、乙两车之间的路程为:135× ﹣270=180(千米).
答:当甲车到达距B地70千米处时,求甲、乙两车之间的路程为180千米.
1222.【解答】教材呈现:
证明:如图①,连结ED.
∵在△ABC中,D,E分别是边BC,AB的中点,
∴DE∥AC,DE= AC,
∴△DEG∽△ACG,
∴ = = =2,
∴ = =3,
∴ = = ;
结论应用:
(1)解:如图②.
∵四边形ABCD为正方形,E为边BC的中点,对角线AC、BD交于点O,
∴AD∥BC,BE= BC= AD,BO= BD,
∴△BEF∽△DAF,
∴ = = ,
∴BF= DF,
∴BF= BD,
∵BO= BD,
∴OF=OB﹣BF= BD﹣ BD= BD,
∵正方形ABCD中,AB=6,
∴BD=6 ,
∴OF= .
故答案为 ;
(2)解:如图③,连接OE.
13由(1)知,BF= BD,OF= BD,
∴ =2.
∵△BEF与△OEF的高相同,
∴△BEF与△OEF的面积比= =2,
同理,△CEG与△OEG的面积比=2,
∴△CEG的面积+△BEF的面积=2(△OEG的面积+△OEF的面积)=2× =1,
∴△BOC的面积= ,
∴ ABCD的面积=4× =6.
▱
故答案为6.
23.【解答】解:(1)在Rt△ABC中,∠C=90°,AC=20,BC=15.
∴AB= = =25.
∴ ,
由题可知AP=5t,
∴PN=AP•sin∠CAB= =3t.
故答案为:①25;②3t.
(2)当 PQMN为矩形时,∠NPQ=90°,
▱
∵PN⊥AB,
∴PQ∥AB,
∴ ,
14由题意可知AP=CQ=5t,CP=20﹣5t,
∴ ,
解得t= ,
即当 PQMN为矩形时t= .
▱
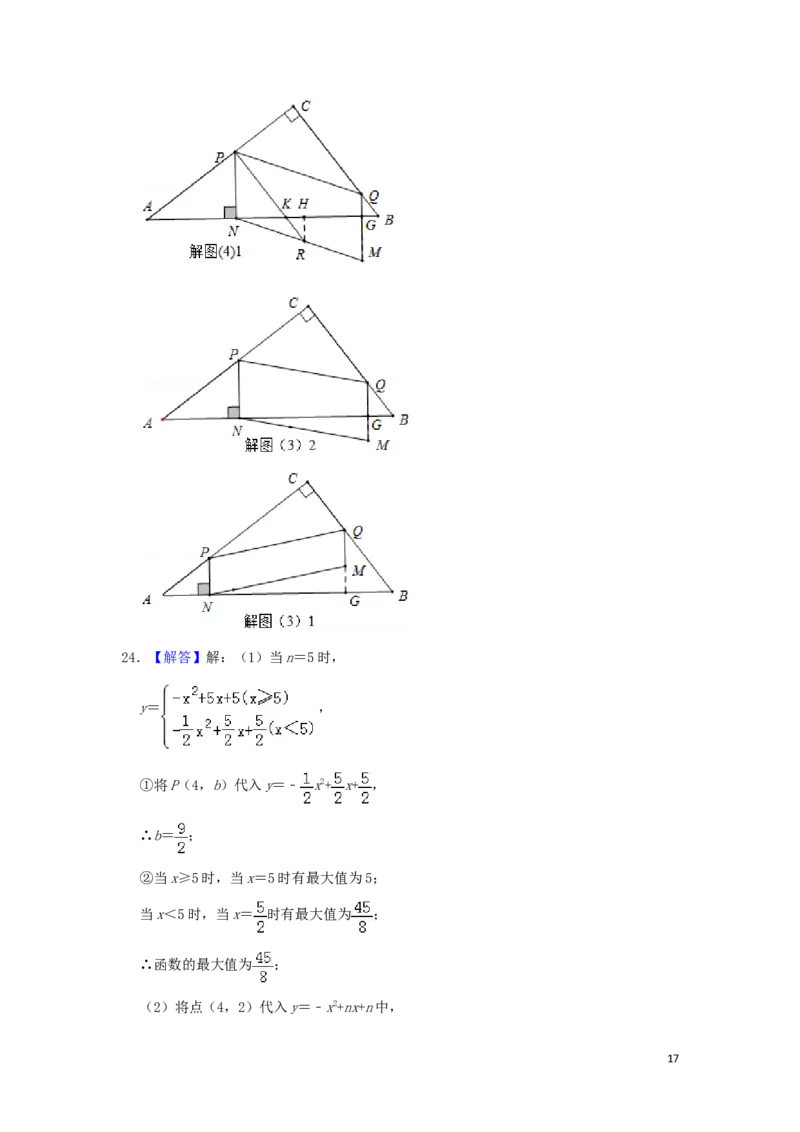
(3)当 PQMN△ABC重叠部分图形为四边形时,有两种情况,
▱
Ⅰ.如解图(3)1所示. PQMN在三角形内部时.延长QM交AB于G点,
▱
由(1)题可知:cosA=sinB= ,cosB= ,AP=5t,BQ=15﹣5t,PN=QM=3t.
∴AN=AP•cosA=4t,BG=BQ•cosB=9﹣3t,QG=BQ•sinB=12﹣4t,
∵. PQMN在三角形内部时.有0<QM≤QG,
▱
∴0<3t≤12﹣4t,
∴0<t .
∴NG=25﹣4t﹣(9﹣3t)=16﹣t.
∴当0<t 时, PQMN与△ABC重叠部分图形为 PQMN,S与t之间的函数关系式为S
▱ ▱
=PN•NG=3t•(16﹣t)=﹣3t2+48t.
Ⅱ.如解图(3)2所示.当0<QG<QM, PQMN与△ABC重叠部分图形为梯形PQMG时,
▱
即:0<12﹣4t<3t,解得: ,
PQMN 与 △ ABC 重 叠 部 分 图 形 为 梯 形 PQMG 的 面 积 S= =
▱
= .
综上所述:当0<t 时,S=﹣3t2+48t.当 ,S= .
(4)当过点P且平行于BC的直线经过 PQMN一边中点时,有两种情况,
▱
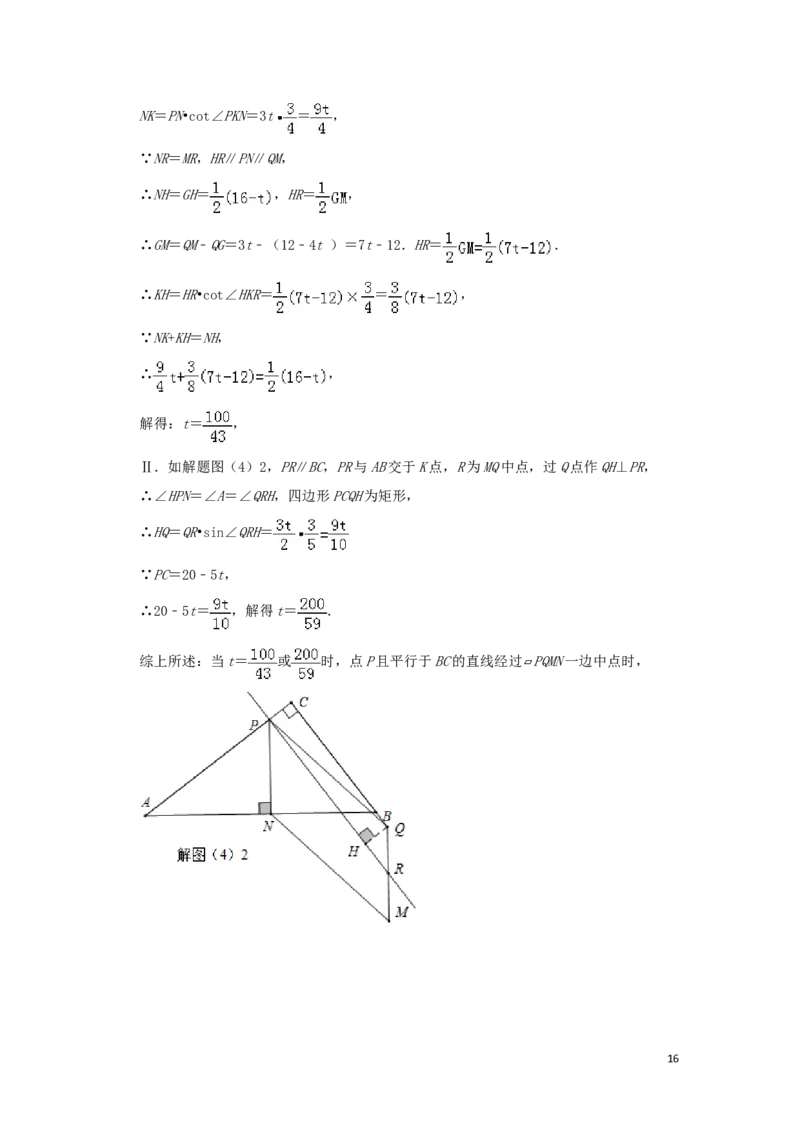
Ⅰ.如解题图(4)1,PR∥BC,PR与AB交于K点,R为MN中点,过R点作RH⊥AB,
∴∠PKN=∠HKR=∠B,
15NK=PN•cot∠PKN=3t = ,
∵NR=MR,HR∥PN∥QM,
∴NH=GH= ,HR= ,
∴GM=QM﹣QG=3t﹣(12﹣4t )=7t﹣12.HR= .
∴KH=HR•cot∠HKR= = ,
∵NK+KH=NH,
∴ ,
解得:t= ,
Ⅱ.如解题图(4)2,PR∥BC,PR与AB交于K点,R为MQ中点,过Q点作QH⊥PR,
∴∠HPN=∠A=∠QRH,四边形PCQH为矩形,
∴HQ=QR•sin∠QRH=
∵PC=20﹣5t,
∴20﹣5t= ,解得t= .
综上所述:当t= 或 时,点P且平行于BC的直线经过 PQMN一边中点时,
▱
1624.【解答】解:(1)当n=5时,
y= ,
①将P(4,b)代入y=﹣ x2+ x+ ,
∴b= ;
②当x≥5时,当x=5时有最大值为5;
当x<5时,当x= 时有最大值为 ;
∴函数的最大值为 ;
(2)将点(4,2)代入y=﹣x2+nx+n中,
17∴n= ,
∴ <n≤4时,图象与线段AB只有一个交点;
将点(2,2)代入y=﹣x2+nx+n中,
∴n=2,
将点(2,2)代入y=﹣ x2+ x+ 中,
∴n= ,
∴2≤n< 时图象与线段AB只有一个交点;
综上所述: <n≤4,2≤n< 时,图象与线段AB只有一个交点;
(3)当x=n时,y=﹣ n2+ n2+ = ,
>4,∴n>8;
当x= 时,y= + ,
+ ≤4,∴n≥ ,
当x=n时,y=﹣n2+n2+n=n,
n<4;
∴函数图象上有4个点到x轴的距离等于4时,n>8或n≤ <4.
1819