文档内容
江苏省盐城市二〇二〇年初中毕业与升学考试
数学试题
注意事项:
1.本次考试时间为120分钟,卷面总分为150分,考试形式为闭卷.
2.本试卷共6页,在检查是否有漏印、重印或错印后再开始答题.
3.所有试题必须作答在答题卡上规定的区域内,注意题号必须对应,否则不给分.
4.答题前,务必将姓名、准考证号用0.5毫米黑色签字笔填写在试卷及答题卡上.
一、选择题:本大题共8个小题,每小题3分,共24分.在每小题给出的四个选项中,只有
一项是符合题目要求的.
1.2020的相反数是( )
A. 2020 B. ﹣2020 C. D.
2.下列图形中,属于中心对称图形的是:( )
A. B.
C. D.
3.下列运算正确的是:( )
A. B. C. D.
4.实数 在数轴上表示的位置如图所示,则( )
A. B. C. D.
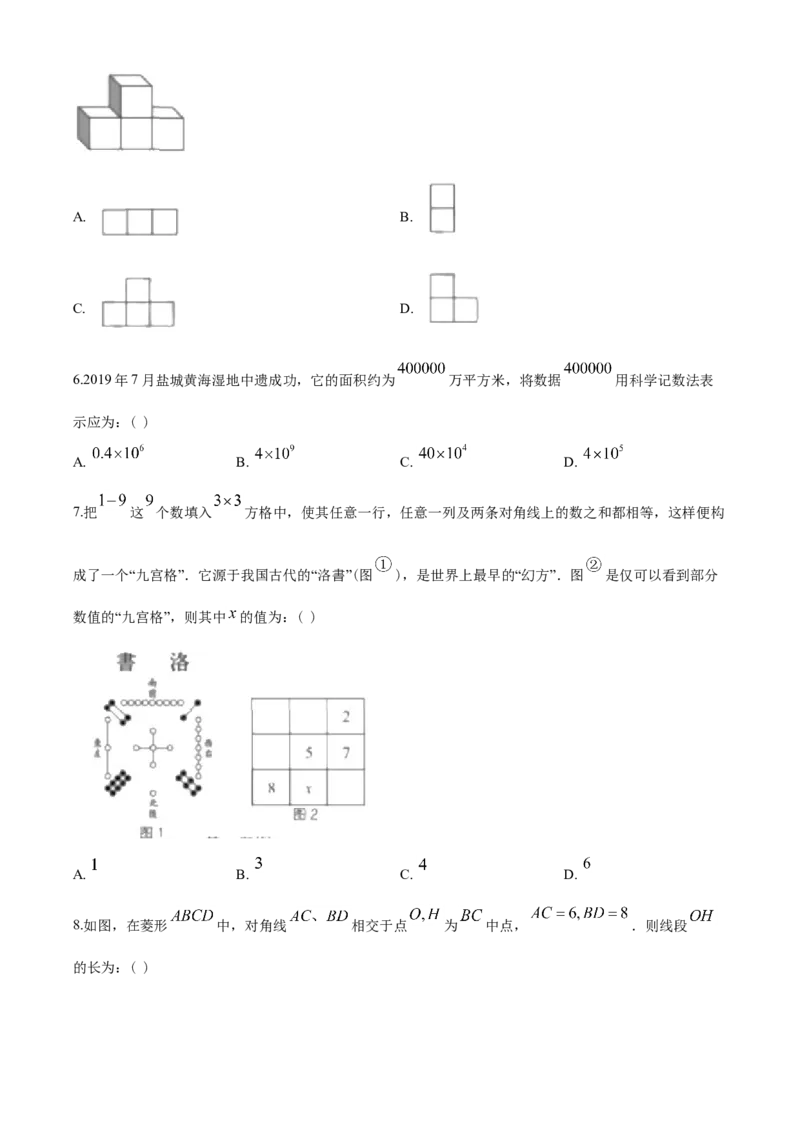
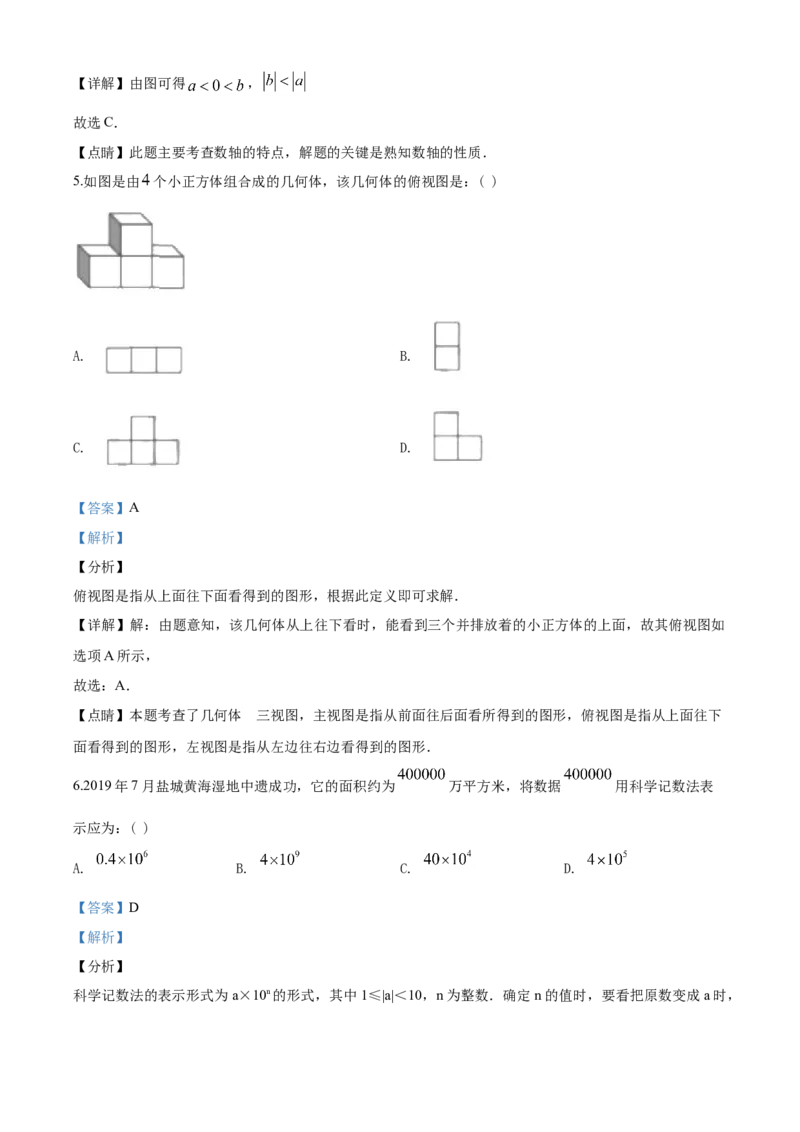
5.如图是由 个小正方体组合成的几何体,该几何体的俯视图是:( )A. B.
C. D.
6.2019年7月盐城黄海湿地中遗成功,它的面积约为 万平方米,将数据 用科学记数法表
示应为:( )
A. B. C. D.
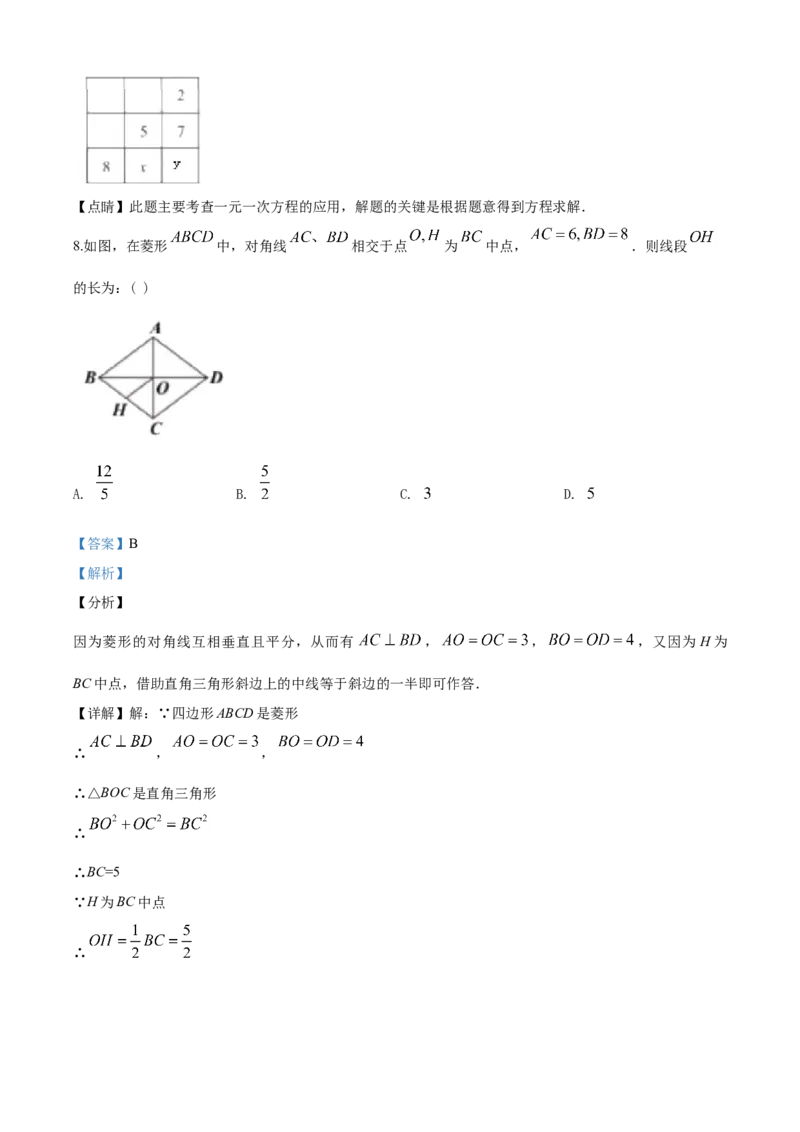
7.把 这 个数填入 方格中,使其任意一行,任意一列及两条对角线上的数之和都相等,这样便构
成了一个“九宫格”.它源于我国古代的“洛書”(图 ),是世界上最早的“幻方”.图 是仅可以看到部分
数值的“九宫格”,则其中 的值为:( )
A. B. C. D.
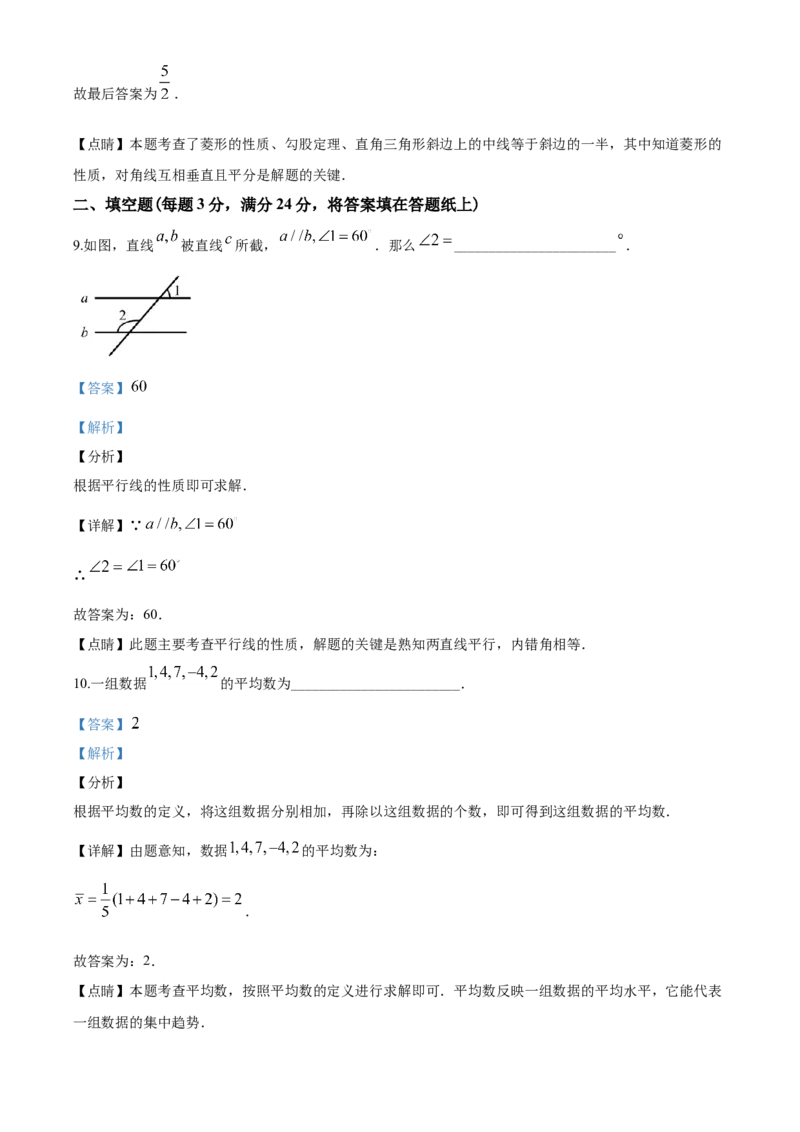
8.如图,在菱形 中,对角线 相交于点 为 中点, .则线段
的长为:( )A. B. C. D.
二、填空题(每题3分,满分24分,将答案填在答题纸上)
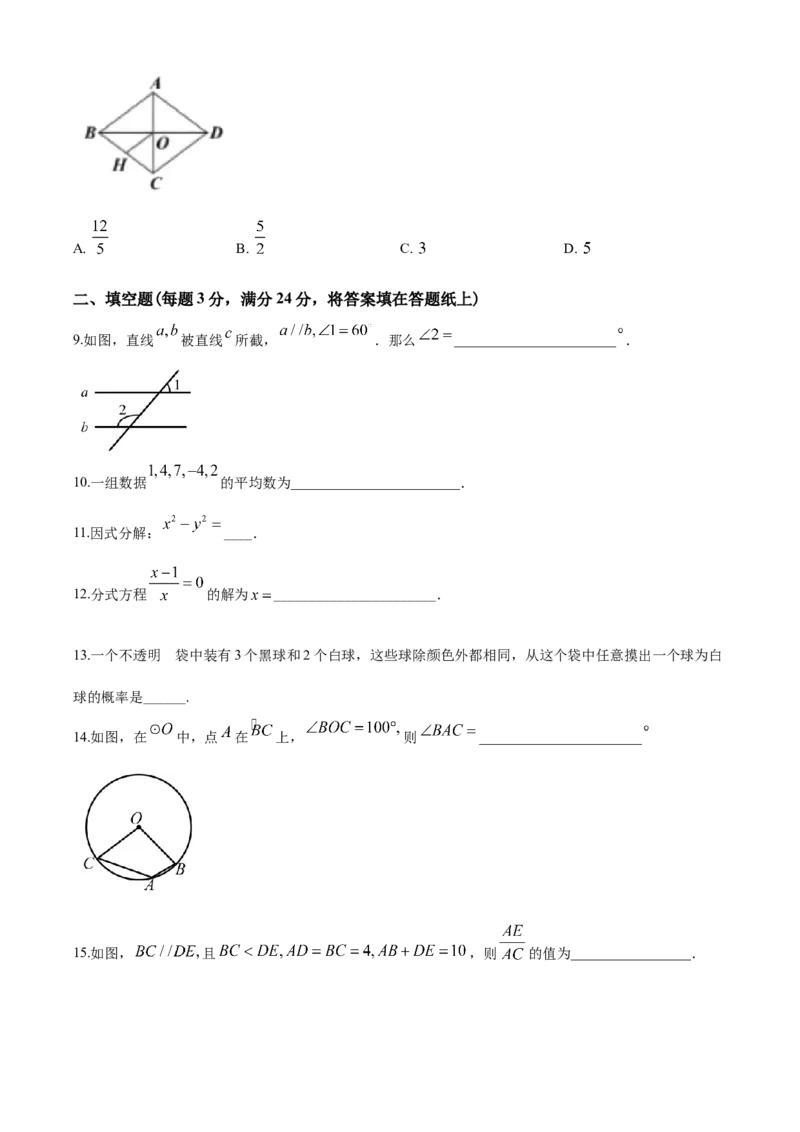
9.如图,直线 被直线 所截, .那么 _______________________ .
10.一组数据 的平均数为________________________.
11.因式分解: ____.
12.分式方程 的解为 _______________________.
的
13.一个不透明 袋中装有3个黑球和2个白球,这些球除颜色外都相同,从这个袋中任意摸出一个球为白
球的概率是______.
14.如图,在 中,点 在 上, 则 _______________________
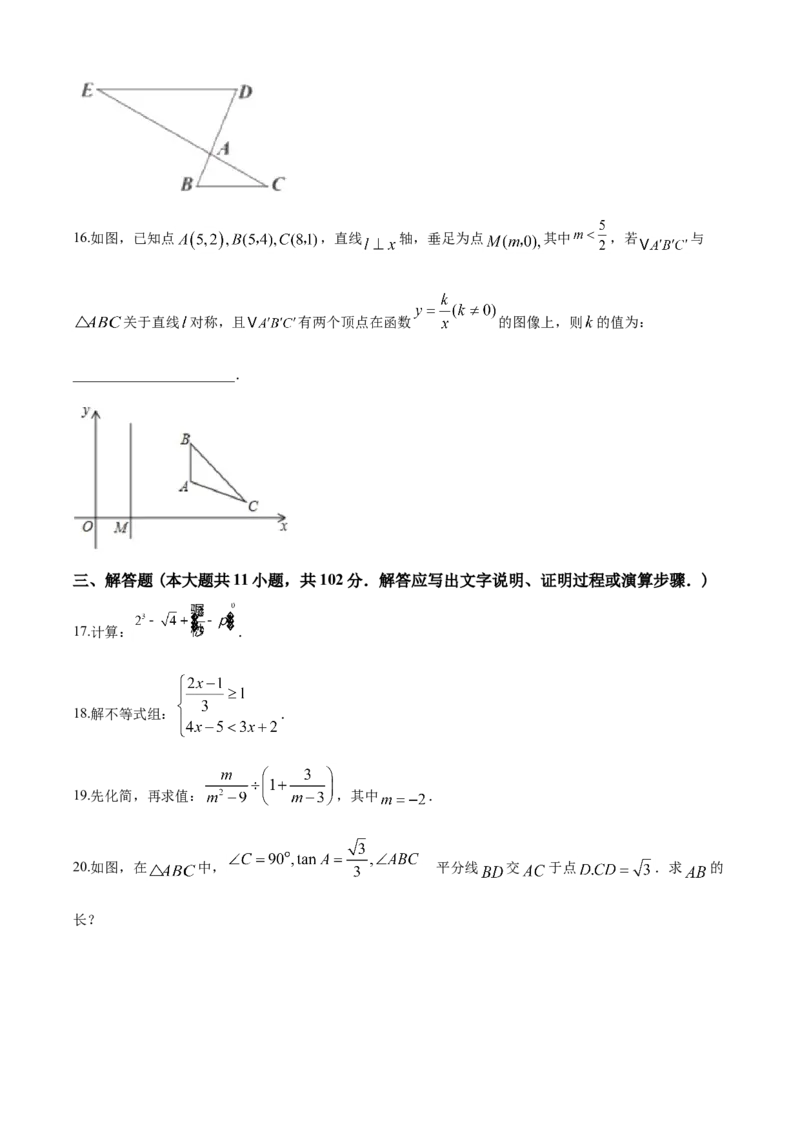
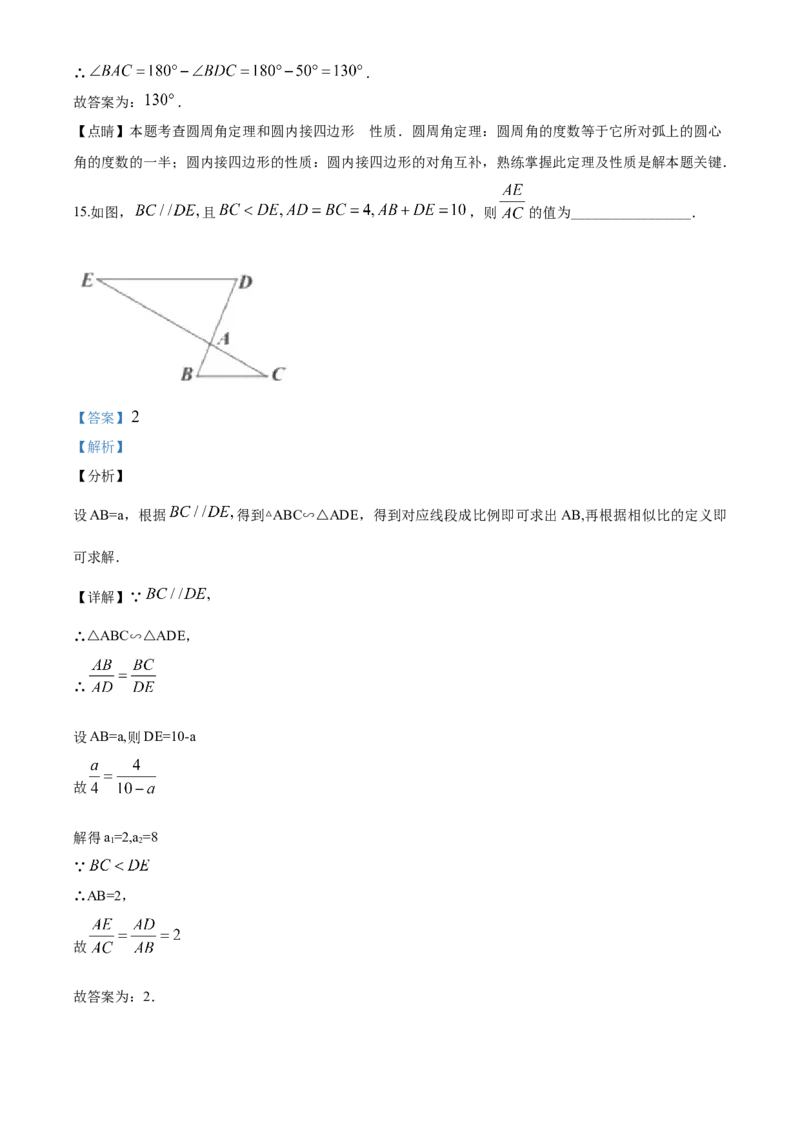
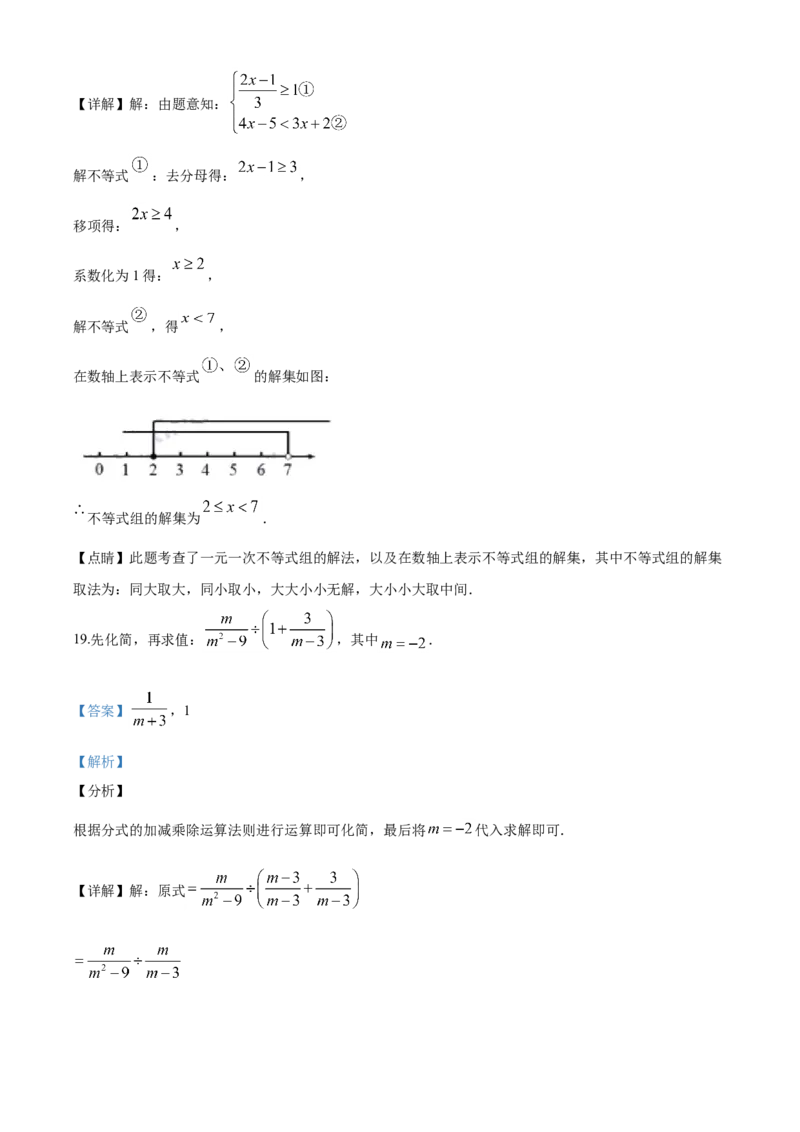
15.如图, 且 ,则 的值为_________________.16.如图,已知点 ,直线 轴,垂足为点 其中 ,若 与
关于直线 对称,且 有两个顶点在函数 的图像上,则 的值为:
_______________________.
三、解答题 (本大题共11小题,共102分.解答应写出文字说明、证明过程或演算步骤.)
17.计算: .
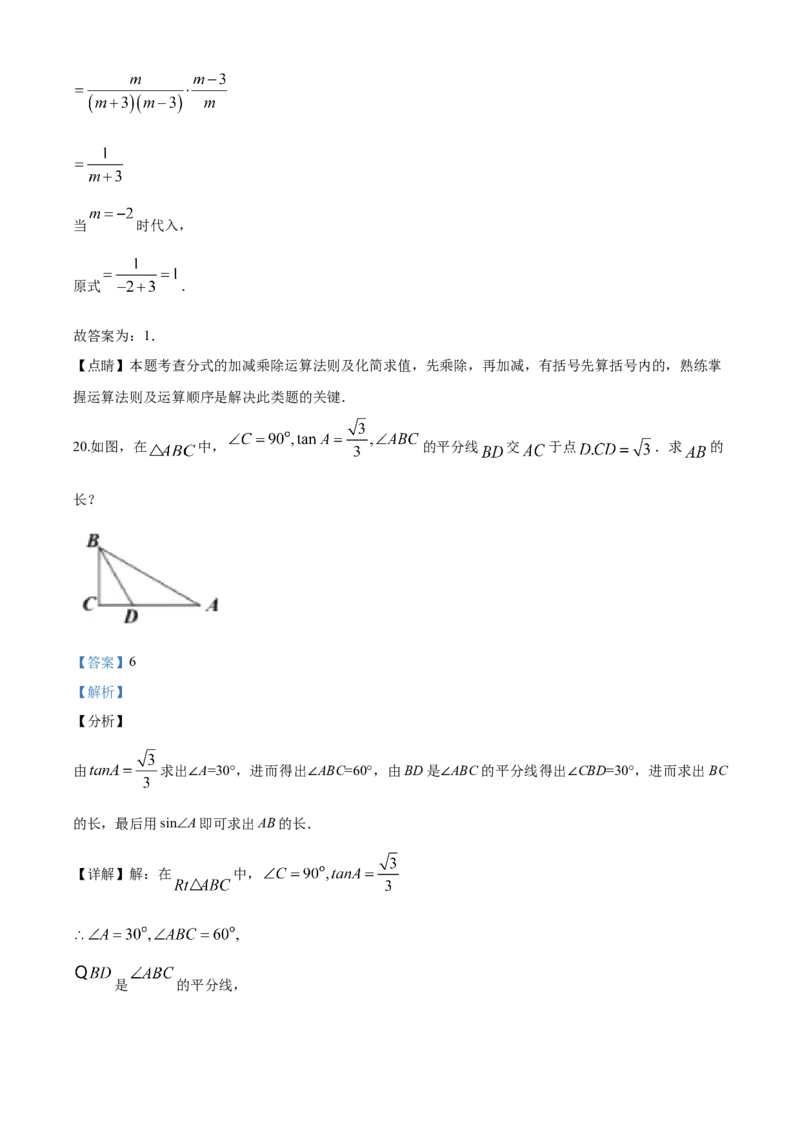
18.解不等式组: .
19.先化简,再求值: ,其中 .
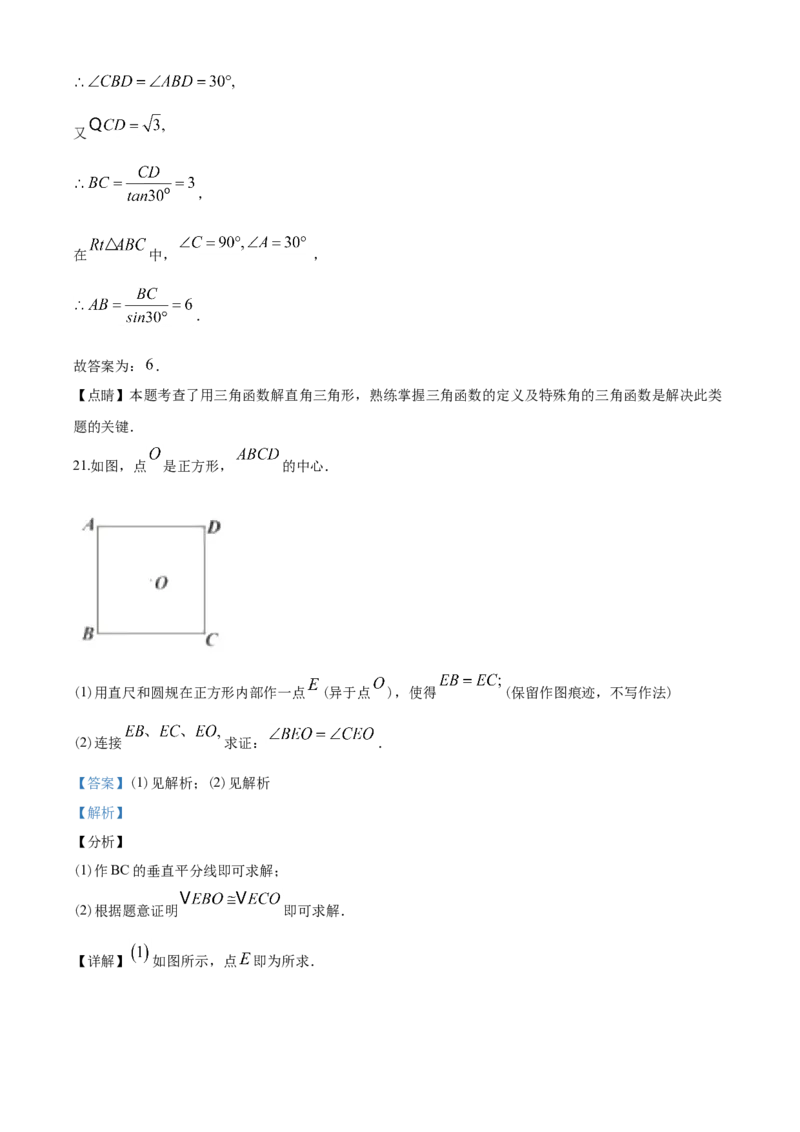
20.如图,在 中, 的平分线 交 于点 .求 的
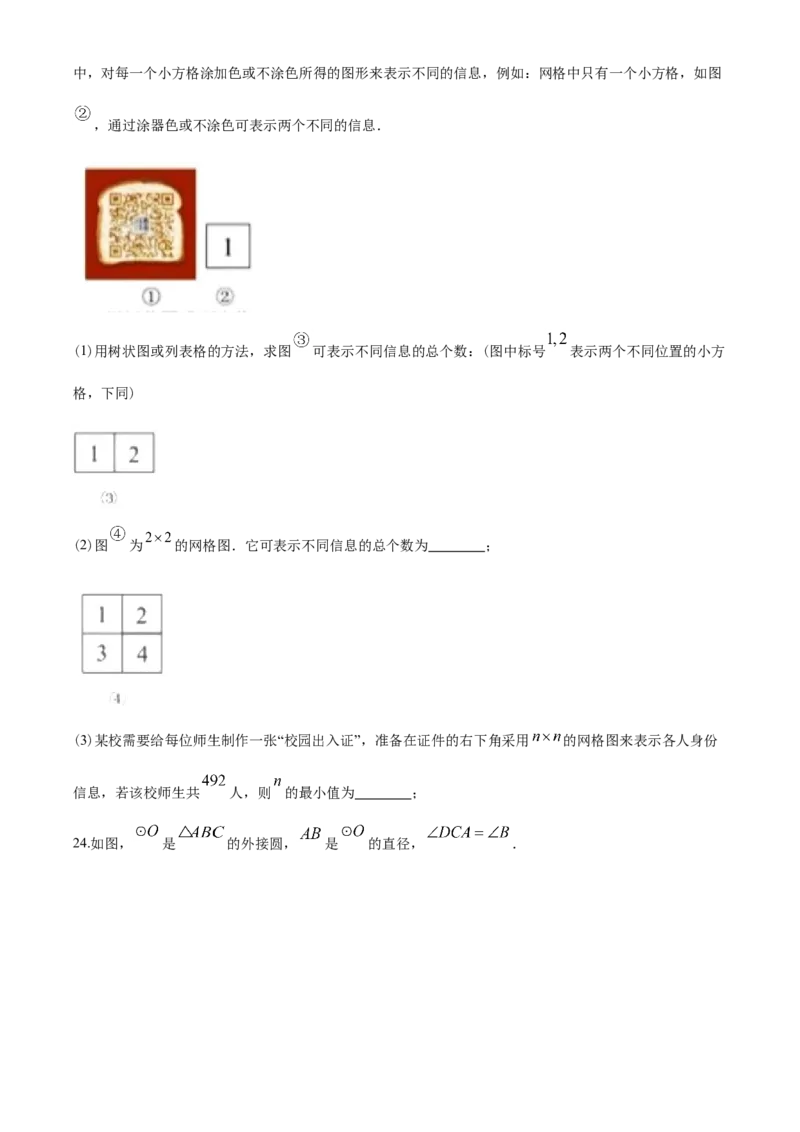
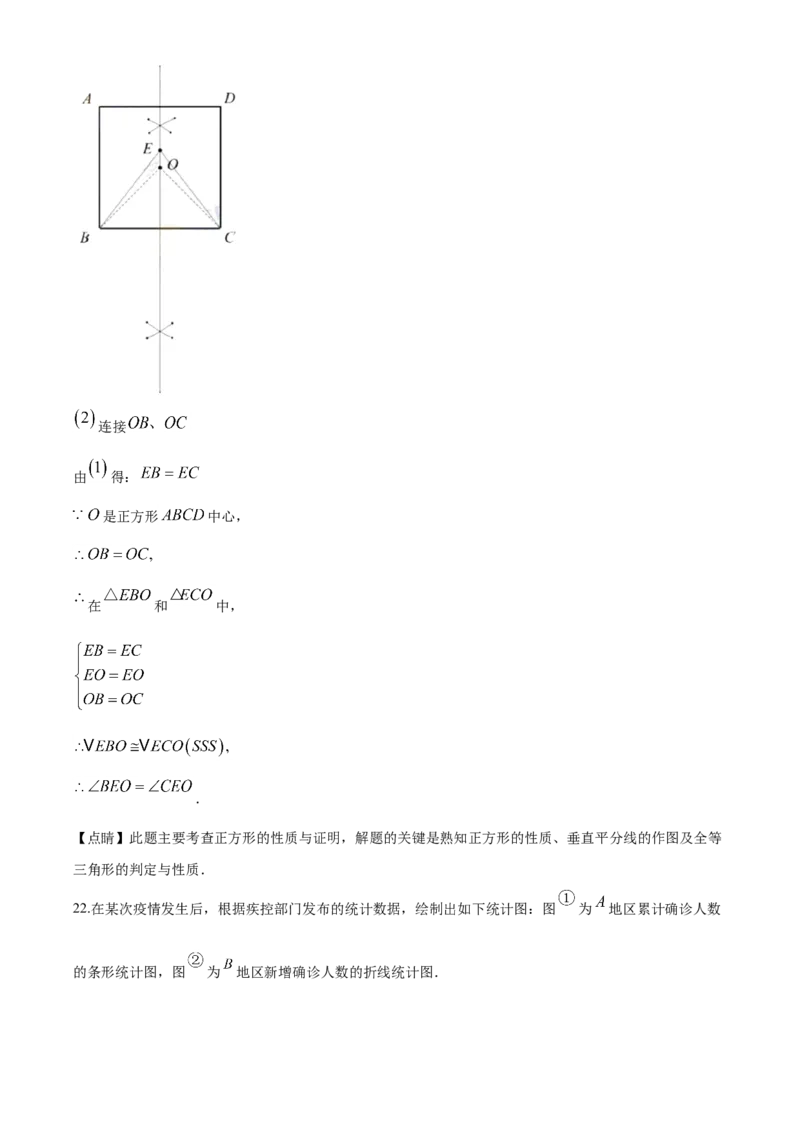
长?21.如图,点 是正方形, 的中心.
(1)用直尺和圆规在正方形内部作一点 (异于点 ),使得 (保留作图痕迹,不写作法)
(2)连接 求证: .
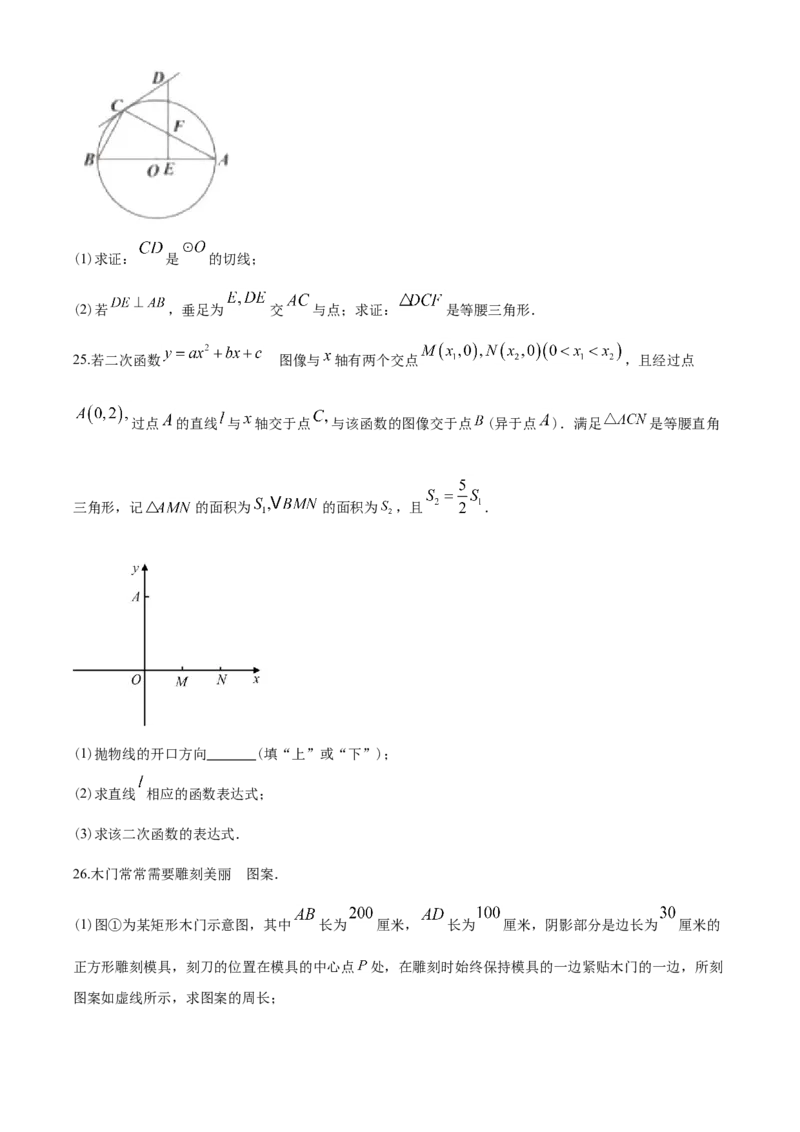
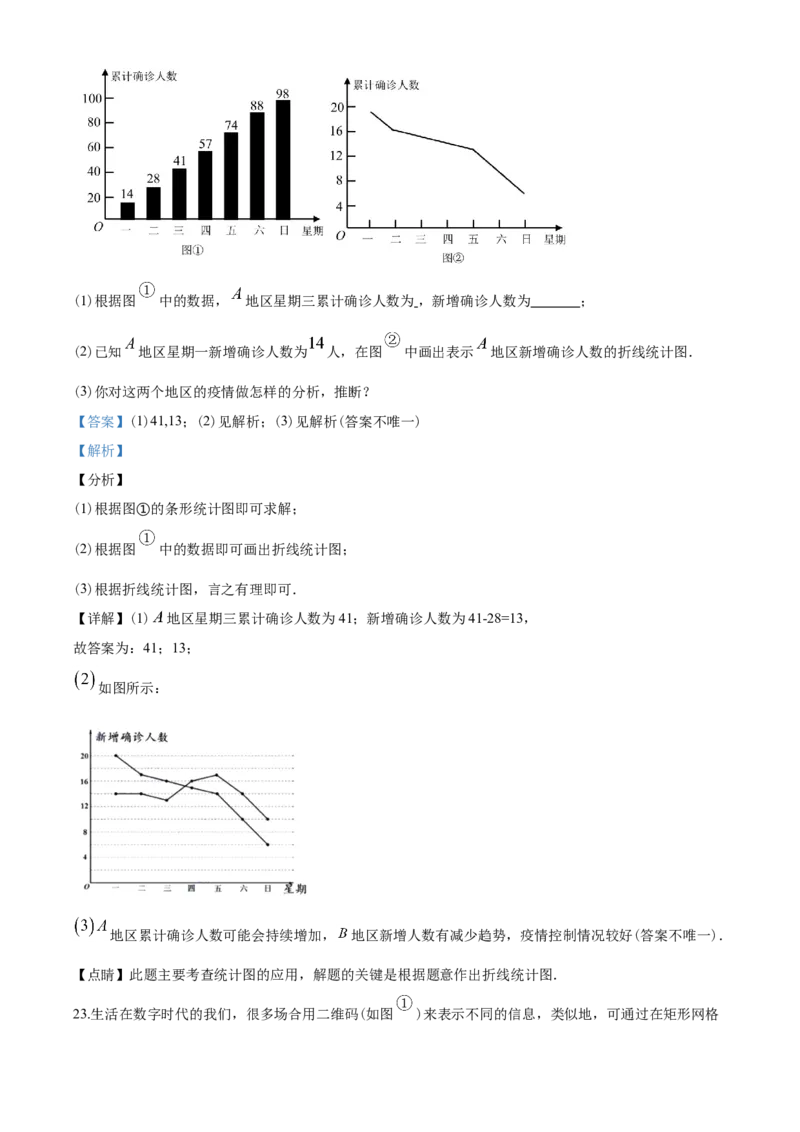
22.在某次疫情发生后,根据疾控部门发布的统计数据,绘制出如下统计图:图 为 地区累计确诊人数
的条形统计图,图 为 地区新增确诊人数的折线统计图.
(1)根据图 中的数据, 地区星期三累计确诊人数为 ,新增确诊人数为 ;
(2)已知 地区星期一新增确诊人数为 人,在图 中画出表示 地区新增确诊人数的折线统计图.
(3)你对这两个地区的疫情做怎样的分析,推断?
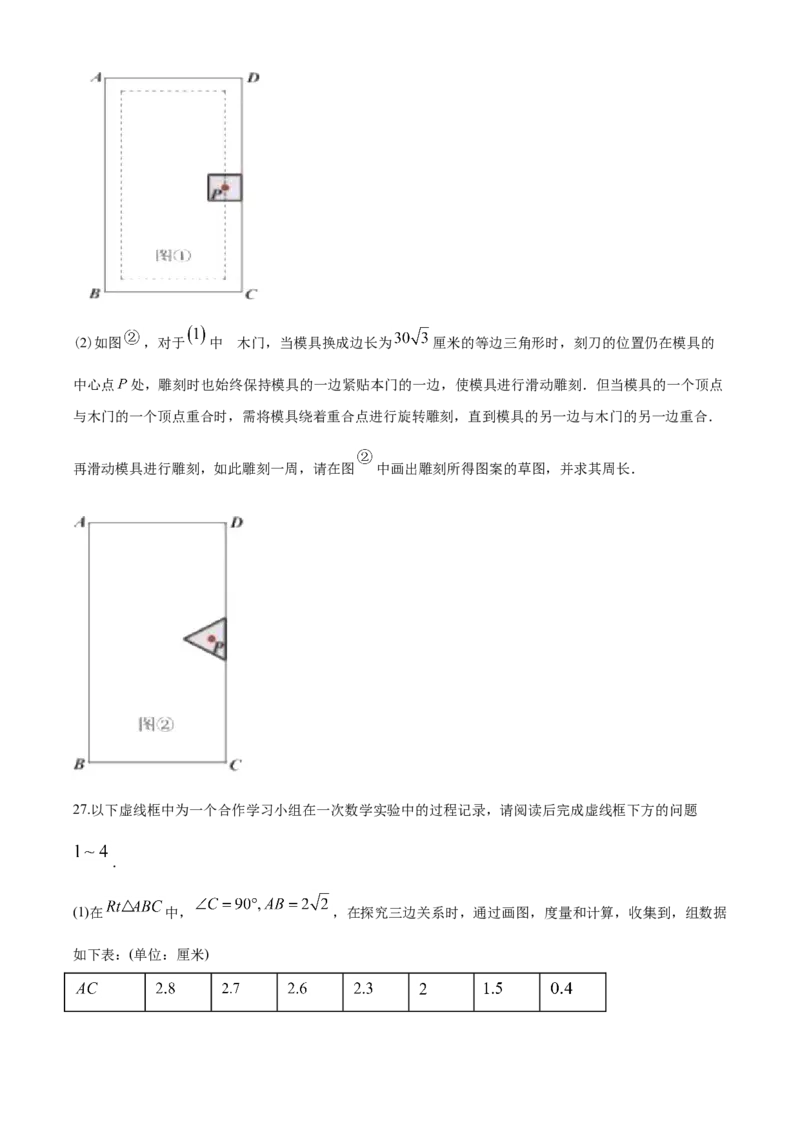
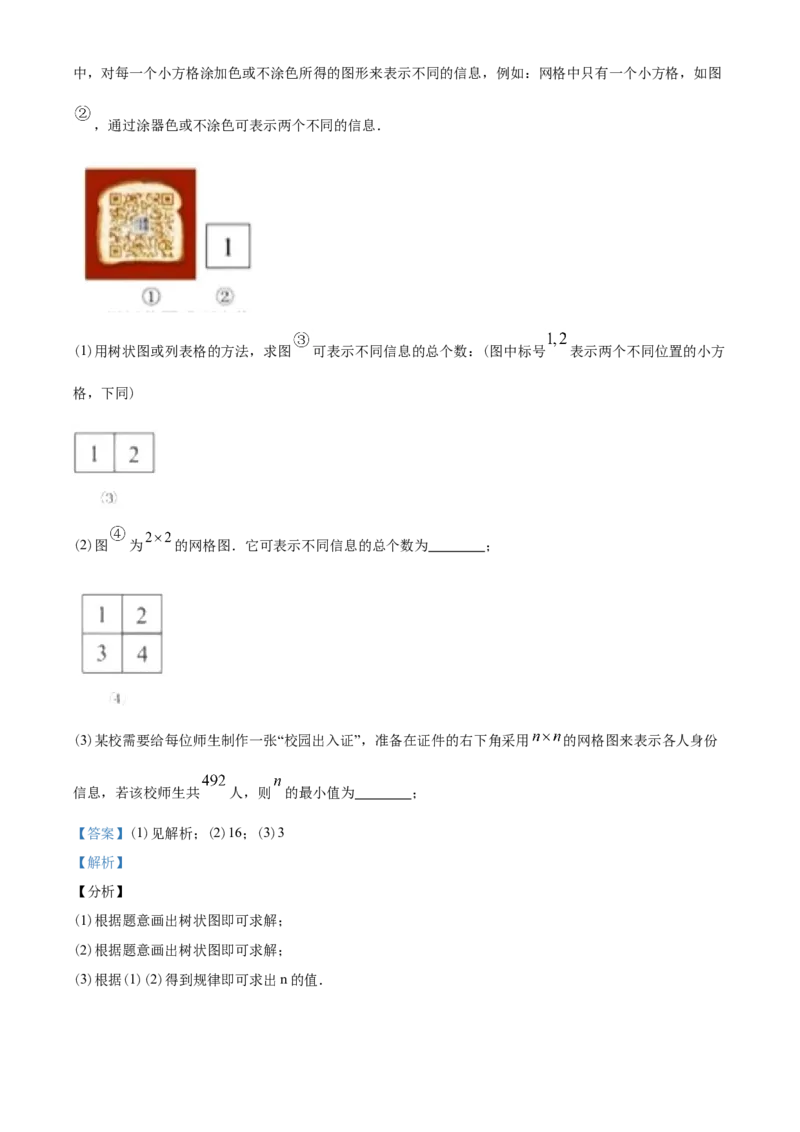
23.生活在数字时代的我们,很多场合用二维码(如图 )来表示不同的信息,类似地,可通过在矩形网格中,对每一个小方格涂加色或不涂色所得的图形来表示不同的信息,例如:网格中只有一个小方格,如图
,通过涂器色或不涂色可表示两个不同的信息.
(1)用树状图或列表格的方法,求图 可表示不同信息的总个数:(图中标号 表示两个不同位置的小方
格,下同)
(2)图 为 的网格图.它可表示不同信息的总个数为 ;
(3)某校需要给每位师生制作一张“校园出入证”,准备在证件的右下角采用 的网格图来表示各人身份
信息,若该校师生共 人,则 的最小值为 ;
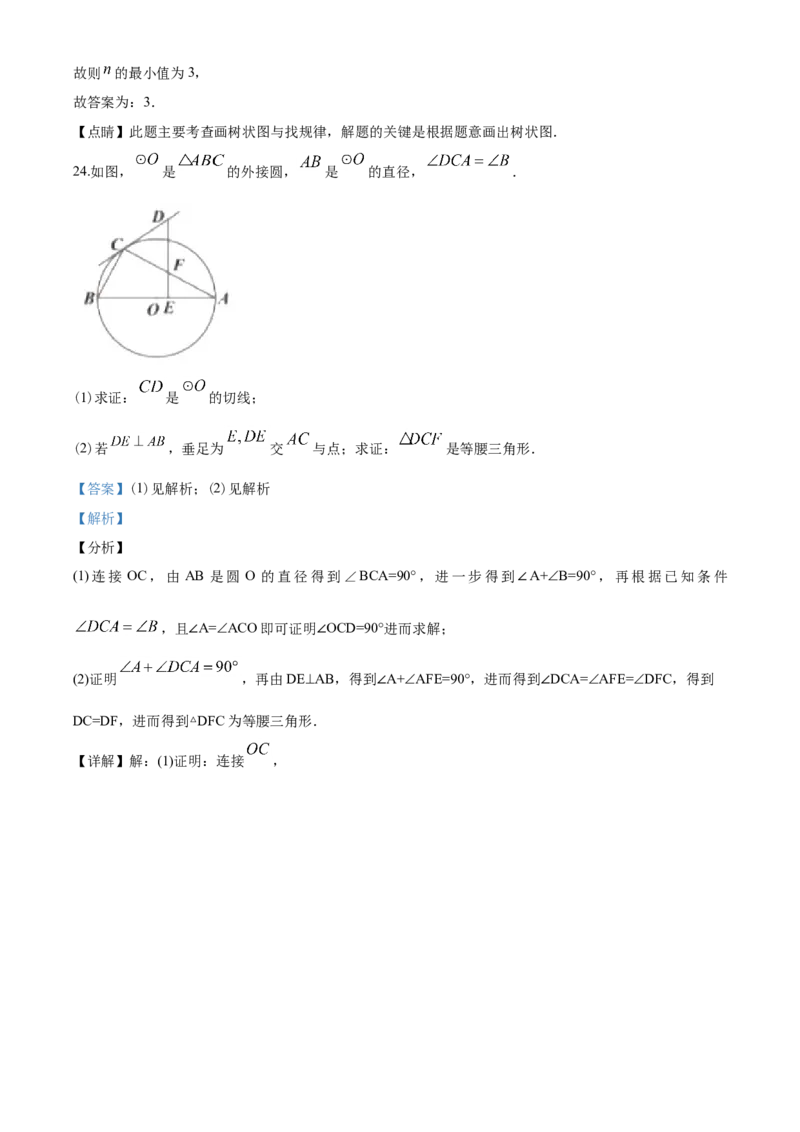
24.如图, 是 的外接圆, 是 的直径, .(1)求证: 是 的切线;
(2)若 ,垂足为 交 与点;求证: 是等腰三角形.
的
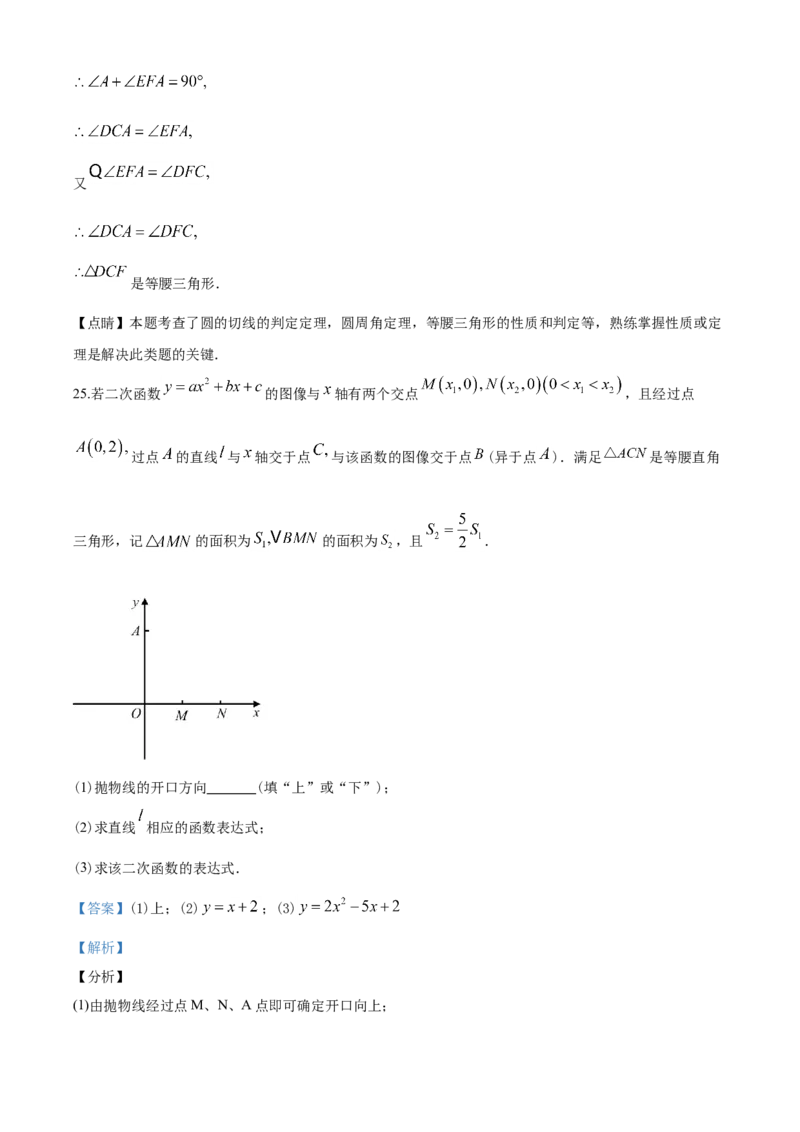
25.若二次函数 图像与 轴有两个交点 ,且经过点
过点 的直线 与 轴交于点 与该函数的图像交于点 (异于点 ).满足 是等腰直角
三角形,记 的面积为 的面积为 ,且 .
(1)抛物线的开口方向 (填“上”或“下”);
(2)求直线 相应的函数表达式;
(3)求该二次函数的表达式.
的
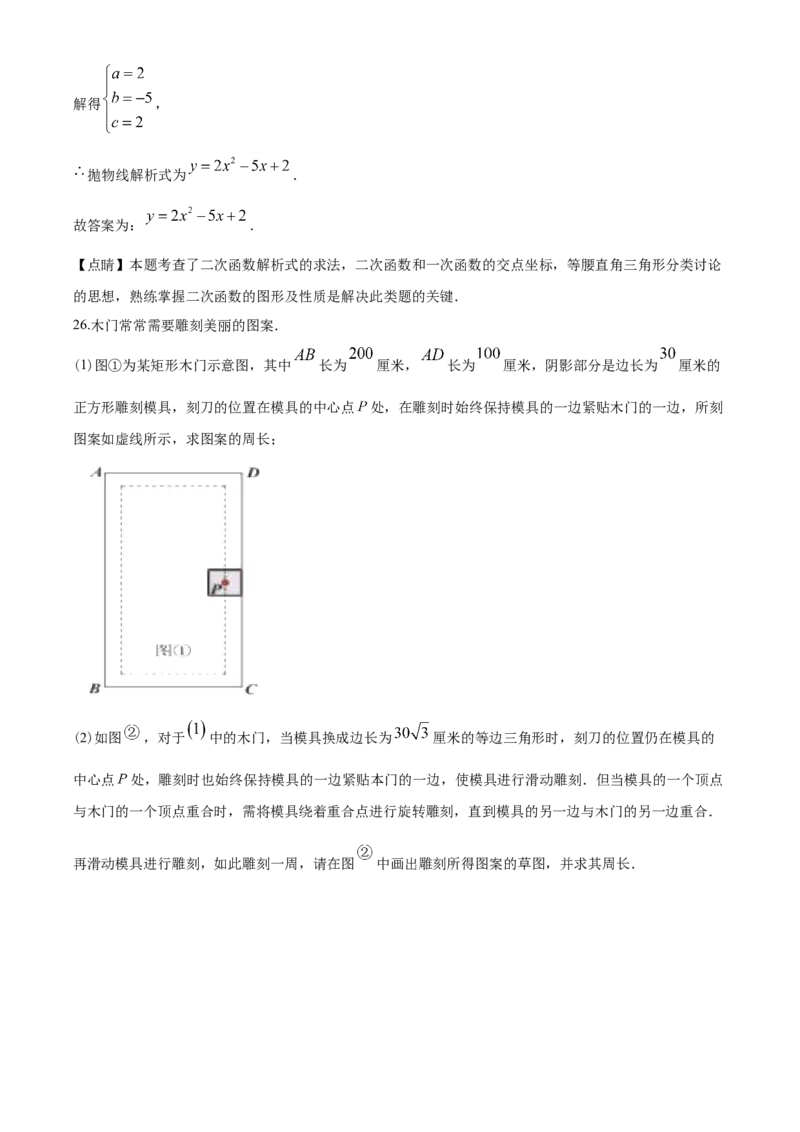
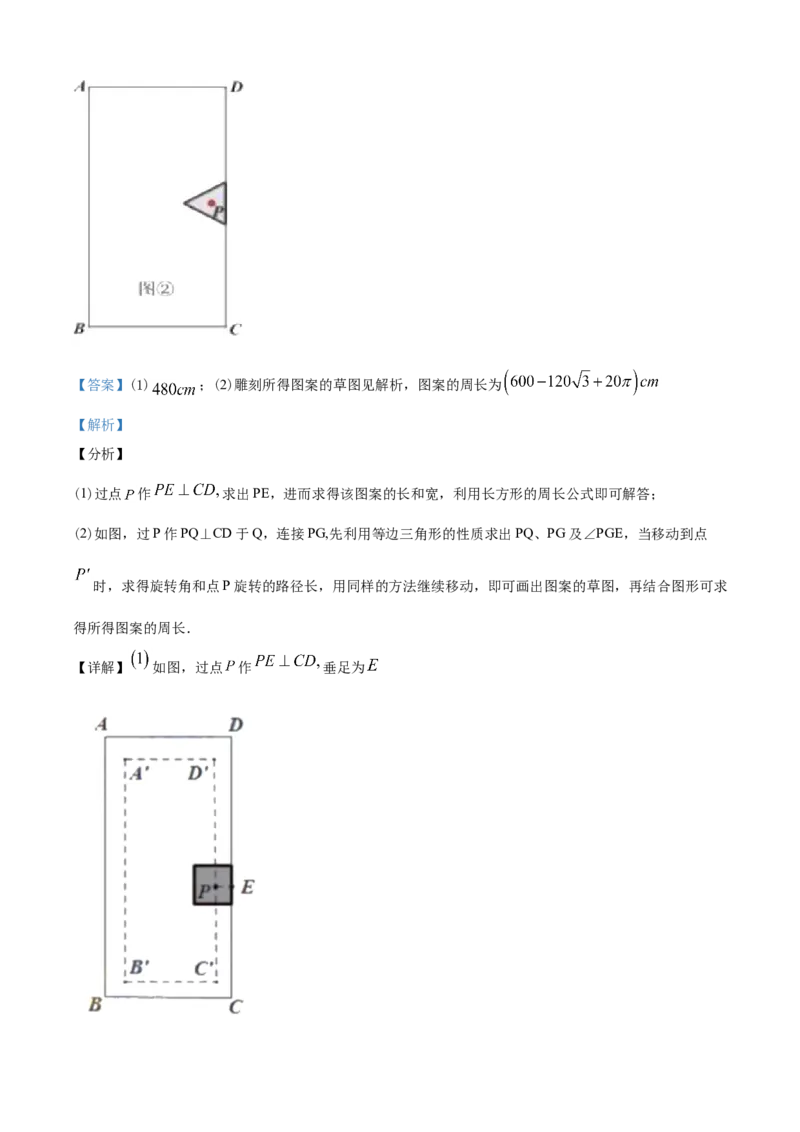
26.木门常常需要雕刻美丽 图案.
(1)图①为某矩形木门示意图,其中 长为 厘米, 长为 厘米,阴影部分是边长为 厘米的
正方形雕刻模具,刻刀的位置在模具的中心点 处,在雕刻时始终保持模具的一边紧贴木门的一边,所刻
图案如虚线所示,求图案的周长;(2)如图 ,对于 中 的木门,当模具换成边长为 厘米的等边三角形时,刻刀的位置仍在模具的
中心点 处,雕刻时也始终保持模具的一边紧贴本门的一边,使模具进行滑动雕刻.但当模具的一个顶点
与木门的一个顶点重合时,需将模具绕着重合点进行旋转雕刻,直到模具的另一边与木门的另一边重合.
再滑动模具进行雕刻,如此雕刻一周,请在图 中画出雕刻所得图案的草图,并求其周长.
27.以下虚线框中为一个合作学习小组在一次数学实验中的过程记录,请阅读后完成虚线框下方的问题
.
(1)在 中, ,在探究三边关系时,通过画图,度量和计算,收集到,组数据
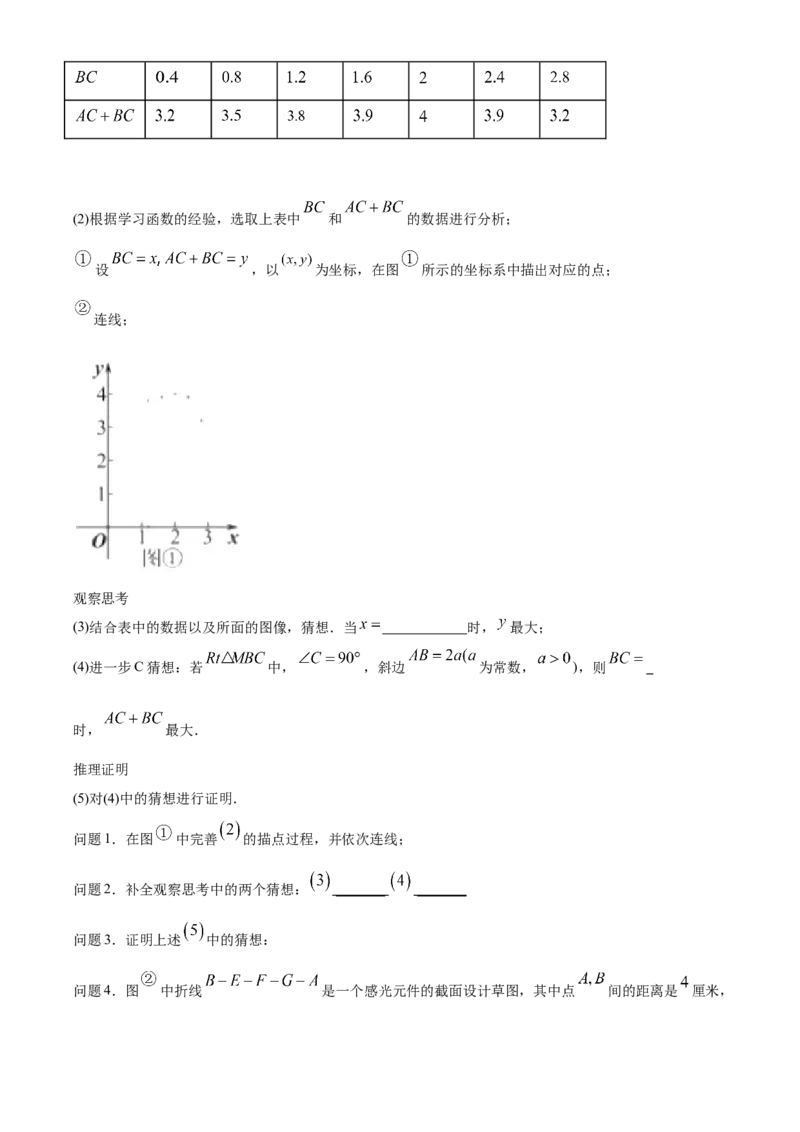
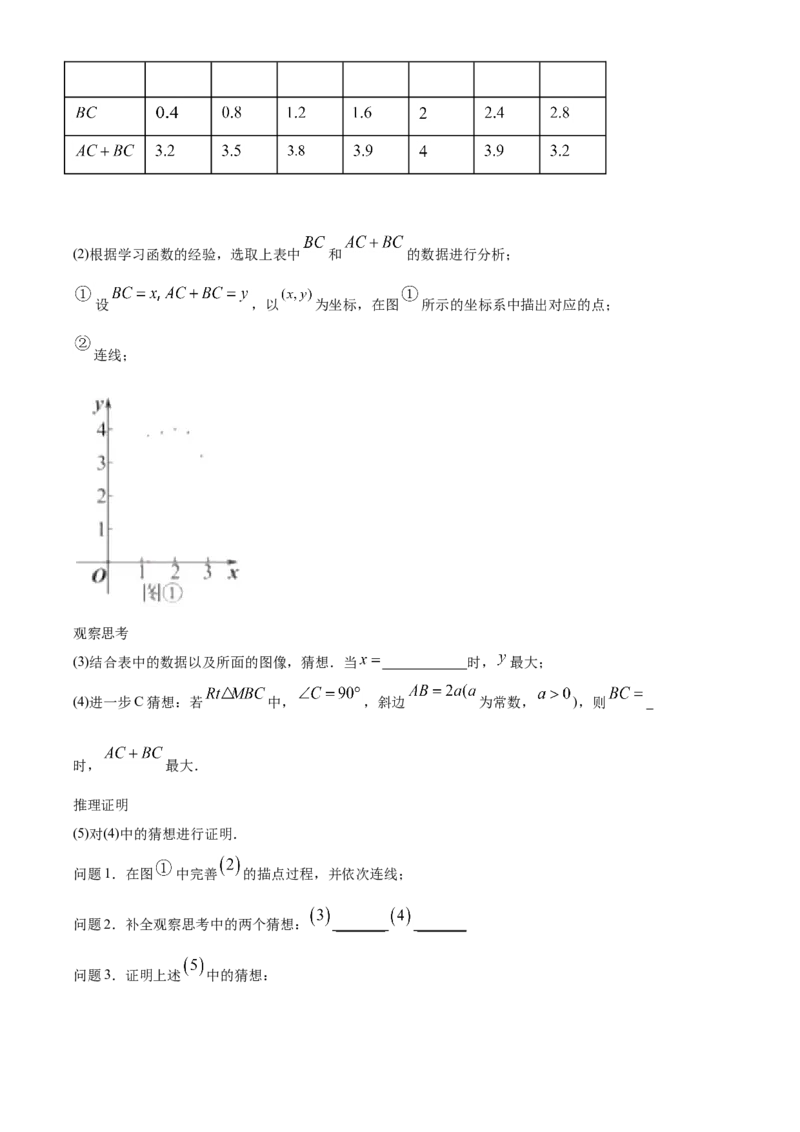
如下表:(单位:厘米)(2)根据学习函数的经验,选取上表中 和 的数据进行分析;
设 ,以 为坐标,在图 所示的坐标系中描出对应的点;
连线;
观察思考
(3)结合表中的数据以及所面的图像,猜想.当 时, 最大;
(4)进一步C猜想:若 中, ,斜边 为常数, ),则
时, 最大.
推理证明
(5)对(4)中的猜想进行证明.
问题1.在图 中完善 的描点过程,并依次连线;
问题2.补全观察思考中的两个猜想: _______ _______
问题3.证明上述 中的猜想:
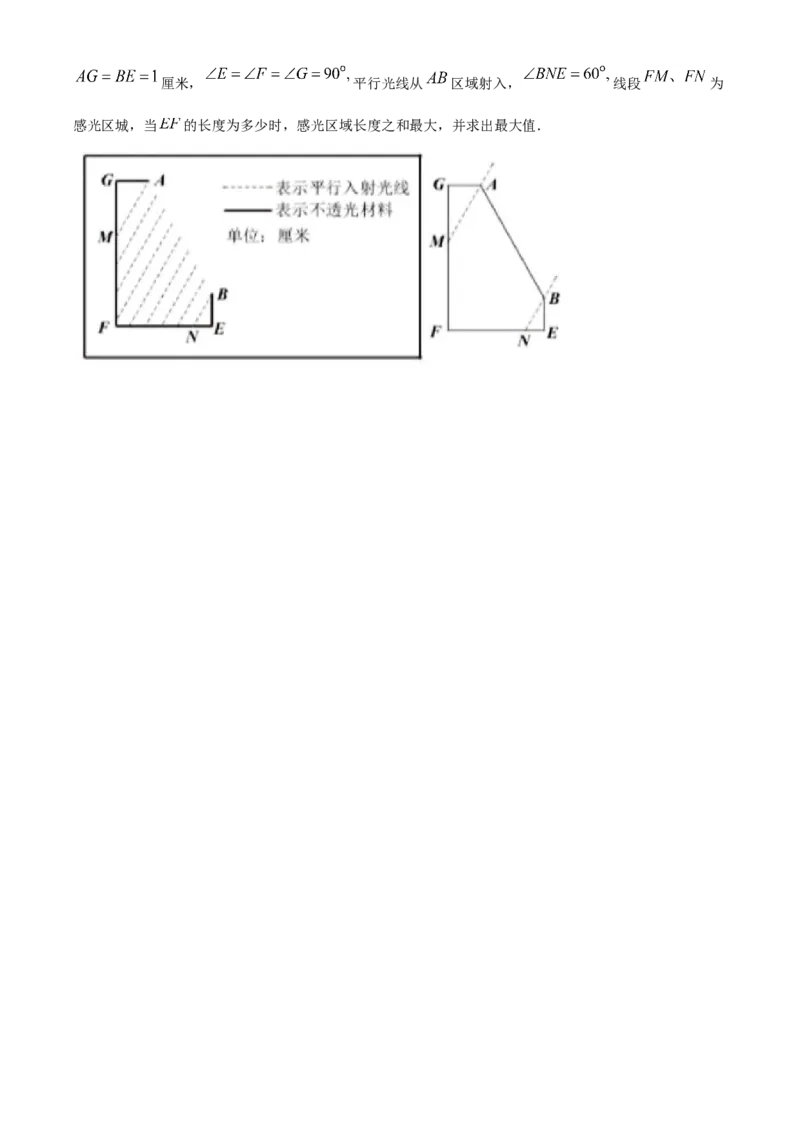
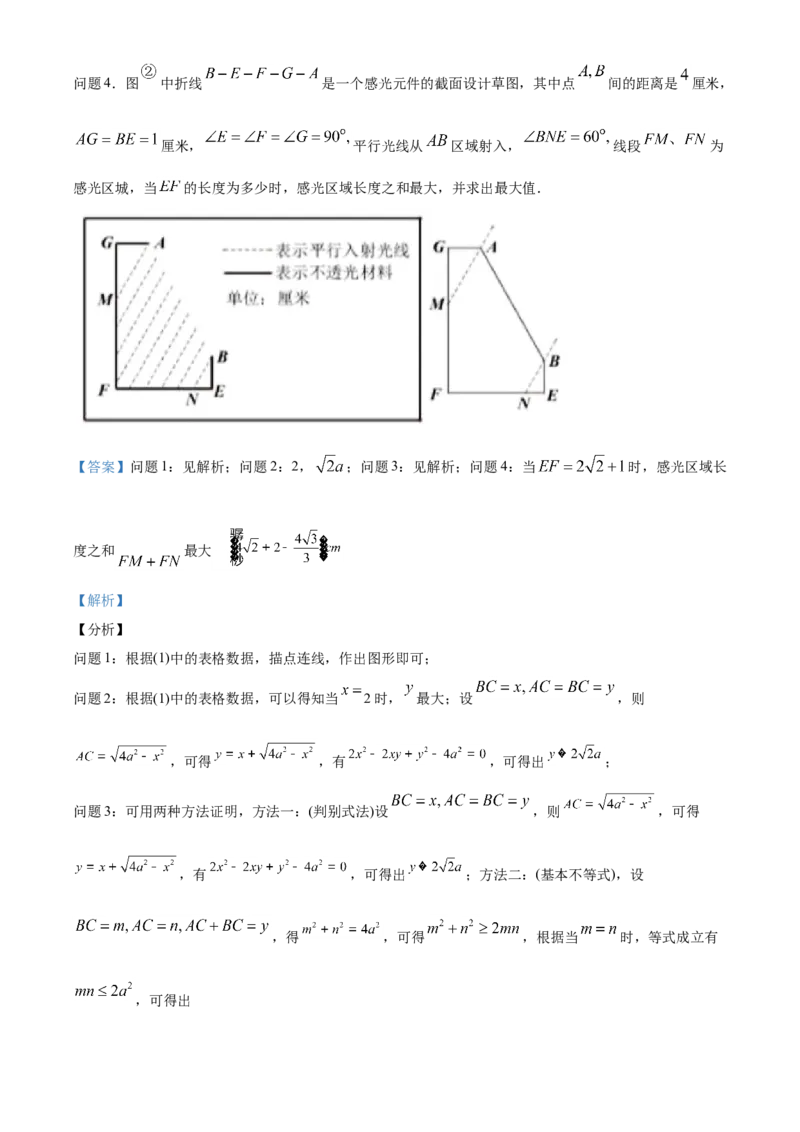
问题4.图 中折线 是一个感光元件的截面设计草图,其中点 间的距离是 厘米,厘米, 平行光线从 区域射入, 线段 为
感光区城,当 的长度为多少时,感光区域长度之和最大,并求出最大值.江苏省盐城市二〇二〇年初中毕业与升学考试
数学试题
注意事项:
1.本次考试时间为120分钟,卷面总分为150分,考试形式为闭卷.
2.本试卷共6页,在检查是否有漏印、重印或错印后再开始答题.
3.所有试题必须作答在答题卡上规定的区域内,注意题号必须对应,否则不给分.
4.答题前,务必将姓名、准考证号用0.5毫米黑色签字笔填写在试卷及答题卡上.
一、选择题:本大题共8个小题,每小题3分,共24分.在每小题给出的四个选项中,只有
一项是符合题目要求的.
1.2020的相反数是( )
A. 2020 B. ﹣2020 C. D.
【答案】B
【解析】
【分析】
直接利用相反数的定义得出答案.
【详解】解:2020的相反数是:﹣2020.
故选:B.
【点睛】此题主要考查了相反数,正确把握相反数的定义是解题关键.
2.下列图形中,属于中心对称图形的是:( )
A. B.
C. D.
【答案】B
【解析】
【分析】根据中心对称图形的概念即图形旋转180°后与原图重合即可求解.
【详解】解:解:A、不是中心对称图形,故此选项错误;
B、是中心对称图形,故此选项正确;
C、不是中心对称图形,故此选项错误;
D、不是中心对称图形,故此选项错误,
故选:B.
【点睛】本题主要考查了中心对称图形的概念,中心对称图形关键是要寻找对称中心,图形旋转180°后
与原图重合.
3.下列运算正确的是:( )
A. B. C. D.
【答案】C
【解析】
【分析】
根据整式的加减与幂的运算法则即可判断.
【详解】A. ,故错误;
B. ,故错误;
C. ,正确;
D. ,故错误;
故选C.
【点睛】此题主要考查整式与幂的运算,解题的关键是熟知其运算法则.
4.实数 在数轴上表示的位置如图所示,则( )
A. B. C. D.
【答案】C
【解析】
【分析】
根据数轴的特点即可求解.【详解】由图可得 ,
故选C.
【点睛】此题主要考查数轴的特点,解题的关键是熟知数轴的性质.
5.如图是由 个小正方体组合成的几何体,该几何体的俯视图是:( )
A. B.
C. D.
【答案】A
【解析】
【分析】
俯视图是指从上面往下面看得到的图形,根据此定义即可求解.
【详解】解:由题意知,该几何体从上往下看时,能看到三个并排放着的小正方体的上面,故其俯视图如
选项A所示,
故选:A.
【点睛】本题考查了几何体 的三视图,主视图是指从前面往后面看所得到的图形,俯视图是指从上面往下
面看得到的图形,左视图是指从左边往右边看得到的图形.
6.2019年7月盐城黄海湿地中遗成功,它的面积约为 万平方米,将数据 用科学记数法表
示应为:( )
A. B. C. D.
【答案】D
【解析】
【分析】
科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值大于等于1时,n是正数;当原
数的绝对值小于1时,n是负数.
【详解】解:由题意可知,将 用科学记数法表示为: ,
故选:D.
【点睛】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为
整数,表示时关键要正确确定a的值以及n的值.
7.把 这 个数填入 方格中,使其任意一行,任意一列及两条对角线上的数之和都相等,这样便构
成了一个“九宫格”.它源于我国古代的“洛書”(图 ),是世界上最早的“幻方”.图 是仅可以看到部分
数值的“九宫格”,则其中 的值为:( )
A. B. C. D.
【答案】A
【解析】
【分析】
根据题意求出“九宫格”中的y,再求出x即可求解.
【详解】如图,依题意可得2+5+8=2+7+y
解得y=6
∴8+x+6=2+5+8
解得x=1
故选A.【点睛】此题主要考查一元一次方程的应用,解题的关键是根据题意得到方程求解.
8.如图,在菱形 中,对角线 相交于点 为 中点, .则线段
的长为:( )
A. B. C. D.
【答案】B
【解析】
【分析】
因为菱形的对角线互相垂直且平分,从而有 , , ,又因为H为
BC中点,借助直角三角形斜边上的中线等于斜边的一半即可作答.
【详解】解:∵四边形ABCD是菱形
∴ , ,
∴△BOC是直角三角形
∴
∴BC=5
∵H为BC中点
∴故最后答案为 .
【点睛】本题考查了菱形的性质、勾股定理、直角三角形斜边上的中线等于斜边的一半,其中知道菱形的
性质,对角线互相垂直且平分是解题的关键.
二、填空题(每题3分,满分24分,将答案填在答题纸上)
9.如图,直线 被直线 所截, .那么 _______________________ .
【答案】
【解析】
【分析】
根据平行线的性质即可求解.
【详解】∵
∴
故答案为:60.
【点睛】此题主要考查平行线的性质,解题的关键是熟知两直线平行,内错角相等.
10.一组数据 的平均数为________________________.
【答案】
【解析】
【分析】
根据平均数的定义,将这组数据分别相加,再除以这组数据的个数,即可得到这组数据的平均数.
【详解】由题意知,数据 的平均数为:
.
故答案为:2.
【点睛】本题考查平均数,按照平均数的定义进行求解即可.平均数反映一组数据的平均水平,它能代表
一组数据的集中趋势.11.因式分解: ____.
【答案】 ;
【解析】
试题分析:直接利用平方差公式分解:x2-y2=(x+y)(x-y).
故答案为(x+y)(x-y).
12.分式方程 的解为 _______________________.
【答案】
【解析】
【分析】
方程两边同时乘 化成整式方程,进而求出 的值,最后再检验即可.
【详解】解:方程两边同时乘 得:
,
解得: ,
检验,当 时分母不为0,
故原分式方程的解为 .
故答案为:1.
【点睛】本题考查分式方程的解法,先方程两边同时乘以最简公分母化成整式方程,然后求解,最后要记
得检验.
的
13.一个不透明 袋中装有3个黑球和2个白球,这些球除颜色外都相同,从这个袋中任意摸出一个球为白
球的概率是______.
【答案】 .
【解析】
【分析】
根据概率的求法,找准两点:①全部的情况数;②符合条件的情况数;二者的比值就是其发生的概率.
【详解】解:根据题意可得:不透明的袋子里共有将5个球,其中2个白球,∴任意摸出一个球为白球的概率是: ,
故答案为 .
【点睛】本题考查了概率公式:随机事件A的概率P(A)=事件A可能出现的结果数除以所有可能出现的结
果数.
14.如图,在 中,点 在 上, 则 _______________________
【答案】
【解析】
【分析】
画出 的圆周角 交 于点 ,构造出 的内接四边形;根据圆周角定理求出 的度
数,再根据圆内接四边形的性质,即可得出 的度数.
【详解】如图,画出 的圆周角 交 于点 ,则四边形 为 的内接四边形,
∵圆周角 的度数等于它所对弧上的圆心角的度数的一半,
∴ ,
∵四边形 为 的内接四边形,
∴ ,∴ .
故答案为: .
【点睛】本题考查圆周角定理和圆内接四边形 的性质.圆周角定理:圆周角的度数等于它所对弧上的圆心
角的度数的一半;圆内接四边形的性质:圆内接四边形的对角互补,熟练掌握此定理及性质是解本题关键.
15.如图, 且 ,则 的值为_________________.
【答案】
【解析】
【分析】
设AB=a,根据 得到△ABC∽△ADE,得到对应线段成比例即可求出AB,再根据相似比的定义即
可求解.
【详解】∵
∴△ABC∽△ADE,
∴
设AB=a,则DE=10-a
故
解得a=2,a =8
1 2
∵
∴AB=2,
故
故答案为:2.【点睛】此题主要考查相似三角形的性质与判定,解题的关键是熟知得到对应线段成比例.
16.如图,已知点 ,直线 轴,垂足为点 其中 ,若 与
关于直线 对称,且 有两个顶点在函数 的图像上,则 的值为:
_______________________.
【答案】 或
【解析】
【分析】
因为 与 关于直线l对称,且直线 轴,从而有互为对称点纵坐标相同,横坐标之和为
2m,利用等量关系计算出m的值,又由于 有两个顶点在函数 ,从而进行分情况讨论
是哪两个点在函数上,求出k的值.
【详解】解:∵ 与 关于直线l对称,直线 轴,垂足为点 ,
∴ , ,
∵ 有两个顶点在函数
(1)设 , 在直线 上,
代入有 , 不符合 故不成立;(2)设 , 在直线 上,
有 , , , ,代入方程后k=-6;
(3)设 , 在直线 上,
有 , , , ,代入方程后有k=-4;
综上所述,k=-6或k=-4;
故答案为:-6或-4.
【点睛】本题考查轴对称图形的坐标关系以及反比例函数解析式,其中明确轴对称图形纵坐标相等,横坐
标之和为对称轴横坐标的2倍是解题的关键.
三、解答题 (本大题共11小题,共102分.解答应写出文字说明、证明过程或演算步骤.)
17.计算: .
【答案】7
【解析】
【分析】
根据乘方,二次根式和零指数幂的运算法则化简,然后再计算即可.
【详解】解:原式
.
【点睛】本题主要考查了乘方,二次根式和零指数幂的运算法则,熟练掌握运算法则是解题的关键.
18.解不等式组: .
【答案】
【解析】
【分析】
分别求出不等式组中两不等式的解集,表示在数轴上,找出两解集的公共部分,即可得到原不等式组的解
集.【详解】解:由题意知:
解不等式 :去分母得: ,
移项得: ,
系数化为1得: ,
解不等式 ,得 ,
在数轴上表示不等式 的解集如图:
不等式组的解集为 .
【点睛】此题考查了一元一次不等式组的解法,以及在数轴上表示不等式组的解集,其中不等式组的解集
取法为:同大取大,同小取小,大大小小无解,大小小大取中间.
19.先化简,再求值: ,其中 .
【答案】 ,1
【解析】
【分析】
根据分式的加减乘除运算法则进行运算即可化简,最后将 代入求解即可.
【详解】解:原式当 时代入,
原式 .
故答案为:1.
【点睛】本题考查分式的加减乘除运算法则及化简求值,先乘除,再加减,有括号先算括号内的,熟练掌
握运算法则及运算顺序是解决此类题的关键.
20.如图,在 中, 的平分线 交 于点 .求 的
长?
【答案】6
【解析】
【分析】
由 求出∠A=30°,进而得出∠ABC=60°,由BD是∠ABC的平分线得出∠CBD=30°,进而求出BC
的长,最后用sin∠A即可求出AB的长.
【详解】解:在 中,
是 的平分线,又
,
在 中, ,
.
故答案为: .
【点睛】本题考查了用三角函数解直角三角形,熟练掌握三角函数的定义及特殊角的三角函数是解决此类
题的关键.
21.如图,点 是正方形, 的中心.
(1)用直尺和圆规在正方形内部作一点 (异于点 ),使得 (保留作图痕迹,不写作法)
(2)连接 求证: .
【答案】(1)见解析;(2)见解析
【解析】
【分析】
(1)作BC的垂直平分线即可求解;
(2)根据题意证明 即可求解.
【详解】 如图所示,点 即为所求.连接
由 得:
是正方形 中心,
在 和 中,
.
【点睛】此题主要考查正方形的性质与证明,解题的关键是熟知正方形的性质、垂直平分线的作图及全等
三角形的判定与性质.
22.在某次疫情发生后,根据疾控部门发布的统计数据,绘制出如下统计图:图 为 地区累计确诊人数
的条形统计图,图 为 地区新增确诊人数的折线统计图.(1)根据图 中的数据, 地区星期三累计确诊人数为 ,新增确诊人数为 ;
(2)已知 地区星期一新增确诊人数为 人,在图 中画出表示 地区新增确诊人数的折线统计图.
(3)你对这两个地区的疫情做怎样的分析,推断?
【答案】(1)41,13;(2)见解析;(3)见解析(答案不唯一)
【解析】
【分析】
(1)根据图①的条形统计图即可求解;
(2)根据图 中的数据即可画出折线统计图;
(3)根据折线统计图,言之有理即可.
【详解】(1) 地区星期三累计确诊人数为41;新增确诊人数为41-28=13,
故答案为:41;13;
如图所示:
地区累计确诊人数可能会持续增加, 地区新增人数有减少趋势,疫情控制情况较好(答案不唯一).
【点睛】此题主要考查统计图的应用,解题的关键是根据题意作出折线统计图.
23.生活在数字时代的我们,很多场合用二维码(如图 )来表示不同的信息,类似地,可通过在矩形网格中,对每一个小方格涂加色或不涂色所得的图形来表示不同的信息,例如:网格中只有一个小方格,如图
,通过涂器色或不涂色可表示两个不同的信息.
(1)用树状图或列表格的方法,求图 可表示不同信息的总个数:(图中标号 表示两个不同位置的小方
格,下同)
(2)图 为 的网格图.它可表示不同信息的总个数为 ;
(3)某校需要给每位师生制作一张“校园出入证”,准备在证件的右下角采用 的网格图来表示各人身份
信息,若该校师生共 人,则 的最小值为 ;
【答案】(1)见解析;(2)16;(3)3
【解析】
【分析】
(1)根据题意画出树状图即可求解;
(2)根据题意画出树状图即可求解;
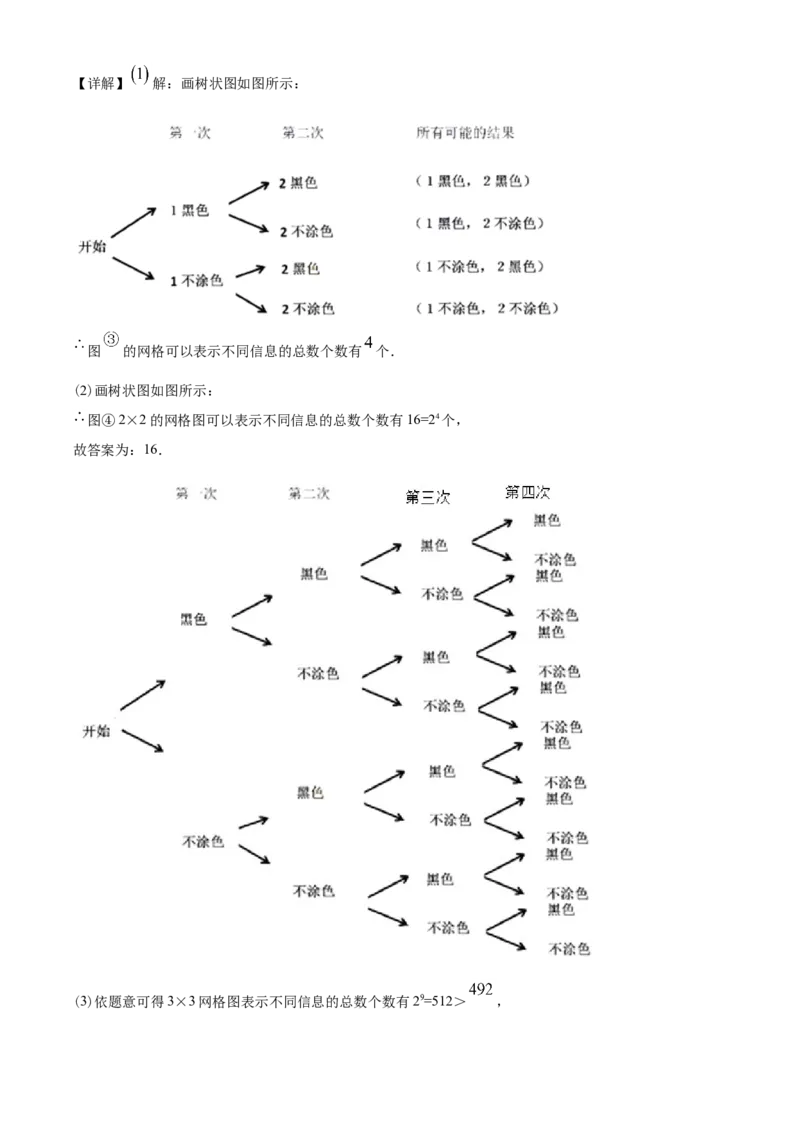
(3)根据(1)(2)得到规律即可求出n的值.【详解】 解:画树状图如图所示:
图 的网格可以表示不同信息的总数个数有 个.
(2)画树状图如图所示:
图④2×2的网格图可以表示不同信息的总数个数有16=24个,
故答案为:16.
(3)依题意可得3×3网格图表示不同信息的总数个数有29=512> ,故则 的最小值为3,
故答案为:3.
【点睛】此题主要考查画树状图与找规律,解题的关键是根据题意画出树状图.
24.如图, 是 的外接圆, 是 的直径, .
(1)求证: 是 的切线;
(2)若 ,垂足为 交 与点;求证: 是等腰三角形.
【答案】(1)见解析;(2)见解析
【解析】
【分析】
(1)连接 OC,由 AB 是圆 O 的直径得到∠BCA=90°,进一步得到∠A+∠B=90°,再根据已知条件
,且∠A=∠ACO即可证明∠OCD=90°进而求解;
(2)证明 ,再由DE⊥AB,得到∠A+∠AFE=90°,进而得到∠DCA=∠AFE=∠DFC,得到
DC=DF,进而得到△DFC为等腰三角形.
【详解】解:(1)证明:连接 ,为圆 的直径,
又
又 点 在圆 上,
是 的切线.
(2)又
是等腰三角形.
【点睛】本题考查了圆的切线的判定定理,圆周角定理,等腰三角形的性质和判定等,熟练掌握性质或定
理是解决此类题的关键.
25.若二次函数 的图像与 轴有两个交点 ,且经过点
过点 的直线 与 轴交于点 与该函数的图像交于点 (异于点 ).满足 是等腰直角
三角形,记 的面积为 的面积为 ,且 .
(1)抛物线的开口方向 (填“上”或“下”);
(2)求直线 相应的函数表达式;
(3)求该二次函数的表达式.
【答案】(1)上;(2) ;(3)
【解析】
【分析】
(1)由抛物线经过点M、N、A点即可确定开口向上;(2)根据 是等腰直角三角形分三种情况讨论,只能是 ,此时
,由此算出C点坐标,进而求解;
(3)过B点作BH⊥x轴,由 得到 ,由OA的长求出BH的长,再将B点纵坐标代入直
线l中求出B点坐标,最后将A、B、N三点坐标代入二次函数解析式中求解即可.
【详解】解:(1)∵抛物线经过点M、N、A,且M、N点在x轴正半轴上,A点在y轴正半轴上,
∴抛物线开口向上,
故答案为:上.
(2)①若 ,
则 与 重合,直线 与二次函数图像交于 点
∵直线与该函数的图像交于点 (异于点 )
∴不合符题意,舍去;
②若 ,则 在 轴下方,
∵点 在 轴上,
∴不合符题意,舍去;
③若
则
设直线
将 代入:
,解得
直线 .故答案为: .
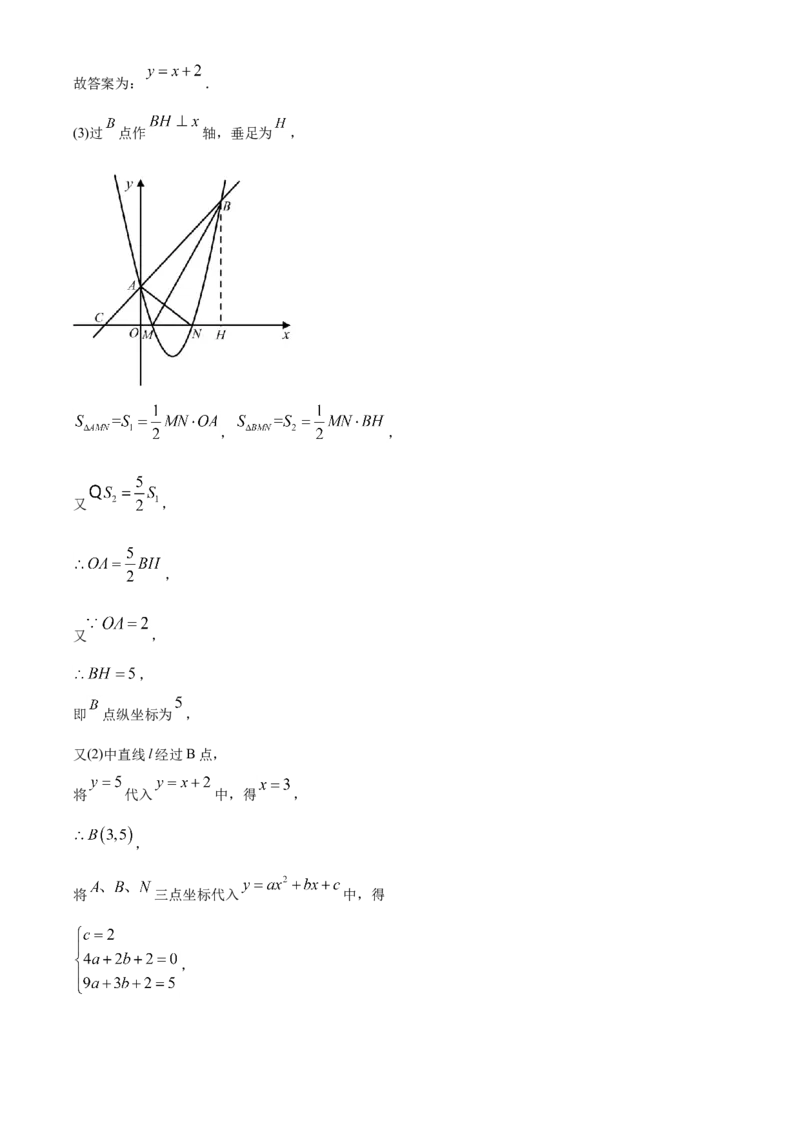
(3)过 点作 轴,垂足为 ,
, ,
又 ,
,
又 ,
,
即 点纵坐标为 ,
又(2)中直线l经过B点,
将 代入 中,得 ,
,
将 三点坐标代入 中,得
,解得 ,
抛物线解析式为 .
故答案为: .
【点睛】本题考查了二次函数解析式的求法,二次函数和一次函数的交点坐标,等腰直角三角形分类讨论
的思想,熟练掌握二次函数的图形及性质是解决此类题的关键.
26.木门常常需要雕刻美丽的图案.
(1)图①为某矩形木门示意图,其中 长为 厘米, 长为 厘米,阴影部分是边长为 厘米的
正方形雕刻模具,刻刀的位置在模具的中心点 处,在雕刻时始终保持模具的一边紧贴木门的一边,所刻
图案如虚线所示,求图案的周长;
(2)如图 ,对于 中的木门,当模具换成边长为 厘米的等边三角形时,刻刀的位置仍在模具的
中心点 处,雕刻时也始终保持模具的一边紧贴本门的一边,使模具进行滑动雕刻.但当模具的一个顶点
与木门的一个顶点重合时,需将模具绕着重合点进行旋转雕刻,直到模具的另一边与木门的另一边重合.
再滑动模具进行雕刻,如此雕刻一周,请在图 中画出雕刻所得图案的草图,并求其周长.【答案】(1) ;(2)雕刻所得图案的草图见解析,图案的周长为
【解析】
【分析】
(1)过点 作 求出PE,进而求得该图案的长和宽,利用长方形的周长公式即可解答;
(2)如图,过P作PQ⊥CD于Q,连接PG,先利用等边三角形的性质求出PQ、PG及∠PGE,当移动到点
时,求得旋转角和点P旋转的路径长,用同样的方法继续移动,即可画出图案的草图,再结合图形可求
得所得图案的周长.
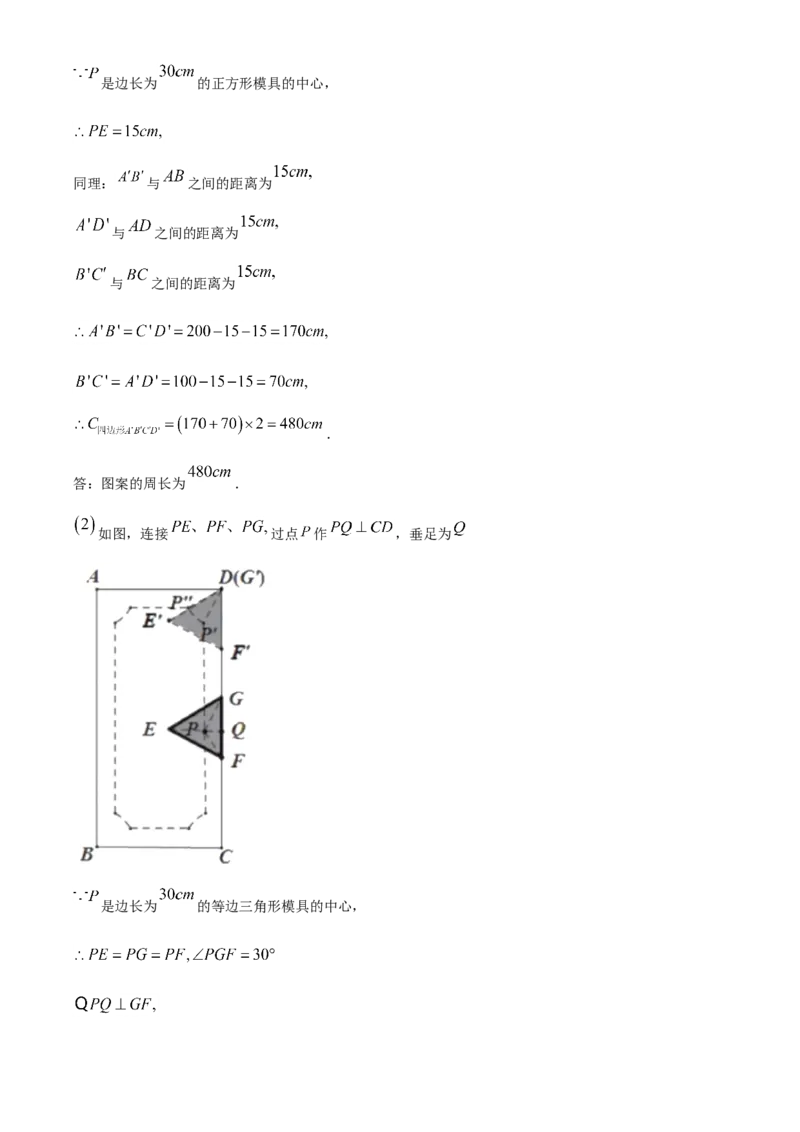
【详解】 如图,过点 作 垂足为是边长为 的正方形模具的中心,
同理: 与 之间的距离为
与 之间的距离为
与 之间的距离为
.
答:图案的周长为 .
如图,连接 过点 作 ,垂足为
是边长为 的等边三角形模具的中心,.
当三角形 向上平移至点 与点 重合时,
由题意可得: 绕点 顺时针旋转
使得 与 边重合
绕点 顺时针旋转 至
.
同理可得其余三个角均为弧长为 的圆弧,
图中的虚线即为所画的草图,
∴
.
答:雕刻所得图案的草图的周长为 .
【点睛】本题考查了图形的平移与旋转、等边三角形的性质、解含30º角的直角三角形、图形的周长等知
识,解答的关键是熟练掌握图形平移和旋转过程中的变化特征,结合基本图形的性质进行推理、探究、发
现和计算.
27.以下虚线框中为一个合作学习小组在一次数学实验中的过程记录,请阅读后完成虚线框下方的问题
.
(1)在 中, ,在探究三边关系时,通过画图,度量和计算,收集到,组数据
如下表:(单位:厘米)(2)根据学习函数的经验,选取上表中 和 的数据进行分析;
设 ,以 为坐标,在图 所示的坐标系中描出对应的点;
连线;
观察思考
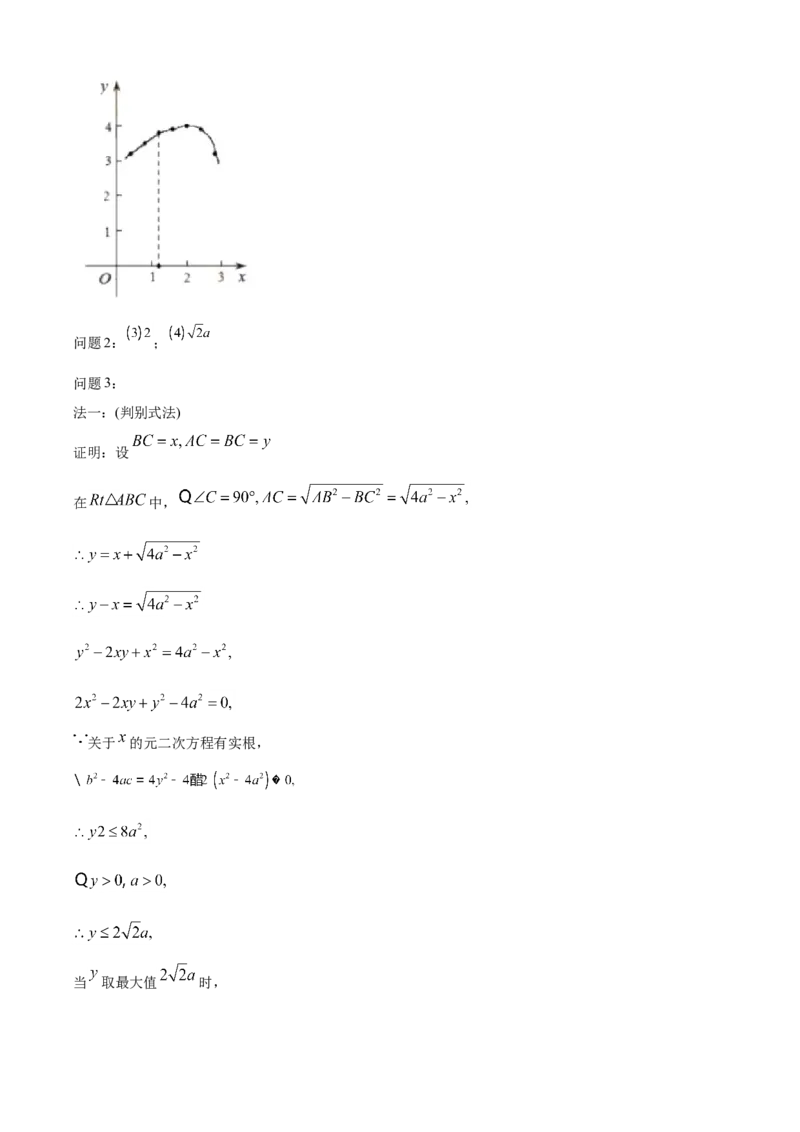
(3)结合表中的数据以及所面的图像,猜想.当 时, 最大;
(4)进一步C猜想:若 中, ,斜边 为常数, ),则
时, 最大.
推理证明
(5)对(4)中的猜想进行证明.
问题1.在图 中完善 的描点过程,并依次连线;
问题2.补全观察思考中的两个猜想: _______ _______
问题3.证明上述 中的猜想:问题4.图 中折线 是一个感光元件的截面设计草图,其中点 间的距离是 厘米,
厘米, 平行光线从 区域射入, 线段 为
感光区城,当 的长度为多少时,感光区域长度之和最大,并求出最大值.
【答案】问题1:见解析;问题2:2, ;问题3:见解析;问题4:当 时,感光区域长
度之和 最大
为
【解析】
【分析】
问题1:根据(1)中的表格数据,描点连线,作出图形即可;
问题2:根据(1)中的表格数据,可以得知当 2时, 最大;设 ,则
,可得 ,有 ,可得出 ;
问题3:可用两种方法证明,方法一:(判别式法)设 ,则 ,可得
,有 ,可得出 ;方法二:(基本不等式),设
,得 ,可得 ,根据当 时,等式成立有
,可得出;
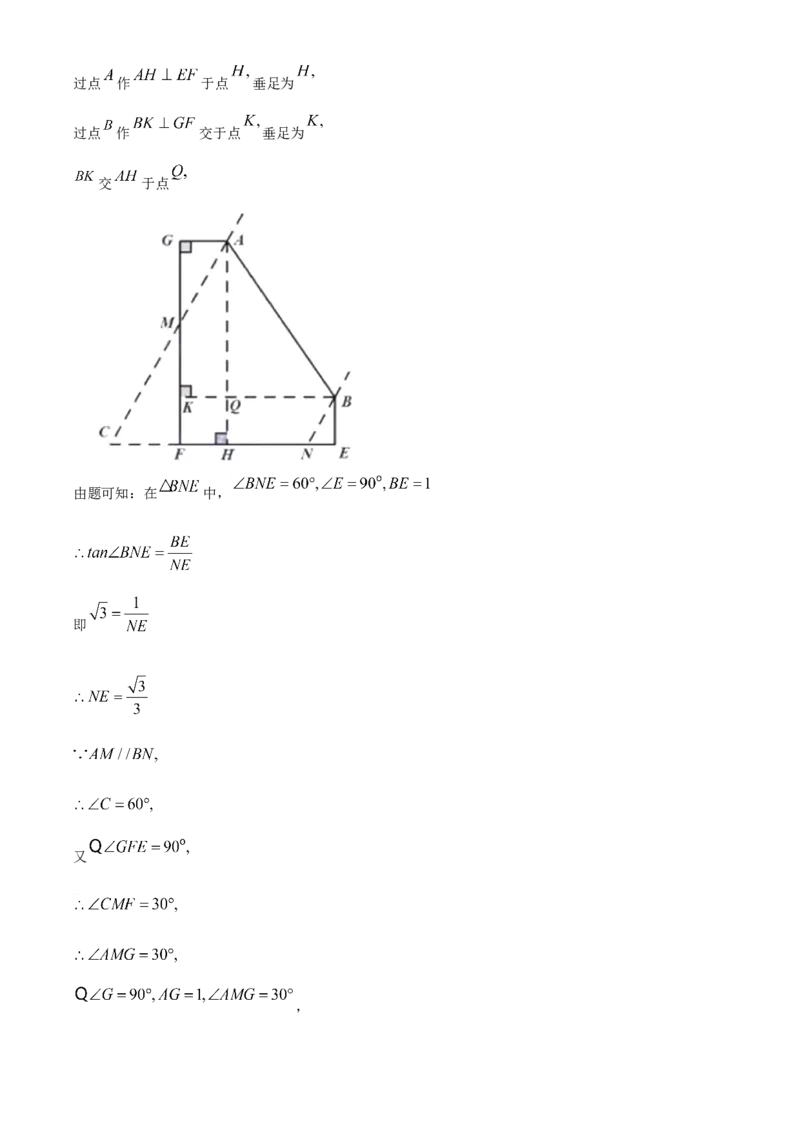
问题4:方法一:延长 交 于点 ,过点 作 于点 ,垂足为 ,过点 作
交于点 ,垂足为 , 交 于点 ,由题可知:在 中, ,
得 ,根据 ,有 ,得 ,易证四边形
为矩形,四边形 为矩形,根据 可得
,由问题3可知,当 时, 最大,则有
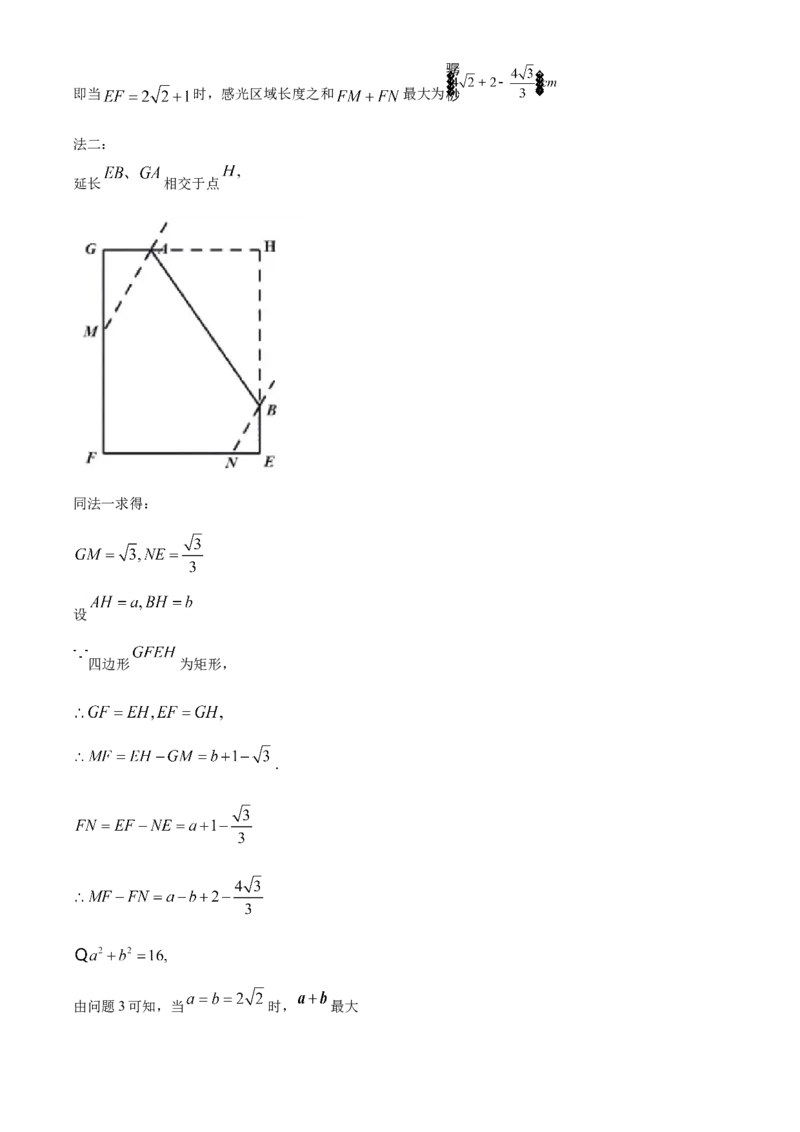
时, 最大为 ;方法二:
延长 相交于点 同法一求得: ,根据四边形 为矩形,有
, ,得到 ,由问题3可
知,当 时, 最大
则可得 时 最大为 .
【详解】问题1:图问题2: ;
问题3:
法一:(判别式法)
证明:设
在 中,
关于 的元二次方程有实根,
当 取最大值 时,当 时, 有最大值.
法二:(基本不等式)
设
在 中,
.
当 时,等式成立
.
,
当 时, 有最大值.
问题4:
法一:延长 交 于点过点 作 于点 垂足为
过点 作 交于点 垂足为
交 于点
由题可知:在 中,
即
又
,在 中,
,
即
四边形 为矩形
,
四边形 为矩形,
在 中, .
由问题3可知,当 时, 最大
时, 最大为即当 时,感光区域长度之和 最大为
法二:
延长 相交于点
同法一求得:
设
四边形 为矩形,
.
由问题3可知,当 时, 最大时 最大为
即当 时,感光区域长度之和 最大为 .
【点睛】本题考查了一元二次方程,二次函数,不等式,解直角三角形,三角函数,矩形的性质等知识点,
熟悉相关性质是解题的关键.